燃气-蒸汽弹射喷水多相汽化计算及影响分析

惠卫华，杨玉磊，马艳杰,于城博，李 猛

(1 西北工业大学固体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710072；2 西安近代化学研究所，西安 710065)

0 引言

弹射是依靠外加动力弹射出筒后导弹发动机点火发射的过程。弹射技术已经日趋成熟，凭借装置简单、机动性强、速度快等优点被各国广泛应用于战略技术导弹的发射、鱼雷发射、地下井发射、陆基机动发射等方面。其中燃气-蒸汽弹射以其燃气-蒸汽温度低、能量利用充分、对导弹烧蚀轻、防热简单、压力变化平稳等优点而备受青睐[1]。

Edquist[2]首先建立了燃气-蒸汽弹射发射过程内弹道数学模型。赵世平[3]研制出了一套用于预估燃气-蒸汽弹射内弹道性能的程序。随着计算流体力学的发展，研究人员开始采用数值仿真技术研究燃气-蒸汽弹射内流场。肖虎斌[4]采用雾化理论研究了冷却水汽化过程。刘伯伟[5]利用真实气体模型模拟集中注水式燃气-蒸汽弹射过程中水蒸汽的状态变化。胡晓磊[6]研究了喷水孔数量、喷水孔直径分别对燃气-蒸汽弹射内弹道的影响，但没有保证注水流量相同。文中采用Mixture多相流模型和汽化模型结合RNGk-ε湍流模型[7]，研究在相同流量条件下，改变孔的数量，不同喷水孔径对汽化速度以及对流场的影响。

1 物理模型和计算方法

1.1 物理模型

燃气-蒸汽弹射系统弯管前几何模型如图1所示，主要包括燃气发生器、一级喷管、导流管、分流管、二级喷管、水室、喷水孔和连接管。燃气经过一级喷管部分进入二级喷管，剩余部分经过分流管进入水室挤压冷却水进入二级喷管与燃气混合。

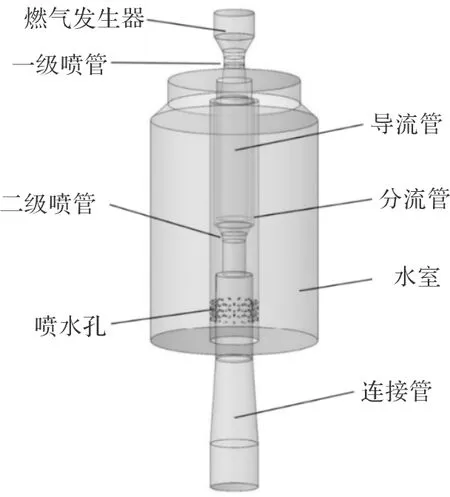
图1 燃气-蒸汽弹射仿真几何模型

注水流量公式[9]为：

(1)

式中：μ为喷水孔流量系数;N为喷水孔数量;S为水孔截面积;ρ1为水密度;λ为喷水压差系数;Pc为燃烧室压力。可知注水流量由喷水孔数量、喷水孔截面积和压差系数决定，对于某燃气-蒸汽弹射系统，若喷水孔总截面积NS相同，则注水流量相同。

1.2 控制方程

燃气-蒸汽弹射流场数值模拟采用了欧拉-欧拉法描述，引入体积分数的概念，假设在空间和时间上连续，不同的相占据不同的体积分数，但其总和为1。推导出每一相控制方程在结构上是相似的。

1.2.1 连续方程

(2)

式中：ρm为混合密度，并且满足

ρm=α1ρ1+αvρv

(3)

vm是质量平均速度，并且满足

vm=(α1ρ1v1+αvρvvv)/ρm

(4)

下标1代表液相，v代表气相；α1，αv分别为液相和气相的体积分数，并且α1+αv=1；ρ1、ρv分别为液相和气相的密度；v1、vv分别为液相和气相的速度。

1.2.2 动量方程

(5)

式中：μm为混合粘度，并且满足

μm=α1μ1+αvμv

(6)

vdr,1、vdr,v分别为液相和气相的迁移速度，vdr,1=v1-vm，vdr,v=vv-vm。

1.2.3 能量方程

(7)

式中：

(8)

(9)

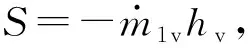
(10)

液态水汽化公式为：

(11)

水蒸气凝结公式为：

(12)

式中：λ为时间松弛因子，取λ=0.1；T为混合温度；Tsat为液态水的饱和温度。

1.3 网格划分和边界条件

模型为周期性旋转模型，为了节约计算资源节省计算时间，仅对1/7的模型进行网格划分，建立旋转周期网格，如图 2所示。网格数：18万，节点数：20万。

图2 1/7网格模型

入口条件：燃气发生器入口采用质量入口条件，将试验测得的燃气发生器工作压力结合几何尺寸代入质量流率公式：

qm=PcAt/c*

(13)

得到入口质量流率曲线如图 3所示。采用线性差值方法编写UDF实现一级喷管流量的输入。

出口条件：连接管出口采用压力出口条件，设置为与筒内初始压力相同。由于弯管前建压迅速，很快达到声速，下游扰动无法传播到上游，因此弯管前模型不受下游发射筒压力波动的影响，出口条件选择压力出口条件较为合理。

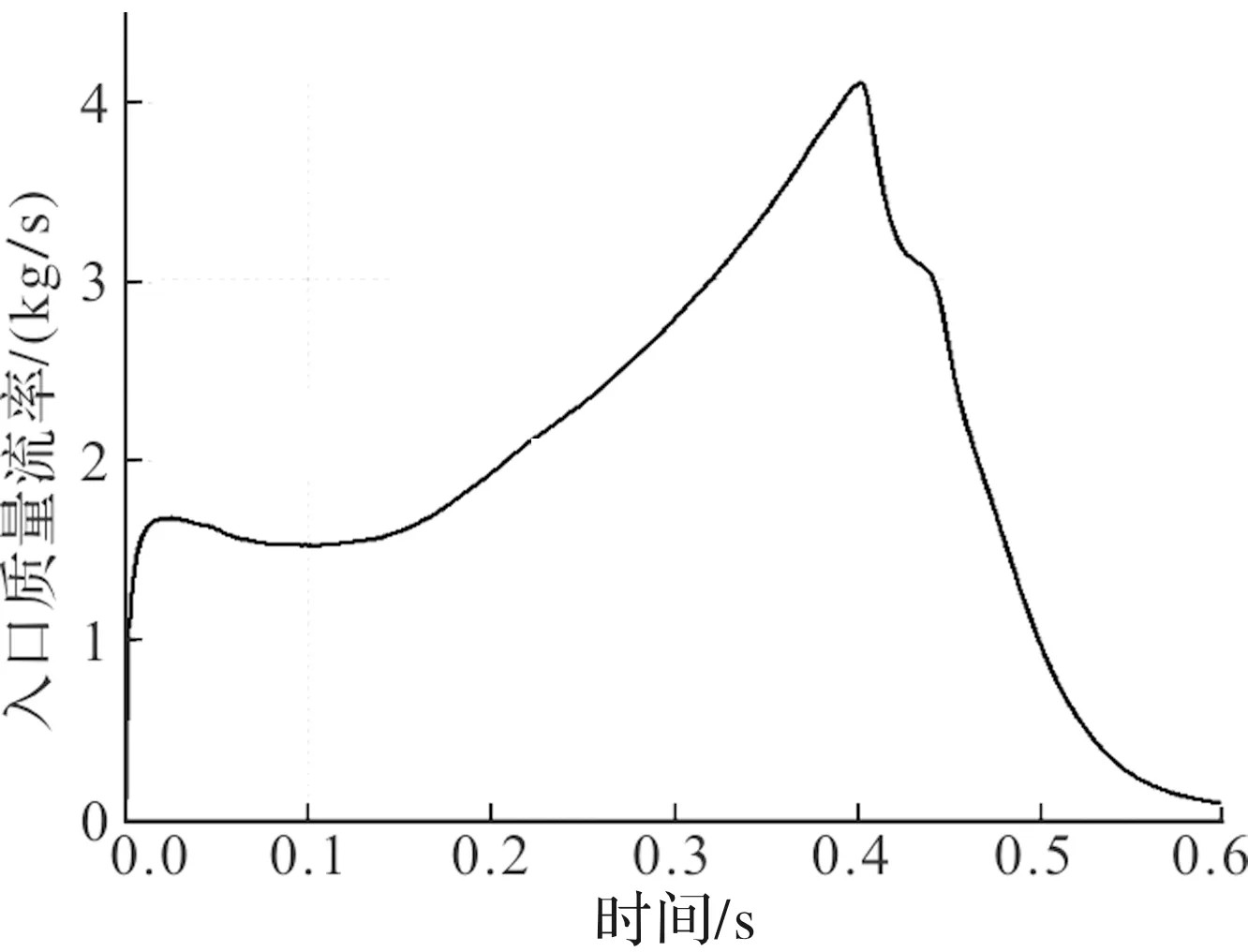
图3 一级喷管入口质量流率曲线

周期性条件：在划分网格时设置旋转轴为模型的中心轴，周期数为7，设置对应的周期性节点，保证周期边界上网格节点一一对应。

2 数值方法校验

为检验数值方法的可靠性，先对其进行验证，应用文中建立的数值模型对图 2所示56个注水口未加预注水的燃气-蒸汽弹射1/7模型进行数值仿真，然后与试验结果对比。结果如图 4所示，二者趋势一致，最大相对误差不超过14%，在可接受的范围内，说明建立的数值方法可以用于该燃气-蒸汽弹射模型仿真计算。

图4 注水口出口仿真与试验压力对比

3 结果分析

喷水孔采用圆柱形结构，如图 5所示，保证喷水孔总截面积相同的前提下设置两种不同的方案，方案一：4排共56个孔，内径2 mm；方案二：2排共14个孔，内径4 mm。

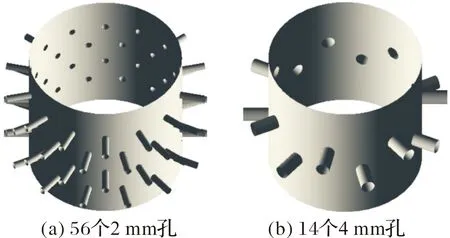
图5 喷水孔结构示意图

3.1 压力分析

对这两种不同方案分别进行流场分析计算。

两种方案相同时刻压力分布近乎一致，高压燃气由一级喷管进入加速膨胀压力降低，在导流管内压力回升，部分高压燃气经分流管进入水室对水室增压，主流燃气经二级喷管进一步加速膨胀，压力再一次下降，在连接管内有明显的膨胀波。随着入口压力的提高，各部位压力均有提高。

连接管出口平均压力曲线如图 6所示，可以看到压力曲线初始时有压力峰，这是由于没有加预注水造成的，此时两条曲线十分相近，之后受连续注水影响压力下降，然后平稳上升，方案二略低于方案一，压力相差约0.02 MPa。

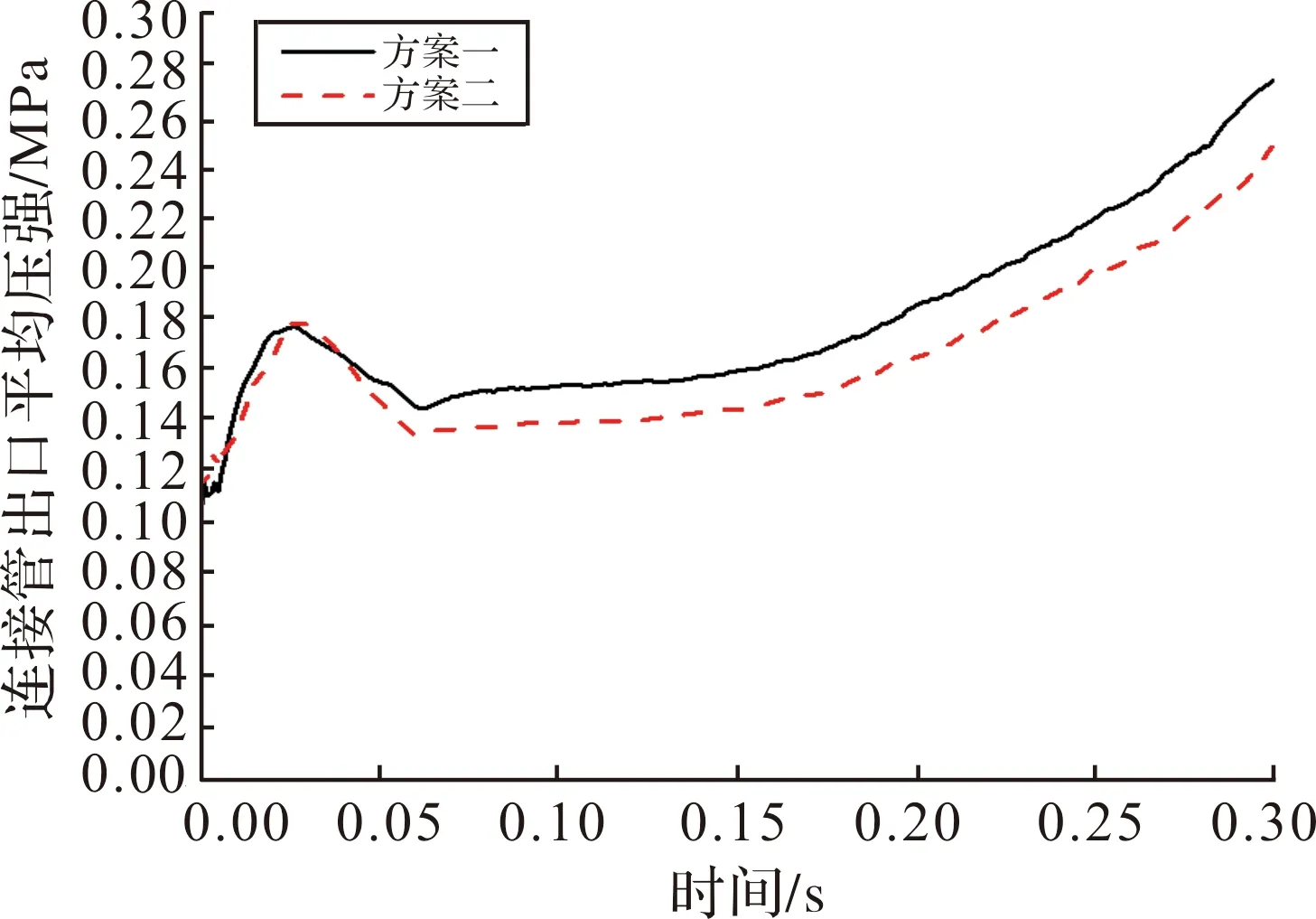
图6 连接管出口平均压力曲线

3.2 温度分析

如图7所示，两种方案温度分布类似，燃气流经一级喷管温度略有下降，之后在导流管内回升，部分高温燃气经分流管进入水室，主流燃气经二级喷管后温度大幅下降。在喷水孔后温度出现清晰的分界，中心区域温度显著高于周围，且越接近中心温度越高，随着燃气接近连接管出口位置，中心区域温度逐渐趋于均匀。

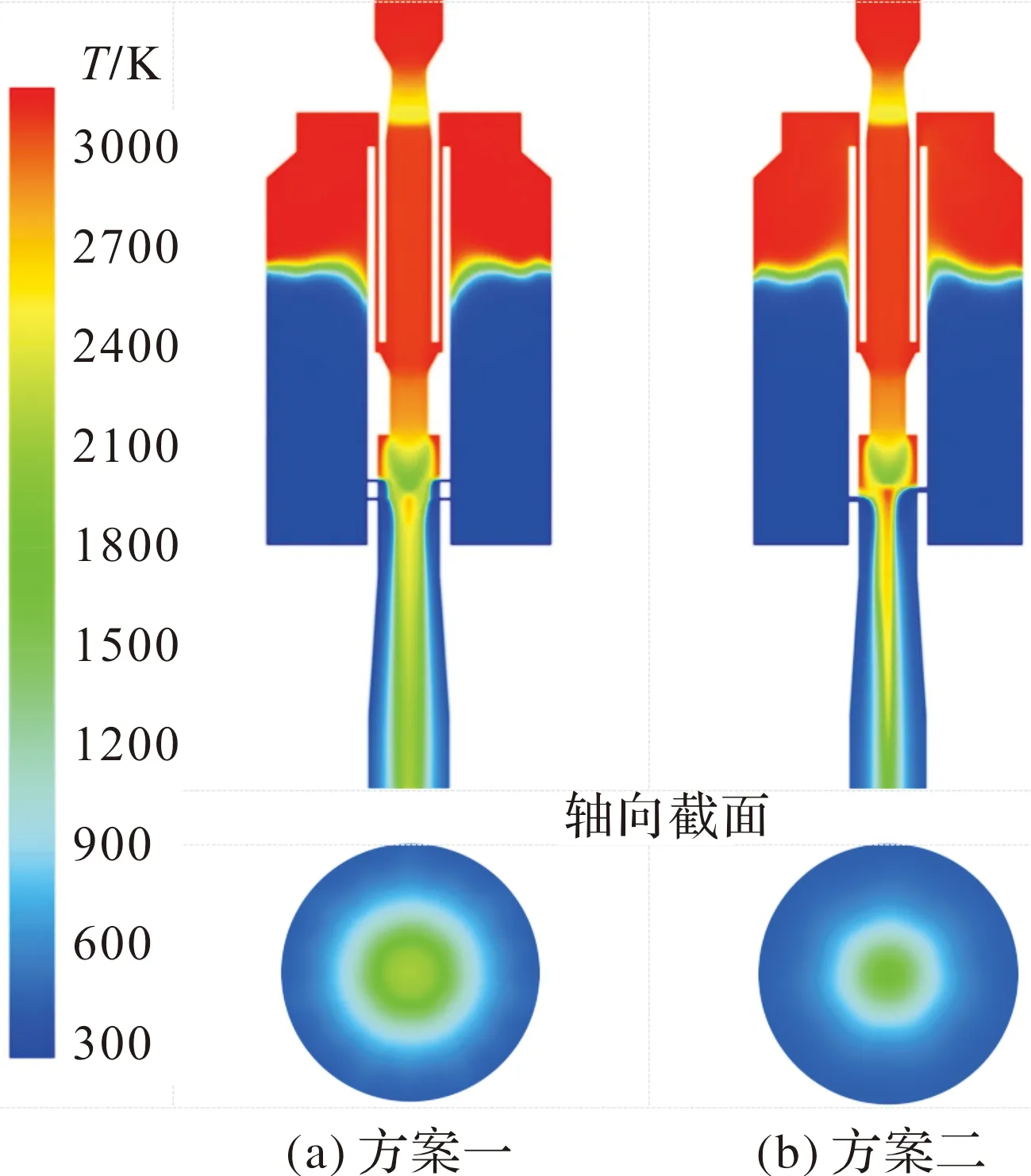
图7 两种方案0.3 s时刻温度云图

喷水孔前后壁面温差达2 500 K。喷水孔后连接管内的温度分布出现差异，方案一中心轴线上温度最高2 700 K，方案二中心轴线上温度最高2 900 K；方案一出口热通量，方案二出口热通量；以1 000 K作为中心高温区与周围低温区的分界面，方案一高温区直径约为连接管直径的1/2，方案二高温区直径约为连接管直径的1/3。即方案二注水口处温度虽高，但高温区范围明显小于方案一，连接管出口热通量更高，说明方案一经过冷却水汽化参混使得热量分布更均匀且热量更低。

3.3 体积分数分析

如图8所示，液相从喷水孔进入连接管后迅速蒸发，液相体积分数快速下降，随着流动蒸发逐渐完全，未蒸发的液相贴着壁面流动。方案一相比方案二体积分数下降更快，液相所占体积更少，连接段出口位置体积分数更低，说明方案一液相蒸发更快。

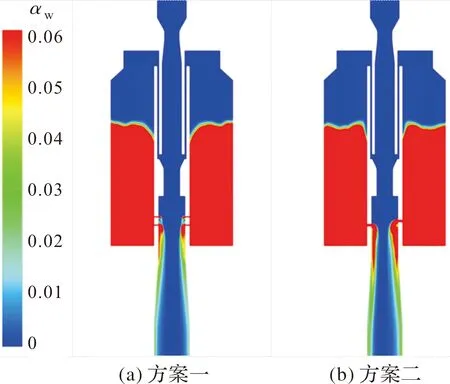
图8 两种方案0.3 s时刻液相体积分数云图

3.4 质量转化率分析

水蒸发汽化过程主要发生在水室气液界面处和喷水口出口后的连接管内，由于在水室内蒸发汽化的水蒸气无法进入连接管及之后的发射筒内，对流场影响不明显，所以在此不做考虑。结合液相体积分数对比图可知，液相从喷水口喷出后在压力的作用下沿着壁面流动，汽化发生在液相表面，方案一较为接近壁面，而方案二更靠近中心位置。随着流动的继续，逐渐贴近壁面，蒸发率和蒸发范围也逐渐扩大。总体而言，从质量转化率对比图 9和图 10可以看出，在连接管出口位置，虽然方案一出口最大蒸发率普遍高于方案二，但总转化率低于方案二，随着时间增长差异越明显。结合前面对液相体积分数的分析可知，这是因为液相从喷水口流出后方案一相比方案二蒸发较快，在出口位置接近蒸发完全，体积分数比方案二低，从而出口位置方案二的质量转化率更高。

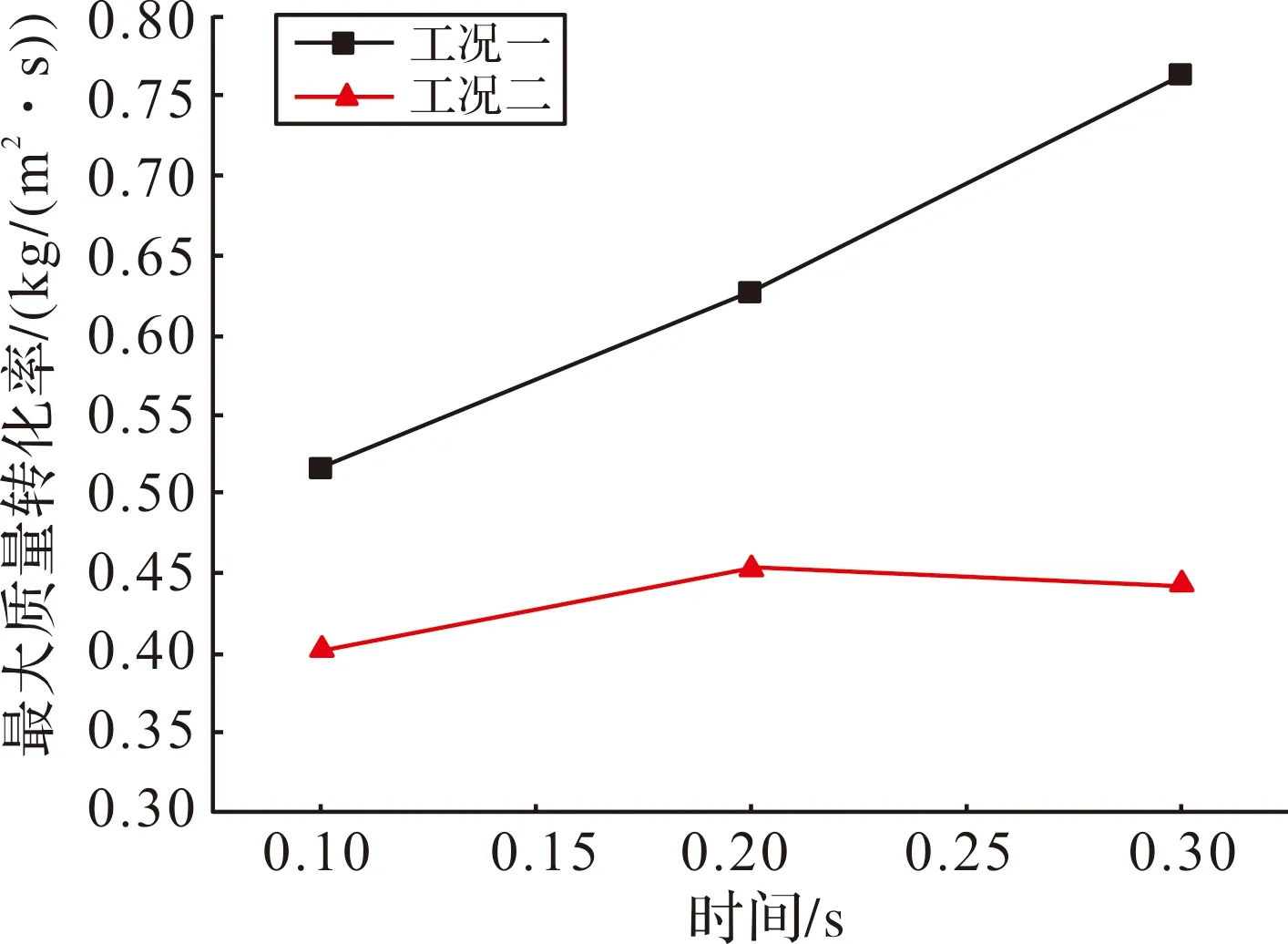
图9 连接管出口最大质量转化率曲线

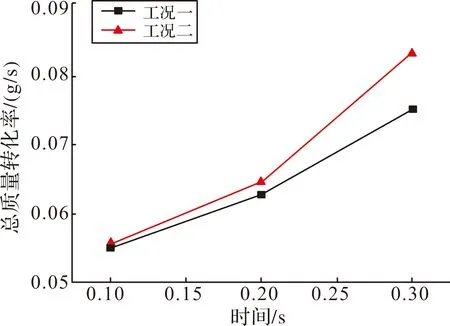
图10 连接管出口总质量转化率曲线

4 结论

通过研究，所得主要结论如下：

1)燃气-蒸汽弹射过程中，冷却水的汽化主要发生在连接管内，汽化过程主要发生在喷水孔出口与燃气接触的液相表面。

2)相同总喷水孔面积，即相同注水流量条件下，孔数量越多直径越小，冷却水对燃气降温作用越明显，细密的孔更有利于冷却水快速蒸发汽化。

3)相同喷水孔总面积，足够长的连接管可使得冷却水充分蒸发，则喷水孔的细密程度不会对压力有太大影响。

4)相同总喷水孔面积，孔数量越多直径越小，连接管出口热量更小，而压力更高，则进入弹射筒的燃气做功能力更强，且降低了发射筒及导弹的热防护要求。