车门限位器主臂曲线方程及力学性能变化规律研究

潘毓滨 代世磊 张敏

（1.广汽蔚来新能源汽车科技有限公司，广州 511434；2.申雅密封件（广州）有限公司，广州 511434）

主题词：车门限位器 限位臂曲线 解析方程 迭代法 设计优化 力学性能

1 前言

随着汽车的大量普及，消费者越来越注重用户体验。车门开闭感（用户开关车门的体验感）作为潜在用户考察车辆时最先产生的操作体验，逐渐成为汽车生产厂商的重点研究内容[1-5]。车门开闭感的影响因素众多，主要包括车门总成、限位器、铰链、密封条、门锁和外开手柄等。限位器不仅为车门提供保持功能，而且影响着车门的关门能量和开、关车门时的操作手感，在提升车门开闭感时需要重点研究[6-14]。限位器主臂曲线对车门开闭感和空间布置都存在很大影响，其设计过程贯穿车型前期概念设计至后期详细设计多个阶段，是限位器设计的重点内容[15-16]。目前，一般采用迭代作图法[17-18]，或者基于迭代作图法原理编程的方法[19]设计限位器主臂曲线。但是传统的迭代作图法精度较差，而编程的方法门槛较高，不便于广泛采用，因此，亟需寻找一种便于使用且具有较高精度的方法。限位臂曲线的设计往往不是一蹴而就的，一般需要经过反复优化，才能得到形状、尺寸和力学性能均理想的结果。目前，行业内还没有关于限位臂曲线及力学性能变化规律的系统性研究成果[20-21]，限位臂的优化过程效率较低。在研究限位臂曲线及力学性能变化规律时，如何选定分析参数非常重要，分析角度、坐标系和布置方案不同，可以定义不同的分析参数。本文在大量设计布置经验基础上，结合理论分析分别研究不同设计参数对限位臂曲线和力学性能的影响规律。

2 限位器主臂曲线解析方程求解

2.1 限位臂-车门运动分析模型建立

如图1 所示，限位臂与限位盒中的滑块在A0处啮合，A为曲线中的某一点。车门开启角度为θ时，限位臂曲线上A点运动到A′处，同时，限位盒（固定在车门上）上A0也运动到A′处，此时，限位臂与限位盒中的滑块在A′处啮合。

图1 限位器示意

如图2所示，过A′点且垂直于铰链轴线的平面与铰链轴线、限位器轴线分别相交于O、O′，记该平面为OO′A′。设θ为OA′与OA0的夹角，代表车门开启角度，在初始状态位置，θ=0°；设ξ为OA0与OO′的夹角；设φA、φA′分别为O′A、O′A′与OO′的夹角。车门开启角度为θ时，限位臂对应转过的角度为φ=φA′-φA。需要说明的是，在任意状态下，限位臂中心线上每个点对应的φA和φA′均不一定相同，但转过的角度φ却是相等的。

图2 限位器运动分析示意

记车门开启角度为θ时，限位臂中心线在A′点处的切线单位向量为n，法向单位向量为m，n和m的方向均指向车身外侧。n与A′O、A′O′以及O′O的夹角分别为α、β、δ，车门开启过程中α始终为定值，一般地，0＜α＜π/2，且有δ=θ+ξ+α。记限位器盒在A′点处的运动速度为v1，车门开启角速度为ω1，限位臂在A′点处的运动速度为v2，限位臂运动角速度为ω2。

2.2 限位器主臂曲线解析方程推导

在平面OO′A′上，以OO′为纵轴，建立平面坐标系x′Oy′，本文以x′Oy′为基准坐标系进行推导。

记O=(0,0)、O′=(0,l)、A=(x,y)、A′=(x′,y′)，令r1=OA=(x1,y1)，r2=O′A=(x2,y2)，r1、r2的模长分别为r1、r2，则有：

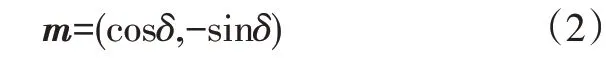
由于限位块与限位臂在平面OO′A′上沿垂直于限位臂中心线方向上是相对静止的，即v1与v2在m方向分量相等，故有：

由于m、v1与v2都是平面向量，根据向量的运算关系，可得：

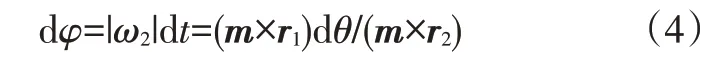
所以有：

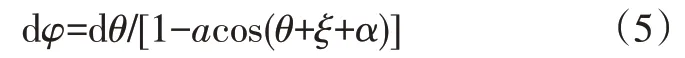
式中，a=l/(r1cosα)，且1-acos(θ+ξ+α)＞0。

可以看出，φ是关于θ的函数，通过积分运算化简可得：

3 迭代法的验证及优化

3.1 迭代法验证

工程上，普遍采用迭代作图法在软件上设计限位臂曲线。将车门最大开启角度均分成若干等份步长Δθ，逐步求解每步对应的限位臂曲线上的位置，从而近似拟合出整条曲线。迭代作图法可分为前迭代法和后迭代法，如图3 和图4 所示，为限位臂曲线运动到处的切线。Si为直线与以O′为圆心且过点的圆的交点，车门从运动到过程中，前、后迭代法中限位臂分别对应转过O′Si、∠Si-1O′。前迭代法和后迭代法原理相同，通过设计算法编写程序[19]，便可求解出对应曲线。

图3 前迭代法

图4 后迭代法

分别采用限位臂曲线方程和迭代法求解限位臂曲线，参数设置如表1所示。前、后迭代法分别采用1°、5°和10°3个步长进行计算，求解结果如图5所示。由图5可知：前迭代法与后迭代法求解出的曲线均分列在理论曲线（通过曲线方程求得）两侧；在步长较大时，前、后迭代法求得的曲线差别较大；步长越小，2 种迭代法求得的曲线越接近理论曲线；当步长为1°时，2 条曲线较为接近，但仍然存在肉眼可见的差异。

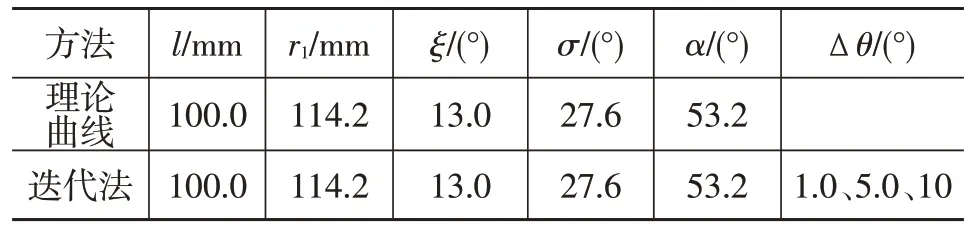
表1 采用解析方程和迭代法求解限位臂曲线的相关参数

对前、后迭代法的研究表明，前、后迭代法只有在步长小于1°时，才能求得比较接近理论曲线的结果，用手工绘图的方式实现如此小的步长几乎是不可能的。采用同样步长，分别用前、后迭代法求得A11、A21、A31、……、AN1和A12、A22、A32、……、AN2，如图6所示。分别取A11和A12的中点A1、A21和A22的中点A2、……、AN1和AN2的中点AN，将A0、A1、A2、……、AN连接成曲线，得到平均迭代法曲线。

图5 前、后迭代法与理论曲线结果对比

3.2 平均迭代法

采用平均迭代法分别按步长为1°、5°和10°，求得相应曲线如图7所示。从图7中可以看到，以10°步长求得的平均迭代法曲线比以1°步长求得的前、后迭代法曲线都更加接近理论曲线，以1°步长求得的平均迭代法曲线与理论曲线几乎完全贴合。显然，采用平均迭代法，采用较大的步长、较少的步数，即可获得精度较高的限位臂近似曲线。

4 布置参数对限位臂曲线的影响规律分析

在车门及附件系统的前期布置过程中，需要保证限位器运动包络与车门密封条、车门玻璃、玻璃导轨、车门内板等零件之间有足够的运动间隙，如图8所示。

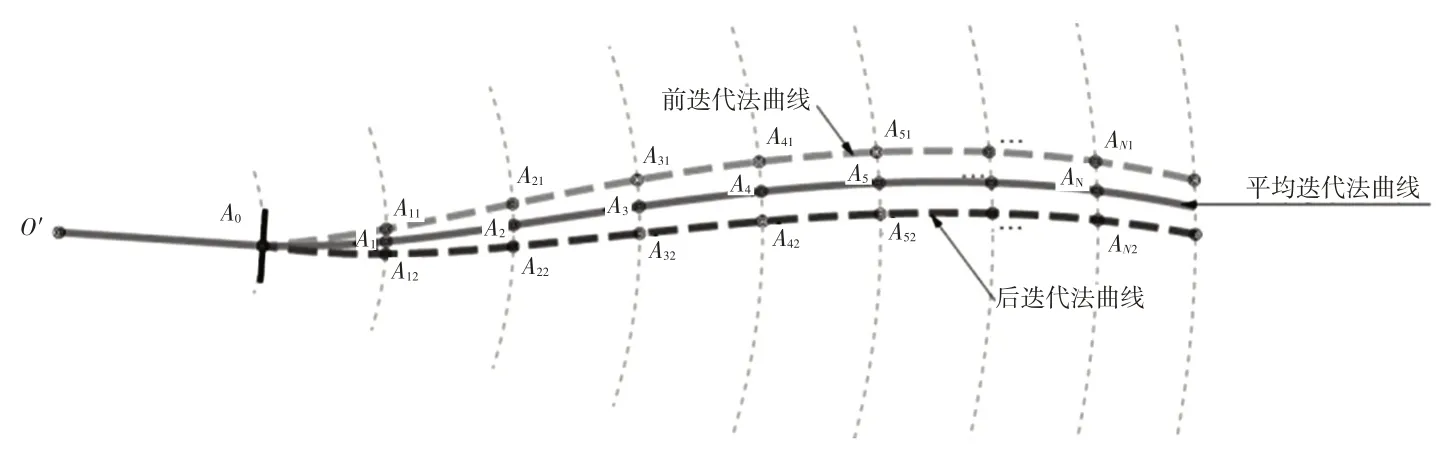
图6 平均迭代法曲线构造方法

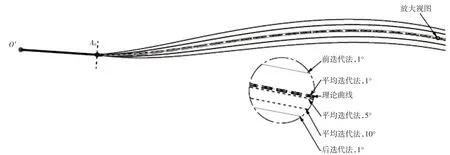
图7 前、后迭代法和平均迭代法求解结果与理论曲线对比

4.1 布置参数定义

在设计限位臂曲线时，为了获得最优方案，一般需要分析多种设计方案。如图9所示，O′和A0分别为限位器旋转中心和初始啮合点位置，n0和m0为限位臂中心线在A0点的切线单位向量和法向单位向量。O″和分别为优化方案中的限位器旋转中心和初始啮合点位置，和为优化方案限位臂中心线在点的切线单位向量和法向单位向量。分别以平行于和并指向整车坐标系X和Y轴正方向为H轴和V轴，建立参考坐标系VA0H。在新坐标系下，O″相对O′的坐标变化为（ΔHO′,ΔVO′），相对A0坐标的变化为(ΔHA0,ΔVA0)，相对m0的夹角为η（以逆时针角度为正）。显然，任意调整ΔHO′、ΔVO′、ΔHA0、ΔVA0和η、l、r1、ξ、α和σ都会对应发生变化。本文将分别研究改变ΔHO′、ΔVO′、ΔHA0、ΔVA0和η取值对限位臂曲线的影响规律。

图8 车门限位器包络及周边零件

图9 限位器布置参数定义

4.2 η对限位臂曲线的影响规律分析

设η为相对于m0转过的角度，由于m0和一般平行于限位器安装面，故η与冲压工艺性和布置空间关系较大。取η分别为0°、-3°和-6°，设置曲线参数，求得对应的曲线如图10 所示。由图10 可知，相对m0绕顺时针方向转过的角度越大，限位臂曲线偏向车身外侧方向越明显，而曲线长度变化不明显。

图10 不同η对应的中心曲线

4.3 ΔHO′和ΔHA0对限位臂曲线的影响规律分析

分别设置ΔHO′和ΔHA0为±5 mm，求得对应曲线如图11所示。从图11中可知：当O″和沿H轴方向靠近对方，即ΔHO′＞0 或ΔHA0＜0 时，限位臂曲线偏向车身内侧；当O″和沿H轴方向远离对方，即ΔHO′＜0 或ΔHA0＞0 时，限位臂曲线偏向车身外侧。ΔHO′的变化对曲线形状位置的影响较ΔHA0显著。

4.4 ΔVO′和ΔVA0对限位臂曲线的影响规律分析

分别设置ΔVO′和ΔVA0为±5 mm，求得对应曲线如图12所示。从图12中可知，ΔVO′和ΔVA0对限位臂曲线影响规律完全不同：ΔVA0对限位臂曲线位置影响较大，对曲线形状和长度影响不明显，改变ΔVA0，限位臂曲线的啮合段几乎都随平行移动；ΔVO′对限位臂曲线的长度影响较为明显，对限位臂曲线位置的影响不明显，ΔVO′越大，限位臂曲线越长。

任何限位器布置优化方案均能通过ΔHO′、ΔVO′、ΔHA0、ΔVA0和η进行表征，因此，在限位器布置方案优化过程中，可以结合上述规律，快速判断出限位臂曲线发生的变化，提高设计效率。

图11 O′和A0在H方向不同相对位置对应的中心曲线

图12 O′和A0在V方向不同相对位置对应的中心曲线

5 布置参数对限位器力学性能的影响规律分析

5.1 限位器力学分析

对限位臂进行受力分析，如图13 和图14 所示。限位臂受到限位盒沿中心曲线切向作用力Fx、法向作用力Fy以及平衡旋转轴摩擦力矩Tf的作用，其中Fx和Fy可以分别分解为限位臂正面和侧面受到沿中心曲线切向作用力Fx1、Fx2和法向作用力Fy1、Fy2。

限位器运动过程中，滑块始终沿着限位臂曲线切向滑动（α为常数），在法向近乎相对静止，所以|Fy1|≈0，故：

图13 限位器主臂受力情况

图14 限位器主臂对车门作用力分析示意

Fx1为限位器正面对滑块沿中心曲线方向的切向作用力，可以根据限位臂正面几何参数、滑块结构参数、摩擦因数以及滑块压荷等参数计算得到。

令μc为限位臂侧壁与滑块间的摩擦因数，则有：

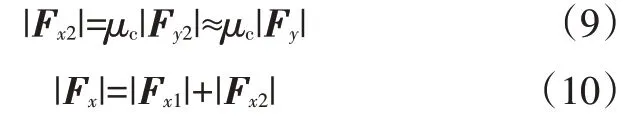
Fx和Fy的合力Fh沿着O′A′方向，一般地，Fh与Fx夹角较小，与Fy夹角较大，|Fy|明显小于|Fx|，所以|Fx2|＜＜|Fx|，故：

定义限位器布置参数如表2所示，通过Adams建立限位器仿真分析模型，如图15 所示。分析得到Fx1、Fx2及Fy1、Fy2随车门开启角度θ的变化曲线，如图16 所示。从分析结果可知，|Fy1|＜＜|Fy2|，|Fx2|＜＜|Fx1|，说明上述力学分析和假设成立。

表2 限位器仿真分析模型参数定义

Fh可分解为沿r1方向的分力Fr和垂直与r1方向的分力Ft，由于Fh平行于r2，所以：

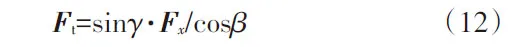
图15 限位器仿真分析模型

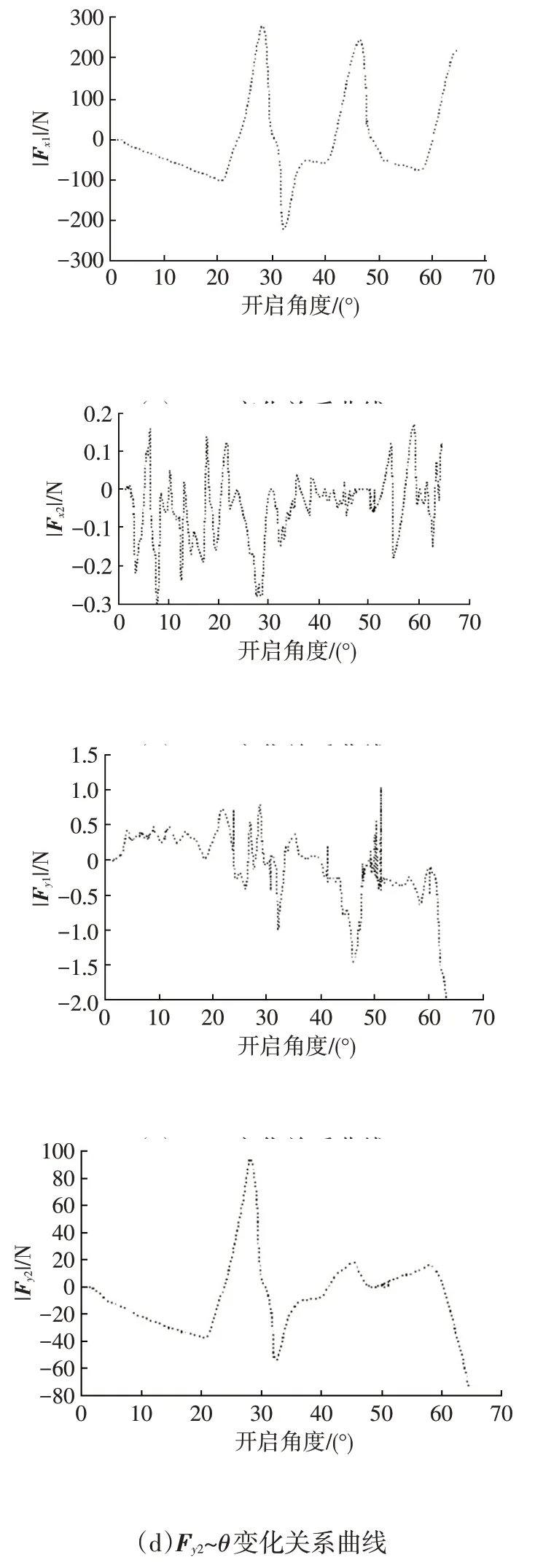
图16 限位器主臂受力仿真分析结果

根据三角形几何关系可求得：

令

限位器作用于车门的力矩T为：

联立式（12）～式（15）可得：

从式（16）可以看出，d(θ)代表限位力的真实力臂，它是受ξ和α影响的、与θ相关的函数。通过式（16）和前述Adams仿真分析模型可以分别得到d(θ)随θ的变化关系曲线，如图17所示。从图17中可知，由于是按动力学过程仿真，运动过程存在非平衡扰动，仿真结果围绕理论值存在一定波动，但总体变化规律一致。

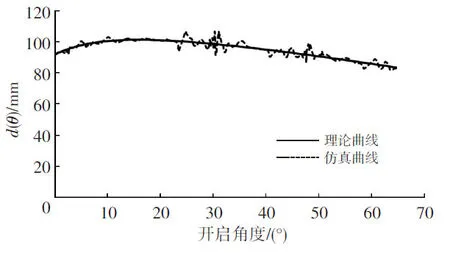
图17 d(θ)随θ变化的理论和仿真分析曲线

5.2 d(θ)的几何含义

过O做n的垂线与O′A′或其延长线相交于B′，OB′与n交于BC′，则∠C′B′A′+β=π/2，可得：

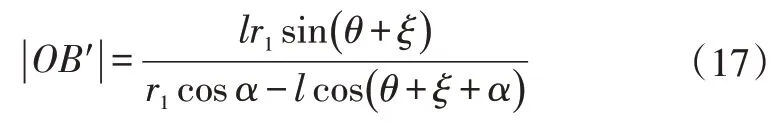
显然，|OB′|=d(θ)，所以OB′即为限位力的真实力臂。工程上，可以通过作图法测出不同开启角度下OB′的长度，从而快速求得不同车门开度下的限位力矩。

5.3 布置参数对d(θ)的影响规律研究

从式（16）可知，d(θ)的变化影响着限位力矩的变化。由式（14），分析l和r1对d(θ)的影响如下：

a.令r1=114 mm、ξ=13°、α=53.2°，取l分别为130 mm、114 mm、100 mm 和85 mm，得到d(θ)随θ的变化曲线，如图18所示。从图18中可知，d(θ)随l单调变化，l越大，d(θ)越大。

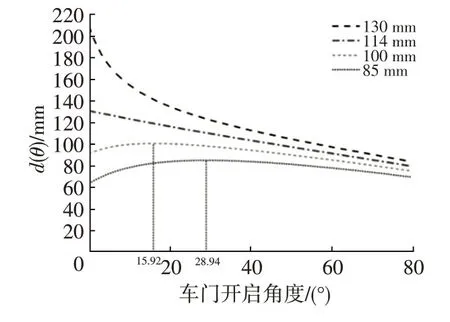
图18 不同l取值下d(θ)随θ的变化曲线

b.令l=100 mm、ξ=13°、α=53.2°，取r1分别为90 mm、100 mm、114 mm 和120 mm，得到d(θ)随θ的变化曲线，如图19 所示。从图19 中可知，r1对d(θ)的影响与(θ+ξ+α)有关：0＜θ+ξ+α＜π/2 时，r1越大，d(θ)越小；π/2＜θ+ξ+α＜3π/2 时，r1越大，d(θ)越大；θ+ξ+α=π/2时，d(θ)不受r1影响。

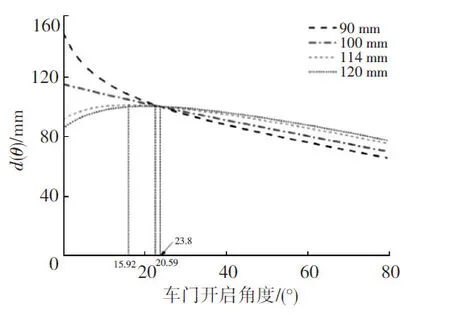
图19 不同r1取值下d(θ)随θ的变化曲线

从上述分析可以发现，l和r1不仅影响d(θ)大小，也影响着d(θ)随θ的变化规律。对d(θ)求导可得：

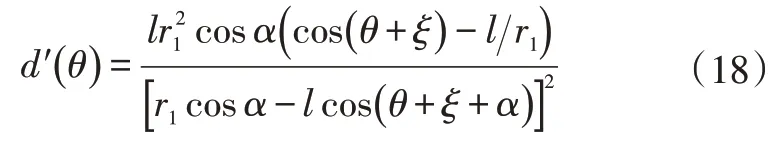
由于0＜α＜π/2，从式（18）可知，d(θ)随θ的变化规律为：当l/r1≥1 时，d′(θ)≤0 恒成立，d(θ)随着开启角度θ增大而减小；当l/r1＜1 时，d(θ)随着开启角度先增大后减小。在θ=arccos(l/r1)-ξ时，d′(θ)=0，此时d(θ)最大，d(θ)max=l/sin[arccos(l/r1)+α]。d(θ)max也与α有关，当α=arcsin(l/r1)时，d(θ)max最小，等于l/r1，如图20 所示。从图20中可知，α不影响d(θ)的总体变化趋势，但影响其变化幅度，α越大，d(θ)变化幅度越小。

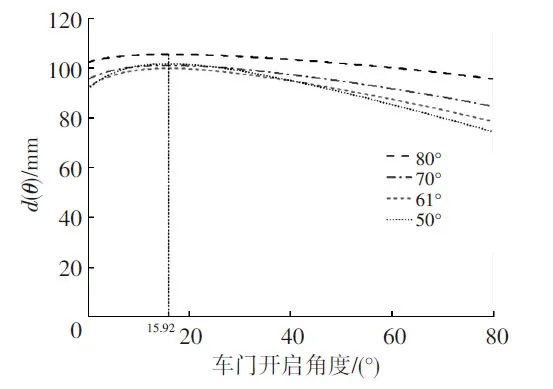
图20 不同α取值下d(θ)随θ的变化曲线

5.4 布置参数对β(θ)的影响规律研究

对限位臂进行受力分析可知：

一般地，为了保护限位臂及滑块，以及能够更加准确地设计限位力，优化限位器布置方案时通常尽量减小Fy和Fx2，因此，需要尽量减小β。

因为γ=α+β，由式（19）可得：

所以β也是关于θ的函数，记为β(θ)，从式（20）可知，l和r1对β(θ)的影响都是单调的，l越大，β(θ)越大（见图21）；r1越大，β(θ)越小（见图22）。

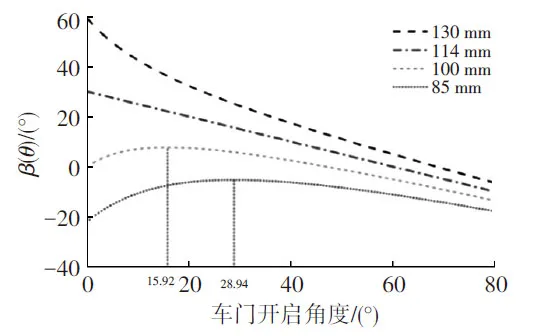
图21 不同l取值下β(θ)随θ的变化曲线

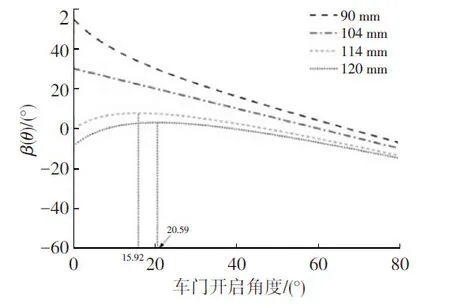
图22 不同r1取值下β(θ)随θ的变化曲线

可以证明，β(θ)与d(θ)具有相同单调性：当l/r1≥1时，β(θ)随θ增大而减小；当l/r1＜1 时，β(θ)随θ先增大后减小。当θ=arccos(l/r1)-ξ时，β(θ) 最 大，此 时β(θ)max受α的影响如图23 所示：当α＜arcsin(l/r1)时，β(θ)max＞0；当α=arcsin(l/r1)时，β(θ)max=0；当α＞arcsin(l/r1)时，β(θ)max＜0。从图23中可知，α越小，β(θ)越大，改变α，能整体改变β(θ)。

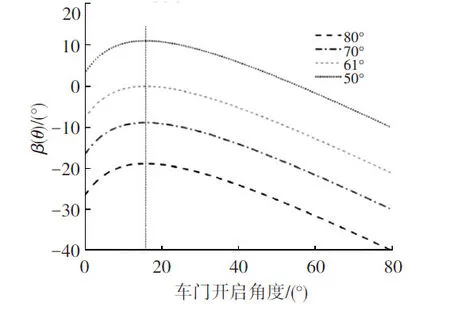
图23 不同α取值下β(θ)随θ的变化曲线

从上述分析可知：l和r1均对β(θ)存在影响，l越大，r1越小，β(θ)将越大；通过调节l/r1，可以改变β(θ)随θ的变化规律，以及β(θ)的变化幅度。一般建议l/r1＜1，且适当减小l/r1，增大β(θ)最大值对应的角度，以减小β(θ)的变化幅度。通过合理调节α，将α设计成适当小于arcsin(l/r1)的角度，可以使得β(θ)始终在0°附近的较小角度内变化。工程上，一般建议将|β(θ)|设置在15°以内。

6 结论

a.当车门及限位器布置参数l、r1、ξ、α和σ确定后，根据限位器主臂曲线方程即可求解出限位器主臂曲线；

b.相较于前、后迭代法，更建议采用平均迭代法进行手工绘制高精度限位器主臂中心曲线；

c.ΔHO′、ΔVO′、ΔHA0、ΔVA0和η对限位臂曲线有着不同的影响规律，在优化限位器曲线时，可结合相应规律，提高设计效率；

d.设计限位器时，目标是使得d(θ)尽量大，而|β(θ)|尽量小，l、r1、α对d(θ)和β(θ)的影响规律较为复杂，设计中应结合其影响规律进行反复优化。一般建议适当减小l/r1，使得l/r1＜1，同时，应使α＜arcsin(l/r1)。