基于驾驶特征学习的自动驾驶车辆换道轨迹规划＊

黄辉 隗寒冰

（重庆交通大学，重庆 400074）

主题词：轨迹规划 驾驶特征 成本优化 逆强化学习

1 前言

自动驾驶车辆需要在换道轨迹规划时反映拟人化需求，以提高行驶平顺性及乘坐舒适性，避免换道过程中引起驾乘人员不适。因此，学习驾驶员轨迹特征在自动驾驶车辆换道轨迹设计中具有十分重要的现实意义。

国内外学者对车辆轨迹规划问题已进行了广泛研究[1]。规划方法按照原理可大致分为图搜索、数值优化、插值法和采样法。目前，基于轨迹采样与成本函数优化相结合的方法作为主流的轨迹规划方法被广泛应用于自动驾驶车辆。如M.Werling等[2]以轨迹采样与成本函数优化相结合的方法规划轨迹，实现各换道场景的轨迹生成。该方法规划的换道轨迹基本满足换道行为功能需求，但忽略了驾驶员驾驶行为特征因素[3]。

在换道轨迹规划中考虑驾驶员换道特征，即拟人化换道轨迹规划，是近年来研究的热点。如黄晶[4]等运用K均值聚类法将驾驶风格分类，结合舒适性约束及换道行为数据进行不同驾驶风格换道轨迹规划，但忽略了轨迹曲线特征。Schnelle 等[5]提出了组合驾驶员模型和确定驾驶员期望路径的方法，对驾驶员模型和所需路径参数进行优化，仅考虑了驾驶员的横向控制，无法反映驾驶员的速度特征及行驶轨迹曲率特征。X.He 等[6]提出从自然驾驶数据中学习仿人轨迹规划方法，以softmax函数建立轨迹的概率模型，但该方法存在奇异值问题与学习特征上的局限。

机器学习方法被用来从人类演示的数据中学习成本函数或参数设置，研究成果同样应用于自动驾驶。Abbeel等[7]通过逆强化学习策略学习驾驶特征。Ziebart等[8]为了解决逆强化学习中存在的奇异值问题，将逆强化学习扩展到基于最大熵的方法。但这些研究都限于全局路径规划问题，而且更偏向于驾驶员路径选择的离散空间问题。Kuderer 等[9]运用最大熵逆强化学习策略学习轨迹特征后应用到局部轨迹规划中，在学习过程中通过最大似然求解二维空间中六自由度无穷轨迹的最大熵模型，该方法存在计算量庞大的弊端。

为生成反映驾驶员特征的换道轨迹，本文开展基于最大熵逆强化学习策略的换道轨迹特征学习方法研究，以轨迹采样方法为基础，对学习过程中的计算进行简化，通过轨迹采样与成本优化相结合的方式规划换道轨迹。

2 基于逆强化学习的换道轨迹规划

轨迹采样与成本优化相结合的方法主要思路是依据设计的成本函数筛选采样轨迹以生成最优轨迹。为了平衡轨迹规划的效率、舒适性、安全性，成本函数项权重需要基于专家经验设计，调试过程繁杂，具有一定的局限性。为解决目前存在的弊端，生成与驾驶员换道特征相匹配的轨迹，本文通过逆强化学习方法从驾驶员自然换道轨迹数据中迭代学习成本函数权重，并基于轨迹采样的方法优化学习过程中的迭代计算，使自动驾驶车辆能够规划出与人类驾驶员驾驶特征相近的换道轨迹。基于逆强化学习的换道轨迹规划流程如图1所示。

基于逆强化学习的换道轨迹规划由轨迹规划、驾驶特征建模及逆强化学习过程组成。在某一轨迹规划周期τ中，轨迹规划部分首先依据换道规划起点、终点的车辆坐标及其关于时间的一阶微分及二阶微分状态，通过轨迹采样的方式，生成备选换道轨迹序列TS=(Ts1,Ts2,Ts3,…,Tsn)，驾驶特征建模部分采集驾驶员换道轨迹离线坐标点，以多项式曲线拟合方式构建驾驶员换道轨迹TD=(TD1,TD2,TD3,…,TDn)，依据设计的轨迹特征函数向量f(TD)计算驾驶员换道轨迹各成本项的经验特征值。为解决轨迹分布中存在的奇异值问题[8]，将轨迹特征函数向量f(T)与备选轨迹序列TS依据最大熵原理构建轨迹的最大熵模型pMaxEnt，其中T为任意轨迹集输入，再依据最大熵模型求解各备选轨迹的期望特征值Ep[f]。通过梯度变化迭代调整轨迹特征函数中的各成本项权重向量系数λ，使得经验特征值与期望特征值Ep[f]尽可能接近：

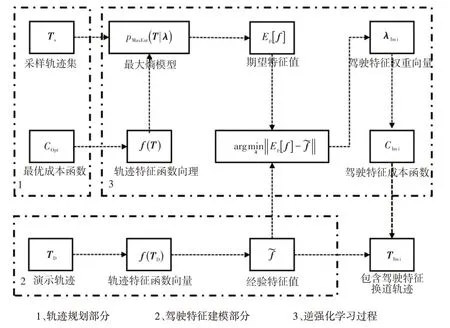
图1 基于逆强化学习的换道轨迹规划流程

当期望特征值Ep[f]与经验特征值的差值收敛于最小值时，便得到表征驾驶员轨迹特征的权重向量λImi。依据λImi分配各成本函数项权重比，重新调整驾驶员特征成本函数CImi，最后通过CImi筛选采样轨迹序列，以生成与驾驶员换道特征相匹配的换道轨迹。

3 轨迹规划方法

对自动驾驶车辆局部轨迹规划问题进行简化，同时便于轨迹特征函数定义，采用曲线坐标系为参考坐标系。在结构化道路下进行轨迹规划时，曲线坐标系通常以道路中心线作为参考线，将驾驶轨迹规划问题分解为沿道路中心线方向及其切线的法向量方向进行规划处理，图2所示为笛卡尔坐标系与曲线坐标系的转化关系。

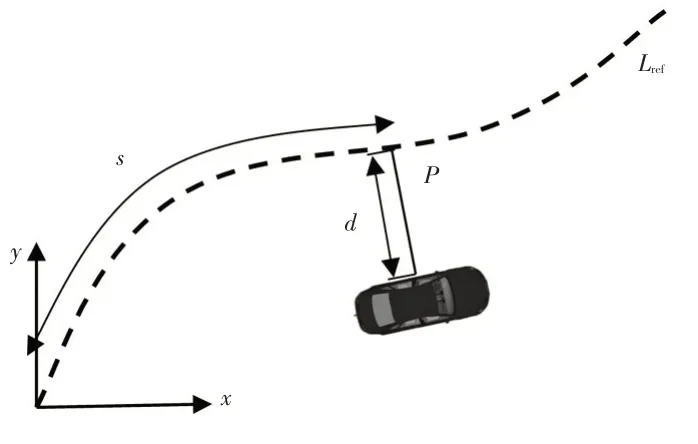
图2 笛卡尔坐标系与曲线坐标系的转化关系

不同于笛卡尔坐标基准(x,y)，曲线坐标系是以车辆位置与参考线投影点P之间的距离d为纵坐标，以参考线起始点到投影点P的曲线长度s为横坐标建立曲线坐标系基准(s,d)[10]。坐标系之间的映射关系与转化关系表示为：

式中，x为笛卡尔坐标系下的车辆位置坐标向量；s(t)、d(t)分别为t时刻车辆位置到参考线Lref上投影点的弧长距离与法向距离；nr(s(t))为投影点的单位法向量；r(s(t))为投影点上的位置向量。

为保证换道轨迹曲率、速度、加速度上的连续性及轨迹边界条件的完整性，采用五次多项式曲线拟合换道轨迹。根据峰值加速度准则，五次多项式函数比其他路径函数更具舒适性优势[11]。在任意t时刻，换道轨迹可以表示为：

式中，a0～a5与b0～b5分为d、s方向上五次多项式函数的系数。

当换道轨迹的起点、终点状态确定时，可依据五次多项式换道轨迹推导出其一阶微分及二阶微分状态。起点状态由换道时的纵向速度及偏离道路中线距离决定，终点状态依据换道任务的纵向偏移距离及目标车速定义。在一个规划周期τ中，五次多项式的系数可由起点、终点状态及其一阶、二阶微分状态求解得到，规划周期τ由规划起点时刻ts与规划终点时刻te决定。

在每个规划周期中，依据s、d方向起始状态及终点状态的采样，依据五次多项式函数便可规划出一系列备选换道轨迹序列集TS。

4 驾驶特征建模

通过采样方法生成备选换道轨迹集后，还需定义合理的成本函数用于备选换道轨迹筛选。本文的研究目标是从驾驶员换道轨迹中学习驾驶轨迹特征，因此，成本函数应为考虑更加全面且能表征驾驶员特征的成本函数项，同时为逆强化学习过程需求定义合理的特征函数。考虑如下成本函数项：

在整个换道轨迹中，以轨迹曲线函数在任意一点的三阶微分量表征换道过程中的冲击度特征J，整个换道轨迹s、d方向上的冲击度特征成本CJ定义为：

以轨迹曲线在某一点上的二阶微分量表征换道过程中的加速度特征a，整个换道轨迹s、d方向上的加速度特征成本Ca定义为：

以换道轨迹曲线上某一点处的曲率为曲率特征κ，整个换道轨迹上的曲率特征成本Cκ定义为：

以换道过程中s方向实际速度与期望速度偏差量vdev定义特征成本Cvdev：

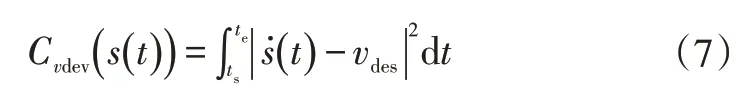
以换道轨迹偏离道路中线Lref(τ)的距离ddev定义特征成本Cddev：

通过将设计的各成本项整合，同时分配权重系数便构成完整的成本函数COpt：

式中，λ N为每个成本项的系数权重向量；N为成本函数的最大指数系数；C=(CJ(s(t)),CJ(d(t)),Ca(s(t)),Ca(d(t)),Cκ(s(t),d(t)),Cvdev(s(t)),Cddev(d(t)))为成本项向量。

本文通过逆强化学习的方法学习得到权重向量系数λ，实现各成本项还原驾驶员特性分配。依据设计的成本函数定义逆强化学习中的特征函数向量f：

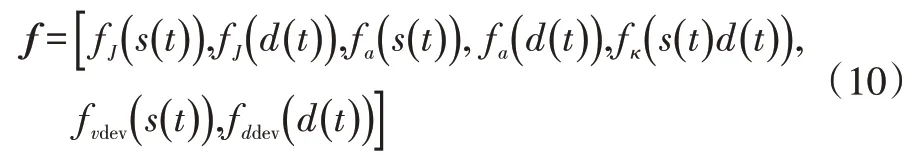
式中，fJ(s(t))、fJ(d(t))分别为s、d方向上的冲击度特征函数；fa(s(t))、fa(d(t))分别为s、d方向上的加速特征函数；fκ(s(t),d(t))为s、d方向上的曲率特征函数；fvdev(s(t))为s方向上的速度偏差特征函数；fddev(d(t))为d方向上的距离偏差特征函数。

依据驾驶员多次自由换道情况下的离线换道轨迹点，拟合出一系列换道轨迹曲线TD=(TD1,TD2,TD3,…,TDn)，依据特征函数向量f计算出逆强化学习过程中驾驶员轨迹经验特征值：

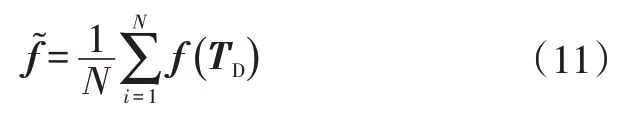
5 逆强化学习

逆强化学习的目的是生成与演示结果相似的轨迹，以特征值为相似性的评判度量。逆强化学习的关键是找到预期的参数λ使得期望特征与观察到的经验特征相匹配。以采样轨迹为基础，构建轨迹的最大熵概率模型pMaxEnt，优化问题的最大熵模型有如下形式：

式中，Z(λ)为满足归一化条件的正规化因子，归一化条件为：

将λTf(TS)解释为成本函数，与轨迹规划部分的成本函数COpt相对应，可以理解为驾驶员更有可能选择成本较低的轨迹进行换道轨迹规划。权重向量参数λ的解析解通常无法计算，但可以计算关于λ的拉格朗日函数的梯度，该梯度是期望值与经验特征值的差值：

通过对演示轨迹TD求对数似然函数得到：

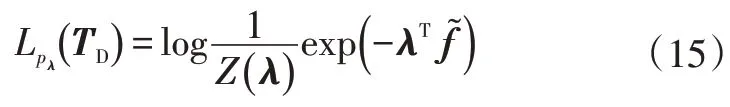
求其关于λ的一阶微分为：

式中，pλ(T)为λ权重下关于任意轨迹输入的概率。

通过基于采样的轨迹生成方法，可以简捷地计算出期望特征值：

选择合适的采样轨迹数量可以优化逆强化学习过程中的计算量。基于特征匹配的最大熵分布问题等价于假设指数族分布时训练数据的最大似然问题，从而将目标转化为找到符合预期的一组演示的特征分布。找到期望的分布意味着计算参数权重向量λ，使得期望特征值与经验特征值相匹配。参数向量λ无法求解，但可以根据这些参数计算梯度，从而应用基于梯度的优化。梯度调整优化过程通过计算特征函数的全微分，同时控制步长使函数到达极小值。对于部分特征项不可解析的计算梯度，可采用数值积分及解析导数相结合的方式计算。曲率特征梯度的近似求解公式为：

式中，Δt为在规划周期τ内的采样周期。

基于逆强化学习方法学习驾驶员换道轨迹特征的权重分配算法流程如图3所示。

通过逆强化学习过程学习到权重向量λ后，依据λ为成本函数COpt各成本项分配权重筛选备选轨迹，便实现了包含驾驶员特征的换道轨迹生成。

6 试验验证与结果分析

为验证本文提出的基于逆强化学习的换道轨迹规划的有效性，在“行远”自动驾驶车辆试验平台[12]上开展试验，分别执行驾驶员换道轨迹点采集与实时换道轨迹规划及跟踪控制任务。驾驶员换道轨迹点处理及逆强化学习过程均离线完成。试验平台硬件配置如图4 所示：感知系统由双目摄像头及激光雷达构成；定位系统配置差分GPS用于实现厘米级车辆定位与导航；所有算法部署在车载工控机上以实现车辆的感知、定位、决策、规划及控制。

图3 学习驾驶员换道特征分配权重算法流程

图4 “行远”自动驾驶车辆试验平台

以重庆交通大学校园试验区作为试验场景分别进行驾驶员1、驾驶员2 换道轨迹点的采集工作。试验场地如图5a 所示，其为标准单向双车道场地。驾驶员进行自由换道操作，仅收集驾驶员从右向左的换道轨迹，且驾驶员每次换道仅跨越1 个车道位置。考虑校园试验场场景，规定驾驶员理想换道车辆速度为35 km/h。为了提高轨迹的随机性，不预先告知驾驶员采集任务，仅告知其需控制车速在35 km/h附近自由换道操作。

共采集到2名驾驶员有效换道轨迹20条，平滑滤波处理后驾驶员换道轨迹如图5b、图5d所示。2名驾驶员均具有3～5 年驾龄，能够稳定执行换道操作，依据换道轨迹集边界定义驾驶员换道区域如图5c、图5e 所示。在曲线坐标系下，依据换道轨迹点横、纵坐标以及每个轨迹点的时间序列，拟合s、d方向上的五次多项式函数，并依据式（11）计算出驾驶员各换道特征经验特征值，统计结果如表1所示。相比于驾驶员换道轨迹纵向相关特征，横向相关特征更为显著。

图5 校园试验场及驾驶员换道轨迹

将驾驶员换道轨迹经验特征值代入逆强化学习过程中进行迭代学习，如图6 所示，基于梯度下降的权重系数调整策略导致特征值差值曲线出现微小振幅，而非单调下降。在经过接近25次迭代后，2位驾驶员的经验特征值向量与期望特征值向量的差值基本收敛。由于轨迹规划基于采样的方式完成，仅能在轨迹集中筛选出最接近驾驶特征的某条轨迹，导致特征差值不为零。依据学习得到的权重向量λ，对规划系统的成本函数权重进行重新分配调整，依据调整更新后的成本函数筛选实时规划的备选轨迹。

表1 驾驶员换道特征值

图6 特征值差值迭代过程

图7所示为成本权重更新前、后实时轨迹规划对比情况。从图7中可以看出：未调整权重情况下实时车辆备选规划轨迹序列大部分偏离2 位驾驶员的换道轨迹区域；学习驾驶员1 换道特征后，车辆实时规划的换道轨迹基本包含在驾驶员1换道区域内，部分偏离驾驶员2换道区域；学习驾驶员2换道特征后，车辆规划的换道轨迹基本包含在驾驶员2换道轨迹区域内。

如图8、图9 所示，将成本权重更新前、后换道轨迹特征对比情况以百分率形式表现，即以驾驶员特征为基准。自动驾驶车辆局部轨迹规划系统在均等权重比下，s方向上的特征偏离基准较小，能较好地匹配，而在d方向上，调整前特征偏离基准较大。学习驾驶员特征后，特征偏离情况降低，向驾驶员特征靠近。对比调整前、后，表征乘员舒适度的纵向特征J与加速度特征a指标明显降低，且趋近于人类驾驶员换道操作水平，改善了换道过程中的乘员舒适性体验。

将驾驶员换道轨迹曲线及换道特征进行对比，结合成本权重更新前、后的试验结果可以发现：在均等成本函数权重下生成的轨迹部分偏离驾驶员换道轨迹区域，相对于驾驶员换道轨迹曲线，曲率变换更为剧烈，换道轨迹曲线特征除纵向特征外，较驾驶员各特征相差较远；通过逆强化学习方法更新成本权重后的规划轨迹基本包含在驾驶员换道轨迹内，换道轨迹曲线各特征与驾驶员特征相近，更能反映驾驶员主观感受。

图7 成本权重更新前、后轨迹规划对比

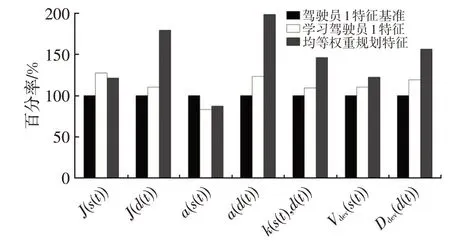
图8 学习驾驶员1特征对比

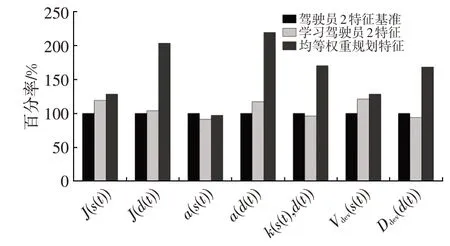
图9 学习驾驶员2特征对比

7 结束语

本文采用轨迹采样及成本优化相结合的轨迹规划方法设计了自动驾驶车辆轨迹规划算法。考虑换道规划过程中的驾驶员主观感受，运用最大熵逆强化学习策略从驾驶员换道轨迹中学习轨迹特征分配，并将学习得到的权重向量用于成本函数权重分配，依据更新后的成本函数在采样轨迹中筛选匹配，最终生成与驾驶员换道轨迹特征相近的换道轨迹。试验结果表明，本文开发的基于逆强化学习的换道轨迹能较好地包含在驾驶员换道区域内，且轨迹特征与驾驶员轨迹特征相近，即满足拟人化驾驶需求。