齿面均匀腐蚀后顶隙系数对面齿轮弯曲应力的影响

臧少峰， 刘忠亮， 胡锡文， 王 娟， 李晓贞*

(1.中国核电工程有限公司，北京 100840；2.安徽科技学院 机械工程学院，安徽 凤阳 233100)

面齿轮作为一种新型齿轮形式，因其具有结构简单、承载能力大、振动噪声小和对安装误差不敏感等优点，适合应用于核废料处理设备中，但由于其工作在腐蚀性环境中，有必要分析齿面腐蚀对面齿轮传动啮合特性的影响。

Litvin等对面齿轮进行了大量的研究，对面齿轮的推广起到了极其重要的作用。且面齿轮已成功应用于旋翼直升机以及汽车差速器上。相关学者对面齿轮传动进行的研究为国内面齿轮的研究与发展奠定了基础。大量学者在面齿轮弯曲应力计算方法、齿根弯曲强度、动态啮合性能以及接触特性等方面进行了大量的研究。彭先龙等分析了安装误差对面齿轮承载传动性能的影响，研究了基于面齿轮车桥总成构型，并通过了虚拟样机技术以及面齿轮车桥试验台的验证。

本研究根据正交面齿轮与圆柱齿轮的装配关系，通过调整装配间隙来模拟面齿轮齿面被均匀腐蚀程度，通过对不同腐蚀程度的正交面齿轮副模型进行瞬态动力学分析，探究接触区域位置的变化以及面齿轮齿根弯曲应力以及齿面接触应力随腐蚀程度变化的情况。为面齿轮腐蚀后传动特性研究提供参考基础。

1 正交面齿轮齿面方程设定

根据齿轮啮合原理，以及包络法求共轭齿面的方法，正交面齿轮包络加工过程中的刀具齿轮T和被加工面齿轮F存在4个加工坐标系，如图1所示。刀具齿轮T初始位时的坐标系为O-XYZ，被加工面齿轮F初始时的坐标系为O-XYZ是，随刀具齿轮T运动的坐标系为O-XYZ，随被加工面齿轮F运动的坐标系为O-XYZ。刀具齿轮初始时的坐标系O-XYZ与其运动坐标系O-XYZ的坐标原点O和坐标轴Z轴重合，且运动坐标系O-XYZ是由初始坐标系O-XYZ绕坐标系轴线O-Z转过角度φ后得到。同理，被加工面齿轮初始坐标系与运动坐标系的原点与Z轴重合，而固定坐标系O-XYZ绕轴线OZ转过角度φ后得到随动坐标系O-XYZ。图1中的参数ω_T和ω分别为刀具齿轮T和被加工面齿轮F转动的角速度；参数d为包络加工时刀具齿轮T的齿宽中心面OXY与被加工面齿轮F的轴截面OXY之间的距离，在包络加工过程中，参数d随刀具齿轮T的切削运动时位置的变化而不断变化；参数r为刀具齿轮T的分度圆半径。

图1 正交面齿轮包络加工坐标系

在面齿轮包络加工过程中，刀具齿轮与被加工面齿轮绕各自轴线的转动是模拟面齿轮传动中圆柱齿轮与面齿轮的啮合过程。因此刀具齿轮与被加工面齿轮的转角、转动角速度、齿数及传动比关系满足

q

=

N

/N

=

φ

/φ

=

ω

/ω

=1

/q

(1)

式中,

N

为被加工面齿轮的齿数；

N

为刀具齿轮的齿数；

q

和

q

为刀具齿轮与被加工面齿轮的传动比。根据图1所示的面齿轮包络加工过程中的坐标系关系，从刀具齿轮的随动坐标系

O

-

X

Y

Z

到其固定坐标系

O

0-

X

Y

0

Z

的齐次坐标转换矩阵为

(2)

由刀具齿轮的固定坐标系

O

0-

X

Y

0

Z

到被加工面齿轮的固定坐标系

O

0-

X

O

Y

0

Z

O

的齐次坐标转换矩阵为

(3)

由被加工面齿轮的固定坐标系

O

0-

X

Y

0

Z

到其随动坐标系

O

-

X

Y

Z

的齐次坐标转换矩阵为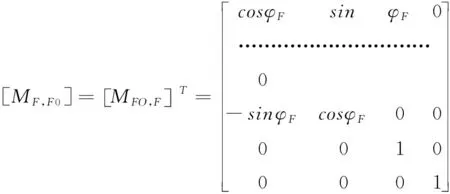

(4)

因此，根据坐标转换关系，由刀具齿轮的随动坐标系

O

-

X

Y

Z

到被加工面齿轮的随动坐标系

O

-

X

Y

Z

的齐次坐标转换矩阵为[

M

,]=[

M

,]=[

M

,0][

M

0,0][

M

0,]

(5)

式2～5中，各坐标转换矩阵中右上角标“T”表示矩阵的转置矩阵。

刀具齿轮的齿面是包络加工过程中的母面，是标准的渐开线齿面，其轴截面形状如图2所示。“a-a”和“b-b”分别表示齿槽的两侧齿面；

r

表示刀具齿轮的基圆半径；

α

表示刀具齿轮齿面上

k

点处压力角；

r

为刀具渐开线齿廓上任意一点

k

处的半径；

θ

为

k

点处的矢径与坐标轴

O

Y

的夹角；刀具齿轮的分度圆压力角用

α

表示，刀具齿轮的模数为

m

，齿数为

N

。

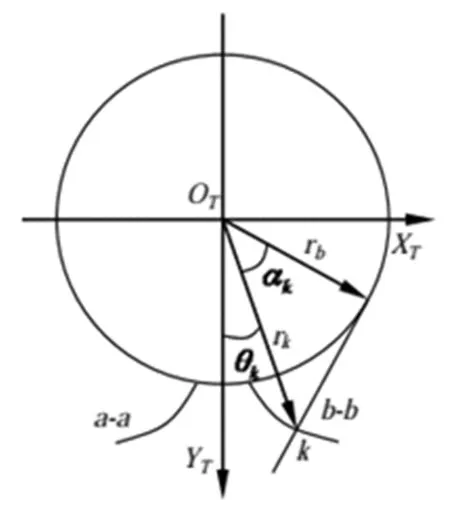
图2 刀具渐开线齿廓

根据齿轮的齿面几何关系，刀具齿轮的基圆半径由式6表示

r

=

m

N

cosα

/

2

(6)

刀具齿面上任一点

k

的半径

r

的表达式为

r

=

r

/cosα

(7)

k

点处的矢径与坐标轴

O

Y

的夹角

θ

的计算公式为

θ

=

π/

2

N

-

invα

+

invα

(8)

式中：

invα

=

tanα

-

α

，为刀具齿轮分度圆压力角的渐开线函数；

invα

=

tanα

-

α

为刀具齿面上

k

点处压力角的渐开线函数。

根据前文分析，得到刀具齿轮的齿面方程为

(9)

式中,

u

为沿刀具齿轮齿宽方向的参数变量；

X

中的“+”表示右齿廓“b-b”，“-” 表示左齿廓“a-a”。刀具齿面方程含两个参变量分别是刀具齿宽方向的参变量

u

和刀具齿面上

k

点的压力角

α

。刀具齿廓曲面方程从其随动坐标系

O

-

X

Y

Z

转换到面齿轮随动坐标系

O

-

X

Y

Z

后，得到在坐标系

O

-

X

Y

Z

中的刀具齿廓曲面方程为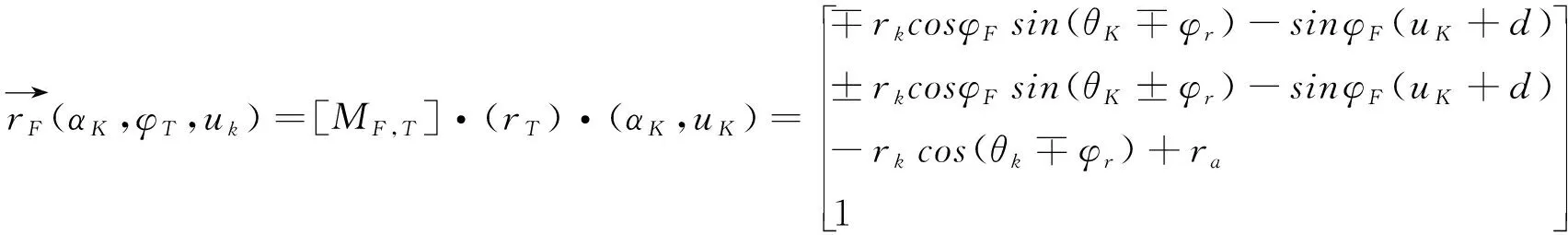

(10)

根据式7可知，

r

为含参数

α

的变量；根据刀具齿轮与面齿轮的传动比关系，

φ

=

φ

q

，故

φ

与参数

φ

有关的变量；由式8可知，

θ

为与参数

α

有关的变量。因此，刀具齿廓曲面在坐标系

O

-

X

Y

Z

中的方程含有3个变量参数，分别为

α

、

φ

和

u

。

根据包络原理，在面齿轮插齿加工过程中，刀具齿面与被加工面齿轮齿面之间满足的包络条件为

(11)

因此，将式10和11联立，得到刀具齿轮齿面通过包络加工得到的面齿轮齿廓曲面方程为

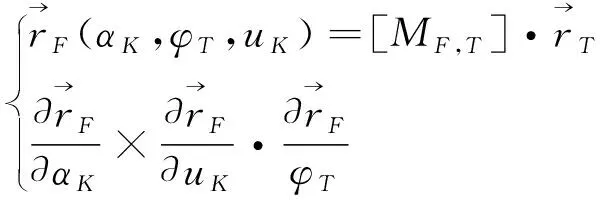
(12)

面齿轮齿面方程式12中的第一式含有3个参数变量

α

、

φ

和

u

，包络条件第二式也是含有3个参数变量

α

、和

u

，将包络条件中的参数变量

u

用另外两个参数变量

α

和

φ

表示，并带入第一式中，从而得到仅含参数变量

α

和

φ

的面齿轮齿廓曲面方程。

2 正交面齿轮模型的建立

通过对正交面齿轮齿面方程的推导可以看出，正交面齿轮齿面不再是一般的渐开线齿面，而是较为复杂的空间曲面，因此难以直接建立正交面齿轮三维模型。为此本文通过Visual Studio建立正交面齿轮建模程序，界面如图3所示。通过该程序计算出正交面齿轮单个齿面上的有限个数据点，将计算出的数据点导入到三维建模软件CATIA中，借助CATIA强大的曲面设计能力完成对正交面齿轮单个齿面的曲面建立，最后通过旋转、拉伸以及多截面实体等操作完成正交面齿轮三维模型的建立。

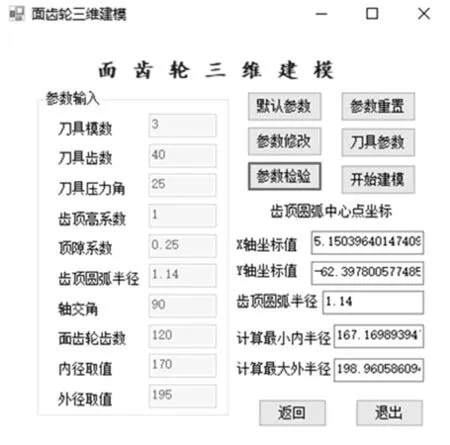
图3 面齿轮三维建模程序界面

本研究建立的正交面齿轮模型参数如表1所示，建立的三维模型如图4a所示。

表1 正交面齿轮模型参数

图4 正交面齿轮三维模型

根据面齿轮包络加工原理，刀具齿面与被加工面齿轮齿面是线接触。但由于不可避免的存在制造和安装误差，以及轮齿在受载时产生变形，导致理想的线接触变为边缘接触，使面齿轮传动中的轮齿受到偏载作用，影响其强度和动力学特性。为解决这一问题，通常采用传动中的圆柱齿轮比刀具齿轮的齿数少1～3个齿的方法，使面齿轮传动变为点接触的传动形式。为了仿真分析与实际情况更加贴近，建立圆柱齿轮相关参数如表2所示。

表2 圆柱齿轮参数

根据正交面齿轮与圆柱齿轮的参数，建立两者的正确装配体模型如图4b所示。

3 均匀腐蚀对面齿轮齿根弯曲应力的影响

3.1 均匀腐蚀程度的设置

参照普通标准圆柱齿轮装配关系，标准基本齿轮齿条与相啮合标准基本齿轮齿条之间的顶隙为Cp。本文根据圆柱齿轮配合标准将正交面齿轮与圆柱齿轮的配合顶隙设为Cp如图5所示，并将正交面齿轮齿面的均匀腐蚀程度转化为Cp值的变化，从而探究均匀腐蚀对正交面齿轮齿根弯曲应力的影响。

将正交面齿轮均匀腐蚀转化成顶隙变化后设置7组不同的Cp如表3所示。

图5 正交面齿轮与圆柱齿轮装配关系示意图

表3 不同腐蚀程度所对应的Cp值

3.2 均匀腐蚀后正交面齿轮应力有限元分析

通过对正交面齿轮均匀腐蚀的转化，设置7组不同程度的腐蚀程度。首先在建模软件中根据腐蚀程度对7组齿轮副模型进行装配，将装配好的模型导出为parasolid格式，并且保存在全英文的文件下，以便导入到ANSYS进行有限元分析。

使用ANSYS中的瞬态动力学模块对正交面齿轮与圆柱齿轮进行有限元分析。鉴于正交面齿轮尺寸较大，齿数较多，考虑到计算机性能，为了节约分析时间将正交面齿轮简化为三齿模型，圆柱齿轮简化为四齿模型。将简化后的齿轮副模型进行网格划分，采用四面体网格，并将单元格尺寸控制在3 mm进行划分，划分出的单元个数为20 111，节点数为94 588，划分出网格后的正交面齿轮模型、圆柱齿轮模型如图6所示，其接触参数设置见表4。

图6 模型网格划分

网格划分完成，在圆柱齿轮上添加0.1°/s的斜坡速度，在正交面齿轮上添加15 533.4 N·m的扭矩作为负载，仿真分析时间设置为1 s，其他接触参数设置如表4所示。

表4 接触参数设置

仿真分析结束后，得到正交面齿轮齿根弯曲应力以及齿面接触应力(图7～13)。

图7 无腐蚀情况下的正交面齿轮齿根弯曲应力与齿面接触应力

图8 腐蚀程度为0.372 mm时正交面齿轮齿根弯曲应力与齿面接触应力

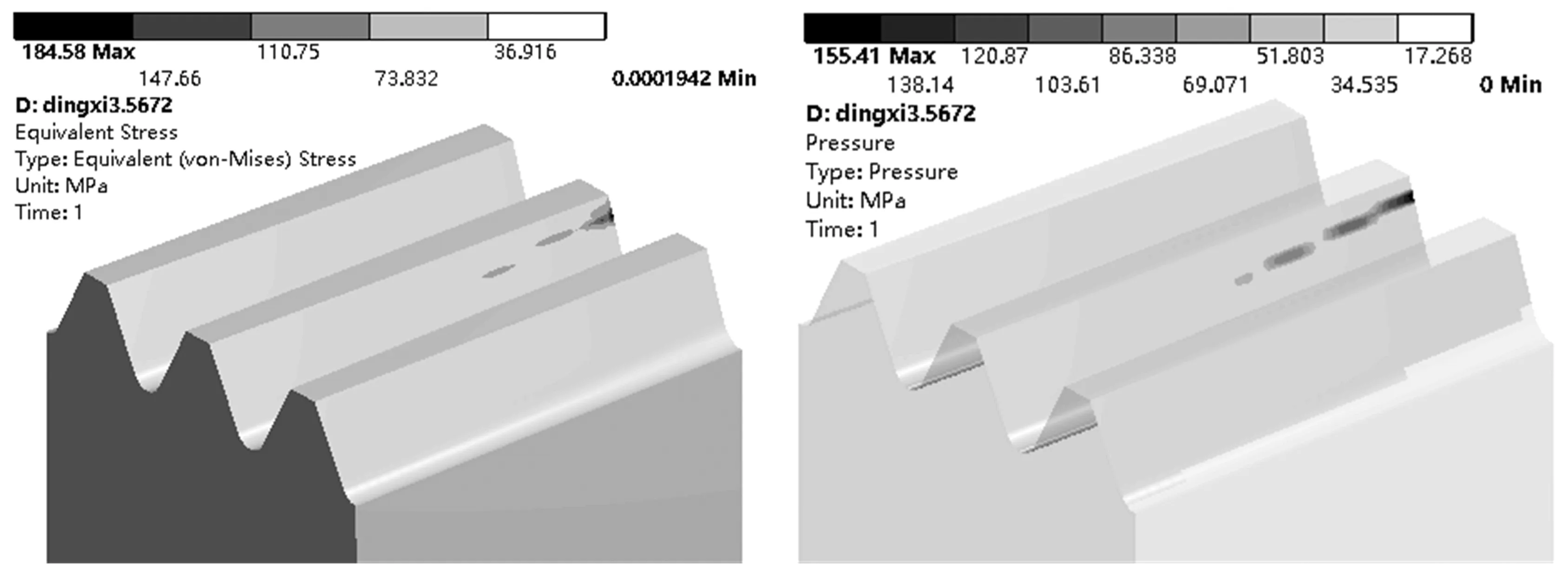
图9 腐蚀程度为0.745 mm时正交面齿轮根弯曲应力与齿面接触应力

图10 腐蚀程度为1.117 mm时正交面齿轮根弯曲应力与齿面接触应力

图11 腐蚀程度为1.490 mm时正交面齿轮根弯曲应力与齿面接触应力

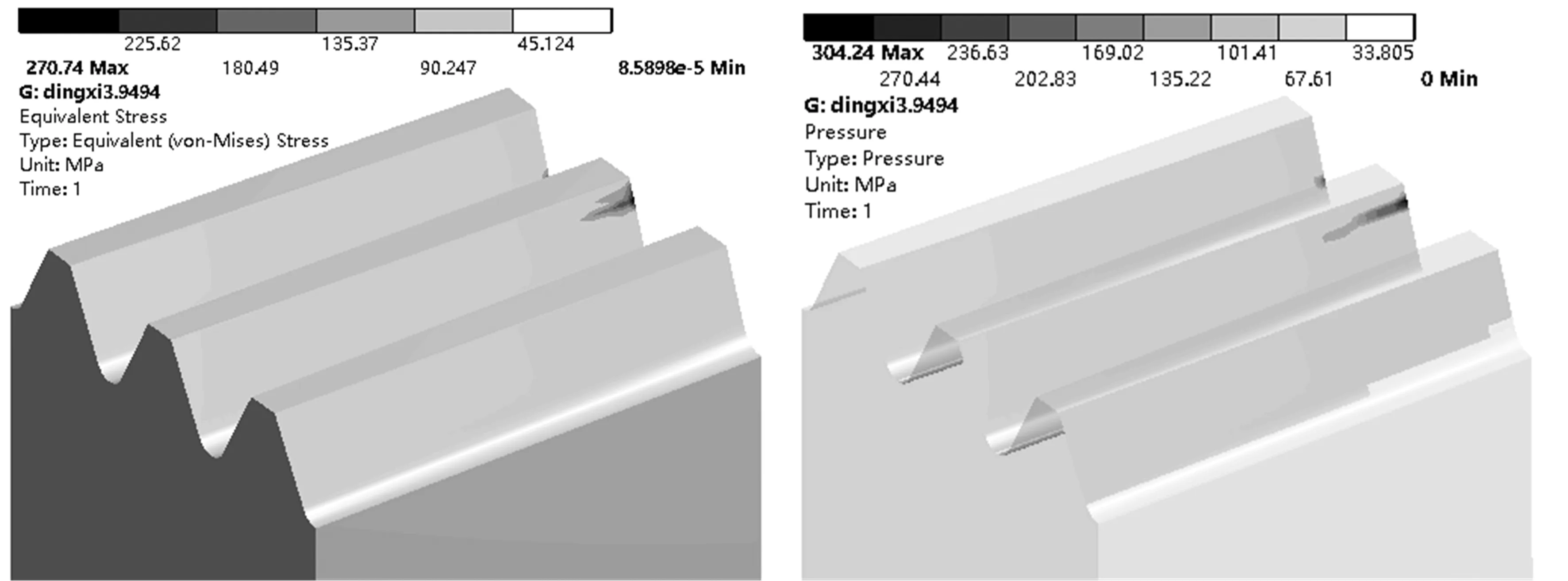
图12 腐蚀程度为1.862 mm时正交面齿轮根弯曲应力与齿面接触应力

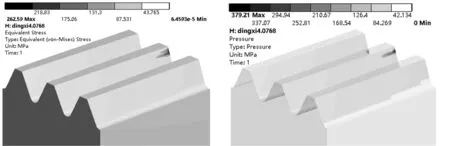
图13 腐蚀程度为2.235 mm时正交面齿轮根弯曲应力与齿面接触应力

图7～13中不同腐蚀程度对正交面齿轮齿根弯曲应力与齿面接触应力的影响如图14所示。

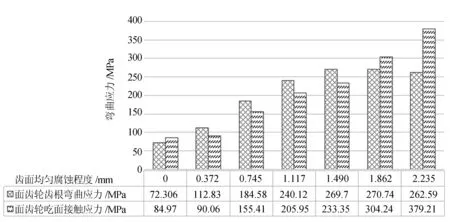
图14 不同腐蚀程度对面齿轮齿根弯曲应力与齿面接触应力的影响

从图7～13的正交面齿轮齿根弯应力云图与齿面接触应力云图可以看出，随着腐蚀程度的加深，圆柱齿轮与正交面齿轮的接触区域位置逐渐向齿顶方向以及面齿轮内半径方向偏移，当腐蚀程度达到一定程度，圆柱齿轮会在面齿轮内半径且偏于齿顶方向上的位置上产生接触，导致应力集中，此种腐蚀程度下在传动过程中圆柱齿轮齿面以及面齿轮轮齿产生会被破坏。导致传动过程无法正常进行。根据图14不同程度的腐蚀对面齿轮齿根弯曲应力与齿面接触应力的影响可以看出，当腐蚀程度小于0.372 mm时，基本对面齿轮的齿根弯曲应力与齿面接触应力的影响较小，后随着腐蚀程度的加深，面齿轮的齿根弯曲应力逐渐增大后趋于平缓，而齿面接触应力呈现出先增大后缓慢减小的趋势，这是因为正常接触区域被完全破坏导致的应力集中而造成的。

3 结论

本研究通过将正交面齿轮齿面均匀腐蚀程度转化为面齿轮与圆柱齿轮装配参数Cp的变化，通过有限元分析得到以下结论：

正交面齿轮齿根弯曲应力以及齿面接触应力随着面齿轮齿面腐蚀程度的加深而增大，最后达到应力极限。

正交面齿轮与圆柱齿轮的接触区域位置会随着腐蚀程度的加深，向面齿轮齿顶方向以及内半径方向偏移，当腐蚀达到一定程度产生边缘接触。

当均匀腐蚀程度较小时，面齿轮齿根弯曲应力与齿面接触应力变化不明显，从间接证明了正交面齿轮传动对安装误差敏感。