仿生叶片在离心风机上应用的数值分析

邬长乐， 陈二云， 杨爱玲， 李国平

(1.上海理工大学 上海市动力工程多相流动与传热重点实验室，上海 200093；2.上海船舶设备研究所，上海 200031)

离心风机作为旋转类机械家族中的一员，因其压头大、流量小的特点而被广泛应用于换气、通风等设备中。据统计，离心风机的用电量占全国发电量的5%左右[1]，在能源稀缺的大环境下，研制开发节能、高效的离心风机势在必行。此外，离心风机在运行时产生的噪声问题不容忽视，其振动和噪声有严格的限制标准。如何让离心风机保持高效率和低噪声的工作状态是近年来备受关注的研究热点之一。

离心风机的噪声源可分为气动噪声、电磁噪声和结构振动噪声，其中气动噪声约占总噪声的45%[2]，而叶轮作为离心风机唯一的动部件，其性能决定了离心风机整体的气动和噪声特性。自然界的许多动物经过长期演化，形成了出色的寂静飞行、无声游动等本领，如猫头鹰和座头鲸，受它们启发，仿生学原理为叶轮机械的增效降噪设计提供了新思路。Gruber等[3]在NACA65翼型基础上加装锯齿尾缘结构，通过实验发现该结构能降噪约5 dB。仝帆等[4-5]将SD2030翼型尾缘切成锯齿状，并将其安装在涡轮叶栅上，实验研究和数值模拟表明：锯齿尾缘翼型可降低层流边界层分离引起的涡脱落噪声，中低频下的宽频噪声也有所降低，但高频下噪声略有增大。焦跃等[6]对比了传统直锯齿尾缘和倾斜锯齿尾缘在降噪效果上的差异，发现倾斜锯齿结构可以明显削弱传统锯齿钝尾缘在低频段产生的窄带尖峰噪声。王绍兴[7]在轴流风机叶顶前缘、尾缘和前尾缘组合处进行锯齿处理，数值模拟结果表明：锯齿结构降低了吸力面和压力面的压差，减少了倒流，破坏了叶顶附近涡流，提高了风机全压和效率，且仿生轴流风机噪声至少降低了2.8 dB。Corsini等[8]发现正弦波浪形前缘可有效提高风扇的抗失速能力，当风扇处于峰值压比状态时，波浪形前缘可小幅提高风扇效率。Hansen等[9]通过实验发现NACA0021翼型前缘为波浪形时，层流边界层噪声明显下降，且振幅越大、波长越小，降噪效果就越好。Chen等[10]通过实验研究了波浪形前缘对NACA0012翼型不稳定噪声的影响，得到类似Hansen等的结论，并揭示了其降噪机制，即波浪形前缘翼型在波谷处会产生流向涡，增强了边界层内动量交换，影响了边界层的稳定性，削弱甚至破坏声学反馈回路。陈子龙[11]将凹坑结构引入NACA6510表面，通过风洞实验并结合数值计算，发现该非光滑表面结构将叶片尾迹区大尺度涡破碎成小尺度涡系，减少了速度亏损，降低了叶片的辐射噪声。

虽然现有针对翼型的仿生结构多种多样，但鲜有研究将其应用在离心风机叶片上。笔者将正弦波形前缘(下文简称波形前缘)、倾斜锯齿尾缘(下文简称锯齿尾缘)及凹坑非光滑表面(下文简称表面凹坑)等仿生结构引入小型离心风机叶轮，通过数值计算，探究了仿生离心风机流场和声场的分布规律，并对比分析了这些仿生结构对离心风机增效和降噪的影响，为离心风机的优化设计提供参考。

1 数值计算方法

1.1 几何模型及边界条件

笔者所研究的离心风机原型为后弯式离心风机，设计工况下其体积流量为qV=4 000 m3/h，全压Δp=1 200 Pa，转速n=2 900 r/min，叶片数为19，采用NACA-Yang翼型造型。进口安装角β1从叶根处的25°近似线性变化至叶顶处的31°，出口安装角β2=39°[12]。3种仿生叶片模型如图1所示。

图1 仿生叶片模型

Fig.1 Bionic blade model

图1(a)中的波形前缘结构由2个正弦波叠加而成，其设计公式为：

(1)

式中：hi为正弦波形振幅,h1/C=h2/C=2.5%，C为弦长；bi为角频率，bi=2πC/λi，λi为波长，λ1/C=25%，λ2/C=8.3%。

图1(b)为锯齿尾缘叶片，齿宽λ=0.12C，齿高h=0.5(h1+h2)=0.112C，斜切角φ=30°(φ为斜切方向与翼型中弧线切线之间的夹角)。

图1(c)为表面凹坑结构，凹坑布置在叶片吸力面上距前缘65%C处，坑间距s=2.5 mm，坑深度δ=0.5 mm，坑直径d=2.5 mm。

采用多域方法处理计算域，整机划分成3个计算子域，分别为进口域、叶轮域以及蜗壳和出口合并而成的一个域，如图2(a)所示，为确保进、出口气流均匀稳定，进出口段均延长了5倍管道当量直径。定常计算共设计5组工况，分别为0.6qV、0.8qV、qV、1.1qV和1.2qV，非定常计算只在设计体积流量qV下进行。由于来流最大马赫数为0.086，故可认为离心风机内的流体是不可压缩的。给定速度进口、压力出口边界条件，固体壁面为无滑移壁面边界条件。

定常计算选用两方程湍流模型中的可实现k-ε模型，采用多参考系(MRF)方法，各子域独立求解控制方程，流场信息的传递通过interface面实现；非定常计算采用大涡模拟(LES)方法，用MRF模型提供的定常收敛解作为初场，通过滑移网格技术获取瞬态信息。时间步长取叶轮每旋转1°所用时间，由式(2)求得Δt=5.747 126×10-5s。共计算3 600步(叶轮转10圈)，完成前5圈非定常计算后，开启FW-H方程求解声场，声源积分面除叶片表面外还包括蜗壳和管道等壁面。压力脉动测点布置在叶轮出口半叶高处的蜗壳壁面附近，沿流向共布置6个测点，如图2(b)所示。

(2)

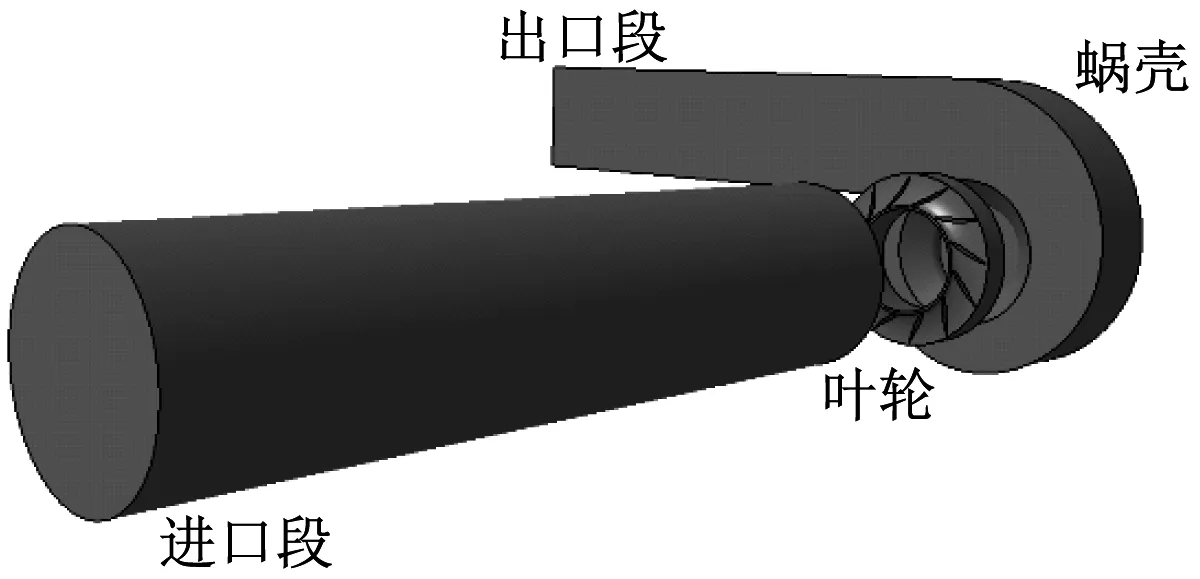
(a) 整机计算域划分

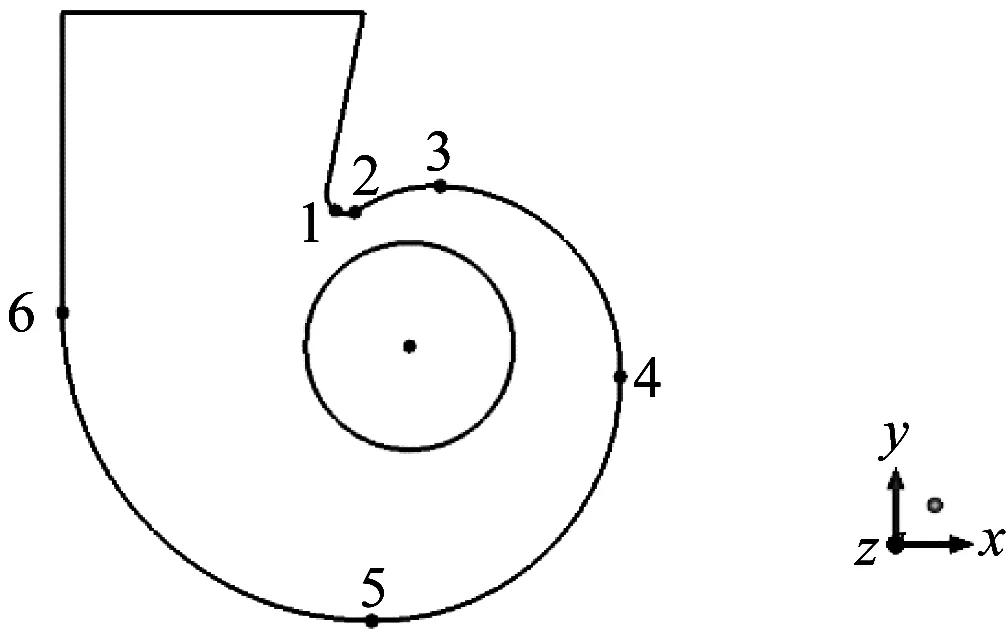
(b) 压力脉动测点

1.2 网格划分及其无关性验证

以波形前缘型风机为例，叶轮域内部分网格如图3所示，由于叶片前缘、尾缘处曲率变化大，易发生流动分离，为充分捕捉流场信息，对网格进行加密处理。此外，在各仿生叶片仿生结构位置处同样设置了网格局部加密区。

(a) 叶片表面网格

(b) 叶片边界层网格

(c) 叶片壁面y+值

壁面首层网格高度为0.015 mm，增长率取1.09，共25层，图3(c)为LES方法计算后的结果，叶片壁面附近y+值控制在1左右[13]，满足大涡模拟对网格的要求。由于改型部件为叶轮，故设计了4套不同密度的原型叶轮域网格，其他域网格数保持一致。图4(a)给出了设计体积流量下的无关性验证结果。当网格数达到500万左右时，离心风机全压和效率保持稳定，最终确定叶轮域网格数为510万，整机网格数达780万，仿生叶轮模型网格参数与原型相同。

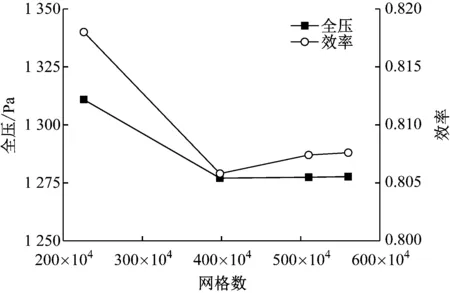
(a) 网格无关性检验

(b) 全压计算值与实验值的对比

图4(b)给出了原型风机全压实验值与计算值的对比，在0.6qV下定常计算值与实验值相差最大，相对误差为4.3%，且随着体积流量增大至1.2qV，二者间相对误差骤减至0.94%，离心风机在小体积流量工况下会表现出不稳定的工作特性[14]，因此，小体积流量下用定常计算值来衡量离心风机气动性能会造成一定误差，而小体积流量下全压的非定常计算值与实验值更贴近，整体趋势上也与实验值更相符，两者间的最大相对误差只有1.79%。综上，所采用的数值计算方法适用于离心风机的模拟计算。

2 计算结果分析

2.1 仿生叶片对离心风机气动性能的影响

图5给出了仿生离心风机的气动性能。由图5(a)可知，在小体积流量工况下，除锯齿尾缘改型外，表面凹坑、波形前缘结构均提升了离心风机的全压；设计工况下，表面凹坑型风机全压最高，高出原型56 Pa；在大体积流量工况下，波形前缘、表面凹坑结构增大了离心风机全压，其中表面凹坑型风机做功能力最强，全压较原型最大增大140 Pa。在整个体积流量范围内，表面凹坑结构对离心风机全压增大效果最明显，波形前缘型风机全压与原型相差不大但稍有提升(除设计工况外)，而锯齿尾缘结构反而减小了离心风机的做功能力。

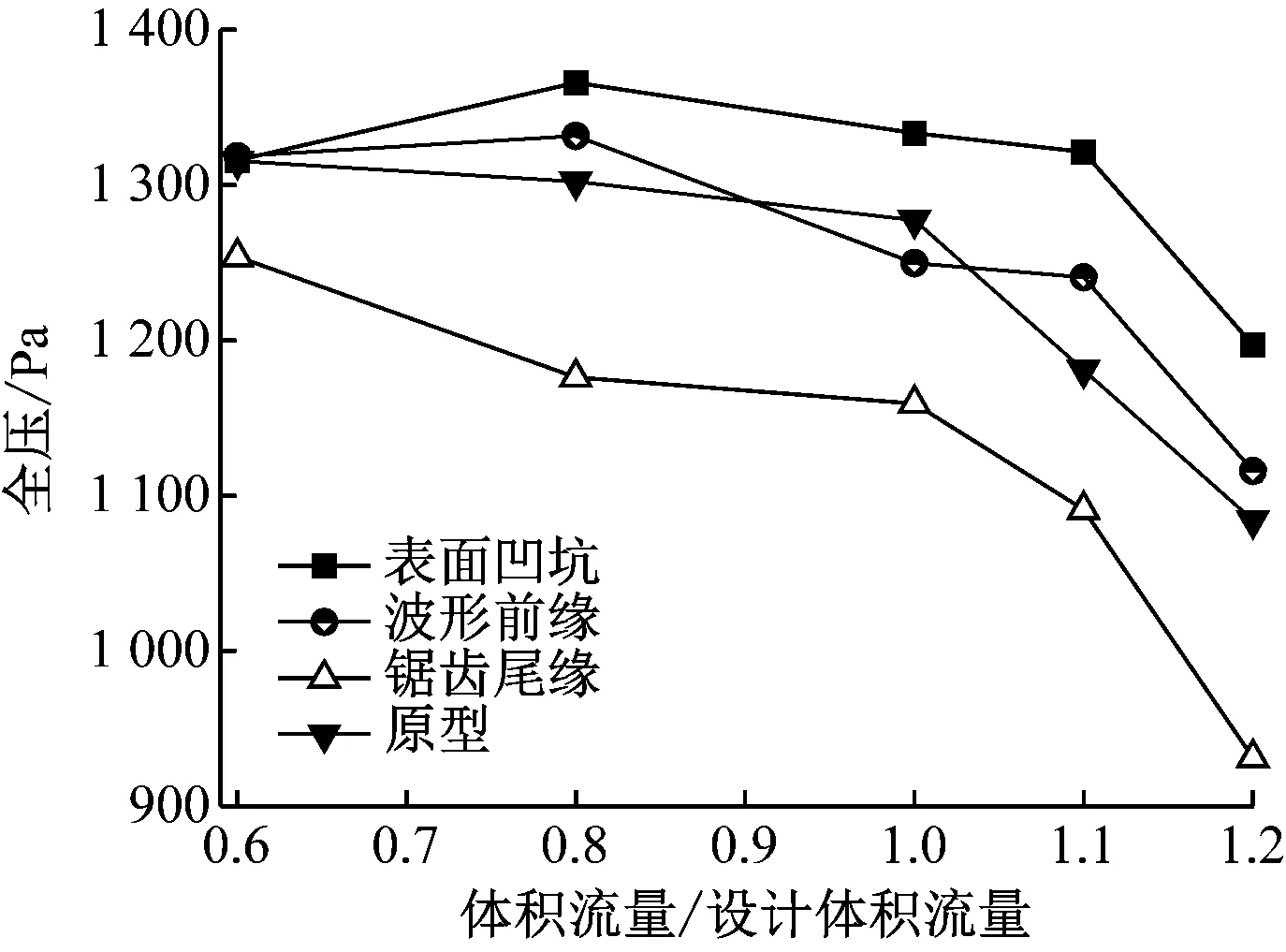
(a) 仿生离心风机全压曲线

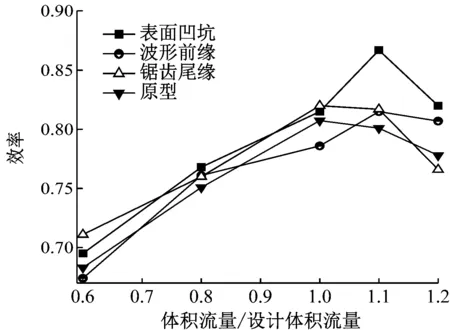
(b) 仿生离心风机效率曲线

图5(b)从效率角度对比了4种仿真离心风机的气动性能。随着体积流量的增大，效率呈现先升后降的趋势，不同的是，原型与锯齿尾缘型风机在qV下效率达到峰值，而表面凹坑型和波形前缘型风机却在1.1qV下效率最高。其中，4种离心风机效率峰值最高的是表面凹坑型，比原型高出6.6%。小体积流量工况下，锯齿尾缘和表面凹坑结构对离心风机效率有积极的影响，但当离心风机运行在大体积流量工况下时，这2种改型风机效率却急速下降，而另外2种改型风机效率降低缓慢。

综上，仿生结构对离心风机气动性能的影响有利有弊，这与仿生结构本身作用下的离心风机内部流场变化有关。锯齿尾缘型风机做功能力下降但效率不降，其原因是叶片尾缘切成锯齿状，减小了叶片的有效做功面积；波形前缘型风机气动性能与原型相差不大；表面凹坑型风机在全流量工况下的全压和效率始终高于原型，拓宽了离心风机的稳定工作范围，故将该仿生结构应用于离心风机时的气动性能最优。

2.2 仿生离心风机的流场分析

为揭示仿生离心风机内部流场规律及流动诱导下的气动噪声辐射特点，笔者分析了设计体积流量工况下4种离心风机的内部流场和辐射声场。

图6和图7给出了定常计算结果，由于该位置靠近轮盖，流体刚由静部件流入动部件，故在叶片吸力面上易产生流动分离，分离流堵塞流道，使叶轮通流能力下降。如图6(e)所示，分离涡在尾缘附近脱落，阻塞作用下气体未能从出口完全排出，在叶片前后表面间的压差作用下，上游尾迹流经下游流道出口，引起下游流动分离。

锯齿尾缘型风机叶轮内流线、湍动能分布与原型风机近似，分离区均位于涡舌前，流动状况的轻微改善使此工况下改型风机效率略高于原型；波形前缘型风机叶轮内更多流道发生分离现象，与原型相比分离区分布更广且跨过涡舌，这些位置对应于图7中的高湍动能区，大范围边界层分离、回流、分离流与主流掺混等过程消耗了部分轴功，使离心风机气动性能下降；表面凹坑型风机叶轮内分离区主要集中在涡舌后的流道，不存在漩涡占据整个流道的堵塞现象，叶轮通流能力增强，高湍动能区减少，流动稳定性增强，因此离心风机的全压和效率得到提升。

图8比较了4种离心风机瞬态计算结果，Q准则通过定义涡核等值面来反映叶轮内的三维涡分布。原型风机叶片吸力面上附着了大量涡结构，这些涡在流道内沿流向生成、发展和脱落。3种仿生手段皆减小了叶轮内的涡尺度，其中效果最佳的是表面凹坑型风机，除叶片压力面贴附一层薄薄的涡核外，流道内只分布着零星的点状小涡；其次是锯齿尾缘型风机，大涡被破碎成小涡，稀疏地散落在流道中；波形前缘结构是对叶轮内涡结构改善最不明显的仿生手段，相较原型只有部分流道得到调整。

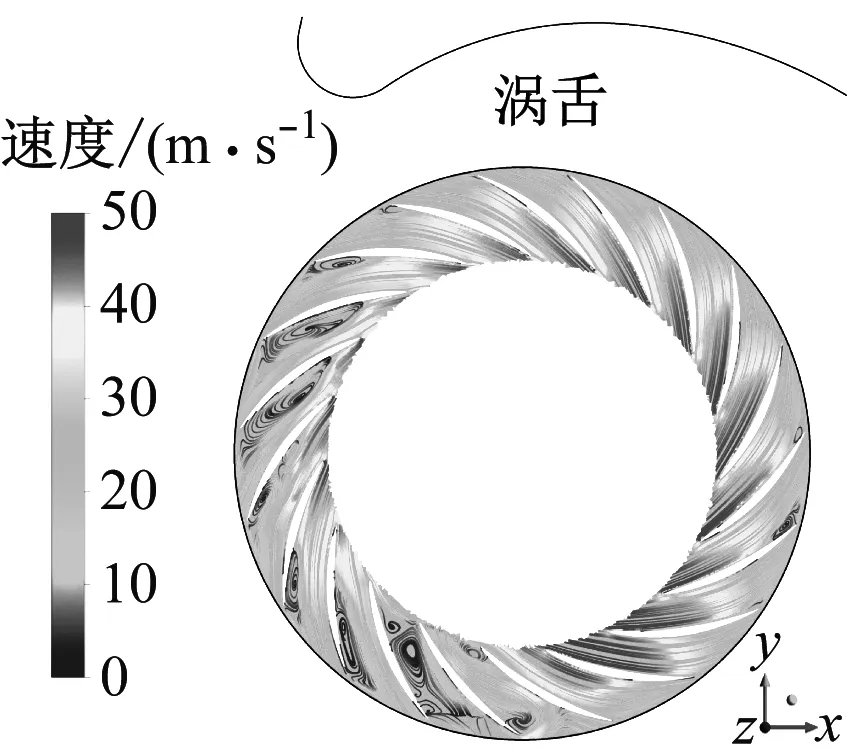
(a) 原型

(b) 锯齿尾缘

(d) 表面凹坑

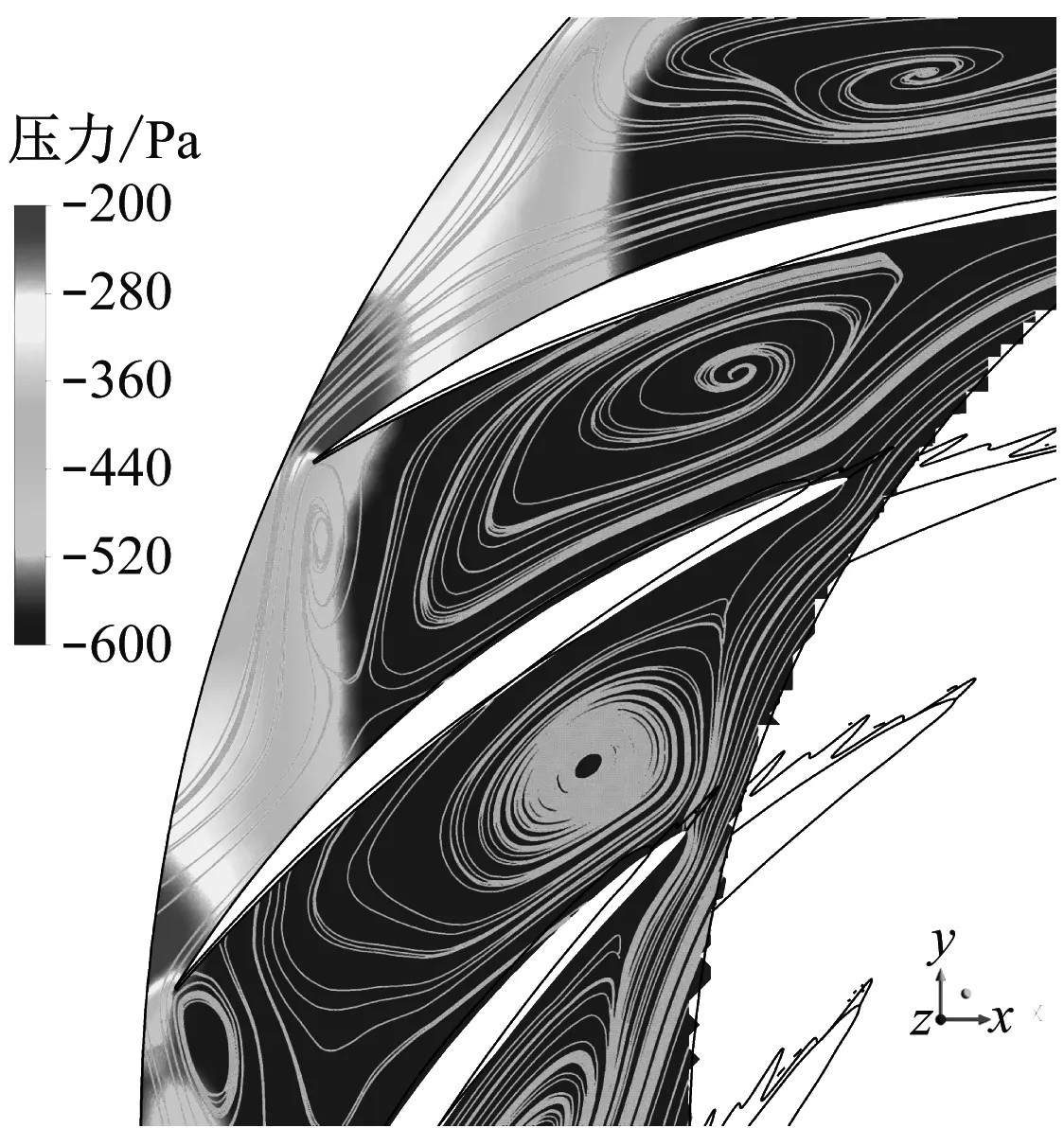
(e) 改型风机局部流道压力-流线分布(波形前缘)

(a) 原型

(b) 锯齿尾缘

(c) 波形前缘

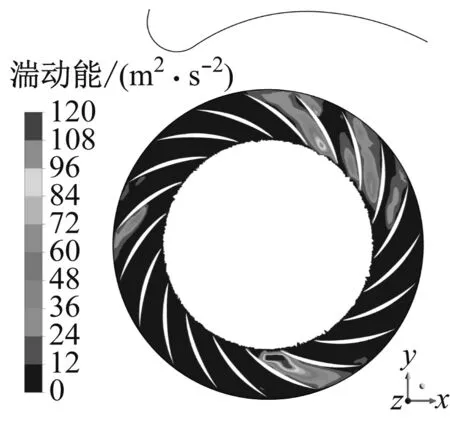
(d) 表面凹坑

(a) 原型

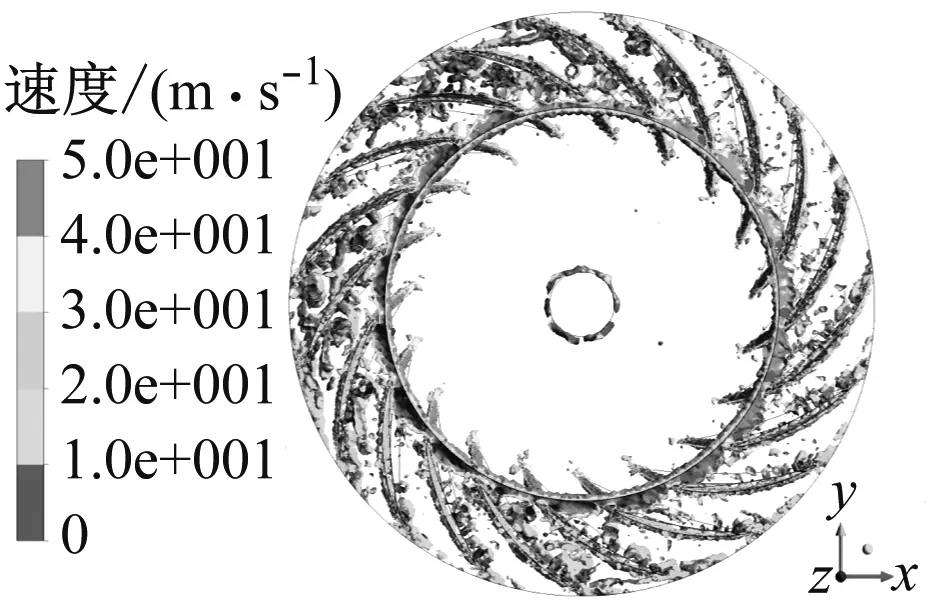
(b) 锯齿尾缘

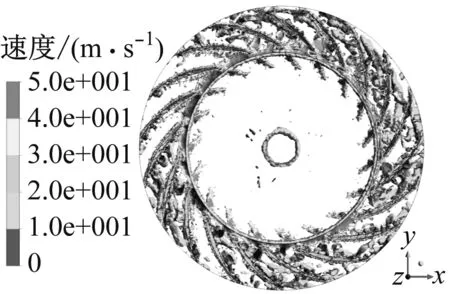
(c) 波形前缘

(d) 表面凹坑

在低马赫数下，可认为流动诱导噪声主要来源于涡[15]，由Powell涡声方程可知，涡量减小有利于降低低频下的流噪声，但大涡破碎成的小涡会在高频段增加噪声的贡献量。因此，各改型叶轮内涡核结构的调整将会削弱仿生离心风机辐射噪声的能力。

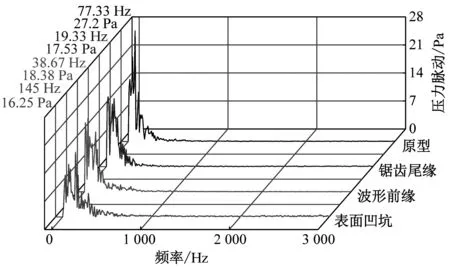
蜗壳作为主要声源面之一，需要考虑其内部流动。图9给出了蜗壳近壁处6个测点的压力脉动分布，每条曲线的脉动峰值及其对应频率在图中左上角给出。压力脉动主要贡献频率是1 000 Hz以下的低频段，由于所研究的原型风机涡舌与叶轮间隙较大，脉动主导频率不再是叶频(918 Hz)，而是由离心风机内部低频湍流信号引起的低频脉动，具体表现为4种风机压力脉动曲线主频皆小于150 Hz。靠近涡舌位置处(测点1和测点2)，压力脉动峰值除受低频信号影响外，还受轴频(48.3 Hz)及其倍频的影响。

由图9还可以发现，仿生离心风机在各测点上的脉动峰值频率与原型相比发生了偏移，而压力脉动主频对应于流场中的涡脱落频率，说明仿生结构改变了原型风机的内部流场，这一点在图8中得到验证。从整体上看，锯齿尾缘型、波形前缘型风机对压力脉动的控制较好，表面凹坑型风机在下游位置(测点4～测点6)具有抑制压力脉动的效果，但在涡舌附近(测点1～测点3)反而增大了压力脉动，这可能是改型叶轮出口与蜗壳间的不匹配造成的，不稳定流动增强了湍流与壁面的相互作用，从而使压力脉动增大。

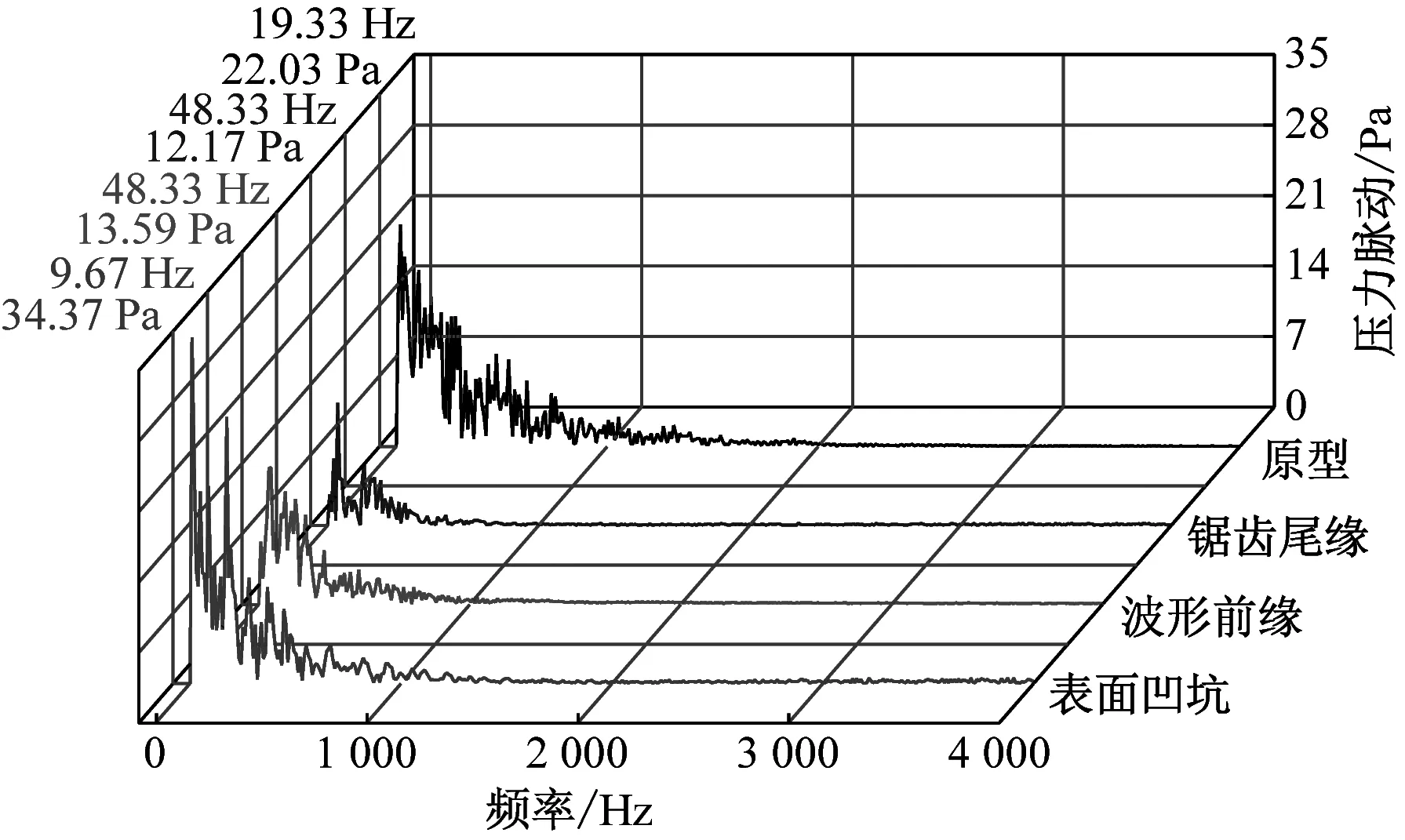
(a) 测点1

(b) 测点2

(c) 测点3

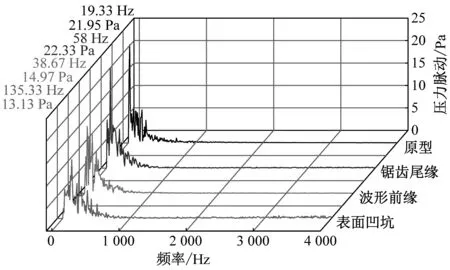
(d) 测点4

(e) 测点5

(d) 测点6

6个测点中，原型风机最大压力脉动峰值出现在测点5(27.2 Pa)，而锯齿尾缘型、波形前缘型、表面凹坑型风机最大压力脉动峰值分别出现在测点4(22.33 Pa)、测点6(18.55 Pa)和测点1(34.37 Pa)处。根据Lockard[16]和Casalino等[17]的研究结果：低马赫数下，流噪声主要呈偶极子特性，当偶极子源主导噪声时，压力脉动的削弱可降低偶极子声源。故可进一步推测锯齿尾缘型和波形前缘型风机具有一定的降噪效果。

2.3 仿生离心风机的声场分析

为研究仿生离心风机的声辐射特性，在位于叶轮出口50%叶高处的横截面上，距叶轮中心半径为1 m的环形一周共布置了24个声学远场测点(每隔15°布置1个)，各测点位置如图10所示。首先通过求解非定常流动控制方程得到离心风机流场数值解和声源压力信息；然后采用FW-H方法计算声源向远场辐射的噪声，即获得各测点上的声压级。

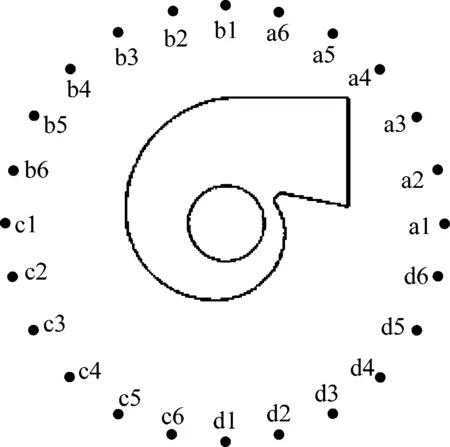
图10 声场测点位置分布

设计工况下的仿生离心风机声学对比如图11所示。仿生离心风机降噪效果对比如表1所示。4种仿生离心风机的声学指向性分布呈“多瓣”状，表面凹坑型、锯齿尾缘型风机在各接收点的总声压级均低于原型，其中降噪效果最好的是锯齿尾缘型风机，最大降噪量可达6.950 dB，平均降噪5.04 dB；波形前缘型风机降噪效果次之，平均降噪3.14 dB；表面凹坑型风机在大部分测点处总声压级略高于原型，噪声均值增大了0.85 dB。原型、表面凹坑型风机最大噪声接收点为d5，而锯齿尾缘型、波形前缘型风机则在d1测点处总声压级最大，4种风机均在c4测点处接收到的噪声最小。

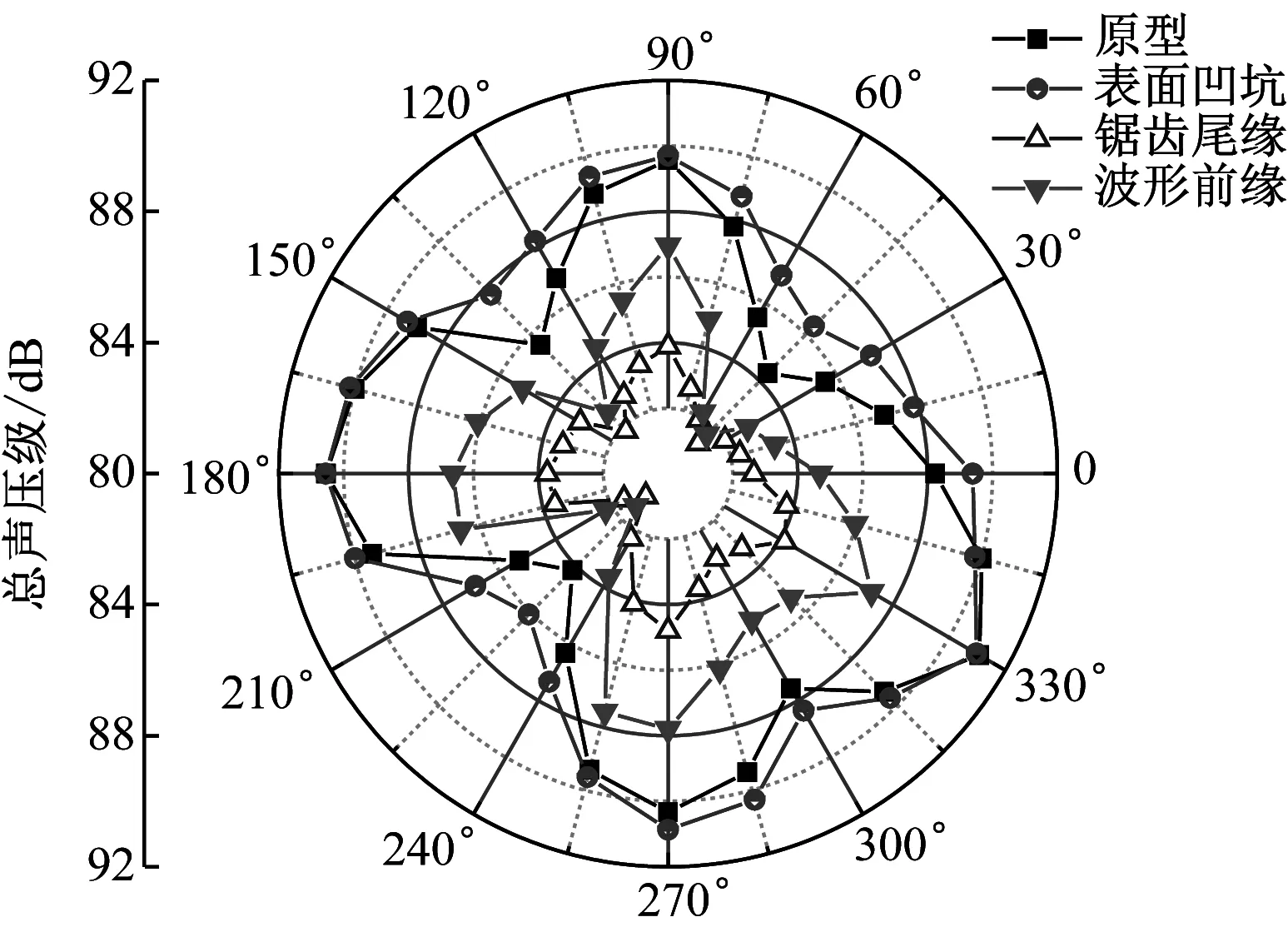
(a) 仿生离心风机的声学指向性分布

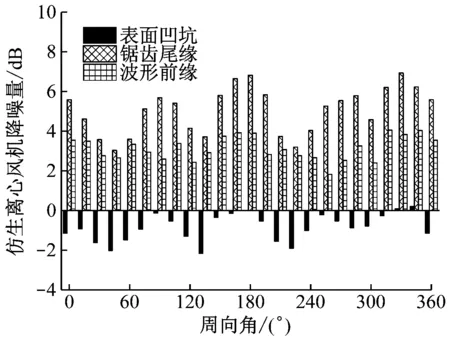
(b) 仿生离心风机降噪效果比较

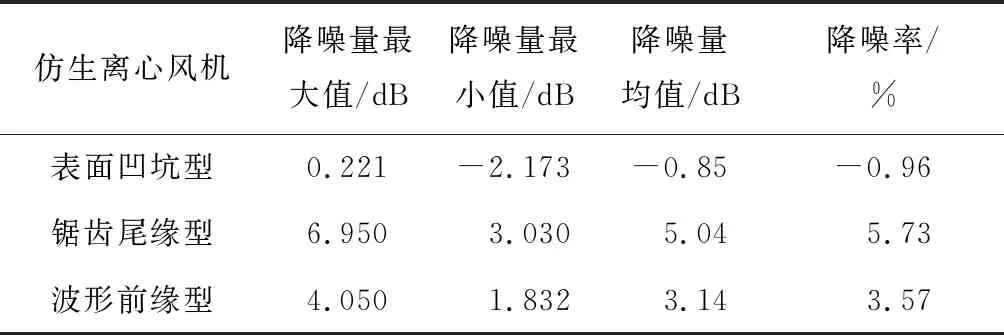
表1 仿生离心风机降噪效果对比

为进一步探究仿生离心风机的声场辐射规律，取离心风机最大噪声接收点d1、d5记录的声场信息做声压级频谱图。由图12可知，在轴频(48.3 Hz)处，原型、锯齿尾缘型和波形前缘型风机均出现了窄带单峰噪声，由于表面凹坑型风机可明显抑制叶轮流道内的涡脱落结构，故限制了离心风机在低频下的离散噪声。3种仿生结构在低频段均会给离心风机带来降噪效果，其中表面凹坑型结构的降噪效果最显著，该型离心风机总的降噪效果之所以不佳，是因为高频段的湍流宽频噪声增大所导致的；波形前缘型风机恰恰相反，高频段的低噪声贡献量使离心风机在d1、d5测点处拥有约3.4 dB的降噪量；锯齿尾缘型风机在整个频域内声压级都比原型低，所以最终表现出的声学性能最佳。

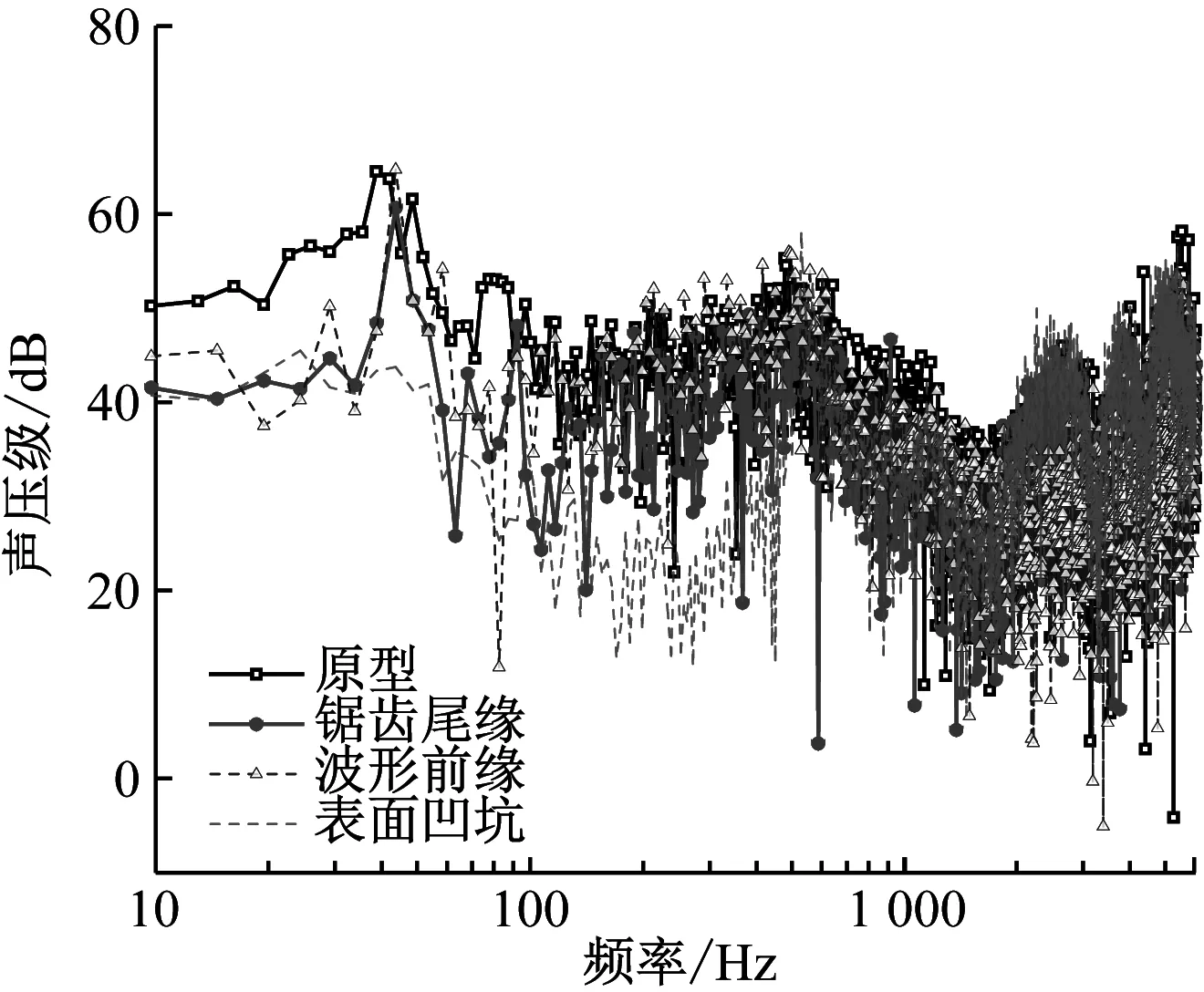
(a) d1测点

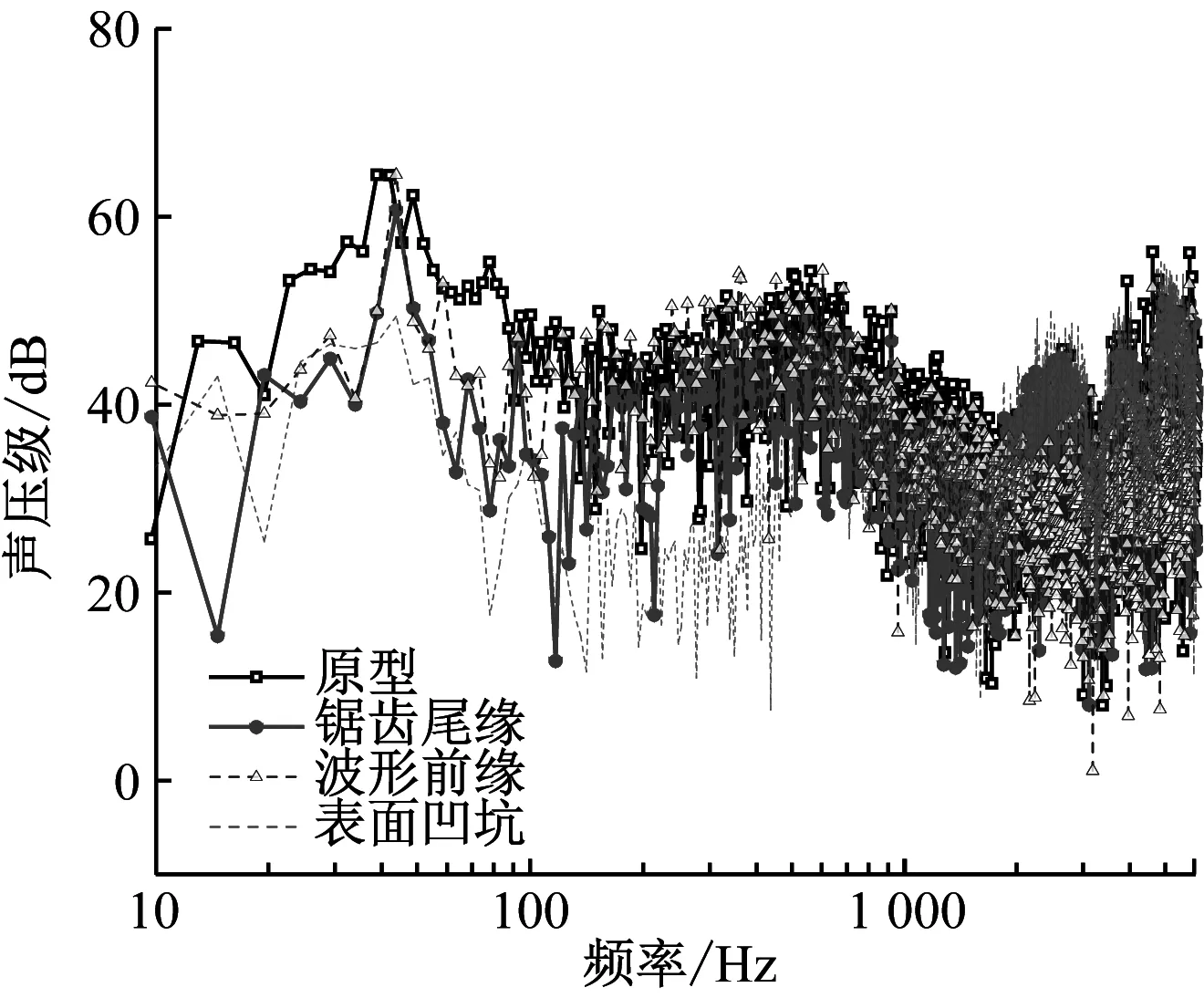
(b) d5测点

3 结 论

(1) 表面凹坑结构增大了离心风机的全压和效率；锯齿尾缘结构虽然减小了离心风机做功能力，却依然使离心风机在小体积流量工况下保持较高效率；波形前缘结构对离心风机的气动性能略有提升，但与原型相差不大。

(2) 设计工况下，3种仿生结构均可有效控制叶轮内的涡尺度，效果最佳的是表面凹坑结构，但此改型风机会增大涡舌处的压力脉动幅值(高出原型7 Pa)，另外2种仿生离心风机则抑制了蜗壳近壁处的压力脉动。涡量减小、压力脉动削弱有利于离心风机对噪声的控制。

(3) 设计工况下，波形前缘型、锯齿尾缘型风机的声学性能均优于原型，其中锯齿尾缘结构的降噪效果最明显，平均降噪量达5.04 dB；表面凹坑型风机虽然限制了轴频处的窄带单峰噪声，但高频段宽频噪声的贡献量增大，使得离心风机整体噪声不降反增0.85 dB。