基于PCA-MEA-WNN模型的燃烧不稳定性检测方法

黄 伟， 李常伟， 席建忠

(1.上海电力大学 自动化工程学院，上海 200090； 2.杭州华电江东热电有限公司，杭州 310000)

在我国环保事业中，燃气轮机的污染排放一直是一个难题。其排放物中对环境影响较大的是氮氧化物[1](NOx)，影响NOx排放的主要因素有燃烧方式、燃烧温度、燃烧室工况和燃料特性等[2]。基于污染排放问题，众多学者研发了许多先进的燃烧方式[3]，其中预混燃烧方式[4]是三菱M701F4型燃气轮机采用的燃烧方式。但预混燃烧方式的燃烧稳定范围太窄，很难满足燃气轮机在大范围变工况下运行的需求。燃烧不稳定性[5]主要表现为燃烧室内低频高振幅的压力振动，一旦发生燃烧振动，将会危及设备的安全运行，造成巨大的经济损失，所以对燃烧不稳定性进行检测和研究很有必要。

燃料在燃烧室高温燃烧，并生成高温燃气，然后在透平中膨胀做功，工作环境较为恶劣，燃烧温度过高，结构复杂，涉及的工况参数较多，数据难以获取，且不同工况下的燃烧过程容易受到扰动，对燃烧不稳定性的检测研究也较少。卓增泗等[6]采用小波变换多尺度分析对燃烧压力信号进行分解和重构，然后在时域和频域上分析燃烧压力信号，可以检测出燃烧不稳定性，但影响燃烧压力的因素较多，因而单纯观察燃烧压力的变化是不够全面的。叶家良等[7]基于现场可编辑逻辑门阵列硬件平台对燃气轮机燃烧过程的运行状况进行实时在线监控，虽然能够实现实时采集与分析，但是缺少真实数据结果的支撑。刘春霞等[8]提出了基于遗传算法优化小波神经网络(WNN)的天然气负荷预测模型，达到了优化小波神经网络阈值和连接权值的目的。谢克明等[9]通过建立的思维进化算法(MEA)的数列模型证明了此算法的全局收敛性。

综上所述，小波分析较傅里叶变换处理非线性问题较优，可以在时域和频域上进行分析，思维进化算法具有全局寻优的能力。为防止出现“过拟合”，笔者先采用皮尔逊相关系数对从传感器得到的大量数据进行相关性分析，然后根据准则选取相应的参数，并通过主元分析法(PCA)降维后提取出特征参数。根据各工况参数建立小波神经网络框架，采用思维进化算法优化小波神经网络的权值和阈值，再对燃烧压力进行检测。

1 燃烧不稳定性原理分析

研究对象为三菱M701F4型燃气轮机，其干式低NOx(Dry Low NOx, DLN)燃烧室有20个，每个燃烧室由8个预混主燃料喷嘴和1个值班燃料喷嘴组成，燃气轮机还有2个点火器和4个火焰监测器等，结构如图1所示，主要包括预混主燃料喷嘴、值班燃料喷嘴、燃气温度控制阀、燃气加热器、压气机进口导叶(IGV)控制阀和旁路阀等[10]。

图1 M701F4型燃气轮机的燃烧室结构

图2为发生燃烧不稳定性[11]的过程简图。如果燃料和空气供应不稳定，在两者混合、流动过程中燃料空气当量比发生变化以及漩涡脱落等因素都会造成速度和热力学状态的波动，引起燃烧放热振荡，从而激起声压模式的波动，反过来声压波动也会影响燃烧放热振荡和热力学参数，形成一个封闭的反馈环。

图2 不稳定燃烧过程简图

从燃料与空气混合、流动不稳定到出现燃烧不稳定性之间存在延迟，延迟时间为燃烧放热振荡特征时间t1,而声压波动也存在固有时间t2,t2主要取决于燃烧室的几何结构和温度分布[12]。根据瑞利准则，当t1等于t2或其整数倍，且燃烧放热振荡与声压波动同相位或近相位时，燃烧放热振荡对声压波动起到驱动作用。此时一旦燃烧放热振荡传递给声压波动的能量大于自身衰减时，声压波动能量不断升高，振幅随之增大，两者相互激发，最终产生燃烧不稳定性，导致低频、高振幅的压力波动。

三菱M701F4型燃气轮机燃烧室压力波动大时一般会出现以下现象：(1) 当24个传感器(即20个压力传感器和4个加速度传感器)中任何一个传感器压力值高于预报警设定值时，透平控制系统(TCS)发出报警；(2) 当燃气轮机在60%以上负荷运行，24个传感器中有2个传感器的压力值超过快速降负荷设定值时，燃气轮机快速减负荷；(3) 如果燃气轮机降低到负荷设定值以下后仍持续报警并超过设定的时间，燃气轮机跳闸；(4) 当其中2个传感器的压力值达到跳闸设定值时，燃气轮机跳闸。

2 MEA-WNN神经网络

2.1 主元分析法

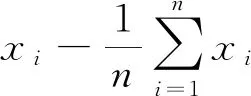
2.2 小波神经网络

小波神经网络是一种以BP神经网络拓扑结构为基础，信号前向传播、误差反向传播的神经网络。其实质是将BP的激活函数替换成小波函数，输入层到隐含层的权值及激活阈值由小波函数的尺度伸缩因子和时间平移因子代替。小波神经网络的拓扑结构如图3所示。

图3 小波神经网络拓扑结构

图3中向量X=(X1,X2,…,Xk)为输入，向量Y=(Y1,…,Ym)为输出；wij、wjk分别为输入层到隐含层、隐含层到输出层的权值。采用的小波函数为Morlet母小波函数，数学公式为：

(1)

式中:y为输出;x为变量。

训练过程如下：

(1) 网络初始化。

初始化小波函数尺度伸缩因子aj,时间平移因子bj以及权值wij、wjk，设置网络学习速率η。

(2) 隐含层输出。

(2)

式中：h(j)为隐含层第j个节点输出值；l为隐含层节点数；hj为小波函数。

(3) 预测输出。

(3)

式中：m为输出层节点数；y(k)为预测输出。

(4) 网络预测误差。

(4)

式中：yn(k)为期望输出；e为网络预测误差。

根据e修正网络权值和小波参数

(5)

(6)

(7)

式中：wn,i,k为网络权值；ai,k和bi,k为小波参数。

(5) 判断算法是否结束，若没有结束，则返回步骤(3)。

2.3 MEA-WNN

2.3.1 思维进化算法

思维进化算法主要由群体和子群体、公告板、趋同和异化组成，遗传算法中的交叉和变异算子具有双重性，可能产生好的基因也可能破坏原有的基因，而思维进化算法中的趋同和异化可以避免这个问题。思维进化算法的系统结构如图4所示。

图4 思维进化算法系统结构图

思维进化算法的基本思路如下：(1) 解空间内随机生成一定规模个体，根据得分搜索出得分最高的若干优胜个体和临时个体；(2) 分别以这些优胜个体和临时个体为中心，在每个个体的周围产生一些新的个体，从而得到若干优胜子群体和临时子群体；(3) 在各个子群体内部执行趋同操作，直至该子群体成熟，并以该子群体中最优个体的得分作为该子群体的得分；(4) 子群体成熟后，将各个子群体的得分张贴在全局公告板上，子群体之间执行异化操作，完成优胜子群体和临时子群体的替换、废弃、子群体中个体释放的过程，从而计算全局最优个体及得分。

2.3.2 MEA优化小波神经网络

思维进化算法优化小波神经网络之后,需要根据观测数据和预测数据计算两者的偏离度,再计算预警阈值,据此达到超限报警的目的。

(1) 计算偏离度来判断燃烧压力是否异常。

燃烧压力若正常，不进行诊断；若异常，则进一步融合燃烧室的各种工况参数进行决策分析，从而诊断燃烧室的运行状态。

引入偏离度r：

(8)

式中：q为拟合数据；u为观测数据。

偏离度越大越可能产生不稳定燃烧，偏离度逼近于0则表示燃烧室不会发生不稳定燃烧。

(2) 预警阈值设置。

设置的预警阈值是否合适直接影响到预警的效果，滑动窗口法不仅可以循环覆盖所有数据，且能通过已有的计算结果对搜索空间进行剪枝，大大减少重复计算，降低时间复杂度，故选择滑动窗口法设置预警阈值。

在滑动过程中，计算不同宽度窗口的偏离度均值E，以确立不稳定燃烧的预警阈值PAN。

(9)

式中：N为滑动窗口的宽度。

燃烧稳定范围的偏离度均值最大值记为EN，则预警阈值为：

PAN=gEN

(10)

式中：g为预警阈值的系数，根据电厂人员的经验获得，一般情况下取0.95。

(3) 优化过程。

PCA-MEA-WNN算法的流程如图5所示，PCA-MEA-WNN模型的网络结构采用4-5-1，并引入4个评价指标。小波神经网络权值参数修正采取梯度下降法，存在初始值敏感和易陷入局部极小的缺陷，针对此问题，使用思维进化算法对小波神经网络的权值和阈值进行优化。

优化的主要过程如下：

1) 划分训练集和测试集。思维进化算法利用种群产生函数产生初始种群和子种群，并划分训练集和测试集。

2) 编码。

将小波神经网络的解空间映射到编码空间，每个编码对应1个解。编码长度为s=s1×s2+s2×s3+s2+s3。前s1×s2个编码对应输入层到隐含层的权值W1；接着的s2×s3个编码对应隐含层到输出层的权值W2；s2个编码对应隐含层阈值B1；s3个编码对应输出层阈值B2。s1、s2和s3分别为输入层神经元个数、隐含层神经元个数和输出层神经元个数。

图5 PCA-MEA-WNN算法的设计步骤流程图

3) 各个子种群执行趋同操作，并利用种群成熟判别函数判断各个子种群是否完成趋同操作，若完成则执行异化操作。

4) 计算思维进化算法迭代过程中期望输出与迭代输出的均方误差SE和得分Val。

SE=mse(T-A2)

(11)

Val=1/SE

(12)

式中：T为期望输出；A2为迭代输出。

5) 解析最优个体。

若满足迭代停止条件，思维进化算法优化过程结束。根据编码规则，解析最优个体，从而得到对应的小波神经网络权值和阈值，再通过预测分析可以得到预测结果和相关指标。

3 实例分析

3.1 部分特征量分析

燃烧室的工作状态直接影响燃气轮机机组整体的运行，一旦燃烧不稳定，产生的高温烟气做功能力不足，会影响发电机发电，所以燃气轮机发电功率应作为一个参考特征量。由燃烧不稳定性原理可知，热释放率与声压互相影响，故选择火检信号作为一个参考特征量。

3.2 数据预处理

清洗数据后，得到17种相关工况参数。每种工况参数都包含一定信息，但不可避免会存在多重共线性，导致信息重叠。因此，需要对数据进行预处理，根据皮尔逊规则得到各参数与燃烧压力的相关系数，结果如表1所示。

相关系数ρC,D计算公式如下：

(13)

式中：cov(C,D)为协方差；σC和σD分别为C和D的标准差。

表1 皮尔逊相关性

根据皮尔逊规则选取相关系数较大的压气机效率、压气机压比、燃气透平膨胀比、燃气透平出力、火检信号1、火检信号2、火检信号3、火检信号4、IGV开度、压气机出口温度和发电功率作为降维输入参数。

利用SPSS软件进行PCA数据降维，在分析之前验证其可适性，对上述数据进行KMO检验和球形度检验，KMO检验结果为0.828，大于阈值0.5，符合要求。球形度检验的结果为0，小于0.05，将上述得到的工况参数排序后再采用PCA数据降维，并以累计贡献率为选取准则，结果表明发电功率、IGV开度、压气机出口温度和火检信号1 4个主成分的累计贡献率达到95%，最终选取这些参数作为小波神经网络的输入。

3.3 评价指标

对PCA-MEA-WNN模型进行性能评价，选取BP神经网络、小波神经网络和MEA-WNN神经网络的误差平方和(SSE)、决定系数(R2)、均方误差(MSE)和平均绝对误差(MAE)作为评价指标，计算公式如下：

(14)

3.4 结果与分析

3.4.1 燃气-蒸汽联合循环发电机组仿真平台验证PCA-MEA-WNN模型的性能

采用Matlab软件建立PCA-MEA-WNN模型，分别采取BP神经网络算法、小波神经网络算法和MEA-WNN算法进行计算，3种算法的结果如图6所示。

图6 3种算法的结果对比

由图6可知，在数据没有预处理的情况下，直接运用BP神经网络算法预测时，BP神经网络的预测效果不理想，对波动信号的拟合度不高。在进行相关性分析和数据降维后用小波神经网络算法预测，PCA-MEA-WNN模型输入发电功率、IGV开度、压气机出口温度和火检信号1，结果显示小波神经网络算法的预测误差呈收敛状态，较BP神经网络算法有所优化。而PCA-MEA-WNN算法的精度很高，预测误差接近0。

3种算法的各项评价指标见表2。

由图6还可知，各算法都能反映出燃烧压力的变化趋势，但是PCA-MEA-WNN算法的拟合效果明显优于其他算法。同时，表2中该算法的决定系数更逼近1，表明PCA-MEA-WNN算法的拟合度更高。对于SSE、MSE和MAE等评价指标，PCA-

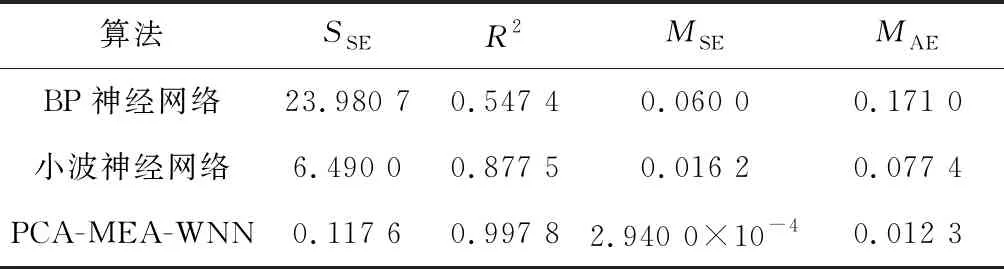
表2 不同算法的性能对比

MEA-WNN算法得到的结果均小于其他算法，即PCA-MEA-WNN算法对燃烧压力的预测精度更高。

3.4.2 电厂实际运行分析

已知电厂的发电机组出现不稳定燃烧，随着燃气轮机负荷的提升，不稳定燃烧越来越明显。因此，选取出现不稳定燃烧前的正常数据作为训练数据，之后的数据作为观测数据。用Matlab软件画出燃烧压力的趋势曲线，如图7所示。

图7 原始信号波形

数据清洗后，选择某电厂2019-05-12 T 06：24：00-06：47：00中的前600个数据进行相关性分析和降维处理，然后作为PCA-MEA-WNN模型的输入，进行拟合预测。将燃烧压力信号第701到第1 500的数据作为观测数据，通过拟合结果和观测数据来计算偏离度，设置阈值后进行分析。

利用PCA-MEA-WNN模型分析燃烧压力信号，预测结果如图8所示。由图8可知，此模型能够预测稳定燃烧时压力的变化趋势，但是在捕捉实际发生的燃烧不稳定性的过程中存在欠缺，所以通过分析燃烧压力的波动来间接反映燃烧不稳定性有些牵强。其原因如下：

图8 PCA-MEA-WNN模型拟合结果对比

(1) 从数据出发，燃烧室的工作环境恶劣，涉及的工况参数较多，且各参数都伴随着物理变化和化学变化，因此数据随机性太强，学习难度较大，即输入与输出之间关系映射的随机性太强，即便历史数据有一定的参考意义，但随机性大于数据内部规律，只凭数据很难做到精确的预测。

(2) 从原理出发，燃烧室内的环境极其恶劣，工况参数掺杂的噪声太多，对预测效果影响较大，单单获取数据便是一项难题。同时，涉及的工况参数较多，在对数据清洗以及预处理的过程中很容易遗漏信息。

(3) 从算法本身出发，虽然思维进化算法中的趋同和异化操作可以避免遗传算法双重性的缺点，但其种群规模、优胜子群体和临时子群体的个数对优化结果有一定影响。

根据以上分析，改进方向有：(1) 增加训练集和测试集样本；(2) 调整种群规模、优胜子群体和临时子群体的个数；(3) 为提高网络学习速率，增加动量项来修正权值和参数。

其中，增加动量项修正权值和参数的程序如下：

wij=wij-lr1×d_wij+f×(wij_1-wij_2);

wjk=wjk-lr1×d_wjk+f×(wjk_1-wjk_2);

b=b-lr2×d_b+f×(b_1-b_2);

a=a-lr2×d_a+f×(a_1-a_2)。

其中，f为动量项学习速率；w为修正的权值；a、b为修正的阈值；lr1和lr2分别为修正权值和阈值的学习速度；d表示增量。

种群大小为200，优胜子种群个数和临时子种群个数均设置为5，迭代次数为10。图9为优胜子种群和临时子种群的趋同过程。由图9可知，待种群成熟后发现临时子种群中的子种群2和子种群5的得分高于优胜子种群中子种群5的得分。因此，需要执行2次异化操作，同时补充2个新的子种群到临时子种群中。

改进后的对比结果如图10所示。由图10可知，燃烧压力幅值在第290 s处有上升趋势，随即快速增大，并且持续大幅度震荡，在第660 s处开始下降，然后趋于平缓。结合预混燃烧特性，在低负荷工况下燃烧温度较低，容易引发熄火，发生不稳定燃烧，结果与实际相符。上述燃气轮机平台的性能评价已经验证该模型具有很高的精度，所以当发生不稳定燃烧时，燃烧压力会发生较大偏离，但相对于残差该模型仍具有更好的观测效果。根据上述结果计算得到的偏离度如图11所示。

(a) 初始优胜子种群趋同过程

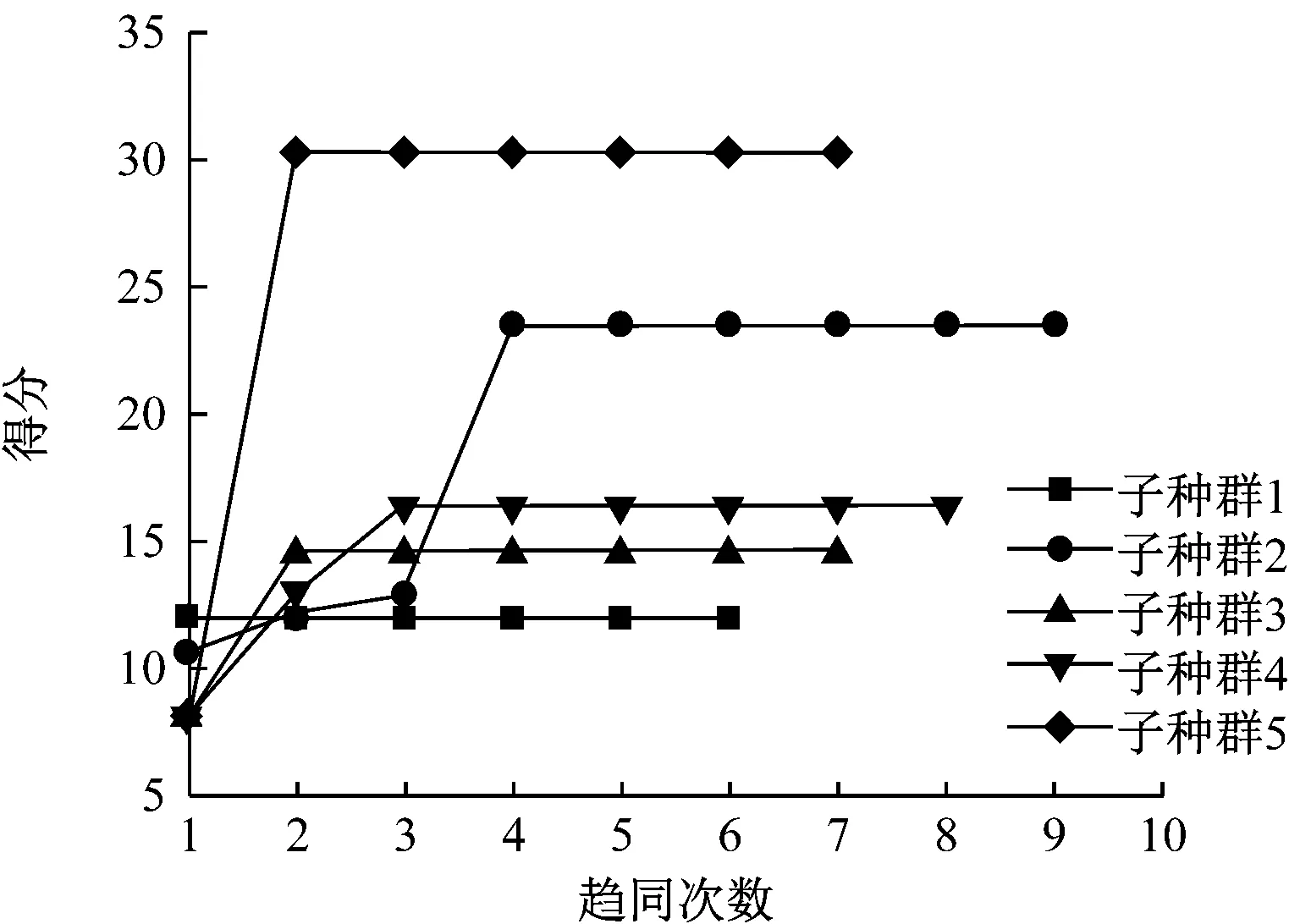
(b) 临时子种群趋同过程

图10 PCA-MEA-WNN算法得到的燃烧压力幅值

由图11可知，在第344 s之前偏离度有上升趋势，并在该处偏离度突增，然后保持较大幅值的震荡。由此可知，偏离度的变化可随时灵敏地反映燃烧的动态变化，不仅可以检测到燃烧压力异常的情况，而且可以更早地发现异常。

图11 燃烧压力预测值与观测值的偏离度

选择滑动窗口的宽度N为38，在图11中，根据式(9)可得EN=0.128 9,则预警阈值为PAN=0.122 455。

偏离度一旦超过0.122 455，会立刻发出报警信息以便后续诊断和调整。在第344 s便发出报警信息，即在不稳定燃烧初期便发出报警，对工作人员及时处理异常情况有很大的帮助。

综上所述，PCA-MEA-WNN模型对于燃烧室燃烧压力的异常检测具有很好的效果。

4 结 论

(1) 在处理非线性、复杂问题上，相较于BP神经网络算法和小波神经网络算法，PCA-MEA-WNN算法有更优异的效果。

(2) PCA-MEA-WNN模型具有更为快速的网络学习速率和较高的逼近能力，提高了燃烧压力的拟合精度。

(3) PCA-MEA-WNN模型的精度很高，但是计算量也增加，利用偏离度可以更灵敏地监测燃烧压力信号的动态变化，不仅可以检测出燃烧异常，而且可以在燃烧异常的初期便发出报警信息，大大减小了发生故障的可能性。