浆水平衡计算分析和难点解决

夏松珂，吴晨曦

（1.中国轻工业长沙工程有限公司，长沙 410114；2.东莞市金田纸业有限公司，东莞 523039）

物料平衡计算是工艺设计工作中至关重要的内容。其重要性主要体现在3个方面：（1）是工艺生产过程中一切计算的基础，用来确定工厂生产线的设计能力和规模，为工艺设计和经济评价提供基本依据[1]；（2）为工艺流程设计、设备选型和配管设计提供依据；（3）为生产改进、成本降低和节能减排提供依据。

物料平衡计算过程遵循质量守恒定律。就造纸工业而言，物料平衡计算包括蒸煮、洗涤、漂白、造纸等生产过程中的浆水平衡计算，还包括碱回收生产过程中的碱平衡计算。其中，浆水平衡是制浆造纸工程中应用最广泛和最重要的内容。

浆水平衡是一种特定的物料衡算形式，其内容为：进入某衡算体绝干浆和水的总量等于离开该衡算体的绝干浆和水的总量[2]。该衡算体可以是一个工艺设备、一个系统或一个工段，还可以是一个节点，如浆流汇合点或分支点。

1 浆水平衡计算分析

1.1 步骤

通常，浆水平衡计算工作可以分为5步：确定流程方框图，设定工艺参数，具体计算，制作浆水平衡明细表，绘制浆水平衡方框图。本文旨在分析浆水平衡具体计算的细节、难点及实现自动求解，上述其他步骤不再赘述。

1.2 限定条件

在具体计算前，首先要分析浆水平衡原理，然后根据其物理过程抽象出数学算式(即数学模型)，最后通过数学工具求解。通过对浆水平衡过程的分析发现，该过程具有以下3类限定条件：

第1类条件是质量守恒，即对于任一衡算体，浆料流股中的绝干浆量与进出总流量守恒[2]。

绝干浆量守恒的方程式为

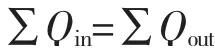
进出浆料的总流量守恒的方程式为

式中：Qin为进入衡算体某流股中的绝干浆量；Qout为离开衡算体某流股中的绝干浆量；Vin为进入衡算体某流股的浆料体积；Vout为离开衡算体某流股的浆料体积。

第2类条件，流股中绝干浆量等于流股的浆料浓度与体积的乘积，即对于任一浆料流股都满足限定条件

式中：Q为浆料流股中的绝干浆量；C为浆料流股的浓度；V为浆料流股的体积。此类条件表明，任一浆料流股中的3个变量（绝干浆量Q，体积V和浓度C）的自由度只有2，在Q、C和V这3个参数中只要确定了其中2个，那么第3个参数也就随即被确定了。

利用这一关系，在选择未知变量和列计算方程时就可以有针对性地进行选择。例如，在列方程时不要让未知变量V与未知变量C的乘积出现方程中。这样得到的方程式始终是线性方程，利用简单代数运算便可求解；否则，在方程组中会有非线性方程出现[3]，导致求解计算的复杂程度大大增加。

第3类条件，浆料分配比率Rij满足

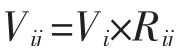
式中：下标i表示第i流股，ij表示第i流股的第j分支。参数Rij可以是浆处理设备的排渣率、分支管路的回流比、分级筛的长短纤维分配比例等。作为一个已知参数，其对平衡计算中流股之间的数学关系起到约束作用。

1.3 方程组求解

根据上述限定条件，可以对进出衡算体流股列出若干数学方程式，得到一个方程组，进而求解。由于之前在设定参数时的简化工作，每个方程式中未知数的幂次均为1，所以接下来面对的是线性方程组求解工作。

对于一个由n个方程式组成、包含m个未知数的线性方程组，方程组系数矩阵的秩为r，该方程组的解有如下3种情况：

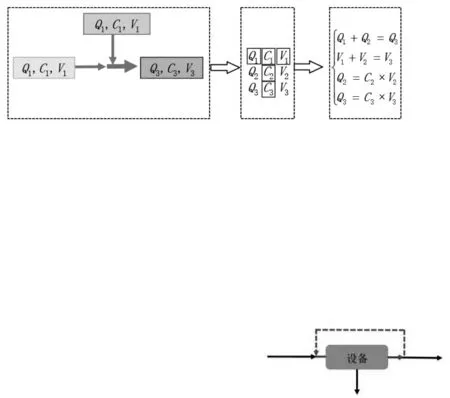
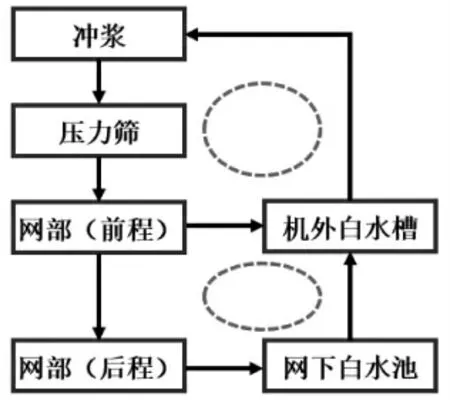
（1）如果r

（2）如果r=m，则此线性方程组有唯一解；

（3）如果r>m，则此线性方程组无解。

根据制浆造纸工艺要求，浆水平衡计算的结果只能是唯一的，即要求方程组有唯一解。

然而，在繁琐的计算过程中经常容易出现违背上述条件的错误，比如在对某除砂器进行平衡计算时，同时设定了排渣率R和全部浆料流股浓度C，导致了方程组无解。因此需要仔细检查，避免此类情况发生。

1.4 过程总结

浆水平衡的具体计算过程，不仅仅是数学计算过程，还需要满足实际需要。以一个调浓节点为例，其浆水平衡计算过程如图1所示。计算过程可归纳为3个步骤，图1中每个虚线框代表其中一步，其中第2步“参数分析”中带实线边框的参数为已知参数，其他为未知参数。

图1 浆水平衡计算基本过程

首先，把调浓节点作为一个衡算体，通过对该衡算体的分析可知，有两个流股进入衡算体，一个流股离开。然后，对每个流股中3个参数进行分析，区分其中的已知参数和未知参数。最后根据第1类和第2类限定条件列出方程组。

如上所述，浆水平衡计算是将现实问题归结为相应的数学问题，并在此基础上利用数学的概念、方法和理论进行深入的分析，从而从定量的角度来刻画实际问题，并为解决现实问题提供精确的数据或可靠的指导。

2 浆水平衡计算中的循环回用问题与求解困境

循环回用是制浆造纸工艺流程中非常普遍的现象，其基本类型可归纳为2类：一类是单台设备的循环回用，如高浓除砂器和双盘磨出口的浆料部分回流至设备进口；另一类是整个系统的循环回用，如白水回用。因此，带有循环回用系统的浆水平衡计算成为具体计算中的难点。

以高浓除砂器为例，经过处理的浆料流股中一部分回流至设备进口处，与上游浆料混合后一同进入该设备。这样循环回用过程形成了一个“闭环”，如图2虚线所示。

图2 浆水平衡计算过程中的闭环问题示意图

然而，对于这个简单的“闭环”现象，不能应用常用软件EXCEL实现自动计算。主要原因在于EXCEL不允许输入值作为输出值，否则就违反了EXCEL运行中所遵循数据流规则（即在所有数据都到达输入端时，节点才可以继续运行下去；并且数据不会在节点结束运行前到达输出端）。对于“闭环”情况，即输入端数据直接取决于输出端（回流）数据，同时输出端（回流）数据也直接取决于输入端数据时，输入端和输出端都无法完成计算，这成为了一个“死锁环”，即代数环问题（Algebraic Loop）。

对于由循环回用引起的代数环问题，在采用EXCEL计算时可用两种方式解决：（1）人为打断闭环，在起点处设定初值，然后根据计算结果不断调整设定的参数值，直至衡算结果达到平衡，这种方法执行起来比较麻烦，但可以解决绝大部分问题。（2）对闭环所涉及的平衡计算，通过变换法调整平衡计算公式，避免计算过程出现代数环问题，这种方法很难解决复杂的循环回用问题（如图3），并且当删减设备时的适用性差。

图3 浆水平衡计算中的典型复杂循环回用问题（“8”字循环）

3 计算工具的比较

常用的3种浆水平衡计算工具包括EXCEL、MATLAB Simulink和LabVIEW。

3.1 EXCEL

EXCEL是传统计算的常用工具。采用EXCEL软件进行平衡计算时，只要设置好计算公式，所有计算是自动进行的；当需要修改某个平衡计算参数时，只需要改动对应单元格的数值或公式即可，其他单元格的计算结果自动更新[2]。然而，EXCEL并不能完美解决浆水平衡计算中所有问题。存在的问题主要有两个[4]：（1）流程中若增加或减少设备，均需要重新分析、推导、求解物料守恒方程式，重新输入公式或引用；（2）对于循环回用的情况（如前所述），需要对某些流股进行初值设定，并根据其他单元格的计算结果多次手动调整设定值。

3.2 Simulink与LabVIEW仿真软件

Simulink是MATLAB软件中的一种模块图环境，是实现动态系统建模、仿真和分析的一个软件包。LabVIEW是一种图形化程序开发环境，产生的程序是框图的形式，使得编程及使用过程都很简便。基于Simulink仿真或LabVIEW仿真的浆水平衡计算基本上是采用3个步骤：分析设备模块需求与分类，建立设备模块，绘制仿真流程图。

与EXCEL相比，采用Simulink或LabVIEW仿真时的建模工作相对较简单，无需大量重复书写公式，增删设备时通常只需要复制设备模块并加入到仿真流程图中，就可以实现对工艺流程中的设备调整。在Simulink和LabVIEW仿真时，要解决循环回用引起的代数环问题，只需要在输出端与输入端之间放置一个延迟模块（Unit Delay）或反馈节点（Feedback Node）[4-5]，并进行赋初值即可，无需进行更多的调节或改动。这样通过在输入端赋初值（即回流流股参数赋初值），并经多次迭代后便可得到稳定数据，即解决了代数环问题。此外，LabVIEW仿真相对于Simulink仿真而言，具有对程序开发的要求更低和用户界面更友好等优势。

从用户界面的友好性、解决复杂问题的难度、计算维护的难易等方面综合考虑，浆水平衡计算采用LabVIEW仿真的优势最大，其次是Simulink，最后是EXCEL，具体见表1。

表1 三种计算工具的综合评价

3.3 模块化思路

在实际工艺流程中，通常在进除砂器前有一级调浓，包括一个调浓节点和一个除砂器设备的浆水平衡计算共需要对由9个方程构成的方程组求解。那么，对于含调浓节点的二段除砂器系统就需要求解由18个方程构成的方程组。而现代造纸企业的一条废纸处理浆线就有100台设备左右，为每台设备和分支点都推导计算公式的工作量是很大的。繁琐的计算工作不仅耗时、易出错，还存在调试和变更麻烦等问题。

在利用EXCEL进行浆水平衡计算时，要先求得方程组的代数解，然后才能在相应单元格中输入公式。然而，EXCEL也不是一直适用的，因为每个工程项目都不同，在项目进行的过程中，对流程方案的调整也时常发生，这些都会为EXCEL计算公式、引用单元格、公式检查带来很大的变更工作量。因此，就需要一种计算过程简化、移植性好的解决方案。

对于Simulink和LabVIEW仿真，可分别采用S-Function核心模块程序和虚拟设备程序（VI）建立模块化设备模型。在对共性的模块化设备进行浆水平衡计算时，只需要调用模块化设备模型并修改设备设计参数即可。这种思路与模块化的设计思路相符。纵观制浆造纸工艺流程，除了个别设备之外，绝大多数的衡算体都可视为“一进二出”、“二进一出”和“循环回用”这些模块的组合。利用模块进行调用，会极大降低编程的重复率和出错率。

4 结束语

随着中国造纸工业的发展，自主工艺设计在工程设计中的比重越来越高。本文结合在实际工程设计中的浆水平衡计算经验，对计算原理进行分析，并且寻找能方便解决流程设计难点“循环回用”问题的工具软件。通过分析对比可知，基于模块化思想的MATLAB Simulink和LabVIEW，更适于工艺设计人员进行浆水平衡计算。