基于曲面拟合的脉冲涡流测厚方法
王安泉,孙国健,孙 亮,郝宪锋,万 勇, 戴永寿
(1.中国石油化工股份有限公司胜利油田分公司技术检测中心,东营257000;2.中国石油大学(华东) 控制科学与工程学院,青岛 266580;3.中国石油大学(华东) 海洋与空间信息学院,青岛 266580)
脉冲涡流检测技术是一种采用具有一定占空比的方波电流为激励源的涡流检测技术[1-2]。由于方波具有频谱宽,包含信息丰富等特点,所以该技术能检测不同深度的缺陷,被广泛应用于承压设备以及带包覆层管道的缺陷检测中[3-4]。
针对带有包覆层的管道,采用脉冲涡流技术可以实现非拆除包覆层条件下的壁厚检测。但由于包覆层的存在,检测时传感器与管道之间存在较大提离,受提离效应的影响,检测信号幅值衰减严重,信噪比降低,特征量变化规律也随之改变,导致壁厚反演误差增大。
孙杰等[5]针对不同厚度包覆层的管道,给出多组检测电压幅值与金属壁厚的拟合曲线。吴月东等[6]提出了一种基于相对磁通量变化率的铁磁性材料脉冲涡流检测信号的提离效应消除方法。曲天阳[7]采用检测线圈测量的晚期斜率特征量以及采用霍尔元件测量的磁感应强度对提离造成的误差进行修正,减少了提离效应对检测结果的影响。石坤等[8]通过试验给出提离高度与误差之间的函数关系,并进行了定量分析,最后通过补偿函数对误差进行补偿。顾增涛等[9]采用带控制量的自回归模型的系统辨识方法来抑制提离效应。然而上述提离补偿方法存在反演模型复杂、反演精度低等问题,未能在现场检测中得到广泛应用。
笔者基于对晚期信号斜率特征量、提离高度以及管道壁厚三者关系的分析,提出了一种利用三维曲面拟合对提离效应进行修正的方法,并通过试验验证了该方法可用于带包覆层管道壁厚的检测。
1 脉冲涡流检测系统
脉冲涡流检测系统主要包括上位机、脉冲信号发生模块、功率放大模块、激励线圈、被测试件、检测线圈、放大滤波模块及数据采集模块等。另外,定制加工了2根管道阶梯试件,试件材料选用磁导率为400 H·m-1的Q235钢,每根试件有3个阶梯,共计6个阶梯,试件壁厚为4.512 mm。
脉冲涡流检测系统框图如图1所示,工作过程可描述为:利用上位机软件设置激励参数,下发命令控制脉冲信号发生模块产生一定幅度、频率及占空比的脉冲信号,脉冲信号经功率放大模块放大后加载到激励线圈两端,再由检测线圈检测叠加磁场的变化,并将其转换为电压信号,检测电压信号再经前置放大滤波模块后输入至数据采集模块,最后通过上位机读取采集模块的数据,并对其进行处理与分析。

图1 脉冲涡流检测系统框图
试验所用传感器由激励线圈、接收线圈、锰锌铁氧体磁芯以及线圈骨架等组成。采用的传感器激励线圈内径为9 mm,外径为30 mm,高度为40 mm,线圈匝数为800匝;接收线圈内径为32 mm,外径为40 mm,高度为12 mm,线圈匝数为1 200匝。
2 脉冲涡流检测信号及特征分析
2.1 特征量的提取
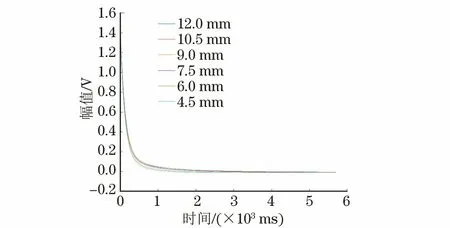
图2 不同壁厚管道的感应电压信号
脉冲涡流检测系统采集到的电压信号由二次磁场感应产生,图2为不同壁厚管道的感应电压信号,由图2可知,其晚期信号极其微弱,通常为毫伏级甚至微伏级,在笛卡尔坐标系中,信号曲线几乎重合在一起,难以区分。由于电压信号在短时间范围内发生了几个数量级的变化,所以将感应电压信号进行了单对数坐标转换(见图3)。由图3可知,在一段时间内,感应电压快速衰减,其中直线部分对应着涡流由试件上表面向下表面扩散的过程。根据趋肤效应[3],在这一过程中,涡流强度随深度呈指数规律衰减,涡流产生的磁场在检测线圈上感应出的电压也呈指数衰减[10]。
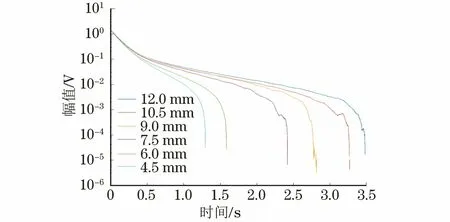
图3 单对数坐标系下不同壁厚管道的感应电压信号
在单对数坐标系下,随着时间的增加,不同壁厚的感应电压曲线的晚期斜率有了明显区分,由于图中的快速衰减部分对应着脉冲涡流能量从被测试件上表面到达被测试件下表面后的过程,所以涡流在不同壁厚试件上的衰减速度不同,衰减规律表现为:壁厚越大,信号衰减得越慢。由图3可知,感应电压信号晚期斜率与被测管道壁厚有着一一对应的关系,因此晚期信号斜率可以作为管道壁厚检测的特征量,以用来进行壁厚的反演。
综上可知,可以通过求取晚期斜率特征量,来计算管道壁厚。例如求解图3中6个不同壁厚管道的感应信号晚期斜率,可以得到晚期信号斜率与壁厚的对应关系(见表1),然后建立晚期信号斜率与壁厚之间的关系曲线(见图4)。

表1 晚期信号斜率与壁厚的关系

图4 晚期信号斜率-壁厚拟合曲线
以晚期信号斜率为自变量,以壁厚为因变量,利用幂函数y=a·(-x)b进行拟合,得到的函数关系如式(1)所示。
y=235.4·(-x)-0.660 3
(1)
为了验证此反演模型的精确度,重复检测上述6个不同壁厚的管道,求取对应的晚期信号斜率后,根据拟合公式求解反演壁厚,并计算反演的相对误差(见表2),由表2可知,壁厚反演误差在7%以内。

表2 壁厚拟合结果相对误差
2.2 带包覆层管道的检测信号特征分析
在涡流检测中,由于管道包覆层的存在,传感器与管道之间会存在较大提离。传感器和被测物体间高度的改变对涡流大小造成的影响称为提离效应。脉冲信号为直流分量和一系列不同频率正弦信号的叠加,因此可将提离效应看成提离对单一频率信号响应影响的叠加。图5为单一激励频率下的脉冲涡流检测等效电路[11],由基尔霍夫定律可知

(2)
式中:U为激励电压;f为激励信号频率;R1,L1,I1分别为激励线圈的电阻、电感和电流;R2,L2,I2分别为被测试件中感应的电阻、电感和电流;M为激励线圈与被测试件之间的互感系数。
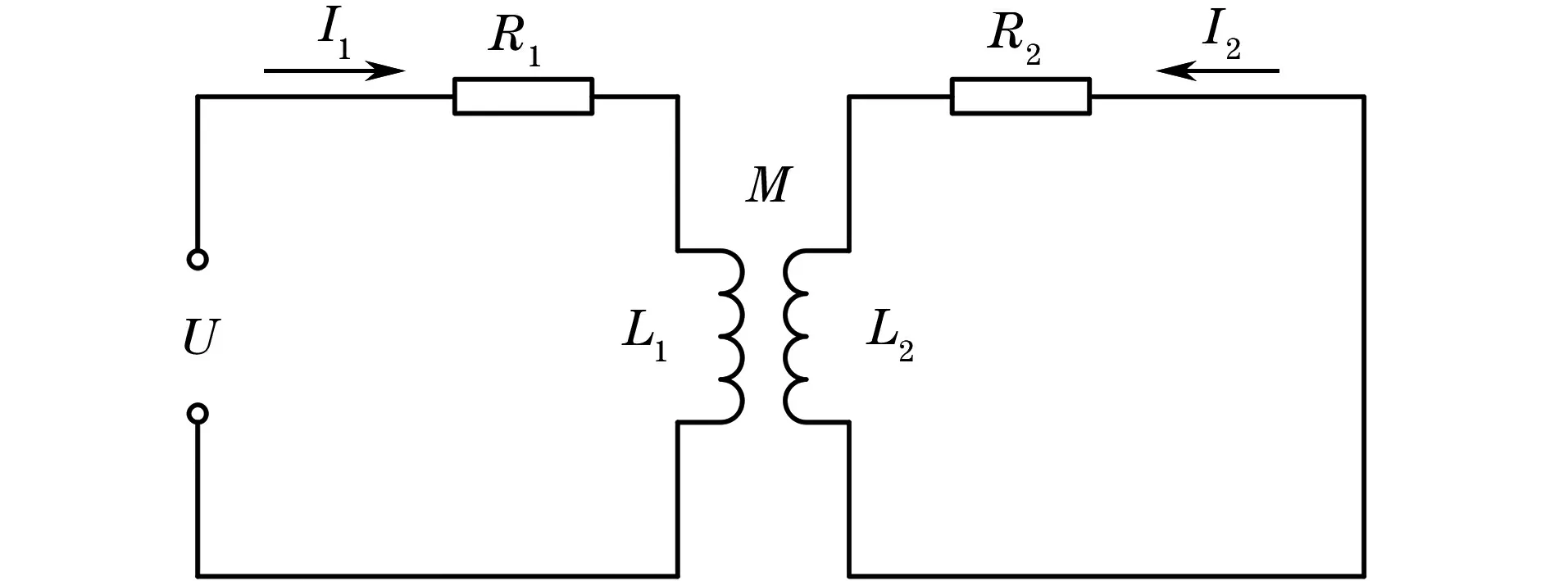
图5 单一激励频率下的脉冲涡流检测等效电路
求解式(1)可得

(3)
故等效电阻和等效电感可分别表示为

(4)

(5)
提离距离的变化会使互感系数M发生变化,由式(4)和(5)可知,M的变化会使等效电阻和等效电感发生变化,进而对脉冲涡流检测电压信号产生影响。
随着提离高度的增加,传播到试件表面的磁场强度逐渐减弱,试件所产生的涡流强度就会变小,使得检测信号电压幅值更小,同时信号幅值的衰减速率也会变快,直接影响到壁厚反演的精度,因此提离效应是影响带包覆层管道脉冲涡流检测结果的重要因素。为了进一步验证上述结论的正确性,利用 COMSOL软件开展仿真试验,得到有无提离条件下9 mm 厚试件所对应的感应电流密度(见图6),由图6可知,传感器提离后,试件中的感应电流密度明显减小,这就意味着渗透到试件中的涡流能量也变小。

图6 无提离及有提离条件下9 mm厚试件中的感应电流密度
以壁厚为9 mm的管道为例,在不同提离高度条件下对其进行检测,得到的原始感应电压信号如图7所示,再经单对数坐标转换得到的感应信号如图8所示。由图7,8可知,随着包覆层厚度的增加,检测电压幅值降低,信号衰减速度变快。之后,求解不同提离高度下检测电压信号所对应的晚期信号斜率,代入式(1)得到反演壁厚,然后计算壁厚反演误差(见表3)。由表3可知,利用无包覆层情况下建立的壁厚反演模型对带包覆层情况下的壁厚进行反演时,随着提离高度的增加,反演相对误差不断增大。
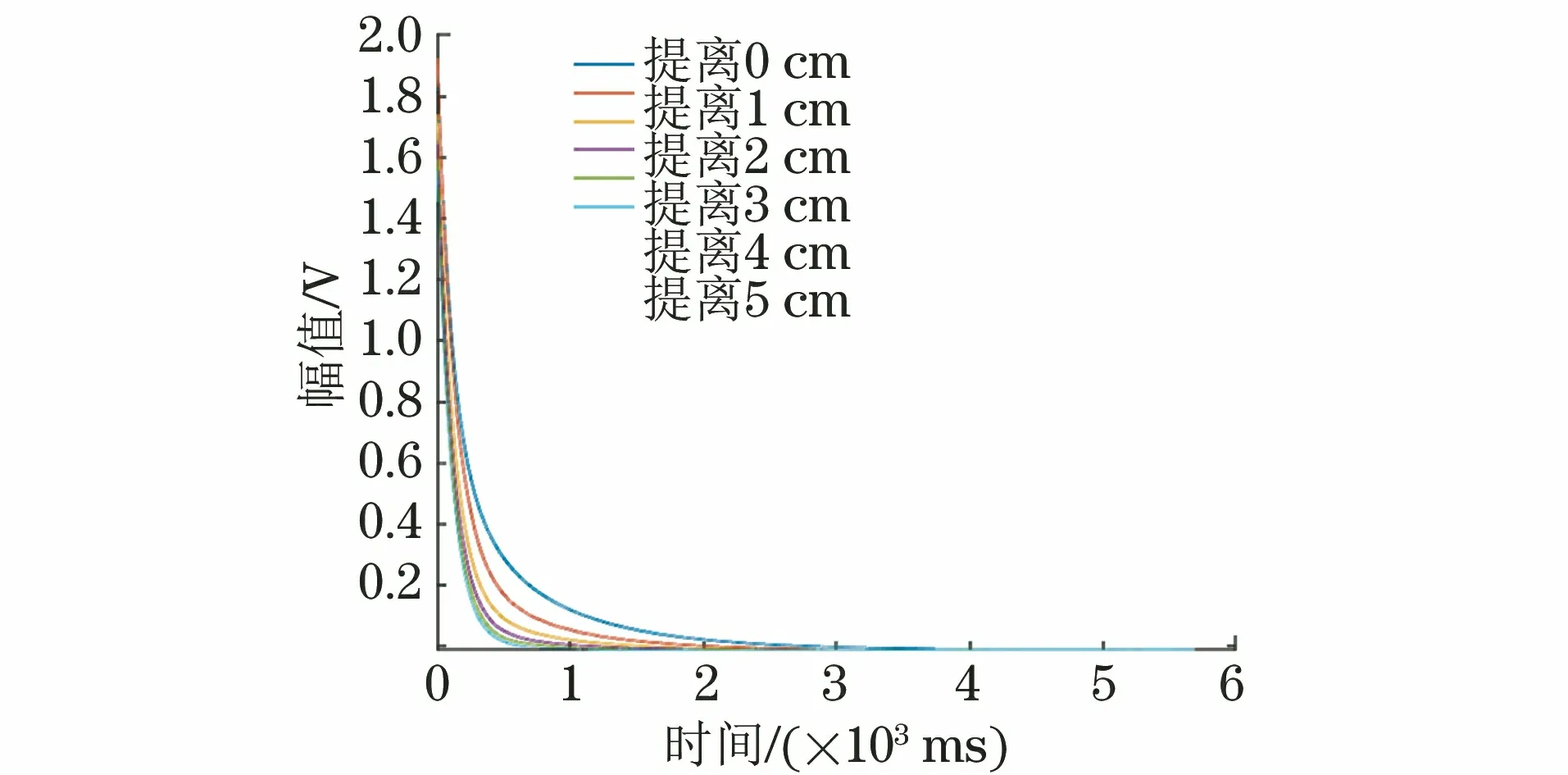
图7 不同提离高度下9 mm厚管道的检测信号
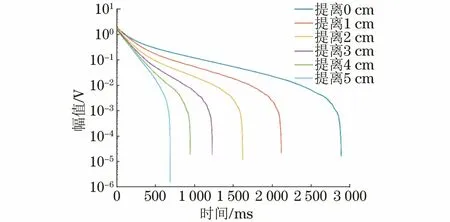
图8 单对数坐标系下不同提离高度时9 mm厚管道的检测信号
因此,壁厚反演模型需要根据提离高度的不同而改变。晚期信号斜率随提离高度的变化曲线如图9所示,由图9可知,提离高度与晚期信号斜率之间并不是简单的线性关系。

表3 不同提离高度下,9 mm厚管道的晚期信号斜率与反演壁厚关系

图9 9 mm厚管道的晚期信号斜率随提离高度的变化曲线
3 带包覆层的管道壁厚反演方法研究
由于无包覆层情况下建立的壁厚反演模型已不再适用于带包覆层的管道壁厚反演,为了保证检测结果的准确性,有必要开展带包覆层情况下管道的壁厚反演方法研究,以补偿提离效应带来的反演误差。
笔者提出了补偿提离效应的新思路,即将提离高度考虑在内,建立管道壁厚反演特征量和提离高度与壁厚之间的关系模型,模型以提离高度和壁厚反演特征量为输入,以壁厚为输出,即可实现带包覆层下的管道壁厚反演。
首先,将脉冲涡流探头提离高度逐步增大,测得不同提离高度下,不同厚度管道的晚期信号斜率。然后,使用MATLAB软件中的Curve Fitting Tool工具箱,以提离高度和晚期信号斜率为自变量,管道壁厚为因变量,拟合成三维曲面,并将该曲面模型参数编入数据采集处理软件中。在实际应用时,系统将采集到的感应电压的晚期信号斜率、测量包覆层厚度得到的提离高度输入该曲面模型中,就能计算出相应的管道壁厚。
3.1 带包覆层管道三维曲面壁厚反演模型的建立
在不同提离高度下,采用上述脉冲涡流检测系统对Q235钢管道进行壁厚测量。测量时,激励信号电压为20 V,频率为1.25 Hz,脉冲宽度为400 ms,占空比为50%,取脉冲方波的下降沿为感应电压信号的采集起始点。另外,由于目前采用的晚期信号斜率特征量只存在于检测信号的晚期,故对检测电压信号前端进行了削峰处理,同时将后期信号放大20倍。
在传感器提离分别为0,10,20,30,40,50 mm的情况下,对管道厚度分别为12,10.5,9,7.5,6,4.5 mm的区域进行测量,并提取各试件厚度的感应电压信号的晚期斜率。将晚期信号斜率作为x轴,提离高度作为y轴,管道壁厚作为z轴,建立空间直角坐标系,将测得的数据点依次放入坐标系中,如图10所示。图10反映了如下规律:当提离高度不变时,随着管道壁厚的增加,信号衰减速度变慢,晚期信号斜率变小;当管道壁厚不变时,随着提离高度的增加,信号衰减速度变快,晚期信号斜率变大。晚期信号斜率的物理含义是信号在试件中衰减的快慢,涡流信号在厚试件中的衰减速度要慢于在薄试件中的衰减速度,同时,由于随着提离高度的增加,信号在试件中的衰减速度会变快,所以在不同提离高度下,不同试件厚度的晚期信号斜率会呈现如图10所示的规律。利用MATLAB软件中的Curve Fitting Tool工具箱进行三维曲面拟合。拟合效果通常根据方程确定系数(R-Square)来确定,该值在01之间,越接近1说明拟合精度越高。当采用多项式拟合(Polynomial)时,方程确定系数(R-Square)最大,此时值为0.984 7,因此选用多项式拟合的方法来建立反演模型,拟合图如图11所示。

图10 晚期信号斜率-提离高度-壁厚的关系

图11 晚期信号斜率-提离高度-壁厚的三维拟合图
拟合得到的壁厚反演关系模型如式(6)所示,将测量得到的任一晚期信号斜率x和提离高度y代入该反演关系模型,都能计算出唯一确定的壁厚z。
z=f(x,y)=16.85-0.056 6x+1.941y+
0.000 086 22x2-0.001 412y+0.387 4y2-
0.000 000 511 3x3+0.000 009 049x2y-
0.000 034 42xy2
(6)
3.2 带包覆层管道三维曲面壁厚反演模型试验验证
建立三维曲面壁厚反演模型后,为了验证此模型的准确性以及反演误差,选取未加入到建模数据集中的数据作为验证数据,即在传感器提离分别为15,25,45 mm的情况下,对管道厚度分别为12,10.5,9,7.5,6,4.5 mm的区域进行测量,并分别求取各信号的晚期斜率。然后,将求解的晚期信号斜率与提离高度输入到反演模型中,即可得到壁厚反演测量值,再将其与真实值进行比较并计算反演误差,得到的晚期信号斜率与壁厚的关系如表4所示。
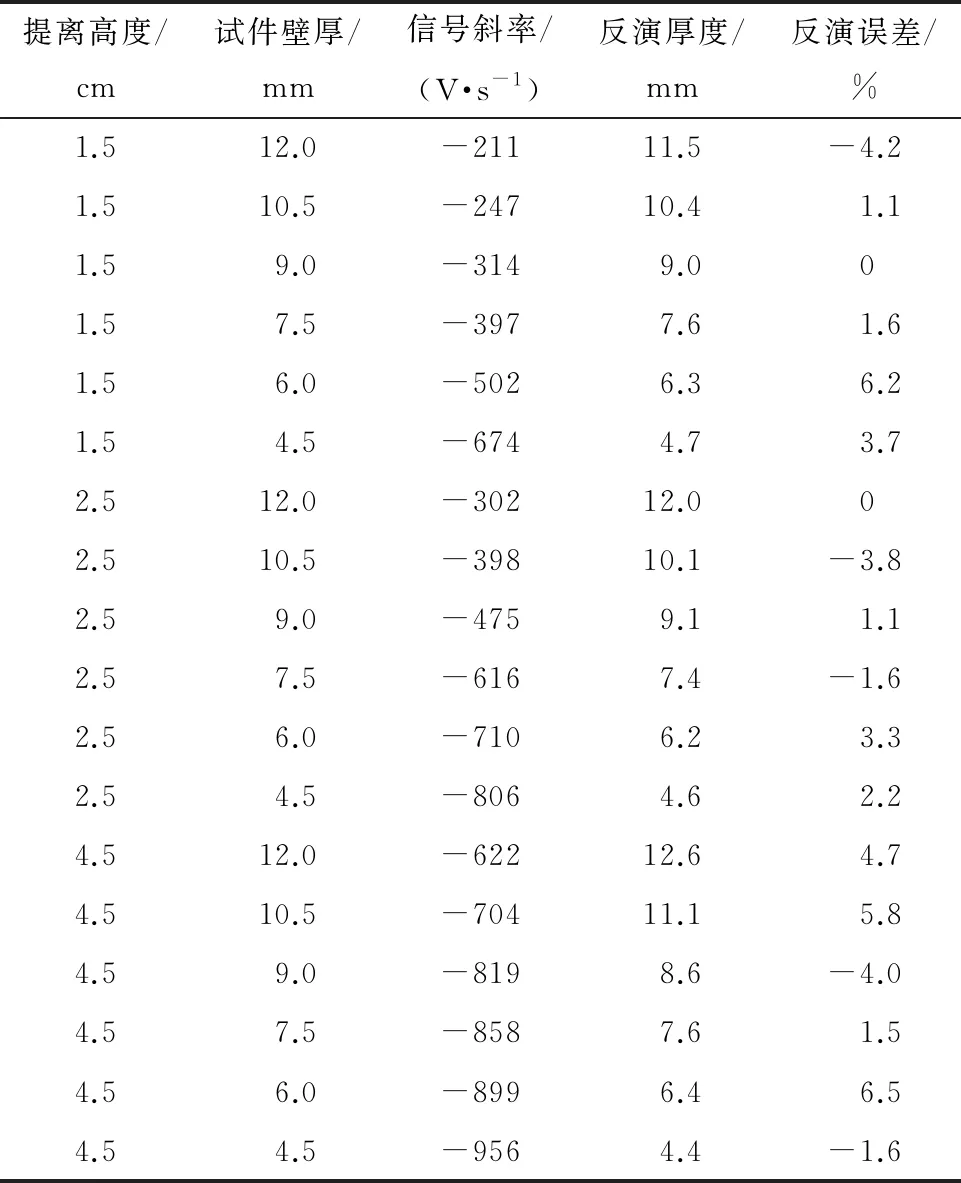
表4 不同提离高度下,晚期信号斜率与壁厚的关系(验证试验)
由表4可以看出,该壁厚反演模型的反演误差在7%之内,符合脉冲涡流检测标准以及现场检测指标。同时,证明了三维曲面壁厚反演关系模型在带包覆层壁厚检测中的可行性。
4 结语
对脉冲涡流感应电压信号进行分析,选取了晚期信号斜率作为壁厚反演的特征量,再通过分析晚期信号斜率、提离高度与管道壁厚的关系,得出晚期信号斜率会随提离高度的不同而变化,进而使反演误差增大的结论;并发现在不同提离高度下所得到的晚期信号斜率都与管道壁厚有着一一对应的关系,由此提出了一种基于三维曲面拟合的管道壁厚反演模型,并以Q235钢阶梯管道为被测试件,在不同提离高度下对各厚度区域进行了试验验证。结果表明,在较大提离(050 mm)条件下,该模型的反演误差能控制在 7%以内。同时,基于三维曲面拟合的管道壁厚反演模型也易于在上位机中实现,该模型对解决带包覆层管道壁厚的检测具有广泛的工程应用价值。

