基于激光超声纵波的钢轨内部缺陷检测方法

武 兴，缪建成，廖韦韬，郑 凯，王海龙

(1.江苏省特种设备安全监督检验研究院，南京 210036；2.海军装备部 装备项目管理中心，北京 100040；3.南京航空航天大学 自动化学院，南京 210016；4.江苏长城计算机系统有限公司，南通 226000)

导致钢轨失效的缺陷种类有很多，包括表面疲劳损伤、应力腐蚀、剥落等，以及位于钢轨亚表面或者内部的裂纹等。在大多数缺陷中，钢轨早期内部缺陷具有很大的危险性，且未发展成型，尺寸小，检测难度大，要求相应的检测技术必须具备很高的灵敏度。激光超声检测技术[1-3]作为一种新型的超声无损检测技术，是超声技术与光学技术的结合，该技术不仅结合了超声检测的优势，还能实现非接触、大面积快速扫描和高分辨率检测，而且激光器产生的脉冲宽度很窄，其最高频率可达几千兆赫兹，产生的波长只有几微米，对小缺陷敏感，在铁路内部小缺陷的无损检测中有较高的应用价值。

目前，在钢轨内部缺陷检测方面，GARCIA等[4-5]利用非接触式激光超声钢轨缺陷检测系统对钢轨表面和内部缺陷进行了检测；PANTANO等[6]建立了超声波在导轨和空气介质中传播的有限元模型，对钢轨轨头的内部缺陷进行了检测和分析，并通过试验验证了空气耦合探头用于导轨检测的有效性。虽然这些方法可以定性检测内部缺陷，但都未实现轨距角内部缺陷的检测。为了定量检测钢轨内部缺陷，笔者通过有限元仿真分析了超声纵波与内部缺陷的相互作用规律，利用波的衍射现象来研究纵波与内部缺陷之间的对应关系；通过建立缺陷定量检测计算模型，实现了不同长度钢轨内部缺陷的检测。

1 有限元数值模拟和理论分析

1.1 有限元建模和参数

基于激光激发超声波的热弹性机理，采用COMSOL有限元仿真软件建立了激光超声钢轨轨头轨距角内部缺陷检测模型。分析了超声纵波的传播时间、传播速度与缺陷大小的关系，进而定量计算轨距角内部缺陷的埋藏深度和长度。为了节省仿真时间，提高效率，选取长度为30 mm，厚度为20 mm的简化钢轨截面模型进行模拟，模型如图1(a)中虚线红框所示。有限元仿真中采用的A60钢轨材料特性参数如下：弹性模量为210 GPa;密度为7 840 kg·m-3;泊松比为0.29;热膨胀系数为1.18×10-5K-1。激光光源为点光源，半径为0.1 mm，脉冲上升时间为7 ns，激励点位置与内部缺陷端点的横向距离为8 mm，接收点从激励点开始向右15 mm，每个点间隔为0.1 mm[见图1(b)]。内部缺陷定义为槽型缺陷，缺陷的宽度H为0.01 mm，缺陷埋藏深度D为4 mm，长度L分别为0.50，0.75，1.00，1.25，1.50 mm。

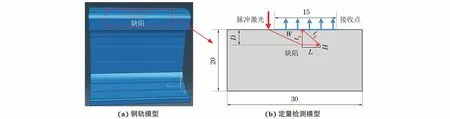
图1 脉冲激光辐照钢轨的有限元模型

1.2 钢轨的激光超声检测基础理论

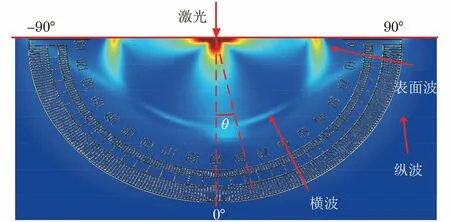
图2 各模态波声场指向示意

在激光热弹性机制中，当入射激光的能量密度低于材料的损伤阈值时，被测材料吸收激光能量转化为自身热能，在弹性范围内受热产生温度梯度而不足以熔化材料，其局部发生热膨胀并产生切向压力，在该机制激励下，钢轨材料内部产生表面波、掠面纵波、横波及纵波等模态的超声波。不同模态波的传播方向和速度都不同(见图2)，不同模态波的能量集中传播方向通过与钢轨表面法线的夹角θ表示，横波的能量集中方向为30°60°，纵波的能量集中方向为60°80°，主要在钢轨亚表面及内部传播；表面波的能量集中方向为90°。由此可了解到，当缺陷与激励点存在一定位移时，纵波对缺陷的灵敏度较高。

1.3 纵波定量检测的理论计算

脉冲激光在钢轨上可同时激发多种模态的超声波，根据惠更斯原理，纵波在钢轨内部传播时，存在两条传播路径，一是经过缺陷左端点发生衍射后到达接收点，二是沿缺陷表面传播一段时间后，在缺陷右端点发生衍射后到达接收点。假设纵波波速为vL，则根据波速、纵波到达接收点的飞行时间以及激励与接收距离W的关系，t1和t2可表示为

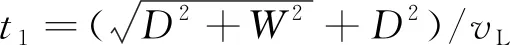
(1)

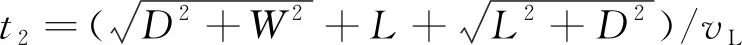
(2)

根据式 (1)，缺陷的埋藏深度D可表示为

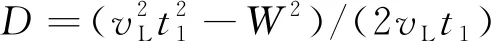
(3)

当W与t1已知时，内部缺陷的埋藏深度可通过式(3)计算得到，缺陷长度可表示为

L≈(t2-t1)vL

(4)

2 仿真结果与分析

图3为不同时刻激光超声衍射纵波位移云图。激光辐照到材料表面时会激发多种模式的声波，如瑞利波(R波)、掠面纵波(P波)、纵波(L波)和横波(S波)。当L波遇到内部缺陷时，一部分L波在缺陷始端发生衍射，转换为衍射波(LL1)，如图3(b),3(c)所示；另一部分L波会继续沿着缺陷上表面传播到缺陷末端，形成衍射波(LL2)，如图3(d),3(e)所示。

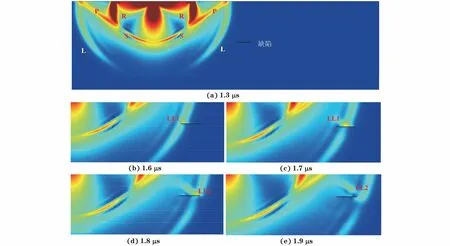
图3 不同时刻的激光超声衍射纵波位移云图

LL1的传播时间变化主要取决于缺陷的埋藏深度，而LL1与LL2的到达时间差则取决于缺陷的长度变化。为了验证衍射纵波与缺陷长度之间的对应关系，建立了不同长度内部缺陷的仿真模型。缺陷长度L分别为0.50，0.75，1.00，1.25，1.50 mm。

图4为钢轨内部无缺陷与不同长度内部缺陷的激光超声B扫描位移图像。当钢轨内部没有缺陷时，B扫描图像以表面波和掠面纵波为主；当钢轨内部存在缺陷时，激光激发的L波与内部缺陷发生衍射转化为LL波，如图4(b)所示。当缺陷的长度从0.5 mm增加到1.5 mm时，LL波的宽度也逐渐增加，如图4(c)4(f)中红圈部分所示，这是因为缺陷的长度增加了，而缺陷左端产生的LL1波到达接收点的时间相同，在缺陷右端产生的LL2波到达接收点的时间会随着缺陷长度的增加而增加。

为了验证上述思路是否可以用于定量检测内部缺陷，需要进一步分析LL波的时域信号。图5为接收点距离激励点8 mm处激光产生的超声波与不同长度内部缺陷相互作用的归一化位移曲线。由图5可知，随着缺陷长度的增加，LL1波的到达时间几乎没有改变，而LL2波的到达时间会随着缺陷长度的增加而增加，其规律与上述B扫描位移图像显示的一致。进一步说明可以用这种方法来定量检测内部缺陷的长度。

通过时域信息中LL1与LL2到达的时间，结合公式(3)与(4),即可定量计算缺陷的埋藏深度和长度。图6为内部缺陷D=4.0 mm，L=0.5 mm，H=0.01 mm时接收点距离激励点8 mm处激光超声的归一化位移曲线。由图6可知，P波、LL波和R波的到达时间分别为1.428，2.258，2.696 μs。计算得到的P波速度(5 602 m·s-1)与理论值[7](5 924 m·s-1)基本一致，同时计算得到的R波速度(2 967 m·s-1)与理论值[8](2 977 m·s-1)一致。将LL1波的到达时间(2.258 μs)代入到式(3)中，假设LL波波速(与P波相同)为5 924 m·s-1，计算得到缺陷的埋藏深度为4.29 mm，与实际深度基本一致；将LL2波的到达时间代入到式(4)中，计算得到缺陷的长度为0.52 mm，与实际长度基本一致。因此，激光超声纵波可以有效地对钢轨内部缺陷进行定量检测。

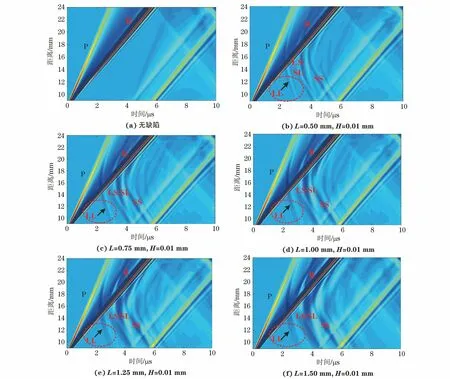
图4 钢轨内部无缺陷与不同长度内部缺陷的激光超声B扫描位移图像

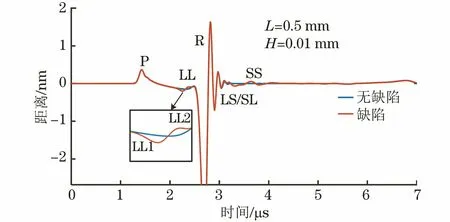
图6 激励-接收间距为8 mm时的激光超声归一化位移曲线

表1 不同长度内部缺陷时LL1波和LL2波到达接收点的时间

表1为不同长度内部缺陷时LL1波和LL2波到达接收点的时间，由表1可知，t1，t2的相对误差均在4%之内，所以使用该检测方法可以准确地定量检测内部缺陷的大小。

3 结语

研究了激光超声与钢轨不同长度内部缺陷之间的相互作用规律，并提出一种有效的检测钢轨内部缺陷的方法，建立了有限元仿真模型和定量计算模型，通过超声纵波衍射规律来量化内部缺陷的大小。当缺陷与激励点存在一定相对位移时，缺陷对L波的影响比较明显。L波与缺陷产生衍射现象，从而转换成LL波，LL波的宽度也会随着缺陷长度的增大而增大,即LL1波到达接收点的时间不变，LL2波到达接收点的时间增加，以此来定量计算内部缺陷的大小。后期将建立激光超声试验系统来验证此方法的有效性。