强化审题意识深化知识理解拓展思维深度完善认知结构——以解析几何高考复习题为例

安徽省合肥市第四中学(230000) 郑 良

江苏省睢宁县新城区实验学校(221200) 苗 勇

一、问题提出

众所周知, 多数学生认为解析几何试题思路清晰可见,目标却遥不可及.究其原因是学生只注意到问题的常规与表象,没有挖掘到题目的隐含信息,不能将关键信息合理转化,不能因地制宜地采用不同策略与恰当的方式进行表征,无法在条件与结论之间架起易于通达的桥梁.长此以往,解析几何是学生“心中永远的痛”,导致其未战先怯、敬而远之.教学中,教师要强化学生的审题意识(审题是解题的第一步,关乎解题的成败,学生要在仔细审题与快速做题中找到平衡点),提高学生审题能力.通过细化审题,通观全局、聚焦局部、整体思维,在宏观与微观中转换,在不同方案中思辨,合理部署解题路径与谋划可能的调整预案,切实避免各种不必要的繁琐运算.数学审题审什么? 怎么审? 罗增儒教授在文[1-2]中分别结合案例给出了审题的认识、考试中的审题操作.余锦银老师在文[3]中给出了数学审题策略的5 个方面,请有兴趣的读者参阅.本文以几道解析几何试题为载体,力争展示研习试题结构特征、条件转译方法、分析调整解题方略的过程,以期能对读者分析、调整、化繁为简、逐步优化的解题有所帮助.不足之处,敬请同仁批评指正.

二、典例试题剖析

1 强化整体布局,选取合适变量

凡事预则立,不预则废.解析几何试题经常会出现动点或动直线,点和直线之间互相制约,互相依存.引入参变量,使诸多相关或不相关的量统一到这个参变量之下,达到减少未知数的个数、简化题目条件、减少计算量的目的.但参变量的选择多种多样,既可以选择点的坐标为参变量建立目标函数,也可以直线的斜率为参变量建立目标函数,解题时要兼顾计算简便的需要,要对计算量有一定的预判,选择合适的参变量.

例1已知O为坐标原点,直线l与椭圆交于A,B两点,且OA⊥OB,求ΔAOB的面积S的取值范围.

解由OA⊥OB,可设A(x0,y0),B(λy0,−λx0)(由对称性可取λ ＞0,其几何意义是λ=当B点分别位于短轴和长轴端点时,λ取得最小值和最大值),则

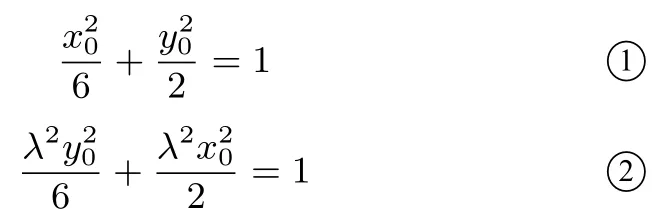
在②两边同除以λ2后与①相加,得故由对勾函数f(λ) =λ+(λ ＞0)的单调性可知,f(λ)mⅰn=f(1) = 2,f(λ)max=所以ΔAOB的面积S的取值范围是

点评本题中出现直线OA与OB垂直,一般设其斜率分别为k,(当其中一条直线斜率为0,另一条直线斜率不存在时,单独计算),将求解目标S表示为k的函数;也可设直线l的方程为y=kx+m(斜率不存在时,单独计算),利用一元二次方程根与系数的关系及条件中的垂直关系,建立面积S的表达式.以上解答从两向量垂直的角度,设A,B两点坐标分别为(x0,y0),(λy0,−λx0),分别代入椭圆方程,整体代换,优化了计算过程.在处理直线夹角与线段距离时,若能根据条件合理选择向量工具,往往能事半功倍.使用的前提是深入理解题意,联系相关知识,洞悉问题本质.

2 优化图形结构,关注几何性质

解析几何是数形结合的典范,解决解析几何问题应有几何视角与代数视角.几何视角即从几何的角度处理解析几何问题,代数视角即从代数的角度处理解析几何问题.彼此交融,相得益彰.令人遗憾的是,不少师生对解析几何理解出现偏差,出现思维定式甚至将解析几何异化为计算科学.解析几何最重要的特点是用代数方法来处理几何问题,然后将代数运算的结果映射到几何图形.但平面解析几何的源泉是几何,图形是直观表现形式,是问题的起点和归宿.处理相关问题时应首选几何视角, 挖出题中所蕴含的轨迹或几何性质,从而简化运算.代数方法仅仅是工具,是几何视角的有力补充,如不同几何图形的代数表示可能是统一的.因此,在处理解析几何问题时要重视代数运算,但也绝不能忽视研究对象的几何属性,若能聚焦图形的几何性质,恰当转译,可能会使运算简便.

例2如图1,圆O与离心率为的椭圆1(a ＞b ＞0)相切于点M(0,1).

(1)求椭圆T与圆O的方程;

(2) 过点M引两条互相垂直的直线l1,l2与两曲线分别交于点A,C与点B,D(均不重合).若P为椭圆上任一点,记点P到两直线的距离分别为d1,d2,求的最大值.

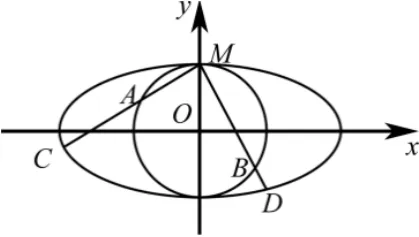
图1

解(1)椭圆T的方程为圆O的方程为x2+y2=1.(过程略)

(2)设过点P(异于C,D,M)分别与l1,l2垂直的直线与l1,l2分别相交于E,F两点,则四边形MEPF为矩形,所以=PM2(当P与C,D,M重合时也成立),设P(x,y),则=PM2=x2+(y −1)2=4−4y2+(y −1)2=当且仅当y=时等号成立.故当取得最大值为

点评本题自然的想法是设直线l1,l2的斜率为运用点到直线的距离公式,将d21+d22表示为变量k的函数,再求其最大值.若注意到四边形MEPF为矩形,以静制动,将(两个量均在变化)转化为PM2(点M为定点),目标函数的建立更直接,其最大值的求解更简单.点、线、三角形、圆等是平面几何的基本研究对象,它们拥有很好的性质,如角平分线定理、线段的垂直平分线定理、相似三角形的性质、三角形的中位线定理,圆的垂径定理,直径所对的圆周角为直角,同弧所对的圆周角相等等.处理平面解析几何问题时,要善于根据图形的特征联想到相关性质,直接利用性质(结论)对问题化繁为简,甚至开辟一片新天地.

例3已知椭圆= 1 的左、右焦点分别为F1、F2, 连结椭圆上不同两点A,B满足AB//x轴, 过点A作AF2的垂线l1,过点B作BF2的垂线l2,且l1,l2的交点为C.

(1)求ΔABF2面积的最大值;

(2)求证: 过点A,B,C的圆D在x轴上截得的弦长为定值.

(1)解ΔABF2面积的最大值为√(过程略)

(2)证明由题意知∠F2AC= ∠F2BC= 90°, 故点A,F2,B,C共圆于以CF2为直径的圆D,又A,B两点关于y轴对称,所以y轴是圆D的对称轴,所以F2关于y轴对称的点F1也在圆D上,故过点A,B,C的圆D在x轴上截得的弦为定弦F1F2,其长为定值2.

点评本题第(1)小题可用均值不等式或椭圆的参数方程求ΔABF2面积的最大值;第(2)小题若以点A的横坐标作为变量表示圆D的方程,再计算圆D在x轴上的截距,计算过程繁琐,根据四点共圆的判定可知A,B,C,F2共圆于圆D,结合椭圆的对称性可知所求的弦为F1F2.教学时要引导学生“多一点想,少一点算”,通过解题反思培养学生追根溯源的习惯.通过知识的积累,解题经验的丰富,提高审题能力,力争解题时少走弯路.

3 关注元素地位,巧用“对等”关系

几何图形中的点与点、线与线等对象互换位置,并不影响问题的条件和结论,我们将几何对象具有的这种关系称为“对等”关系.具有“对等”关系的计算过程往往是重复的、可“复制”的,因此只需计算一次,替换即可得到另一个计算结果,减少了计算量.解题中要注意挖掘“对等”关系,优化解题过程.

例4已知点A为椭圆= 1 的左顶点,点F为椭圆C的右焦点.P为椭圆C上位于x轴上方的点,直线PA交y轴于点M,过点F作MF的垂线,交y轴于点N,直线AN交椭圆C于另一点Q,求ΔAPQ的面积的最大值.

解设AP,AQ的斜率分别为k1,k2, 则直线AP的方程为y=k1(x+4), 令x= 0, 得M(0,4k1), 同理可得N(0,4k2), 由MF⊥NF, 得k1k2=将y=k1(x+4)代入= 1, 得得xP=将点P坐标中的k1换成k2(即),可得xQ=所以P,Q两点关于原点对称,所以SΔAPQ= 2SΔAOP=AO·|yP|≤ab=即ΔAPQ的面积的最大值为

点评命题者提供的解题思路是设直线AP的方程,依次求出M,P的坐标, 利用垂直关系求出N的坐标, 再求AN的方程,AN的方程与椭圆C的方程联立,求出点Q的坐标,最后得P,Q两点关于原点对称.解题思路完全被题目中点、线的生成的逻辑顺序“牵”着走,逻辑清楚,思路自然,计算量大.如果注意到P,Q的“对等”地位,分别从P,Q出发作相同的运算,就会有类同的结果,重复的工作只做一次,使解题过程得到简化.教学时,可尝试通过相关试题的比对,让学生明晰问题的逻辑关系,逐步提高与完善学生的推理论证能力,培养学生的理性精神,这也是数学教学的目的.

4 特殊寻求目标,一般跟进证实

解析几何中常会遇到定值(定点、定数值、定曲线等)问题, 由于涉及较多字母, 导致运算过程较为复杂, 难以为继,如果先根据图形所处的特殊位置,猜出结果,这样就使解题有了明确的目标和方向,将部分字母的运算转化为数的运算,可以简化解题过程.

例5过点的动直线l与椭圆交于A,B两点, 试问坐标平面上是否存在定点N, 使得以AB为直径的圆恒过点N? 若存在,求出点N的坐标;若不存在,请说明理由.

解当l分别垂直于两坐标轴时, 易知圆的方程为x2+y2= 1 和两圆方程联立可求得其公共点为(0,1).下面只需考察当直线l斜率存在且不为0 时, 以AB为直径的圆是否过点N(0,1).设l的方程为y=代入椭圆C方程整理得(9+18k2)x2−12kx −16 = 0.设A(x1,y1),B(x2,y2), 则x1+x2=x1x2+(y1−1)(y2−1)=···=0(过程略),所以

综上所述,坐标平面上存在定点N(0,1),以AB为直径的圆恒过N(0,1).

点评解答先从直线l的两种(可能需要更多种)特殊的位置出发,得到两圆的公共点N(0,1),实现了化无限为有限,化抽象为具体的过程.动圆过N(0,1)是动圆过定点的必要条件,然后再验证其充分性,使解题有了方向和目标,起到了化繁为简,减少运算的功效.

5 尝试联想推理,实现无中生有

审题时不仅要全面梳理题目的显性条件,还要挖掘题目的隐性条件.若能根据题设与结论不断联想与推理,创设相关条件优化解答,不但解法给人耳目一新的感觉,更能促进学生对相关知识的理解,实现创新思维的提升.

例6已知椭圆C1:设点P为椭圆= 1 上一点, 过点P作椭圆C1的两条切线l1,l2,斜率分别为k1,k2,求证:k1·k2为定值.

证明设过P(x0,y0)与椭圆C1相切的直线l的斜率为k,故其方程为y −y0=k(x −x0),代入椭圆C1的方程消去y,得(4k2+1)x2+8k(y0−kx0)x+4[(y0−kx0)2−1]=0.因为直线l与椭圆C1相切,所以关于x的一元二次方程的判别式为0,整理得(4)k2−2x0y0k+y02−1 = 0,当4=0 时,直线l的斜率为0 或不存在.所以k1,k2为关于k的一元二次方程(4)k2−2x0y0k+y02−1=0 的两根,从而k1·k2=又点P(x0,y0)在椭圆C2上,所以所以k1·k2=为定值.

点评本题为“圆锥曲线中的双切线”问题,解答将k1,k2抽象为k,利用直线与椭圆相切的关系,根据求解目标以k为主元整理出关于k的一元二次方程,利用两切线的斜率是此方程的两个根,从而使用韦达定理解决问题.将k1,k2抽象为k、以k为主元为解题目标的需要,也是学生数学抽象素养的体现.联想是以旧促新,通过相对熟悉的情境回扣相关的知识、方法、思想,从而尝试全方位的比对与迁移.无中生有则要明晰问题差异,揭示问题本质,体现出思维的创造性,实现内容理解的融会贯通,它是学生高阶思维的重要标识.教师要改变观念,用新的眼光去审视熟悉的问题,从不同角度去深入研究,深化对相关内容的理解.教学时教师要大胆放手,必要时给予引导,使学生拾阶而上,从肤浅到深入、从现象到本质、从常规到创新,相信学生会给出很多“看似意料之外、实乃情理之中”的方案,让创新成为学生的不懈追求.

三、结束语

苏步青先生说过:“学习数学要多做习题,边做边思索,先知其然,然后知其所以然.”教师在平时的教学中,在重视学生基础知识的夯实、通性通法的掌握、数学思想的领悟、基本策略的转换的基础上,还要培养学生从数学角度发现问题与提出问题、分析问题与解决问题的能力,通过(理论与实践)案例培养学生的整体观念与创新意识,让思维转换在学生学习生活中散发光芒.