三角公式的图形表示

新疆乌鲁木齐市新疆师范大学数学科学学院(830017) 胡明茹 杨 军

三角公式因内容繁多、结构复杂,导致其记忆难度较大,容易混淆,进而难以理解公式本身的意义.数学公式反映了数学对象的属性之间的关系,具有一定的形式符号化的抽象性和概括性的特征[1].若借助图形直观表征三角公式,则有助于理解公式的内在涵义.正所谓“数缺形时少直观,形缺数时难入微; 数形结合百般好,隔离分家万事休”(华罗庚教授语).本文利用单位圆中的三角函数线,对平方关系、半角的正切公式、两角差与和的余弦公式、正弦公式、正切公式进行直观的表征,以实现数学公式可视化的目的.

一、平方关系

如图1 所示的单位圆中, 角α的顶点在原点, 始边与x轴非负半轴重合, 终边与单位圆交于点P.分别作出角α的正弦线MP、余弦线OM、正切线AT、余切线BS、正割线OT、余割线OS.则易知OM2+MP2= 1,即sⅰn2α+cos2α=1;AT2+OA2=OT2,即tan2α+1=sec2α;BS2+OB2=OS2,即cot2α+1=csc2α.

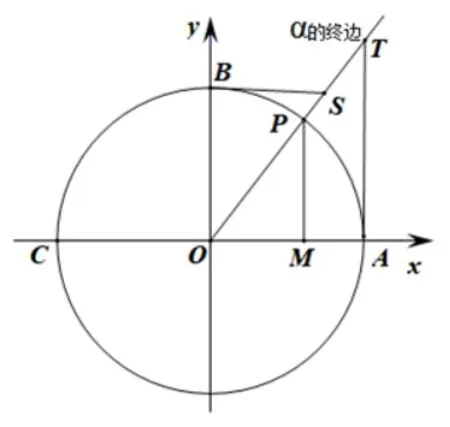
图1

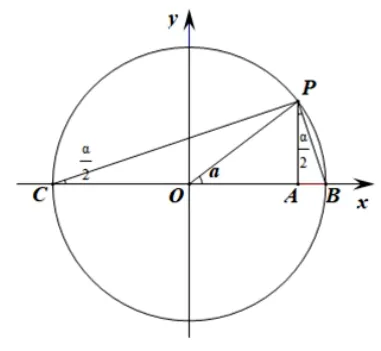
图2

二、半角的正切公式

实现半角正切公式的图形表示的关键是构造出半角.为此先构造锐角的半角,进而推广到任意角的情形.

如图2 所示的单位圆中,角α以x轴非负半轴为始边且与单位圆交于点B,其终边与单位圆交于点P.设单位圆与x轴负半轴交于点C, 连接PC,PB, 由同弧或等弧所对的圆周角等于圆心角的一半,知∠PCB=过点P作PA垂直于x轴, 垂足为A, 那么AP为角α的正弦线,OA为角α的余弦线.利用锐角正切的定义以及三角函数线可知

注意到直径所对的圆周角∠CPB= 90°,而∠PAB=90°, 从而∠PBA在两个不同的直角三角形中的余角相等, 即∠APB= ∠PCA=同理可知角α为任意角时,同理利用正切的定义以及三角函数线也可以表示角的正切值.不妨设α为第一象限角且终边与单位圆交于点P,那么角的终边落在第一或第三象限,且与单位圆分别交于点Q、点R(图3).注意到正切函数最小周期为π,所以只需考虑角的终边落在第一象限的情形即可.

分别作角α和的正弦线AP,BQ,显然

设单位圆与x轴负半轴交于点C,连接PC,由同弧或等弧所对的圆周角等于圆心角的一半,知∠QOB= ∠PCB.根据平行的判定定理易知OQ//CP,所以ΔPCA∽ΔQOB,从而

这样,就得到了半角正切公式的图形表示,从而使得难以记忆的半角正切公式有了直观鲜活的意义.

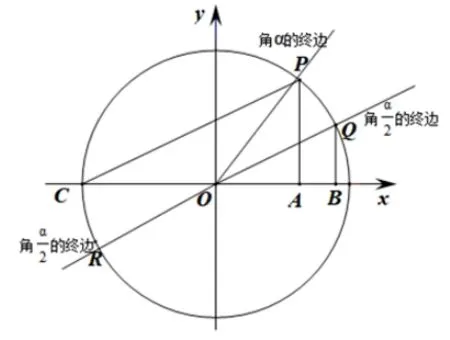
图3

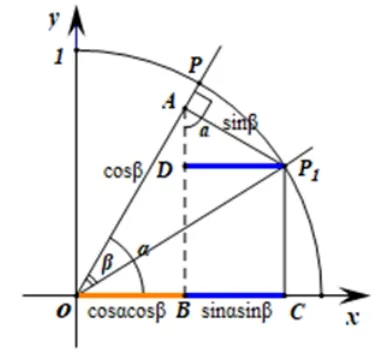
图4

三、两角差与和的余弦、正弦公式

教科书是通过向量数量积推导两角差的余弦公式,进而运用诱导公式得到其他三角公式的.这种方法看起来相对简单,但却显得比较突兀、不自然.借助三角函数线推导两角差的余弦公式,虽然推导过程略显复杂,但思路比较自然,并且比较契合学生的认知水平.

注意到任意角的情形均可以通过诱导公式化归为锐角,所以下面关于两角和差的三角公式的图形表示均以锐角为例.

(一)两角差的余弦、正弦公式

设角α,β为锐角,且β ＜α.如图4 所示的单位圆中,角α以x轴非负半轴为始边,其终边与单位圆交于点P.构造∠POP1=β且β的另一边与单位圆交于点P1.则角α −β是以x轴非负半轴为始边,以OP1为终边的角.

过点P1作P1C垂直于x轴,垂足为C,那么OC为角α −β的余弦线,即cos(α −β)=OC;CP1为角α −β的正弦线,即sⅰn(α −β)=CP1.因此,只需用角α,β的正弦线和余弦线表示OC,CP1即可.

过点P1作P1A垂直于OP,垂足为A.则在RtΔAOP1中, 有OA= cosβ,AP1= sⅰnβ.过点A作AB垂直于x轴,垂足为B.则在RtΔOBA中,有OB= cosαcosβ.过点P1作P1D垂直于AB,垂足为D.注意到∠P1AD=α,故在RtΔAP1D中,有DP1= sⅰnαsⅰnβ.又BC=DP1,于是OC=OB+BC=OB+DP1=cosαcosβ+sⅰnαsⅰnβ,即得到两角差的余弦公式cos(α−β)=cosαcosβ+sⅰnαsⅰnβ.

如图5 所示, 在RtΔOBA中, 有BA= sⅰnαcosβ.在RtΔAP1D中, 有DA= cosαsⅰnβ.又CP1=BD, 于是CP1=BD=BA −DA= sⅰnαcosβ −cosαsⅰnβ,即得到两角差的正弦公式sⅰn(α −β)=sⅰnαcosβ −cosαsⅰnβ.

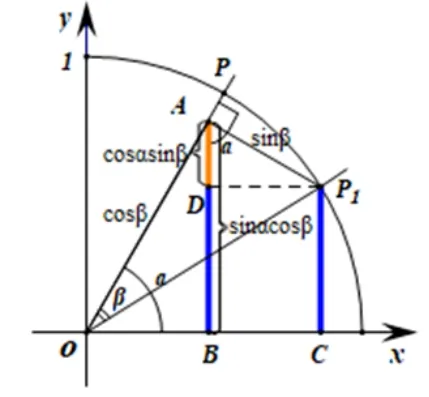
图5

图6

(二)两角和的余弦、正弦公式

设角α,β为锐角, 如图6 所示的单位圆中, 角α以x轴非负半轴为始边, 其终边与单位圆交于点P1.构造∠P1OP=β且β的另一边与单位圆交于点P.则角α+β是以x轴非负半轴为始边,以OP为终边的角.

过点P作PC垂直于x轴, 垂足为C, 那么OC为角α+β的余弦线,即cos(α+β) =OC;CP为角α+β的正弦线,即sⅰn(α+β) =CP.因此,只需要用角α,β的正弦线和余弦线表示OC,CP即可.

过点P作PA垂直于OP1, 垂足为A.则在RtΔPOA中, 有PA= sⅰnβ,OA= cosβ.过点A作AB垂直于x轴, 垂足为B.则在RtΔOBA中, 有OB= cosαcosβ.过点A作AD垂直于CP,垂足为D.注意到∠APD=α,故在RtΔAPD中, 有DA= sⅰnαsⅰnβ.又CB=DA, 于是OC=OB −CB=OB −DA=cosαcosβ −sⅰnαsⅰnβ,即得到两角和的余弦公式cos(α+β)=cosαcosβ−sⅰnαsⅰnβ.

如图7 所示, 在RtΔOBA中, 有BA= sⅰnαcosβ.在RtΔAPD中, 有DP= cosαsⅰnβ.又CD=BA, 于是CP=CD+DP=BA+DP=sⅰnαcosβ+cosαsⅰnβ,即得到两角和的正弦公式sⅰn(α+β)=sⅰnαcosβ+cosαsⅰnβ.

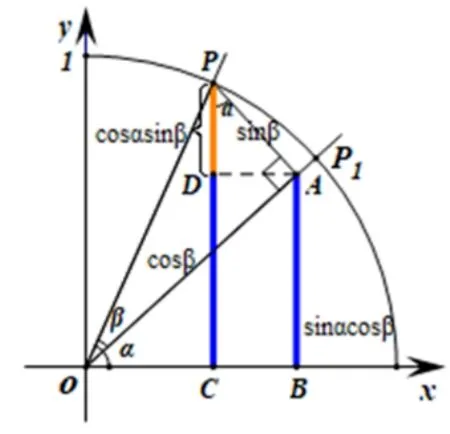
图7

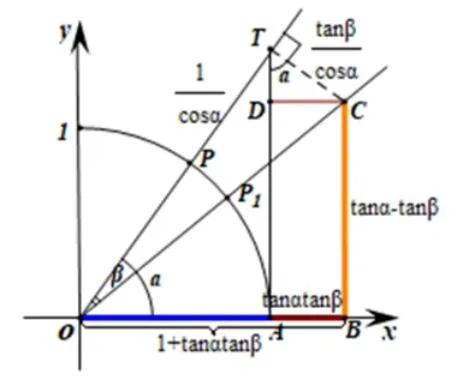
图8

四、两角差与和的正切公式

(一)两角差的正切公式

设角α,β为锐角,且β ＜α.如图8 所示的单位圆中,角α以x轴非负半轴为始边且与单位圆交于点A,其终边与单位圆交于点P.构造∠POP1=β且β的另一边与单位圆交于点P1.则角α −β是以x轴非负半轴为始边,以OP1为终边的角.

过点A作单位圆的切线交角α的终边于点T, 则AT= tanα, 进而OT=过点T引TC垂直于OT, 且与角β的终边OP1交于点C.则在RtΔOCT中,由tanβ=知CT=过点C作CB垂直于x轴,垂足为B,则tan(α −β)=因此,只需要利用α,β的正切线表示即可.

过点C作CD垂直于AT, 垂足为D, 则AB=DC,BC=AD.注意到∠CTD=α, 故在RtΔCTD中,由sⅰnα=知DC= tanαtanβ; 由cosα=知DT=tanβ.在RtΔOBC中,根据正切的定义及三角函数线可知tan(α −β) =即tan(α −β)=

(二)两角和的正切公式

设角α,β为锐角, 如图9 所示的单位圆中,角α以x轴非负半轴为始边且与单位圆交于点B,其终边与单位圆交于点P1.构造∠P1OP=β且β的另一边与单位圆交于点P.则角α+β是以x轴非负半轴为始边,以OP为终边的角.

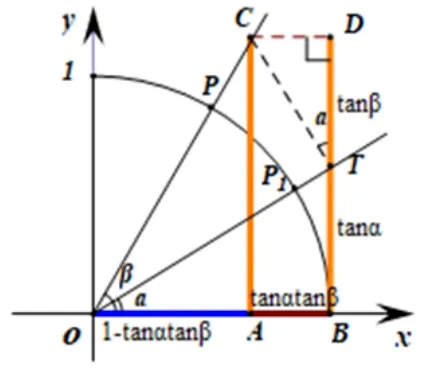
图9

过点B作单位圆的切线交角α的终边于点T, 则BT= tanα, 进 而OT=过点T引TC垂直于OT,且与角β的终边OP交于点C.则在RtΔOTC中,由tanβ=知TC=过点C作CA垂直于x轴,垂足为A,则tan(α+β)=因此,只需要利用α,β的正切线表示即可.

过点C作CD垂直于BT,并交BT的延长线于点D,则AB=CD,AC=BD.注意到∠CTD=α,故在RtΔTDC中,由sⅰnα=知CD= tanαtanβ;由cosα=知TD= tanβ.在RtΔOAC中,根据正切的定义及三角函数线可知tan(α+β) =即tan(α+β)=

本文通过三角函数线推导三角公式,从而实现复杂、抽象的三角公式可视化.这种直观呈现的方式,能够激发学生的学习兴趣、培养学生的创造性思维,使得数学知识的学习变得简单、自然、易于理解.