一题五探
山西省太原市第三实验中学(030031) 董立伟
普通高中课程标准实验教科书《数学4·必修·A 版》(人民教育出版社,2007年2月第2 版)第147 页复习参考题B组第7 题如下:
题目如图1,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点.当ΔAPQ的周长为2 时,求∠PCQ的大小.
与教科书配套的《教师教学用书》第131 页给出了本题的如下基于三角恒等变换视角的解答:
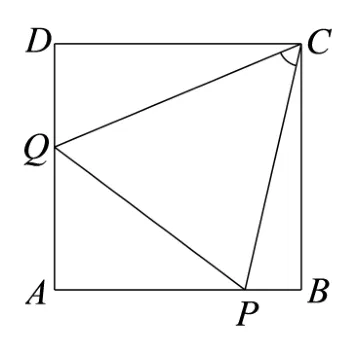
图1
设AP=x,AQ=y, ∠BCP=α, ∠DCQ=β, 则tanα=1−x,tanβ=1−y.于是
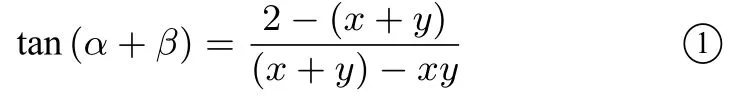
又ΔAPQ的周长为2,即x+y+变形可得
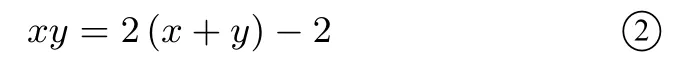
于是tan(α+β) =又0<α+β <所以α+β=
本文沿用上述解答中各几何量的表示法,在此基础上对本题做深入探究.
探究一本题还有其他的解题视角吗?
解法一(平面向量的视角)建立如图 2 所示平面直角坐标系.则P(x,0),Q(0,y),C(1,1).所 以,(x −1,−1),= (−1,y −1).cos ∠PCQ=
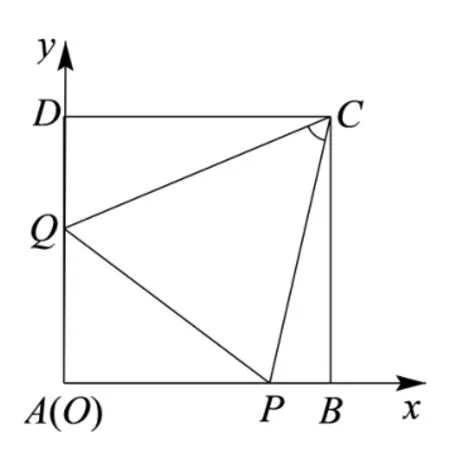
图2
展开即
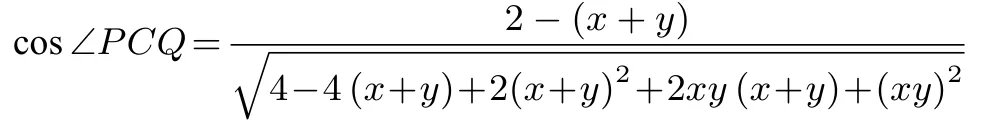
将②代入上式并化简得到
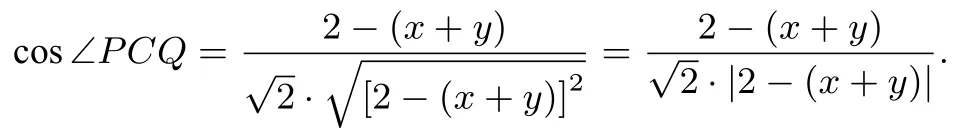
因为0< x,y <1, 所以, cos ∠PCQ=又因为0<∠PCQ <所以,∠PCQ=
解法二(解三角形的视角)AP=x,AQ=y, 所以PB= 1−x,QD= 1−y,PC== 2−(x+y).在ΔCPQ中,由余弦定理有
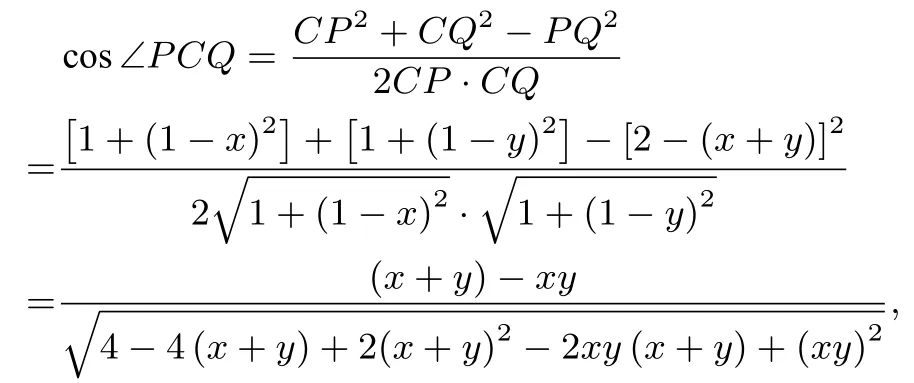
将②代入上式并化简得
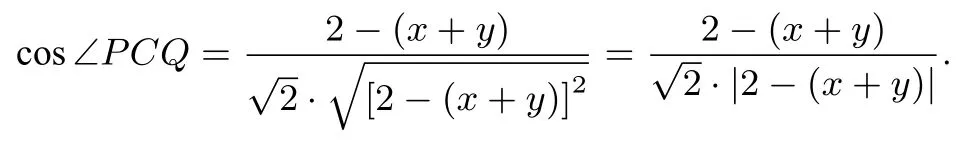
因为0< x,y <1, 所以, cos ∠PCQ=又因为0<∠PCQ <所以,∠PCQ=
解法三(平面几何的视角)如图3, 延长AB至点S, 使BS=DQ= 1−y,从而PS=PQ.连接CS,则CS=CQ.所以, ΔCPQ∽= ΔCPS,ΔBCS∽= ΔDCQ.故
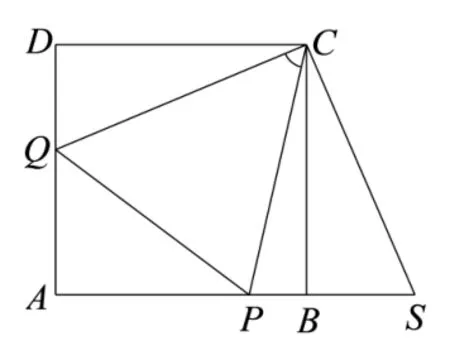
图3
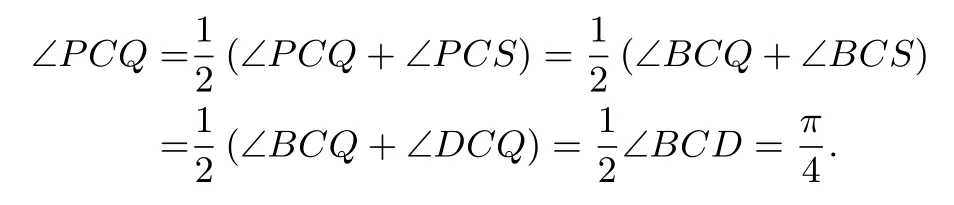
注1解法三说明,当ΔAPQ的周长为2 时,若过点C作线段PQ的垂线CR(垂足为R),则有以下三个结论成立:
结论1|CR|=1.
结论2 ΔPCQ是由ΔBCP与ΔDCQ分别沿CP与CQ翻折至边CB、CD重合而得.
结论3 点R分线段PQ所成比为
探究二ΔAPQ的周长为其他定值时,∠PCQ是一个定值吗?
设ΔAPQ的周长为n(0<n <2+则x+y+=n.变形可得
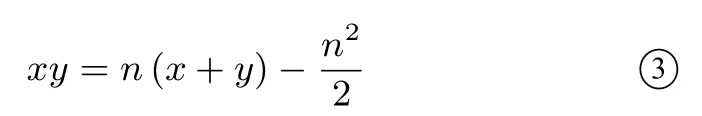
将③代入①, 得tan(α+β) =如果∠PCQ是定值,则解得n=2.故当且仅当ΔAPQ的周长为2 时,∠PCQ是一个定值.
探究三如何找出所有的周长为2 的ΔAPQ?
我们首先解决如下问题:当ΔAPQ的周长为2 时, 线段PQ上使得的点R的轨迹是什么图形? 建立如图4 所示平面直角坐标系,设R(x,y).由注1,R点是由ΔBCP与ΔDCQ分别沿CP与CQ翻折至CB与CD重合而得,且|CR|=1.不妨设Q(0,y0).则有
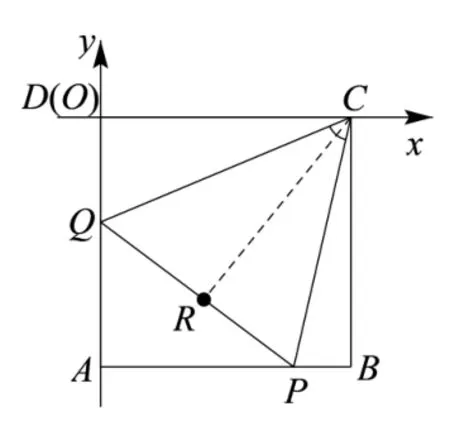
图4
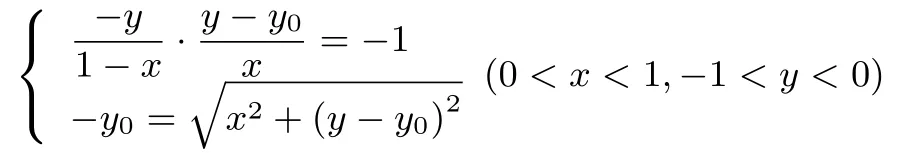
联立消去y0得点R的轨迹方程为(x −1)2+y2= 1(0<x <1,−1<y <0).故点R的轨迹是以点C为圆心,1 为半径的圆落在正方形内的部分(不含端点B和D).
下面,我们解决如何找出所有的周长为2 的ΔAPQ的问题.以点C为圆心,1 为半径作圆,记落在正方形ABCD内的圆弧为在圆弧(不含端点B、D)上任取一点R, 过点R作圆C的切线(或者过点R作与RC垂直的直线), 分别交线段AB、AD于P、Q两点, 则ΔAPQ即为所求.
探究四ΔAPQ的周长为2 时,ΔCPQ的面积的取值范围是什么?
由②,y=(0< x <1).PQ= 2−x −CR= 1.设ΔCPQ的面积为f(x).则f(x) =当x ∈0,2−时,f′(x)<0; 当x ∈时,f′(x)>0.所以,f(x) 在单调递减, 在单调递增.从而,当x=y= 2−时,ΔCPQ的面积f(x)取得最小值又因为f(x)<f(0) =所以,ΔCPQ的面积的取值范围是
注2如果探究四的问题改为: ΔAPQ的周长为2时, ΔCPQ的面积的最小值是多少? 则可以利用基本不等式求解.过程如下: 将xy≤代入②得,2(x+y)−2 ≤,化简得(x+y)2−8(x+y)+8 ≥0.由0< x,y <1 得,x+y≤ 4−所以,PQ=2−(x+y) ≥2−(故SΔCPQ=等号当且仅当x=y=2−成立.
探究五ΔAPQ的周长为2 时,ΔCPQ的周长的取值范围是什么?
我们先证明如下引理成立.
引理若m(x)是定义在区间D上的取值恒为正数的可导函数,则m2(x)与m(x)具有相同的单调性.
证明记M(x) =m2(x),x ∈D.则M′(x) =2m(x)·m′(x).因为m(x)>0,所以M′(x)与m′(x)同正负.故m2(x)与m(x)具有相同的单调性.
下面解决ΔAPQ的周长为2 时,ΔCPQ的周长的取值范围是什么的问题.
设ΔCPQ的周长为g(x),则
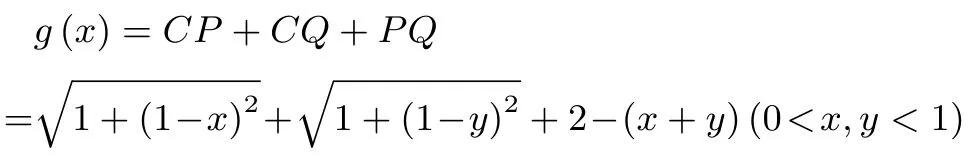
将y=代入,得g(x)=(0<x <1).记
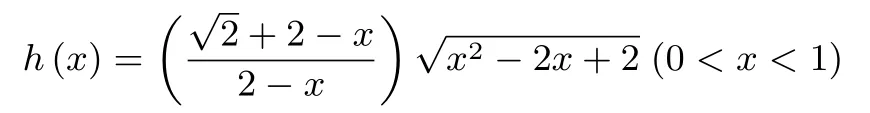
H(x)=[h(x)]2=(x2−2x+2)(0<x <1),i(x)=2−x −(0<x <1).因为h(x)>0,由引理,H(x)与h(x)具有相同的单调性.
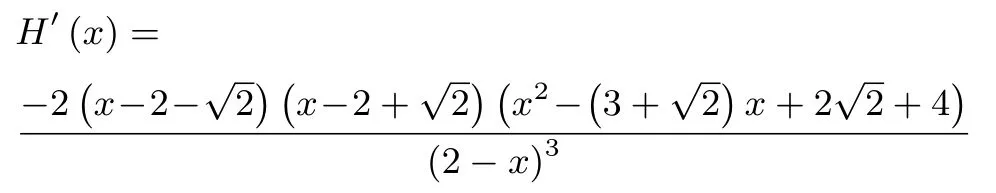
当x ∈时,H′(x)<0;当x ∈时,H′(x)>0.所以,H(x)与h(x)均在(0,2−单调递减,在单调递增.从而,当x= 2−时,h(x)取得最小值h(x)<h(0) =h(1) =+1.又由探究四可知,i(x) = 2f(x).所以, 当x ∈(0,2−时,i′(x)<0; 当x ∈时,i′(x)>0.故,i(x) 在单调递减, 在单调递增.从而, 当x= 2−时,i(x) 取得最小值i(x)<i(0) =i(1) = 1.所以, ΔCPQ的周长的取值范围是
一点感悟这一试题本是高中数学内容“三角恒等变换”下的一道复习参考题.在探究中却发现,它与平面向量、解三角形、平面几何、解析几何、函数与导数等内容都有联系.内涵之丰富实属预料之外.这给我们的高考复习提供了一种借鉴,即应当对教材习题做深入研究,探索其隐藏的问题、与其他内容之间的联系及蕴含的解题思想方法,让复习更为高效.

