基于多任务学习的风速实时预测方法

刘永前,周家慷,阎 洁,韩 爽,李 莉,Bekhbat Galsan

（1.华北电力大学 新能源电力系统国家重点实验室，北京102206；2.华北电力大学 新能源学院，北京102206；3.蒙古科技大学 电力工程学院，蒙古 乌兰巴托999097-15141）

0 引言

到2019年底，国内风电累计装机容量突破2.1亿kW，风电已经从补充能源进入到替代能源的发展阶段。然而，风能的间歇性、随机性和波动性，使高比例的风电并网会对电力系统的安全稳定运行带来严重威胁[1]。对风电场进行高精度的风速实时预测，一方面有助于电网做出最优调度决策[2]，另一方面有助于提高风电机组的运行状况和控制品质，使其在保证安全可靠运行的条件下充分利用风资源，促进风电场管理智能化。

目前，国内外对于风电场风速实时预测的研究越来越深入。风速的实时预测是一种超短期的多步预测，风速预测方法可大致分为物理方法、统计方法和组合方法。

物理方法依赖庞大复杂的气象数据和物理数据，计算量大，在超短期预测尺度上精度不够理想，且时间分辨率较大（小时级），一般不用于超短期预测。统计方法利用人工智能算法来建立历史输入数据与未来输出数据之间的关系，如时间序列算法[3]、支持向量机[4]、随机森林算法[5]和深度学习算法等。统计方法具备强大非线性拟合能力，适用于超短期风速预测，而单一预测模型可能受自身模型能力极限的限制而对潜藏信息挖掘不深入，进而捕获不到复杂的风速内在演变规律，致使模型泛化能力不强。组合方法是特征参数提取技术、数据相关度量化法、多种人工智能算法以及权值分配方法等各种方法及算法的排列组合[6]。与单个模型预测相比，组合方法可发挥各自模型的优势，在一定程度上提高模型对风速突变点的跟踪效果。

目前，许多组合方法以信号分析为基础，首先将风速分解为多个子序列，充分利用时序数据不同频率上的规律性，减小了预测误差。Yagang Z[7]采用变分模态将风速分解为非线性部分、线性部分和噪声部分，对非线性部分建立基于主成分分析的径向基核函数模型，对线性部分建立自回归滑动平均模型，对噪声部分进行概率分布拟合，进行确定性预测和不确定性预测。但是，这些以信号分析为基础的风速预测方法，在分解风速序列后，不同子序列各为独立的预测任务，忽略了各任务之间的相关性。

多任务学习，即假设现有若干个相关但不完全相同的任务，利用这些任务所包含的信息，辅助提升各个任务的性能。现有研究主要致力于多任务学习参数共享机制[8]和建立任务间的相关性[9]。在样本比较少的情况下，多任务学习能挖掘任务之间的关系，得到额外的有用信息且具有更好的模型泛化能力，使学习的效果更好。因此，将多任务学习方法应用于风速分解子序列预测，通过深度挖掘分享子序列预测任务间的信息，提升风速预测的效果。

在现有的相关研究中，超短期风速预测的时间分辨率大多为分钟级，难以满足高比例风电并网场景下风电场运行控制对预测精度和预测时间分辨率的要求。本文提出的风速实时预测方法属于秒级时间分辨率下的“极短期”预测，主要应用于风电机组控制。通过提前获知风速状况调整风电机组的控制策略，可提升风电机组发电量、减小机组疲劳载荷，同时也可进一步为电网在线优化调度提供更丰富的辅助信息。首先，进行风速序列分解，采用变分模态分解（VMD）将风速序列分解为一系列具有不同中心频率和有限带宽的信号；其次，建立多任务学习的共享层，使用长短期记忆神经网络（LSTM）提取风速子序列中的共享参数；然后，建立多任务学习的特定任务层，将共享参数与分解后的平稳信号作为输入，借助多个LSTM并行预测分解后的风速子序列；不同于一般的以信号分析为基础组合预测算法，本文所提方法采用多任务学习算法，考虑了各子序列预测任务之间的相关性，辅助提升各个预测任务的性能；最后，将多个预测结果叠加组合得到对原始序列的预测结果。

1 基于变分模态的风速分解方法

VMD原理包含构造变分问题和求解两部分。构造变分问题即将风速序列分解为k个具有中心频率和有限带宽的模态分量，根据L2范数约束，变分问题为各模态的估计带宽之和最小，满足各模态之和与原始信号相等，则相应约束变分表达式为

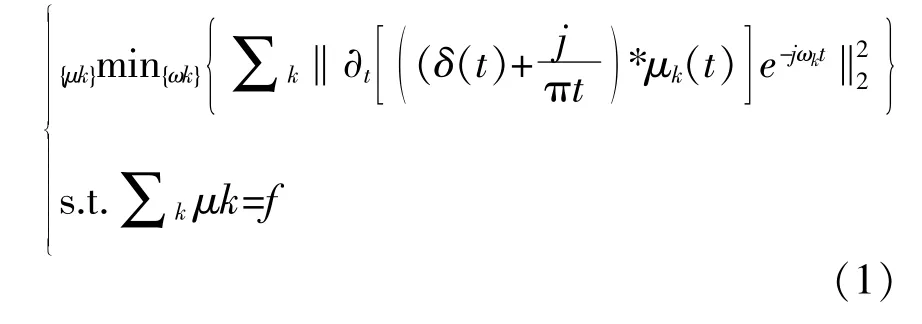
式中：k为模态数；{μk}为第k个模态分量；{ωk}为第k个模态分量对应的中心频率；δ（t）为狄拉克函数；*为卷积运算符；f为原始信号；t为时间；j为虚数单位。

求解式（1），引入拉格朗日乘法算子λ和乘法因子α，得到增广拉格朗日表达式。

分解模态个数k的选取对分解结果影响较大。为简化流程，减少模型运行时间及提高风速分解效率，本文通过计算末尾两个子模态分量与首端两个子模态分量的相对欧式距离百分比以判断其相似度，防止原始序列未被充分分解或被过度分解，从而合理确定k值。两子序列间的欧氏距离表示为

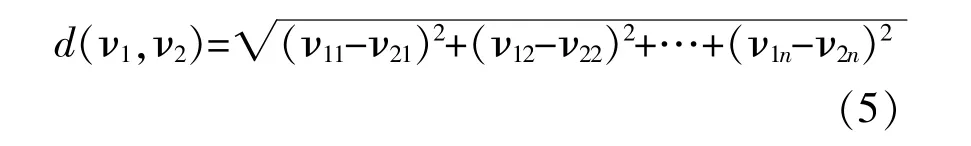
式中：ν1，ν2为两个序列；ν11，ν21的右下标第一个数为第i个序列，第二个下标为第i个序列的第j个数（i=1，2；j=1，2，3，…，n）。

首末两对序列的相对欧氏距离百分比为

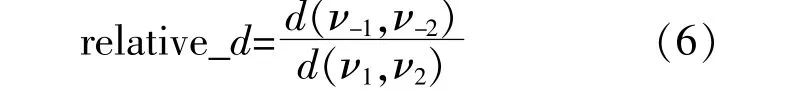
式中：ν-1，ν-2分别为倒数第一和倒数第二个序列；ν1，ν2分别为第一和第二个序列。

relative_d的阈值取5%±0.5%，大于该值时认为序列未被充分分解，小于该值时认为序列过度分解。文中风速时间序列数据取自中国某风电场，采样间隔为5 s，通过计算，当k=3时，relative_d=6.8%，不符合阈值条件；当k=4时，relative_d=4.9%，阈值符合条件。变分模态分解前后风速序列如图1所示。

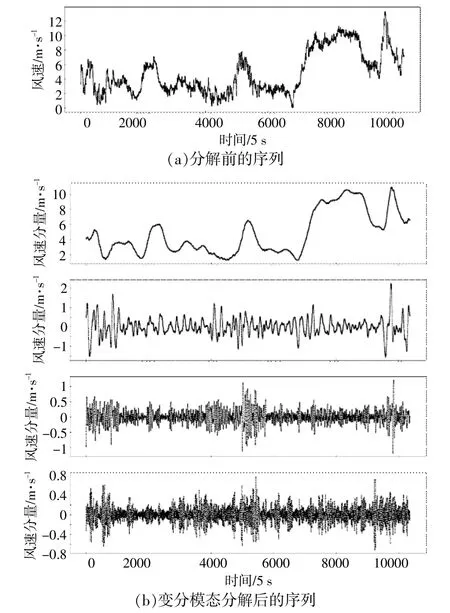
图1 变分模态分解前后风速序列Fig.1 Wind speed series before and after variational modal decomposition

2 基于多任务学习的风速实时预测

前文通过变分模态分解技术，将风速时间序列分解为k个子序列。本节将子序列的预测视为多个不同的任务，建立多任务学习模型，并通过长短期记忆网络对分解后的子序列进行预测。

2.1 长短期记忆网络

传统循环神经网络存在长期依赖问题，长短期记忆网络巧妙地利用“门”理论来改造循环神经网络，结构中包含遗忘门、输入门和输出门。LSTM单元在t时刻有3个输入：当前时刻网络的输入值xt，上一时刻LSTM的输出值ht-1，上一时刻的单元状态ct-1。LSTM单元在t时刻有两个输出：当前时刻的输出值ht，当前时刻单元状态ct。下标t为当前时刻，t-1为上一时刻。LSTM网络对输入xt处理最后生成输出ht的前向传播过程可分为如下6步，分别计算遗忘门ft、输入门it、写入单元的新信息c˜t、输出门ot和单元短时输出向量ht。

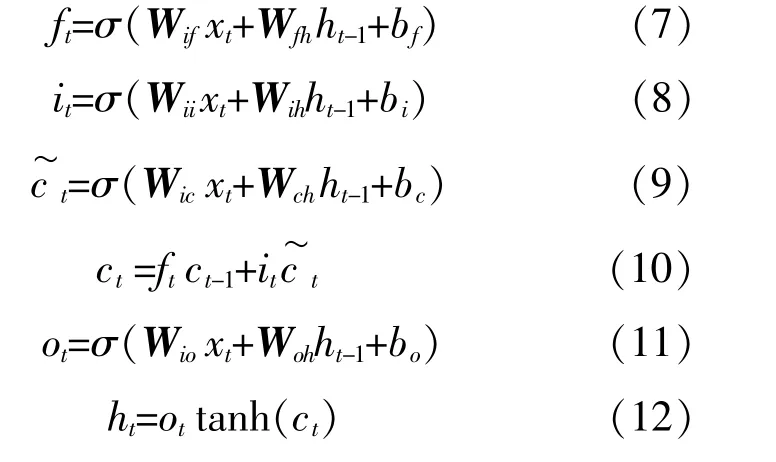
式中：Wif，Wii，Wic，Wio分别为当前输入与遗忘门、输入门、c˜t、输出门相乘的权重矩阵；Wfh，Wih，Wch，Woh分别为上一时刻输出与遗忘门、输入门c˜t、输出门相乘的权重矩阵；bf，bi，bc，bo分别为对应的偏置项；σ为sigmoid函数。

2.2 硬参数共享的多任务学习建模

多任务是相对于单任务而言，单任务学习（STL）是一次学习一个任务，并且各个任务间相互独立。对于非平稳、非线性的时间序列的预测则将其划分为一个个简单子序列，独立地对子序列进行预测，通过适当地加权组合得到原非线性序列的预测结果。然而，STL独立地对子序列进行预测往往忽视了子序列间的相互联系，不能充分利用序列之间有用信息辅助各子序列的预测。多任务学习（MTL）通过共享相关任务之间的表征以提高模型在目标任务的预测性能。

本文采用硬参数共享机制实现MTL模型，即靠近模型的输入部分为任务共享层，多个任务之间共享模型的若干层隐藏层，靠近模型的输出部分为任务特定层。硬共享的原理是不同的任务共享一个网络结构，不同任务之间的训练相辅相成，效果共同提升。

本文以LSTM为基本单元，构建基于参数共享的MTL模型。假设对所有子分量的预测视为是不同且相关的子任务，并把这些任务放在一起同时学习。MTL模型包括两个模块，用于提取共享参数的共享层和用于预测各子序列的特定任务层，其内部结构如图2所示。

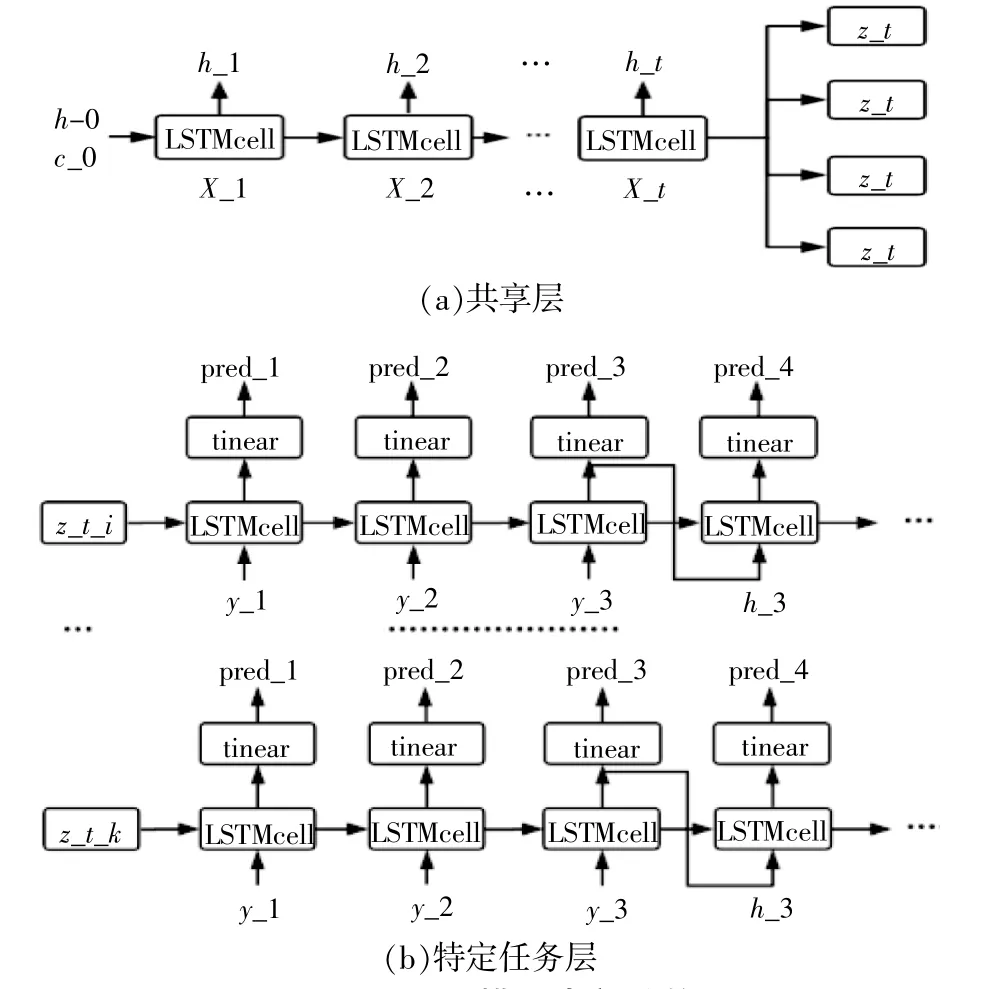
图2 MTL模型内部结构Fig.2 Internal structure of MTL model

由图2（a）可知，共享层的构建使用多个堆叠的LSTM将输入序列的特征提取到固定维度的张量中，完成共享参数的提取任务。结合上节内容可知，共享LSTMcell的输入是上一时刻的隐含状态ht-1以及当前时刻的输入，直到最后一个xt输入共享LSTMcell时，将最后的隐含层状态和单元状态作为整个原序列的表征张量。由于共享层与特定任务层要求数据形状一致，故通过复制拼接张量，完成共享参数表征从共享层到特定任务层数据传递。

由图2（b）可知：特定任务预测层的构建是利用从共享层传递过来的共享参数分别为每个子序列建立一个LSTM网络进行预测；最后将硬参数共享的多任务学习模型得到的各子序列的预测值进行叠加，得到最终预测结果。

3 算例分析

3.1 数据集描述及数据预处理

选取中国某风电场的风速时间序列数据，采样间隔为5 s，数据量为34 560，按6∶4划分训练集和测试集。模型的输入及输出数据如图3所示。

图3 数据窗口划分Fig.3 Data window division

图中input为输入的历史数据，output为要预测的目标序列，考虑到模型预测需要一定时间且时间分辨率小，预测输入的下一个点的意义不大，故在input和output间设置间隔interval，interval设置为5（即本文提出的模型及其对比模型均为提前25 s的多步风速实时预测）。在预测时，若变分模态将测试集的输入和输出一起进行分解，则会导致数据泄露，致使模型无法应用于实际。为此，我们将其分开分解，并采用0-1规范化对数据进行规范化处理。

3.2 结果与分析

为了验证所提模型的有效性及实用性，一方面设置经过变分模态分解和未经过变分模态分解的单任务模型预测进行结果对比（下文中分别简称为单任务模型和直接预测模型）；另一方面设置经过变分模态分解的单任务模型与所提多任务模型预测进行精度对比。每个模型都分别设置对风速提前25 s的10步预测模型及对风速提前25 s的5步预测模型。

采用两种误差指标，即平均绝对误差（MAE）和均方根误差（RMSE），来综合反映模型的预测精度。

本文提出的模型及其对比模型均为提前25 s的多步风速实时预测，所提模型均无须进行在线训练。在实际工程应用中，其预测模式为离线训练、在线预测、定期更新。在线预测是将实时数据输入训练好的模型进行预测。在上述系统配置下，该预测过程平均耗时为3 s，因此模型的时效性可以满足提前25 s的在线预测需求。

图4所示为MTL，STL和直接预测模型的对比实验结果。由图4可知，相比于STL和直接预测模型，MTL都能更好地追踪风速信号的变化趋势，特别是在风速剧烈波动时（图中段部分），而STL预测值偏小，直接预测模型预测值偏大。

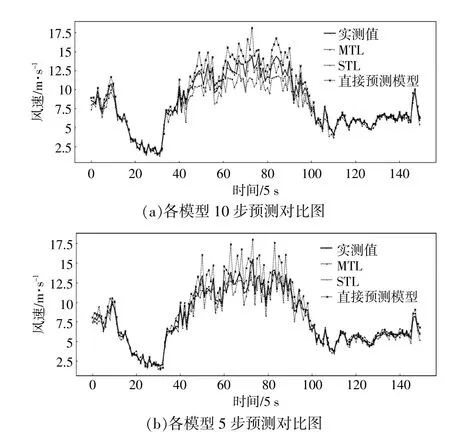
图4 各模型预测结果趋势对比Fig.4 Comparison of prediction results of models

各模型在10步、5步预测中各预测误差指标变化趋势如图5，6所示。由图5，6可知：STL在10步预测中的前7步和5步预测中的前4步RMSE和MAE均小于直接预测模型，结果表明了变分模态分解对风速实时预测精度提升的有效性；MTL在多步预测中各步RMSE和MAE均小于STL和直接预测模型，结果表明了MTL的应用可挖掘和分享子序列预测任务间的信息，提高了风速实时预测的精度。

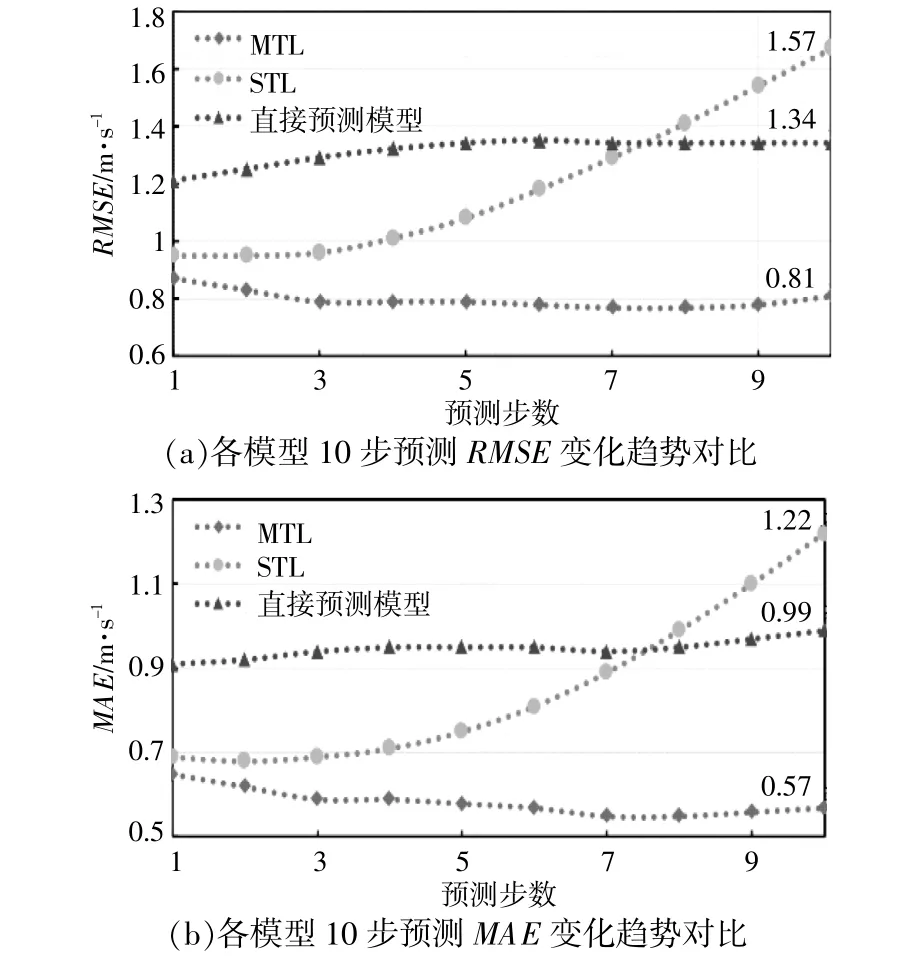
图5 各模型10步预测RMSE及MAE变化趋势对比Fig.5 Comparison of 10-step forecast RMSE and MAE change trends of each model

图6 各模型5步预测RMSE及MAE变化趋势对比Fig.6 Comparison of 5-step forecast RMSE and MAE change trends of each model

MTL，STL和直接预测模型的多步预测误差总体均值如表1所示。

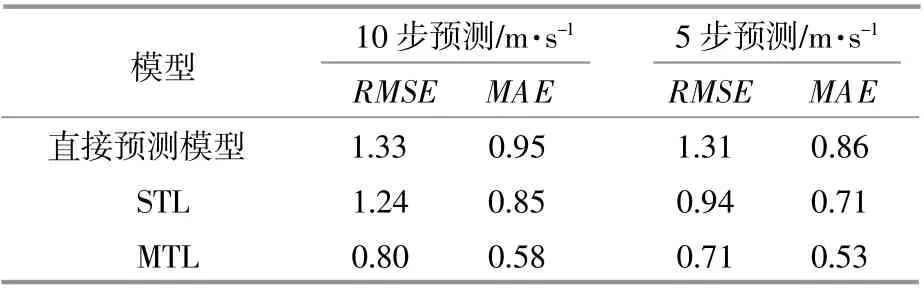
表1 模型多步预测误差总体均值Table 1 Multi-step forecast error overall mean of models

由表1可知：与经过变分模态分解和未经过变分模态分解的STL预测相比，MTL的RMSE总体均值在10步预测中分别降低了35.5%和39.8%，在5步预测中分别降低了24.5%和45.8%；MTL的MAE总体均值在10步预测中分别降低了31.8%和38.9%，在5步预测中分别降低了25.4%和38.4%。

针对不同风速进行算法的敏感性分析，各模型10步预测平均误差随风速变化趋势对比如图7所示。由图7可知：不同风速下，MTL优于STL，STL优于直接预测模型；从变化趋势来看，各模型的预测误差均随着风速的增大而增大，直接预测模型和STL在风速大于10 m/s时预测误差增大幅度远大于MTL，进一步证明了MTL在大风速多步预测中的优越性。

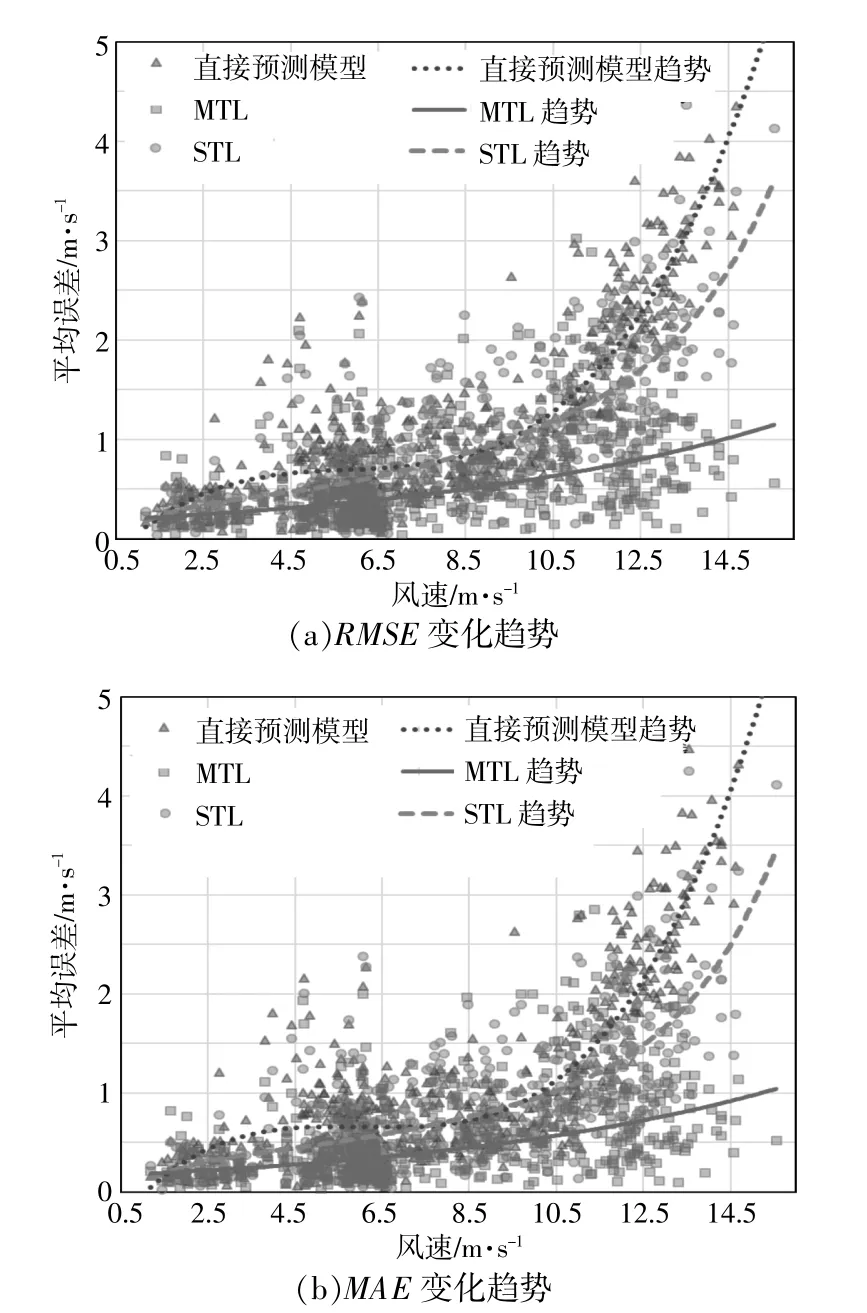
图7 各模型10步预测平均误差随风速变化趋势Fig.7 Comparison of the 10-step forecast average error of each model with the change trend of wind speed

4 结论

本文以时间分辨率为5 s的风速序列为研究对象，建立了基于多任务学习的风速预测模型。在风速预处理阶段，采用变分模态分解方法得到风速子序列。在风速预测阶段，结合LSTM建立基于参数共享的MTL，实现秒级风速实时多步预测。利用某风电场的实际风速数据进行算例分析，与经过变分模态分解的STL和未经过变分模态分解的直接预测模型相比，得到如下结论。

①STL在多步预测中的RMSE和MAE总体小于直接预测模型，表明了变分模态分解对风速实时预测精度提升的有效性。

②与STL和直接预测模型相比：MTL的RMSE总体均值在10步预测中分别降低了35.5%和39.8%，在5步预测中分别降低了24.5%和45.8%；MTL的MAE总体均值在10步预测中分别降低了31.8%和38.9%，在5步预测中分别降低了25.4%和38.4%。由此表明，将多任务学习方法应用于风速分解子序列预测，通过深度挖掘分享子序列预测任务间的信息，可大幅提高秒级风速实时预测精度。