计及分布式电源不确定性的多微网鲁棒博弈研究

姜明军,任明远,徐兰兰,孙旺青,刘晓峰

（1.国网甘肃省电力公司，甘肃 兰州730046；2.国网甘肃省电力公司 营销服务中心，甘肃 兰州730046；3.南京师范大学 电气与自动化工程学院，江苏 南京210023；4.东南大学 电气工程学院，江苏 南京210096）

0 引言

近年来，我国电力能源行业飞速发展，电网中风、光等分布式电源的接入比例不断提高，有效缓解了能源紧缺问题。为了提高可再生能源利用效率，通常以微网形式实现可再生能源的就地消纳[1]，[2]。微网一般由分布式电源、储能系统和负荷构成，可以在并网与孤岛模式下运行。然而，由于单个微网发展规模较小，供电可靠性低，因此往往将地域相邻的各微网互联组成多微网系统[3]，[4]。多微网系统不仅可以降低微网对大电网的依赖，增强供电可靠性，还可以促进分布式电源就地消纳，提升微网的经济效益。

现阶段，针对多微网系统调度优化问题的研究主要以系统运行成本最小化为目标构建调度模型，进而利用相关优化算法求解。文献[5]结合遗传与模拟退火算法求解微网全寿命周期成本与收益调度模型，可以在维持系统稳定的同时降低运行成本。文献[6]构建了微网群之间的主从博弈模型，有效提高了多微网的经济效益。文献[7]提出一种联合优化调度模型，上层以调度中心成本最小为目标，下层以各微网成本最小为目标，并设计了基于块坐标下降-不精确嵌套乘子法的求解算法，可以有效完成多微网的双层优化。

上述文献从不同方面开展对多微网系统的调度优化研究，却忽略了分布式电源出力的不确定性[8]～[10]。目前，已有学者对单个微网的不确定性展开了研究。文献[11]考虑了微网分布式电源和负荷的不确定性，采用Benders分解算法对所构建的不确定性优化模型进行求解，与改进的非支配排序遗传算法相比，其鲁棒性更优。文献[12]构建了计及分布式电源不确定性的微网调度鲁棒优化模型，并采用多阶段求解策略对其求解。文献[13]提出了一种模糊随机优化方法，为求解交直流混合微网调度的不确定性问题提供了新思路。文献[11]～[13]均以单微网为研究对象，均属于单主体决策的不确定性问题。多微网系统中存在多个微网，各微网分布式电源出力均存在不确定性，对整个多微网系统将产生重要影响。因此，开展多主体决策不确定性问题的研究，对于多微网系统的运行优化调度具有重要意义。

针对多微网系统分布式电源出力的不确定性问题，本文构建了以各微网运行费用最小为目标的非合作鲁棒博弈优化模型，从而可以解决计及不确定性的多主体决策问题。本文首先建立了多微网系统分布式电源、储能系统以及负荷响应模型；然后构建了各微网在非合作方式下的鲁棒博弈模型，并给出了求解方法；最后通过算例仿真验证了所提方法的有效性。

1 系统模型

本文所述场景如图1所示。多微网系统由N个微网组成，微网由风光分布式电源、储能系统和用户负荷构成，微网间可通过信息网络实现信息的交互。多微网系统控制中心负责用户负荷、电价等信息的收集与发布。

图1 多微网系统场景Fig.1 Scenario of multi-microgrid system

1.1 分布式电源模型

风光分布式电源既能满足用户负荷需求，也能在负荷低谷时段为储能系统充电，从而可以提升多微网系统的新能源消纳率，降低系统运行成本。微网n须要支付分布式电源发电费用，其费用表示为[14]

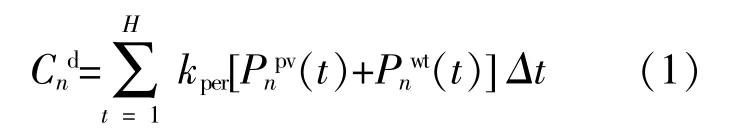
式中：kper为折算后的单位发电成本；Pnpv（t）为t时段微网n的光伏出力；Pnwt（t）为t时段微网n的风电出力；H为调度周期；Δt为各时段间隔。

1.2 储能系统模型

为了降低微网运行成本，储能系统在负荷低谷时段存储分布式电源的过剩电量，在用能高峰时为用户提供电能。微网须要支付储能系统日常运维费用，微网n储能系统在t时段内的费用Cnopt表示为[15]

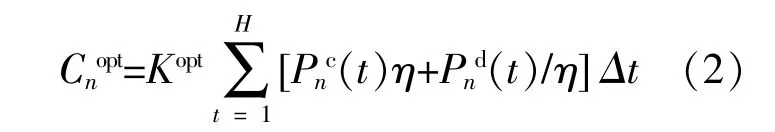
式中：Kopt为储能系统单位运维成本；Pnc（t）为t时段内的充电功率；Pnd（t）为t时段内放电功率；η为储能系统的充放电效率。

储能系统在运行过程中须满足以下约束：约束（3）表示储能充放电功率约束；约束（4）表示在一个调度周期的始末时刻剩余电量保持相等；约束（5）表示储能负荷状态约束。

1.3 用户负荷响应模型

用户负荷可以通过参与需求响应（DR）来实现资源的优化配置。用户负荷参与DR本质上不是为了减少负荷消耗，而是将可转移负荷转移至低谷时段。因此，用户负荷响应模型可表示为以下形式：

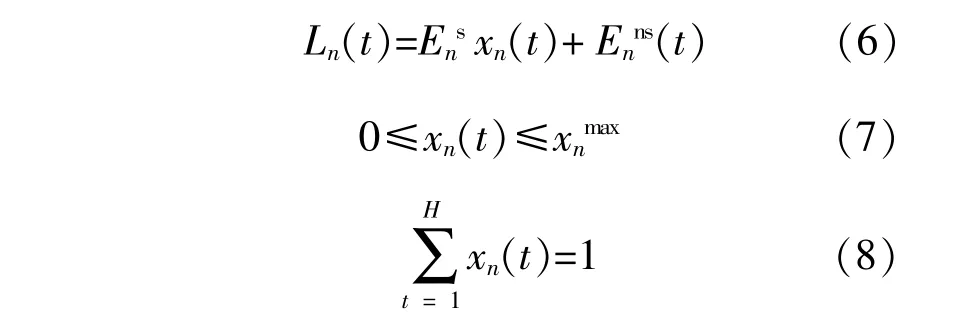
式中；Ln（t）为微网n参与DR后在t时段内的负荷需求；Ens为微网n可转移负荷总量；Enns（t）为微网n在t时段不可转移负荷量；xn（t）为微网n可转移负荷在t时段内转移比例；xnmax为可转移比例最大值。

1.4 微网能耗费用模型

在分布式电源无法满足用户负荷需求时，微网须要从公共电网购电。假设微网n在t时段内的购电功率为pnbuy（t），则多微网系统在t时段总购电功率为

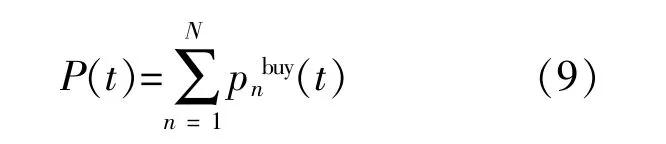
考虑到现阶段电网所采用的电价机制多为分时电价、实时电价等，本文假设微网和公共电网之间的市场交易以实时电价进行结算[16]。电价与负荷需求呈正相关，即需求越高，电价就越高。鉴于此，多微网系统在t时段总购电费用为

2 多微网系统鲁棒博弈

基于多微网系统中参与个体的趋利性，各微网首先考虑实现自身利益的最大化，因此存在着非合作博弈的竞争行为。非合作博弈不存在利益分配问题，尽管其产生的效益会不及合作博弈，但不会像合作博弈那样，一旦出现利益分配不均，就会导致合作联盟瓦解的问题。此外，各微网分布式电源出力均存在不确定性，给微网系统内部的能源调度带来了较大困难。本文基于鲁棒优化和非合作博弈理论，构建了多微网系统非合作鲁棒博弈模型，并基于列约束生成算法和强对偶原理，将模型解耦为主问题和子问题进行求解。

2.1 鲁棒博弈模型

微网日运行费用主要包括分布电源、储能系统的运维费用和向电网购电的费用；运行收益为反向售电收益。微网n日支出成本为

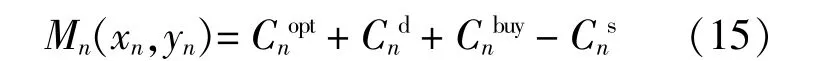
式中：xn为微网n日前DR负荷调度的决策向量，xn=[xn（1），xn（2），…，xn（H）]；yn为微网n的购电、售电、充电、放电的决策量，yn=[Pnbuy，Pns，Pnc，Pnd]。

在不考虑分布式电源出力不确定性时，上述多微网经济调度问题的确定性优化模型如式（16）所示。约束条件第1行对应优化模型中的不等式约束（3），（5），（7）；约束条件第2行对应优化模型中的等式约束（4），（8）；约束条件第3行对应优化模型中的功率约束（14）。

式中：χ（xn，un）为给定xn和un之后yn的可行域。

基于模型式（18），多微网系统非合作鲁棒博弈模型可建立以下形式：①参与者：所有微网用户；②策略集：各微网用户调度策略xn和yn；③收益函数：微网n参与博弈的收益Pn。

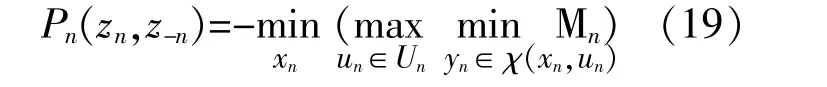
式中：zn为微网n的调度策略，zn=[xn，yn]；z-n为其他所有微网调度策略，z-n=[x-n，y-n]。

微网参与上述博弈的目标为实现自身利益最大化，当多微网系统中所有微网收益均达到最大，即博弈达到了均衡状态。该均衡状态称为Nash均衡：

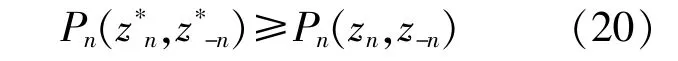
式中：（z*n，z*-n）为所构建非合作博弈模型的Nash均衡点。

2.2 模型转化

为求解非合作博弈模型Nash均衡解，须要对模型（19）进行转化。当微网n在求解自身最优策略z*n时，其余微网策略集z*-n可视为已知的常量。因此，对模型（19）的转化实际上就是对式（18）进行转化。因此，本文采用列约束生成算法，将模型（18）分解为主问题和子问题进行交替求解，进而得到原问题的最优解。根据列约束生成算法，式（18）分解后的主问题为

式中：M为足够大正数；Δun为微网n分布式电源出力预测误差向量；zn1和zn2为引入的连续辅助变量。

2.3 算法流程

经上述推导和转换，鲁棒博弈模型最终解耦为具有混合整数线性形式的主问题（21）和子问题（25），鲁棒博弈模型的求解算法如下。

将非合作鲁棒博弈模型（19）分解为主问题和子问题，并给定各微网初始场景u1，u2，…，un。设置调度方案成本上界UB=+∞，下界LB=-∞，迭代次数k=1，收敛阈值ε=10-3，多微网非合作博弈均衡解求解过程：

①初始化各微网策略zn与z-n；

②微网n根据当前场景un和其他微网策略集z-n求解问题（21），得到最优策略；

③根据微网n的最优策略，依次更新其他微网策略得到新的策略集z-n；

④返回步骤①，直至所有微网策略不再改变；

⑤根据微网总支出函数更新下界LB。

令k=k+1，返回步骤①。

3 仿真结果

为了验证本文所构建的多微网系统非合作鲁棒博弈优化模型的有效性，以N=3微网构成的多微网系统为例，求解出计及分布式电源出力不确定性的微网鲁棒调度计划及均衡解。

算例仿真主要参数设置如下。将1 d分为24个时段（H=24），各时段间隔Δt=1 h。根据负荷水平将1 d分为3个时段，即低谷时段（0：00-6：00和22：00-24：00）、平时段（6：00-17：00）和高峰时段（17：00-22：00）。低谷时段的a（t），b（t）分别为0.2和53；平时段的a（t），b（t）分别为0.3和111；高峰时段的a（t），b（t）分别为0.4和179。微网反向售电价格ks=37美元/（MW·h），储能系统运维成本Kopt=1.35美元/（MW·h）。最大充电功率限制Pcmax=0.7MW·h，最大放电功率限制Pdmax=1MW·h，储能系统充、放电效率均为92%。考虑到多微网系统在地理位置上相距较近，风光等资源条件近似，本算例假设各微网配置了相同容量的储能系统，而且分布式电源的出力相同。各微网负荷需求和分布式电源预测值和实际值如图2所示。

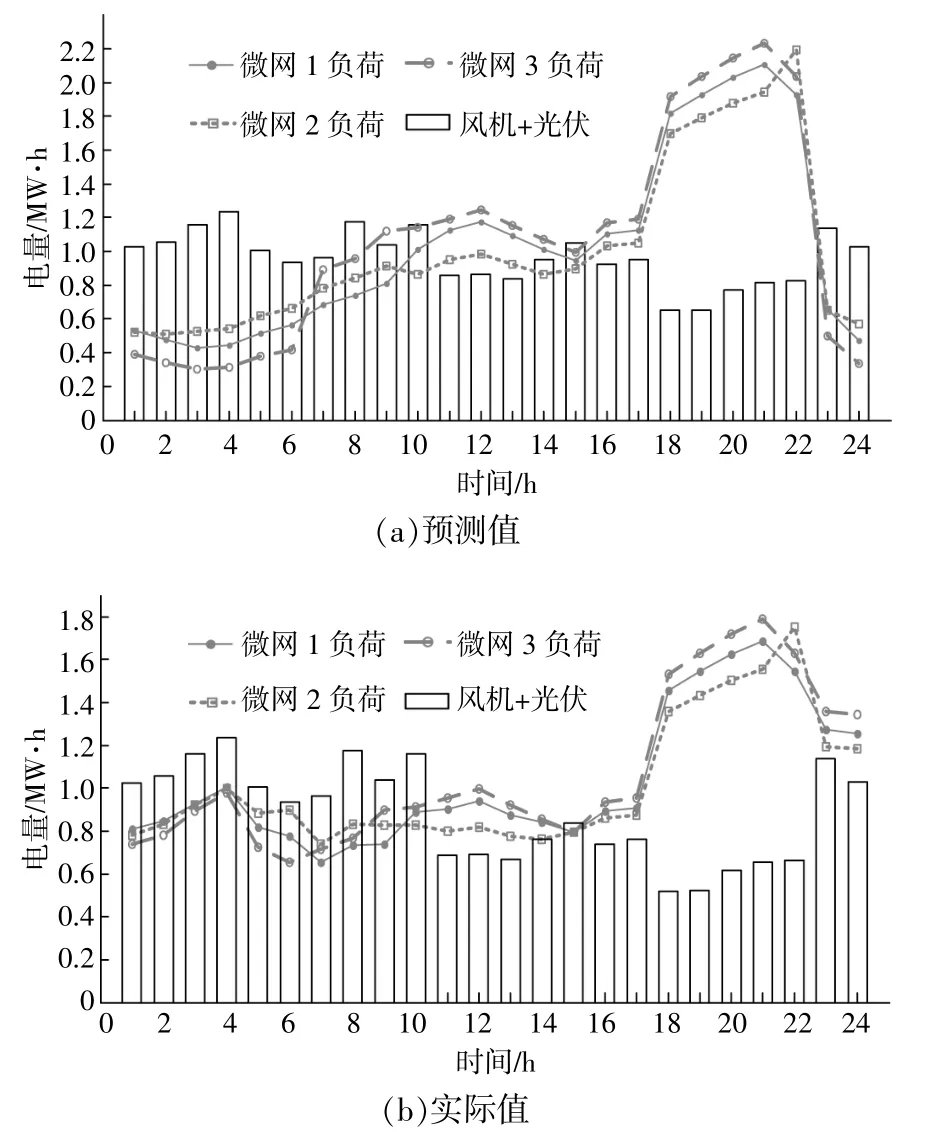
图2 微网负荷及分布式电源预测值和实际值Fig.2 Load distribution and predicted and actual values of distributed energy

3.1 多微网系统调度方案

基于以上参数，可以得到多微网系统优化调度方案。图3所示为多微网系统参与非合作博弈后的鲁棒调度优化结果。图中所示结果为微网可转移负荷占总负荷20%情况下的调度结果。从图3中可以看出，各微网主要在低谷时 段（0：00-6：00，22：00-24：00）从公共电网购电，从而降低购能费用；微网在低谷时段内未出现大量集中购电的行为，购电时间分布较为均匀，未对电网造成冲击；储能系统的充电行为主要集中在低谷时段，并在高峰时段（17：00-22：00）为微网负荷提供电能，可以进一步降低微网日运行费用。

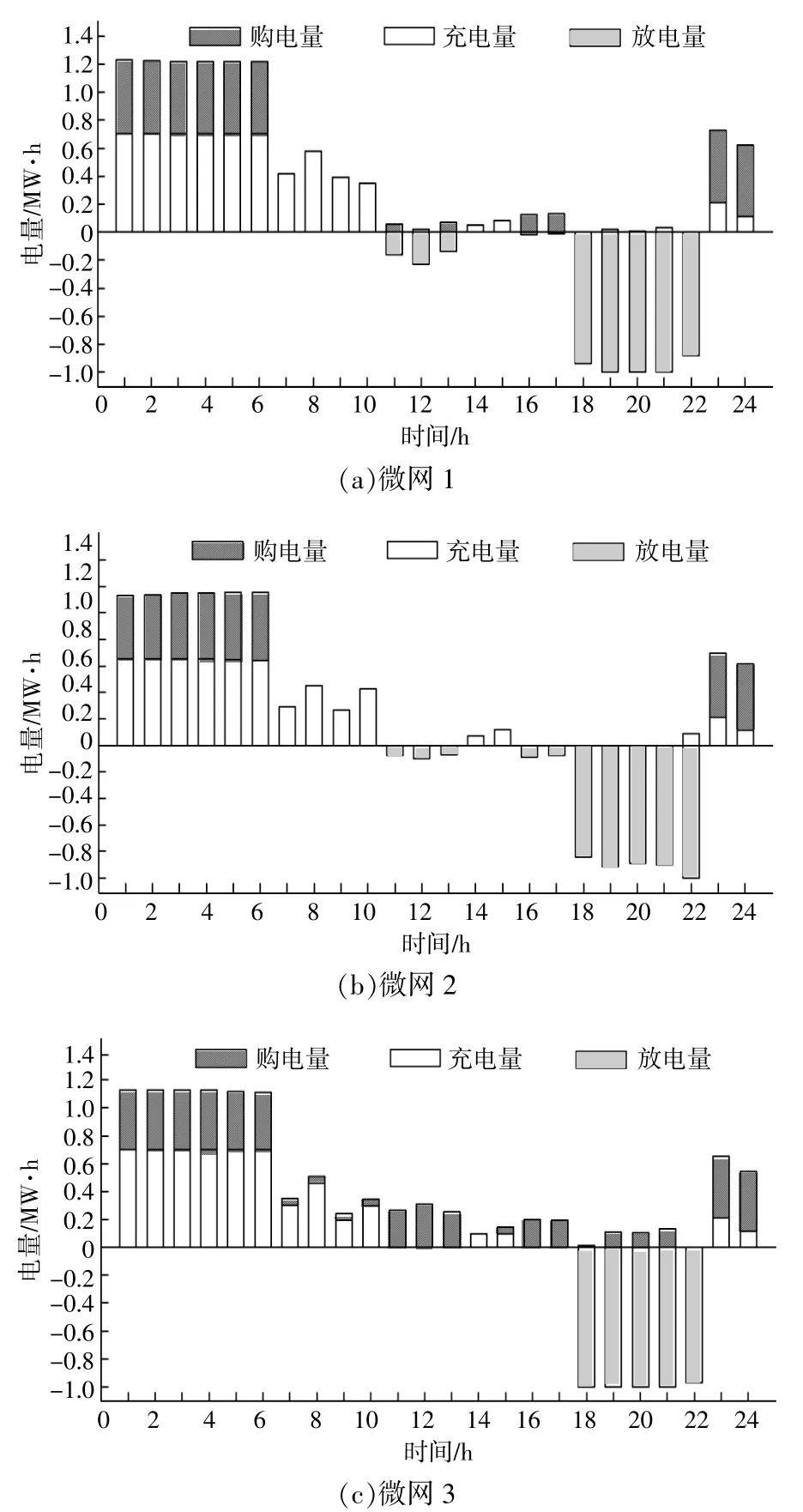
图3 非合作博弈鲁棒调度结果Fig.3 Robust scheduling results of non-cooperative game

微网可转移负荷占总负荷比重的大小对调度结果会产生较大影响。表1所示为多微网系统中可转移负荷占比分别为0%，20%，30%和40%时的调度结果分析。从表1可以看出，随着可转移负荷比例的增加，微网从公共电网的购电量呈现逐步下降的趋势，储能系统的充、放电量下降趋势较为明显。这主要是由于微网系统负荷总量没有改变，只是通过DR将负荷进行了转移。随着负荷不断从高峰时段转移至低谷时段，这些可转移负荷需求可直接由分布式电源来供应，所以无须储能系统频繁地参与调度，同时也减少向电网购电的电量。因此，随着可转移负荷占比的提升，多微网系统总费用也会逐步降低。

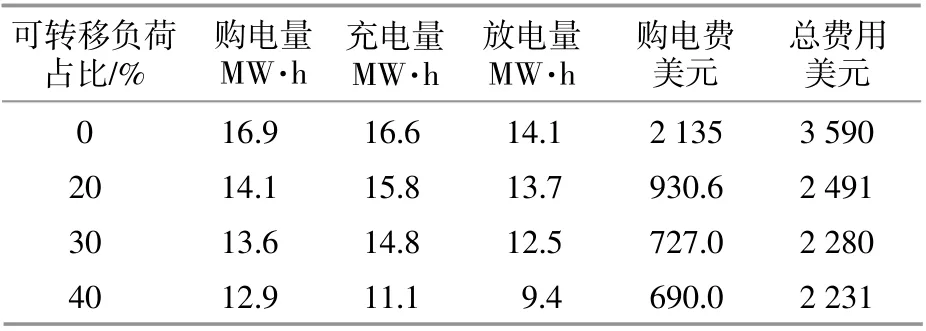
表1 可转移负荷对优化结果影响Table 1 The effects of shiftable loads on optimization result

表2分别给出了多微网系统参与优化前和参与鲁棒博弈时的费用对比（可转移负荷量均为20%）。从表2中可以看出，在微网参与调度优化后，从电网购电的费用下降了56.4%，总体费用下降了30.6%。多微网系统参与鲁棒博弈优化后，可以显著提高系统的运行经济性。

表2 多微网系统优化前后费用对比Table 2 Multi-microgrid's cost before and after optimization

3.2 优化模型对比

为了验证本文所提出的鲁棒博弈优化模型的有效性以及调度方案的保守性，对常规确定性模型和非合作鲁棒博弈模型进行了比较。

图4为微网2储能系统在两种调度模式下的调度安排。

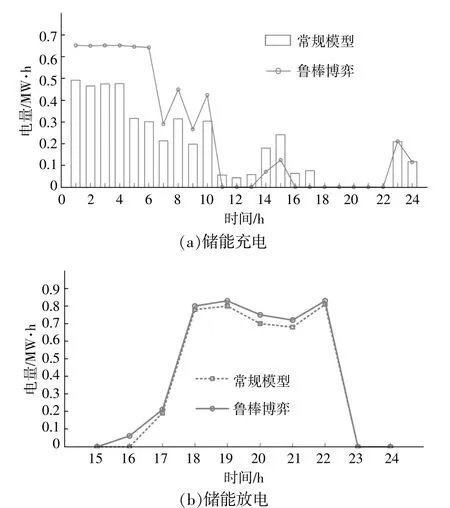
图4 两种调度方式储能充放电对比Fig.4 Charging/discharging comparison of energy storage under two dispatch strategies

由图4（a）可见，常规确定性模型中的储能在平时段的充电量要高于鲁棒博弈调度，在低谷时段的充电量要少于鲁棒博弈调度。这是因为鲁棒博弈得到的优化结果考虑了不确定因素，减少了在平时段的购电量，增加了在电价较低的低谷时段的充电量，降低了调度风险。

由图4（b）可见，为了应对分布式电源出力的不确定性，通过鲁棒博弈调度提高了储能调度的积极性，使其高于确定性调度模式，利用储能来降低分布式电源出力波动对系统的影响。鲁棒博弈总计放电量达到了4.7 MW·h，比确定性调度博弈（3.9 MW·h）增加了20.5%。

图5为不同保守度情况下的各微网储能充电策略对比。其中，场景1调节参数Γn=8，分布式电源出力最大波动为10%；场景2调节参数Γn=15，出力最大波动为10%；场景3调节参数Γn=15，出力最大波动为20%。从调度结果可以看出，当鲁棒调节参数Γn增加时或者分布式电源波动变剧烈时，储能会降低平峰时段的充电量，进而选择在低谷时段进行充电。这种更保守的行为可以避免在平时段因分布式电源出力不足而带来的能源短缺风险。

图5 3种场景下微网储能的鲁棒充电策略Fig.5 Charging strategy of energy storage under three different cases

为了验证本文所提出的调度方案的经济性，在分布式电源出力历史数据基础上，随机模拟了45组不同出力数据，来比较两种调度模式在应对分布式电源出力波动时的经济性。图6（a）、图6（b）、图6（c）分别对应Γn=5，Γn=10和Γn=15情况下的费用（分布式电源出力最大波动均为20%）。当预测精度较高时，即如图6（a）中的15组场景所示，确定性调度方案有更好的经济性。随着预测精度的下降，如图6（b）、图6（c）所示，鲁棒博弈的经济性要明显强于确定性调度方案。因此，决策者可以根据分布式电源出力预测精度来调节不确定性参数Γn，从而可以保证调度方案在具备经济性的同时，又具备一定的鲁棒性。

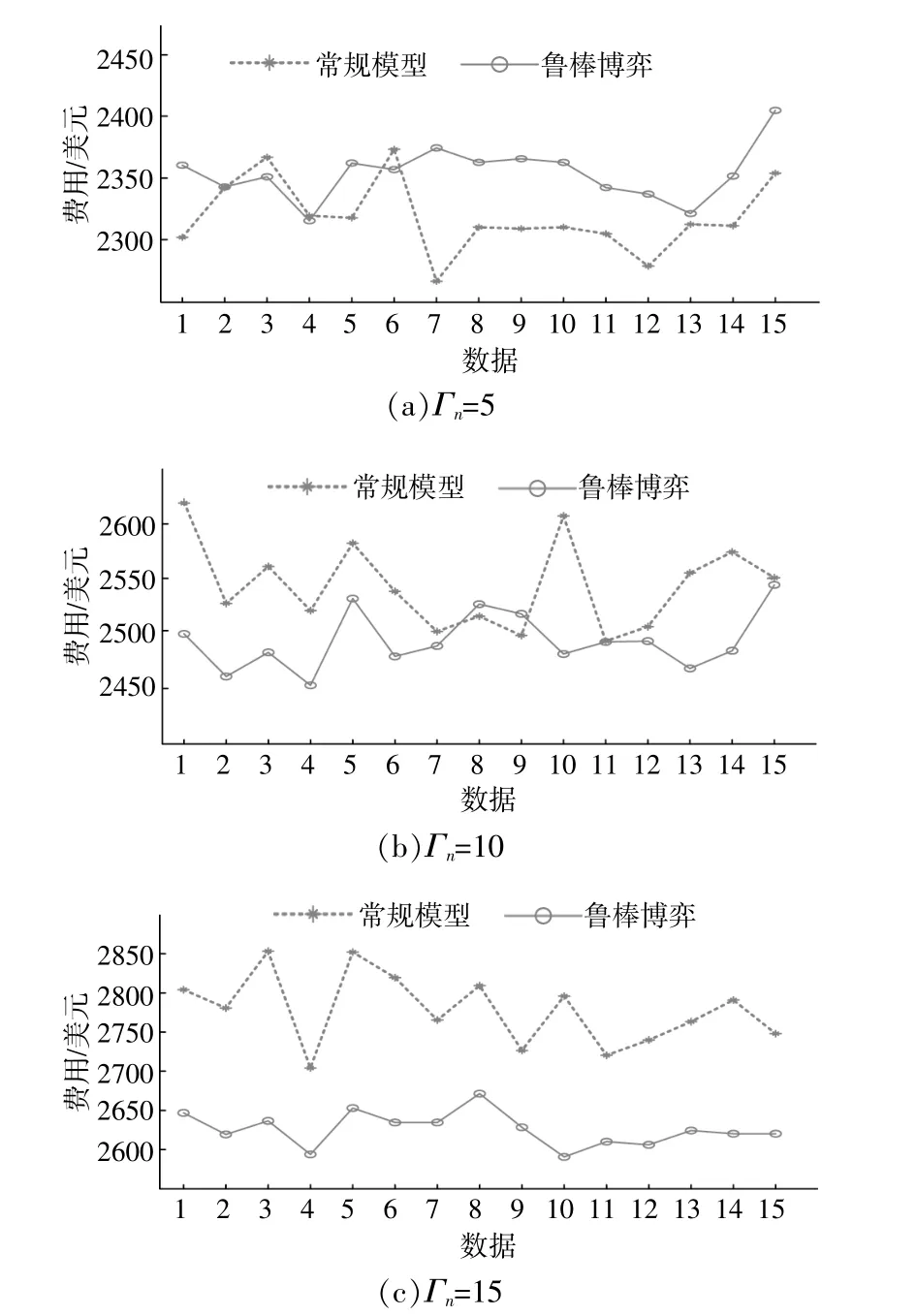
图6 不同出力下两种调度方式的经济性对比Fig.6 Economic comparison of two dispatch strategies for different energy output

4 结论

针对多微网系统分布式电源出力的不确定性问题，基于鲁棒优化和博弈理论构建了多微网系统非合作鲁棒博弈优化模型。

本文所提出的模型考虑了分布式电源的不确定性，通过对多微网鲁棒博弈模型的求解，可以得到各微网在非合作博弈模式下的鲁棒调度方案。

为了解决鲁棒优化过于保守的问题，所构建的模型中引入了不确定性调节参数，可以根据分布式电源出力预测精度来调节调度方案的保守性。

在分布式电源出力预测精度较高情况下，鲁棒博弈调度方案的经济性不及确定性调度方案；但随着预测误差的增大，鲁棒博弈调度方案的经济性逐渐优于确定性调度方案。