实时游戏中网络延迟对体验质量的影响

徐积文,张永棠,2

(1. 广东东软学院计算机学院，广东 佛山 528225; 2. 南昌工程学院江西省协同传感与先进计算技术研究所，江西 南昌 330003)

0 引 言

在网络实时游戏中，受网络延迟、延迟抖动和数据丢失等互联网服务质量（quality of service,QoS）的影响，将严重降低玩家终端的3D虚拟空间的体验感。

网络实时游戏可操作性与公平性的平衡关系引起了很多研究者的关注。例如，文献[1]使用3D虚拟空间中的硬对象研究网络延迟对公平性的影响。在3D虚拟空间中处理了一种网络化实时游戏，其中两个玩家通过操纵其触觉接口设备，试图用其对象（一个刚性立方体）竞争性地包含一个目标（一个球体）。评估结果表明，当玩家之间的网络延迟差异大于约30 ms时，玩家会感到不公平。同时，在文献[2]研究了在水果收获游戏中，两个玩家在3D虚拟空间中玩时，到达玩家所需的时间对公平性的影响。在游戏中，3D虚拟空间中所有的水果对象都是硬的。结果表明，当时间小于500 ms时，公平性几乎不受影响。

然而，在文献[1-2]中，由于仅研究了公平性，所以不清楚触觉接口装置的可操作性与玩家之间的公平性之间的关系。文献[3]提出要通过体验质量（quality of experience,QoE）评估来详细研究可操作性和公平性之间的关系，在该评估中，应该评估综合质量（即可操作性和公平性的加权总和）以检查哪个QoE具有对综合素质的贡献更大。此外，还应该分析每个终端应设置多少本地滞后，以保持尽可能高的综合质量。例如，如果公平性对综合质量的贡献较大，则如自适应 ∆因果控制，通过调整终端向时序最慢的终端输出时序，可以保持较高的综合质量[3]。然而，在目前的文献中，没有相关工作来研究网络延迟对QoE的影响，尤其是在虚拟环境中，对于软物体的可操作性和公平性。文献[4]仅对硬物体进行了研究，发现随着网络延迟的增加，物体变得越来越重。即，它们的特性由于网络延迟而改变。软物体的特性可能以与硬物体相同的方式改变；例如，随着网络延迟的增加，它们变得越来越难，但尚不清楚特性如何变化[5]。

本文构建了一个气球爆破游戏系统测试模型，通过玩家测试对软物体进行QoE评估，研究网络延迟变化实时游戏的影响，求解网络实时游戏的可操作性和的公平性的平衡。

1 测试模型描述

1.1 系统配置

气球爆破游戏的系统配置如图1所示。在三维虚拟空间中，两名玩家（玩家1和玩家2）各自用自己的触控笔爆破气球，两名玩家相互竞争爆破气球的数量。该系统由C1、C2两个终端组成，每个终端包含1台PC、1个触觉接口设备、1个显示器和1个耳机。每个终端的播放器使用触觉接口设备在虚拟空间中移动虚拟触控笔。当玩家用触控笔触碰气球时，通过触觉接口装置感知到反作用力，玩家能感受到气球的柔软。当玩家用触控笔推动气球时，气球会变形。如果玩家用力推气球，气球就会严重变形，气球就会爆裂消失。然后，玩家通过耳机听到爆裂的声音。

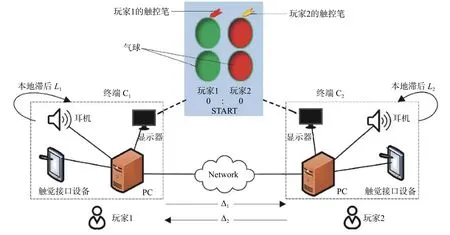
图1 气球爆破游戏的系统配置

1.2 游戏方法

在3D虚拟空间中有4个气球。玩家1在虚拟空间的左侧交替爆破2个气球，而玩家2在右侧爆破2个气球。此目的是为了避免在2个终端同时爆破同一气球。如果两个玩家都试图同时爆破气球，使用倒计时协议[6]确定哪个玩家比另一个用户更早爆破气球。在游戏开始之前，玩家可以通过将测针放置在各自的原始位置来做好准备（参见图2(a)）。当屏幕上显示“START”（开始）消息并发出蜂鸣声时，玩家开始爆破气球（参见图2(a)）。在游戏过程中，屏幕上会显示两个玩家的爆破气球数量（请参见图2(b)）。游戏开始后30 s，当屏幕上出现“GAME OVER”消息时，玩家停止游戏（见图2(c)）。蜂鸣器的声音还会提醒玩家此时停止游戏。一个气球爆破的玩家比其他玩家赢球；玩家2在图2(c)中获胜。当气球破裂并消失时，新气球会自动出现在破裂气球的位置。两名玩家都试图从气球的正面尽可能快速爆破各自的气球。

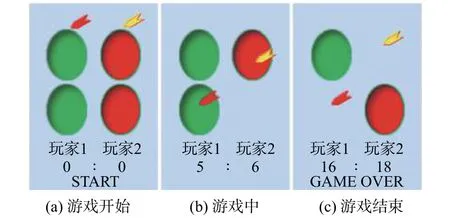
图2 虚拟空间图像

1.3 计算反应

施加到触觉界面上的反作用力由触觉渲染引擎生成，该引擎使用对象形状和材料属性（例如刚度和摩擦力）计算反作用力[7]。在图3中，绘制了4种情况下的反作用力、穿透深度和气球体积与爆破耗间的关系图。

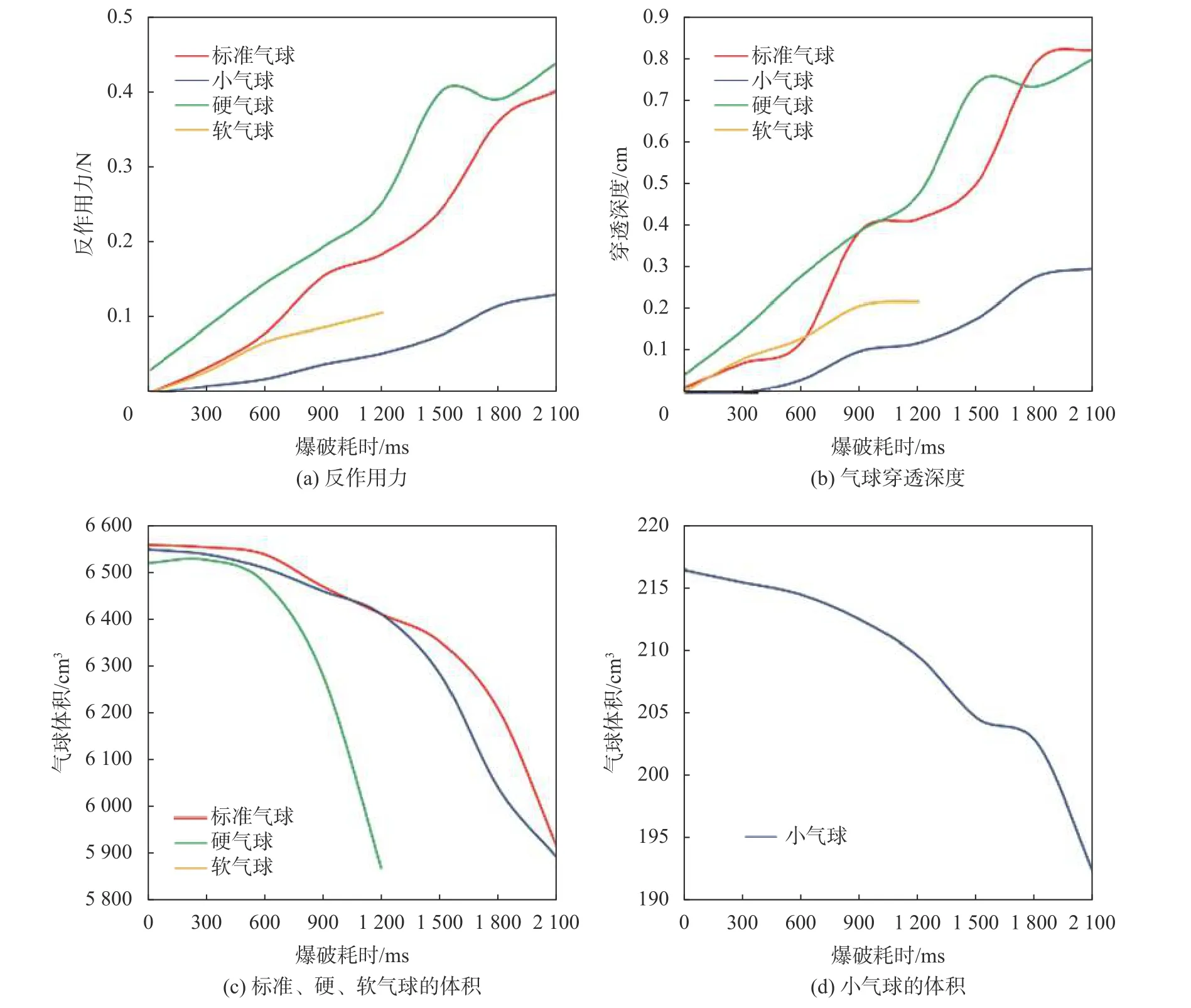
图3 气球反作用力、穿透深度与体积的关系

在标准球囊情况下，球囊三维轴（x、y和z）的半径分别为11 cm、15 cm和11 cm，其中假定触控笔测针的长度为10 cm。在小气球的情况下，使用半径分别为0.5 cm、1 cm和0.5 cm的气球。硬气球箱和软气球箱中的气球分别比标准气球箱中的硬或软两倍，气球的大小与标准气球箱的大小相同。爆破耗时被定义为从气球表面被触笔接触到气球破裂的瞬间之间的时间间隔。

在虚拟空间中，可以根据气球体积、触笔推动力两种方法判断气球爆炸。在本文的评估中，为了简单起见，使用了一种当气球体积达到阈值时气球爆裂的方法。当气球的体积小于阈值时，气球会爆炸。本文将阈值设置为气球初始体积的90%。

2 测试方案

将两个实验终端通过网络仿真器（NIST net）[8]相互连接，该仿真器用于代替图1所示的网络。网络仿真器为终端之间传输的每个数据包生成额外的恒定延迟。假设从终端 C1到 C2的恒定延迟为 ∆1，从C2到C1的恒定延迟为 ∆2。把 ∆1的本地滞后称为L1，∆2的本地滞后称为L2。在相同的延迟情况下，从C1到 C2的恒定延迟总是等于相反方向的恒定延迟。在不同的延迟情况下，从 C1到 C2的恒定延迟可以不同于相反方向的恒定延迟。

2.1 相同的延迟情况

在这次测试中，只研究了网络延迟对触觉接口设备可操作性的影响。没有研究玩家之间的公平性，因为当终端之间的网络延迟值相同时，公平性是完美的[9]。为了关注网络时延与触觉接口设备的可操作性之间的关系，在本例中只使用了 C1。将本地滞后称L1设置为与 ∆1相同的值。对16名年龄在20～30岁之间的玩家（男性和女性）进行了QoE评估。每名玩家在每次评估前将持续延迟设置为0 ms的条件下练习约2 min。在测试中，每名玩家交替击破位于虚拟空间左侧的两个蓝色气球。当气球破裂时，总会自动出现一个新的气球。为了研究网络延迟对不同类型气球的影响，使用第1.3小节中描述的4种气球进行了4次评估。根据气球类型，这种情况下的测试分别称为标准气球测试、小气球测试、硬气球测试和软气球测试。

在每次测试中，将每个玩家的延迟从0 ms随机顺序更改为500 ms，间隔为50 ms。测试顺序也按随机顺序为每个玩家选择。玩家用触控笔连续引爆气球30 s。每次触刺后，根据五级损伤量表（5. 不可察觉；4. 可察觉，但不令人讨厌；3. 稍令人讨厌；2. 令人讨厌；1. 非常令人讨厌）来判断是否容易爆裂。通过平均所有玩家的得分，得到了平均意见得分（mean opinion score，MOS）[10]。采用爆破气球的数量作为客观评价指标。每个用例的总评估时间约为每个玩家20 min。

2.2 不同的延迟情况

在这种情况下，进行了QoE评估，以明确网络延迟对可操作性、公平性和综合质量的影响。在评估中，两名玩家一起玩气球爆破游戏。评估前，每对玩家在延迟 ∆1=∆2=0 ms的情况下，玩3次气球爆破游戏，以适应游戏；也就是说，为这对玩家提供相同的条件。通过练习，每个玩家都知道如何使用触觉接口设备来爆破气球。在这种情况下，通过设置延迟 ∆1至0 ms或200 ms，设置延迟 ∆2至50 ms、100 ms、200 ms、300 ms或 500 ms进行评估。对16名年龄在20～30岁之间的玩家（男性和女性）进行了QoE评估。

将 ∆1设置为0 ms和200 ms的评估分别称为P1和P2。为了了解两个终端的本地滞后值对可操作性和公平性的影响，通过将本地滞后L1和L2设置为不同的值来进行评估。以50 ms为步长时间将L1从0 ms改为500 ms，将L2设为与 ∆2相同的值。在每次评估中，延迟和本地滞后的组合顺序是随机变化的。每次触刺气球需要30 ms。在每次触刺后要求玩家根据定义五级损伤量表（5. 听不清；4. 听不清，但不烦人；3. 稍微烦人；2. 烦人；1. 非常烦人）[11]，对可操作性、公平性和综合质量（即可操作性与公平性的加权和）做出判断。在每一次触刺中，如果两玩家在胜利或失败的结果上与练习中几乎相同，那么他们就会认为公平程度很高，并将得分定在5分。玩家给每次触刺打1～5分。通过对玩家的得分进行平均，得到了MOS。采用爆破气球的数量作为客观评价措施，每次评估的游戏总时间约为每对玩家2 h。

3 测评结果

对相同延迟和不同延迟两种情况分别做了100次评估实验，置信区间为95%。下面对测评结果进行分析。

3.1 相同延迟情况

图4(a)展示了4种评估的可操作性与延迟∆1的MOS值。由图可知，所有评估的MOS值都随着∆1的增大而减小。这是因为终端 C1的本地信息被缓冲了一段 ∆1的时间，因此，由于互动性降低，每个玩家都感觉气球越来越硬，越来越滑，很难把气球爆破。从图中还发现，当 ∆1≥100 ms时，小气球评估的MOS值小于其他情况。原因是，当延迟较大时，为了不从小气球上滑下，玩家操作触控笔比较困难。从图中可以看出，当 ∆1≤150 ms时，MOS值大于3.5。这意味着，对于小于或等于150 ms的网络延迟，QoE的恶化是允许的。

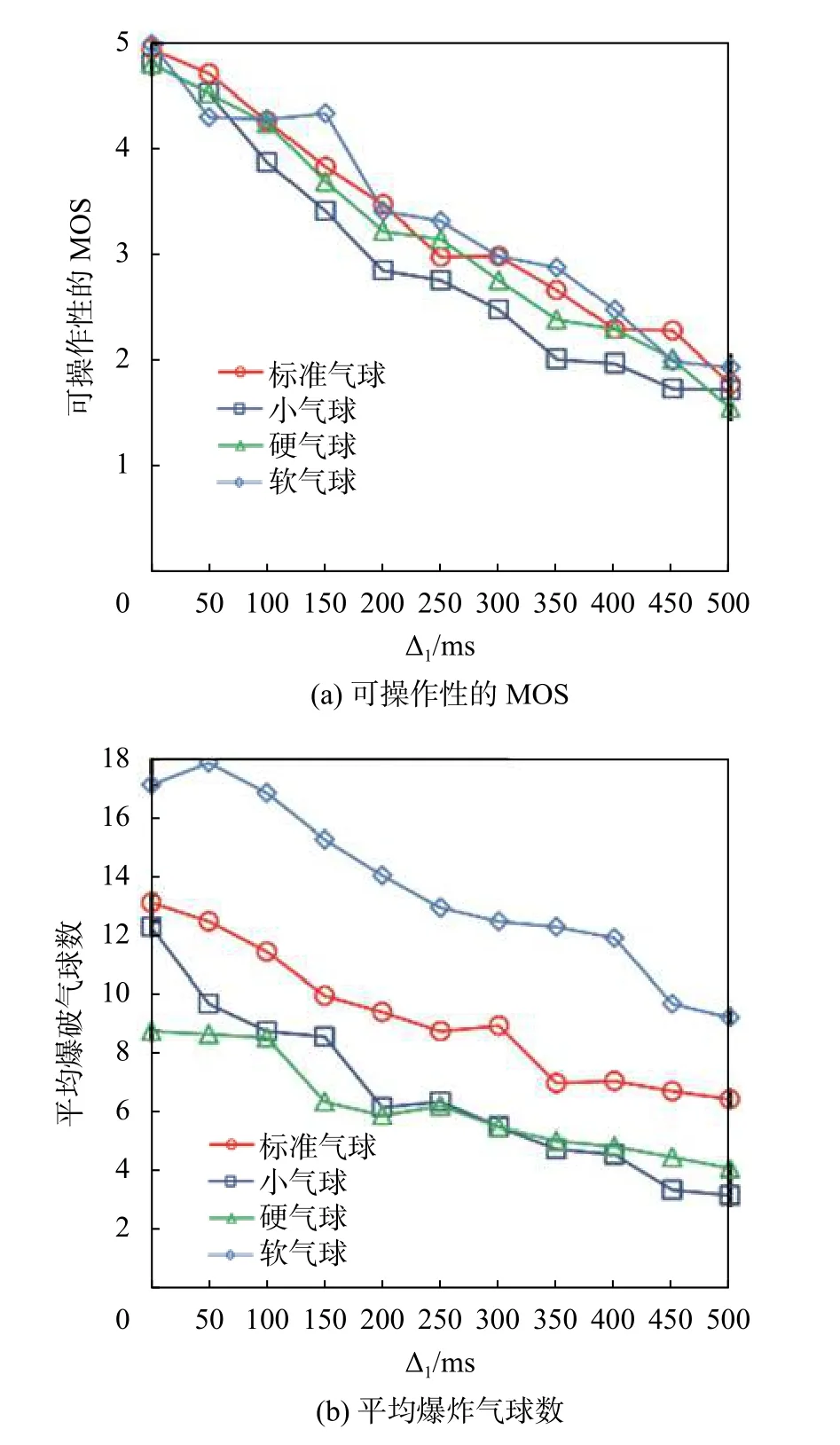
图4 相同延迟下4种气球的评价

图4(b)展示了爆破气球的平均数量与 ∆1的关系。由图可知，随着 ∆1的增加，所有评估中气球破裂的平均数量都变小。还可以看出，在软气球评估中，平均爆球数是最高的。在硬气球评估中，当∆1<250 ms时 ，爆破气球的平均数量最小；当∆1>300 ms时，小气球评估中爆破气球的数量最小。

3.2 不同延迟情况

3.2.1 主观评价结果

图5展示了终端的本地滞后与可操作性MOS值的关系。在图5(a)可以看到，在相同的延迟情况下,C1的所有 ∆2的可操作性MOS值都随着L1的增加而减小。这是因为 C1的本地信息缓冲时间为L1，因此，由于互动性降低，每个被测试用例都感觉气球越来越硬，越来越滑，很难把气球爆破。由图5(b)可知,C2处的MOS值与L1关系不大，主要依赖于∆2或L2。这是因为C2的本地信息被缓冲了一段时间的∆2。

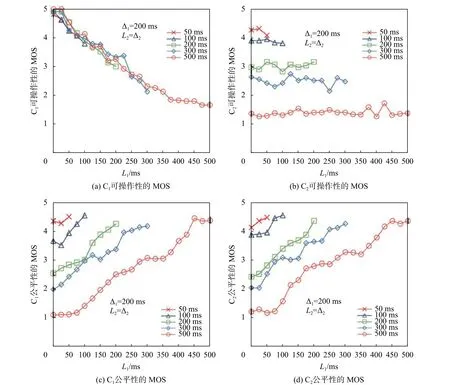
图5 不同延迟Δ2下终端的可操作性和公平性评价

在图5(c)和图5(d)中，注意到 ∆2所有值的公平性MOS值随着L1的增加而增加。这是因为当L1和L2的绝对差变小的时候，每个玩家都强烈地感到公平。

通过比较图5(a)和图5(c)，可操作性的MOS值与 C1的公平性之间存在权衡关系。也就是说，随着L1的增加，可操作性的MOS值变小，但公平性变大。此外，从图5(b)和图5(d)中可以看到C2的可操作性MOS值几乎没有变化，但公平性的MOS值变得更大。

为了求解两个终端本地滞后的最优值，计算了两个终端的平均MOS值，如图6所示。在图6(a)中可以看到，两个终端的可操作性的平均MOS值随着L1变大而减小。此外，还发现 ∆2=50 ms时，具有最高的MOS值；而 ∆2=500 ms时 ，对于L1的每个值具有最低的MOS值。在图中注意到，对于 ∆2的所有值，当L1变大时，平均MOS值增加。从两个终端的平均MOS值进一步证实了可操作性MOS值与公平性MOS值之间存在权衡关系。从图6(b)中还观察到，当本地滞后差的绝对值|L1−L2|≤ 75 ms时，MOS值大于3.5。因此，允许滞后的范围约为75 ms。这种本地滞后差的允许范围，可能有助于只关注公平性的网络应用。因此，将L1和L2分别设置为 ∆1和 ∆2的相同值，可以求得本地滞后的最优解为网络延迟绝对差的允许范围约小于或等于75 ms。

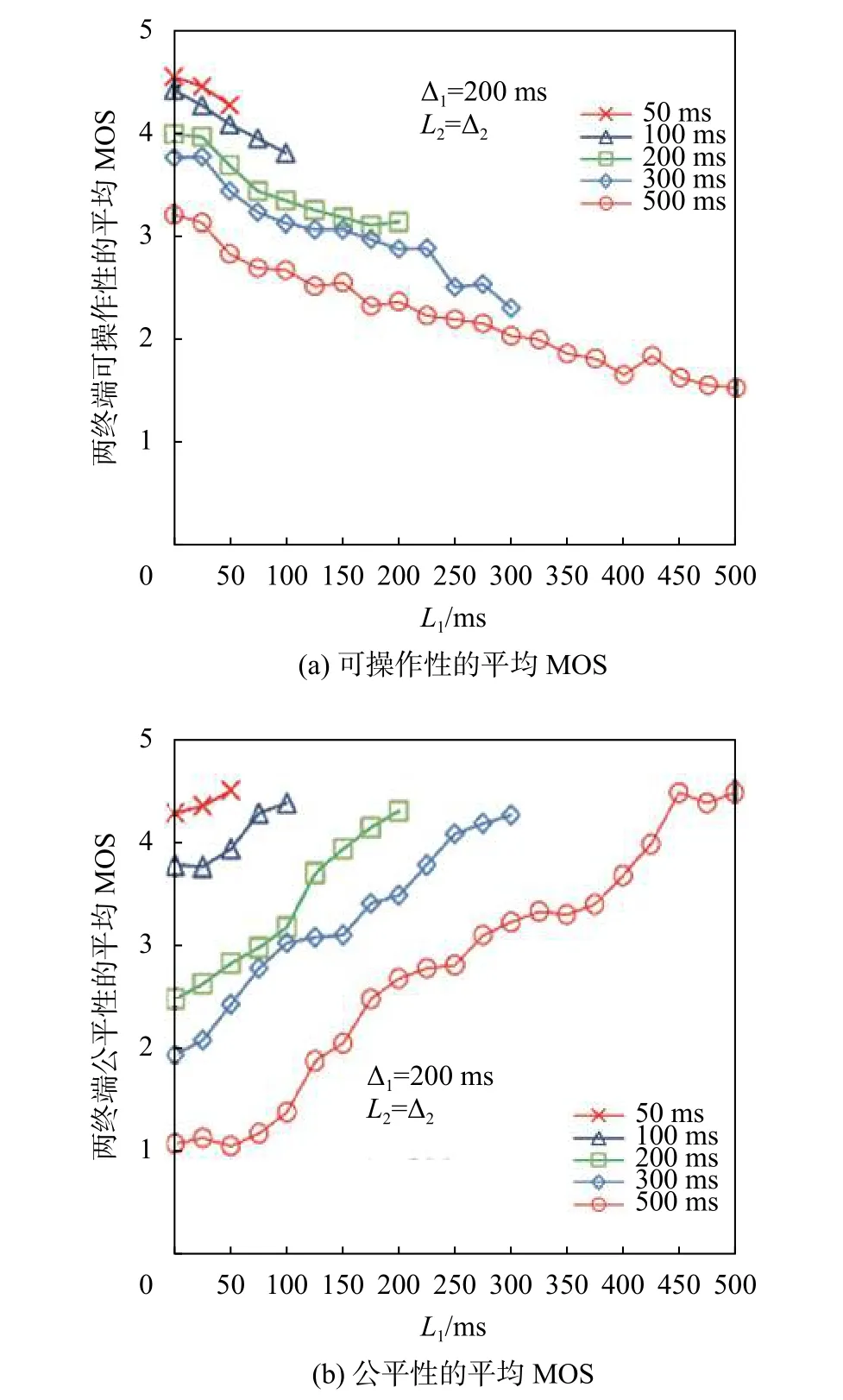
图6 不同时延Δ2下两终端间的评价

图7(a)和图7(b)展示了C1和C2的综合质量MOS值，图7(c)展示了综合质量的平均MOS值。从图7(a)可以看出,C1处 ∆2所有值的综合质量MOS值几乎不依赖于L1。在图7(b)中发现，当 ∆2为50 ms或100 ms时，MOS值几乎不依赖于L1。对于Δ2的其他值，MOS值随着L1的增大而增大。从图7(c)中可以看到，当 ∆2=50 ms时的平均MOS值几乎不依赖于L1。对于 ∆2的其他值，随着L1变大，平均MOS值趋向于略微增加。当 ∆2=100 ms时 ,L1的最佳值约为 75～100 ms。当 ∆2为 200 ms、300 ms或 500 ms时,L1的最佳值分别约为125～200 ms、225～300 ms或425～500 ms的范围内。

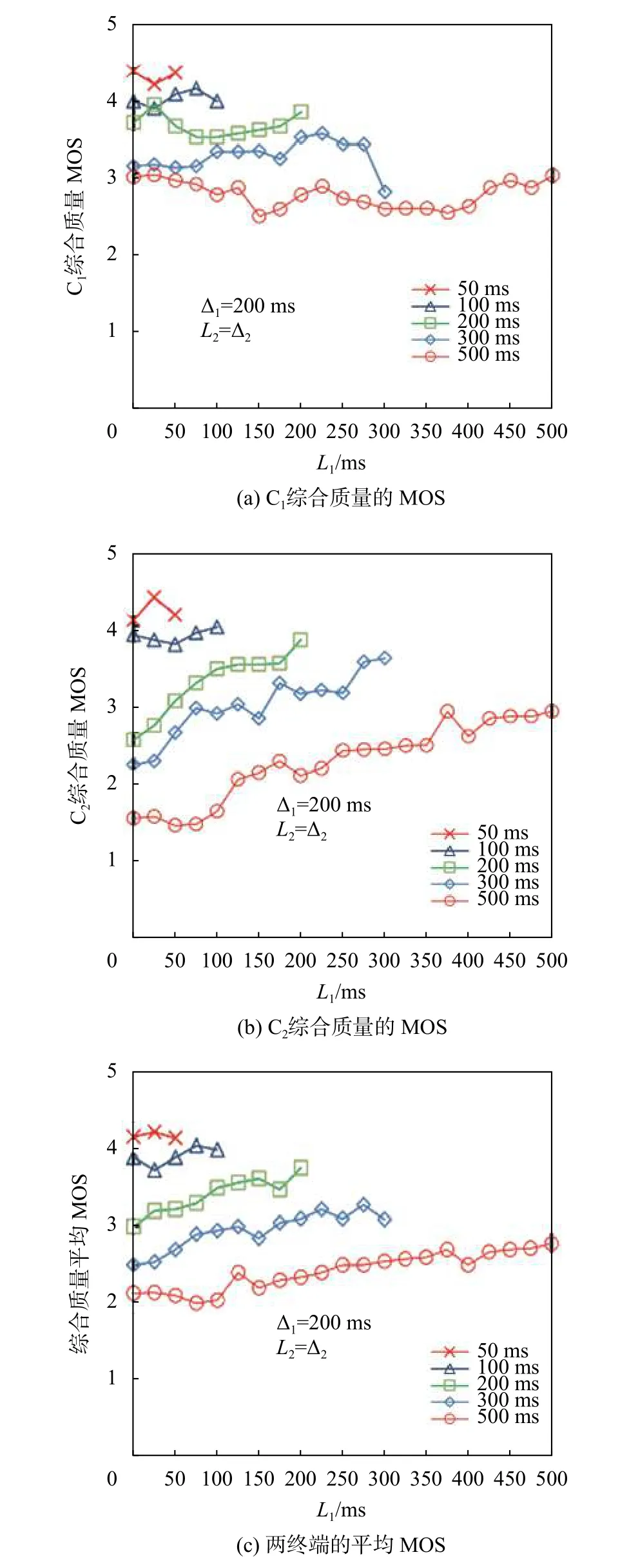
图7 不同延迟Δ2下综合质量评价

从图7(a)和图7(b)中，可以看出公平性的贡献大于可操作性对综合质量的贡献。从图7(c)中还可以看出，设置合理的本地滞后可以提升两个终端的综合质量。如果终端之间的网络延迟差约小于或等于50 ms，则L1和L2应分别设置为∆1和∆2的相同值。当差值约大于50 ms时，为简单起见，可以像自适应∆因果控制中一样，将本地滞后设置为终端之间网络延迟的较大值。

3.2.2 客观的评估结果

图8展示了 C1和 C2爆破气球的平均数量，以及爆破气球数量的平均差异，并且绘制了95%的置信区间。

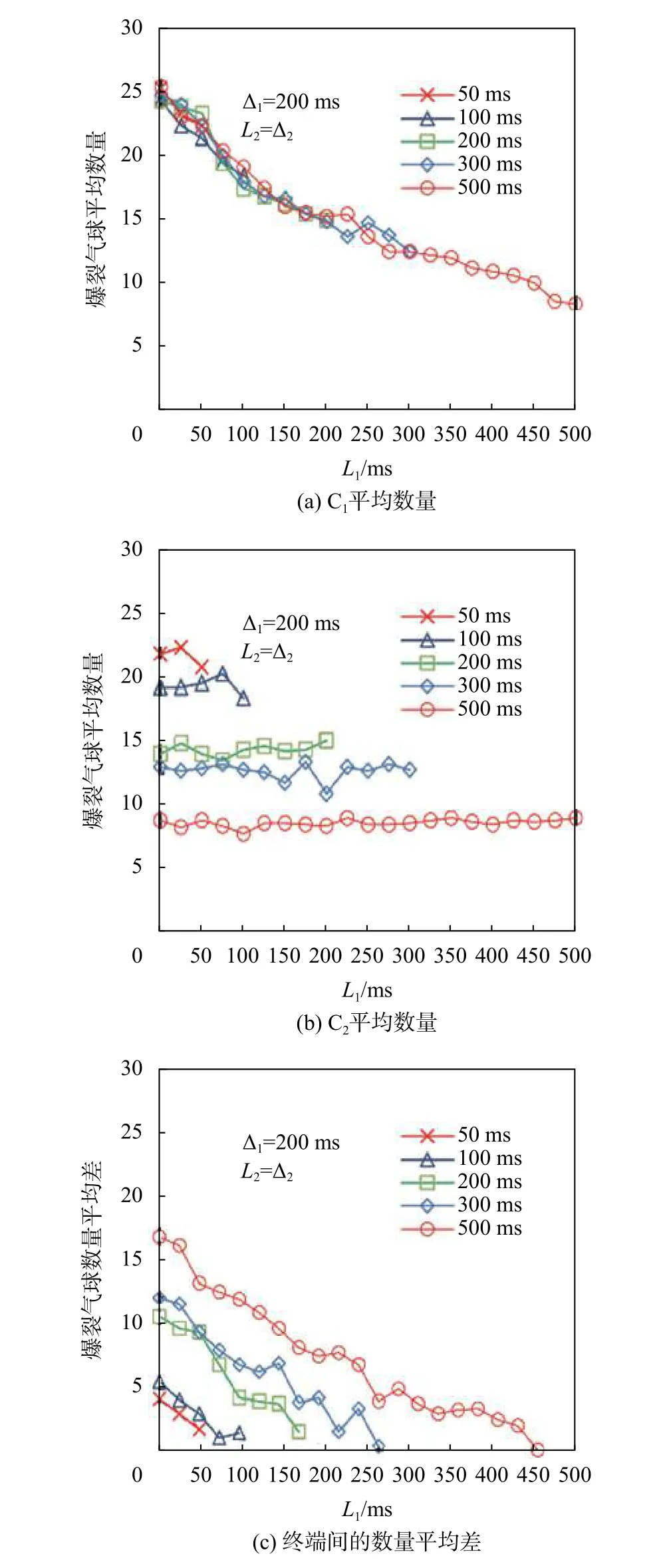
图8 不同延迟Δ2下爆破气球数量

在图8(a)中，看到 C1的平均爆裂气球数量随着L1的增加而减小。在图8(b)中，发现 C2的平均爆裂气球数量几乎不依赖于L1。通过将图8(a)和图8(b)分别与图5(a)和图5(b)进行比较可以得出，随着每个 ∆2的平均爆裂气球数量变小，可操作性的MOS值降低。图8(c)显示随着L1的增加，爆裂气球数量的平均差异变得更小。这是因为随着L1的增加，两个终端之间的本地滞后差变小。通过将图8(c)与图5(c)或图5(d)进行比较，看到曲线的趋势相反。也就是说，对于 ∆2的每个值，当爆裂气球数量的平均差最小时，可以获得最高的MOS值。

3.2.3 客观与主观结果的关系

通过比较客观结果和主观结果，发现它们相互关联。为了研究爆破气球的平均数量（或本地滞后）与可操作性的MOS值之间的关系，进行回归分析[12]，得到了两个评估的两个终端的估计方程（如表1所示）。在表中,OMOS表示可操作性的估计MOS值,Nburst是爆破气球的平均数量，∆是本地滞后,R2是根据自由度调整的贡献率，显示了与估计方程的拟合优度。由于表1中的贡献率很高，表明可操作性的MOS值可以从平均爆破气球数或本地滞后来估计，并且具有很高的精度。

表1 可操作性MOS的估计方程

此外，应用回归分析，研究了公平性的MOS值与爆破气球数量平均差的绝对值之间的关系，以及公平性的MOS值与本地滞后差的绝对值之间的关系。获得了两种情况下两个终端的方程（如表2所示）。在表中,FMOS是估算的公平性MOS值，DNburst是破裂气球数量的平均差,D∆是本地滞后差，贡献率R2很高。因此，可以根据爆破气球数的平均差的绝对值或本地滞后差的绝对值来高精度地估计MOS的公平性。同时，根据表3中所示的高贡献率，其中CMOS是综合质量的估计MOS值。

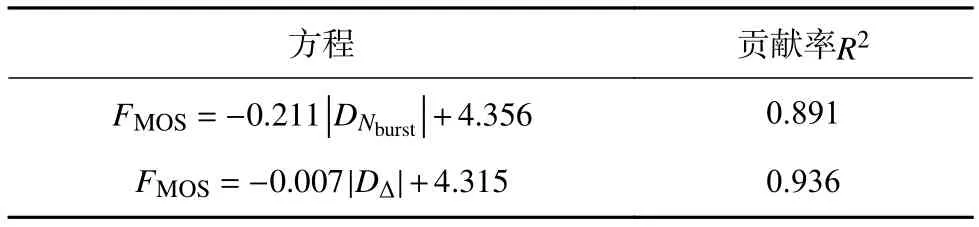
表2 公平性MOS的估计方程

表3 综合质量MOS的估计方程

此外，检验了两个终端的平均MOS值与客观结果之间的关系。可操作性平均MOS值的估计公式如表4所示，其中AOMOS是可操作性的估计平均MOS值,Nburst1是 C1的平均爆破气球数,Nburst2是C2的平均爆破气球数。从表中注意到，由于表中的贡献率R2很高，可操作性的平均MOS值在很大程度上可以从两个终端的爆破气球的平均数量来估计。还发现平均MOS公平值的估计公式与表2中的公式几乎相同。这意味着平均MOS公平值可以由爆破气球数的平均差的绝对值或本地滞后差的绝对值来实现高精度估计。综合质量平均MOS值的估算公式如表5所示，其中ACMOS是综合质量的平均MOS值,∆1是C1的本地滞后,∆2是C2的局部滞后。根据表5所示的高贡献率，综合质量的平均MOS值可以从两个终端的平均爆球数和爆球数平均差的绝对值，或者从两个终端的本地滞后来估计。

表4 可操作性平均MOS的估计公式

表5 综合质量平均MOS的估算公式

4 结束语

本文通过主观和客观的QoE评估，研究了在具有触觉的网络虚拟环境中，网络延迟对球囊爆破游戏的可操作性和公平性等QoE的影响。本文发现触觉接口设备的可操作性在很大程度上依赖于本地滞后。并且，可操作性取决于从本地终端到另一终端的网络延迟。可以观察到，随着网络延迟的增加，游戏中的软物体变得更硬、更滑。此外，验证了玩家之间的公平性取决于终端之间的网络延迟差异或终端之间的本地延迟差异。进一步证实了可操作性与公平性之间存在着权衡关系。可以通过在每个终端上设置本地滞后的值，实现可操作性和公平性的最优化。当终端之间的网络延迟的绝对差约小于或等于50 ms时，可以将每个终端的本地滞后设置为与从本地终端到另一终端的网络延迟相同的值。当差异约大于50 ms时，可以将本地滞后设置为终端之间较大的网络延迟值。

此外，还研究了主观和客观评估结果之间的关系。可操作性的MOS值可以由爆破气球的平均数或本地滞后来估计，具有较高的精度；公平性的MOS值可以由爆破气球数的平均差或本地滞后差的绝对值粗略估计。综合质量的MOS值可以从爆破气球的平均个数和爆破气球个数平均差的绝对值来估计，也可以在很大程度上从本地滞后和本地滞后差的绝对值来估计。

未来的工作将在爆破气球游戏中，对爆破气球的其他判断进行QoE评估。例如，当施加在气球上的力达到阈值时，气球可能会爆。还要将该结论应用到其他网络实时游戏中，确认可操作性和公平性之间的权衡关系，通过设置本地延迟确定两个终端的综合质量MOS值是否可以保持较高。这对未来互联网上网络实时游戏的研发具有一定的参考价值。