基于K-means聚类与概率神经网络的模拟电路故障诊断方法

李 楠,邓 威,王 晨,吴光辉

(1. 南京航空航天大学航空学院，江苏 南京 210016; 2. 中国商飞民用飞机试飞中心试飞运行部，上海 201323;3. 国防科技大学卫星导航研发中心，湖南 长沙 410073; 4. 中国商飞北京民用飞机技术研究中心，北京 102211; 5. 太原理工大学，山西 太原 030024)

0 引 言

目前，模拟电路已广泛应用于航空电子系统[1]。模拟电路的失效会影响航空电子系统的功能，引起系统故障，甚至引发坠机等安全事故。因此，模拟电路故障诊断在航空故障诊断领域得到了广泛关注，模拟电路故障诊断技术成为了航空电子系统安全稳定运行的重要技术保障，其有效实施可以快速准确地检测并定位电路的故障，减少系统带故障运行时间、停机时间以及维护成本，消除由于故障损伤的积累而带来的安全隐患。

为快速准确地实现故障诊断，特征提取与分类器算法相结合故障诊断技术在电网、电机、逆变器、模拟电路等对象上都得到了广泛的研究与应用[2-4]。针对模拟电路的软故障诊断问题，何怡刚[5]等人提出了一种随机算法、灵敏度分析、免疫遗传算法与神经网络相结合的软故障诊断方法，钟建林[6]等人通过构造描述特定电路状态的特征区间向量，提出了一种基于多频响应波形相似度的软故障诊断方法；针对模拟电路的特征提取问题，小波分形[7]、核判别分析[8]、小波包变换[9]、符号分析[10]、经验模态分解[11]、主成分分析[12]等特征提取技术被广泛应用于模拟电路的数据预处理过程；针对模拟电路诊断中传统测试性模型故障分辨率低的问题，朱敏等人[13]提出一种基于故障对布尔表的模拟电路测试性分析与故障诊断方法。针对容差模拟电路参数故障诊断问题，线性规划方法、系统搜索算法[14]、矩阵方程迭代算法[15]被用来求解最优的故障解集。针对模拟电路模型训练以及诊断效率低的问题，蚁狮算法[16]、粒子群优化算法[17-19]、遗传算法[20-21]等优化技术被广泛应用于模拟电路故障诊断模型的训练过程中。

在上述模拟电路故障诊断方法中，研究人员通常会将故障诊断问题转化为一个分类问题，通过设计高效、准确的分类器模型实现模拟电路的故障诊断。如最早一批将分类器技术用于模拟电路故障诊断的Aminian教授技术团队，他们基于神经网络进行模拟路故障诊断取得了大量的研究成果[22-23]。如支持向量机、k近邻、随机森林等智能分类器[24-25]被广泛用于模拟电路故障诊断，并取得了较好的诊断效果。

概率神经网络(PNN)作为一种神经网络分类器，具有学习过程简单、稳定性高、收敛贝叶斯最优解速度快等优点，基于PNN的故障诊断方法也被广泛应用于各种产品和系统中。相对于其他的分类器，PNN的可扩展性更强，可以根据诊断需求的不同，快速对诊断模型进行更新，特别适用于模拟电路故障诊断故障类型多的特点。然而由于概率神经网络模型中模式层神经元是影响故障诊断准确性和诊断效率的一个重要因素，传统的PNN方法采用所有的训练样本作为模式层神经元将导致诊断模型诊断效率低，故障诊断准确性不稳定等问题。

针对上述问题本文提出了一种基于K-means与概率神经网络的模拟电路故障诊断方法，通过新定义的聚类有效性指标确定聚类数量，采用K-means对同一故障状态下的训练数据进行聚类分析，剔除了训练数据中的离群点数据，以聚类分析得到的聚类中心作为模式层神经元样本，用于构建概率神经网络诊断模型，从而提高诊断模型的诊断准确性和诊断效率。

1 概率神经网络

概率神经网络是Specht博士于1990年依据Bayes准则，在径向基神经网络的基础上，提出的一种前馈型人工神经网络。该方法将Bayes概率理论与Parzen窗函数相结合，利用概率密度函数中的无参估计来进行Bayes决策，它将输入模式映射到相应的输出中进行分类。传统的PNN基本结构如图1所示，主要由四层构成：输入层、模式层、求和层和输出层。

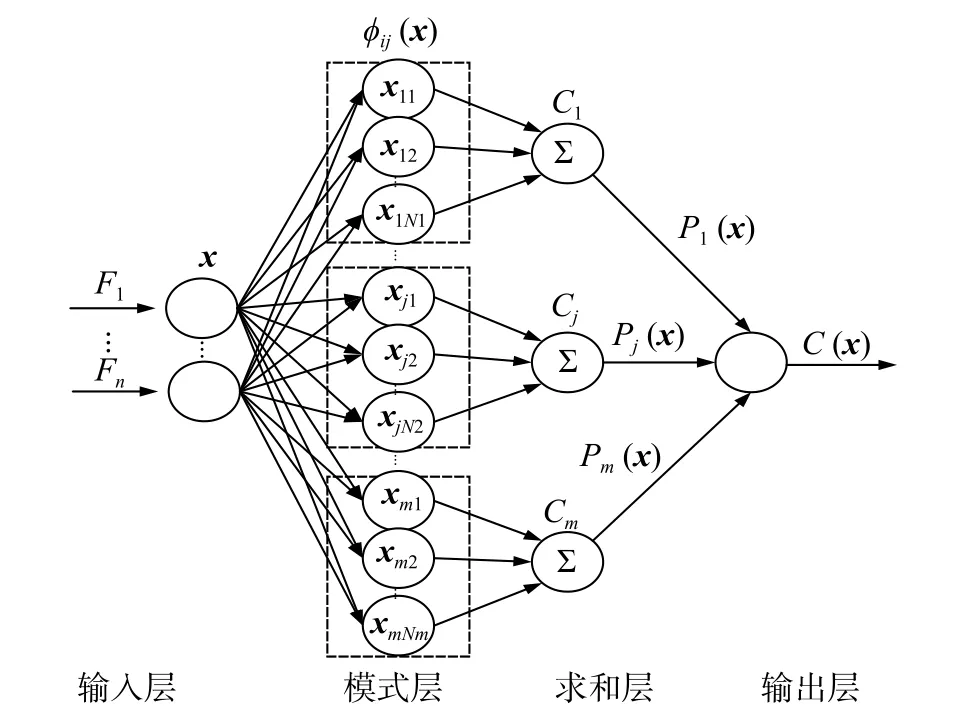
图1 概率神经网络基本结构

1) 输入层。输入层不执行任何计算，只用来对数据进行接收，接收到数据之后需要将其传输到模式层，其中，输入神经元的数目等于输入向量的维数。

2) 模式层。模式层用于计算输入向量与训练集中每个模式之间的匹配关系，训练样本的数量决定了模式层神经元的数量，在模式层中，神经元与训练样本一一对应。每个模式层的神经元在接收从输入层传递而来的数据后根据该公式计算，从而可以得到模式层的输出结果。

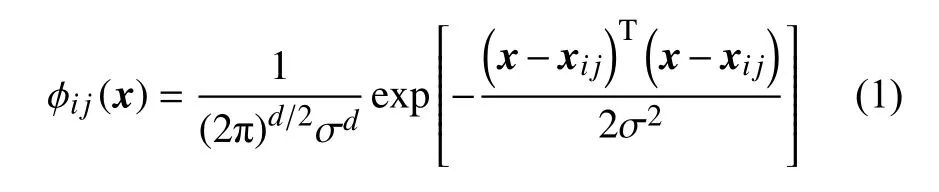
式中：σ——平滑系数；

x= [F1,F2,···,Fn]——输入向量；

xij——第j类的第i个模式层神经元向量。

3) 求和层。求和层中的一个神经元对应一种分类模式，求和层通过稀疏链接连接模式层。求和层神经元和模式层神经元连接的条件为它们对应同一个分类模式，通过对其输出值进行求和，该类别的最大可能性可以被求出。类别间的输出没有关系。计算公式如下：

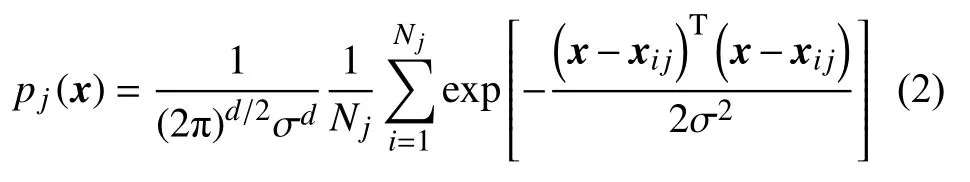
其中Nj为第j类样本总数。

4) 输出层。输出层根据贝叶斯决策规则选择后验概率最大的类作为分类结果，计算公式如下：

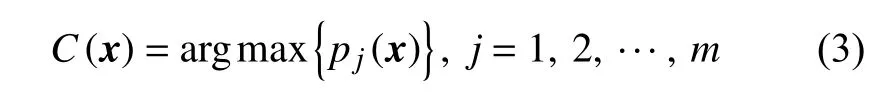
式中：C(x)——输入向量x的估计类；

m——类的总数。

2 K-means聚类分析

K-means算法是一种比较简单的无监督学习方法，最早是在1867年Macqueen最先提出来，该方法需要给定一个样本分类的个数K，然后将实现输入的N个数据按照一定的规则划分为K个聚类，使得所获的聚类中的对象相似度高，而不同聚类中的对象相似度低。该算法的核心思想是以空间中K个点为中心进行聚类，将最靠近它们的对象归为一类，通过不断的迭代计算，逐步更新各自的聚类中心。K-means算法描述如表1所示。

表1 K-means算法描述

K-means算法的具体流程如下：

1) 输入：K，DATA[N]；

2)选择K个初始的聚类中心，例如C[0]=DATA[0],···,C[K-1]=DATA[K-1]；

3)对 DATA [0 ],···,DATA[N]，分别与C[0],···,C[K-1]比较，如果与C[i]差值最小，i=1,2 ,···,K-1，则把该数据标记为Ci类；

4）对归为k类的点，重新计算聚类中心µk；

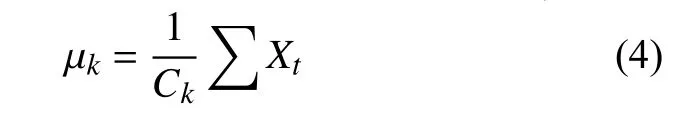
其中t为Ck的元素个数。

5）重复迭代，直到聚类中心变化不大为止。

在算法中选取欧氏距离作为相似性和距离判断的准则，计算每类中各点到聚类中心的距离平方和：

损失函数定义为：

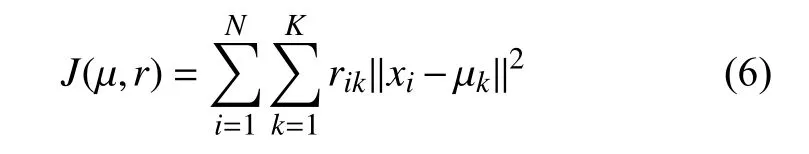
xi属于Ck类时，rik=1；xi不属于Ck类时，rik=0。

3 基于K-means与概率神经网络的诊断方法

3.1 基本原理

基于K-means与概率神经网络的诊断方法的流程如图2所示，主要包括模型训练与故障诊断两个过程。首先需要收集、获取电路各个状态下的数据，将其按比例划分为训练样本数据与验证样本数据，针对训练样本数据，采用基于K-means聚类的模式层神经元优选算法对训练样本数据进行筛选处理，获得最终的模式层神经元样本，根据优选后的训练样本构建概率神经网络诊断模型，实现故障诊断。

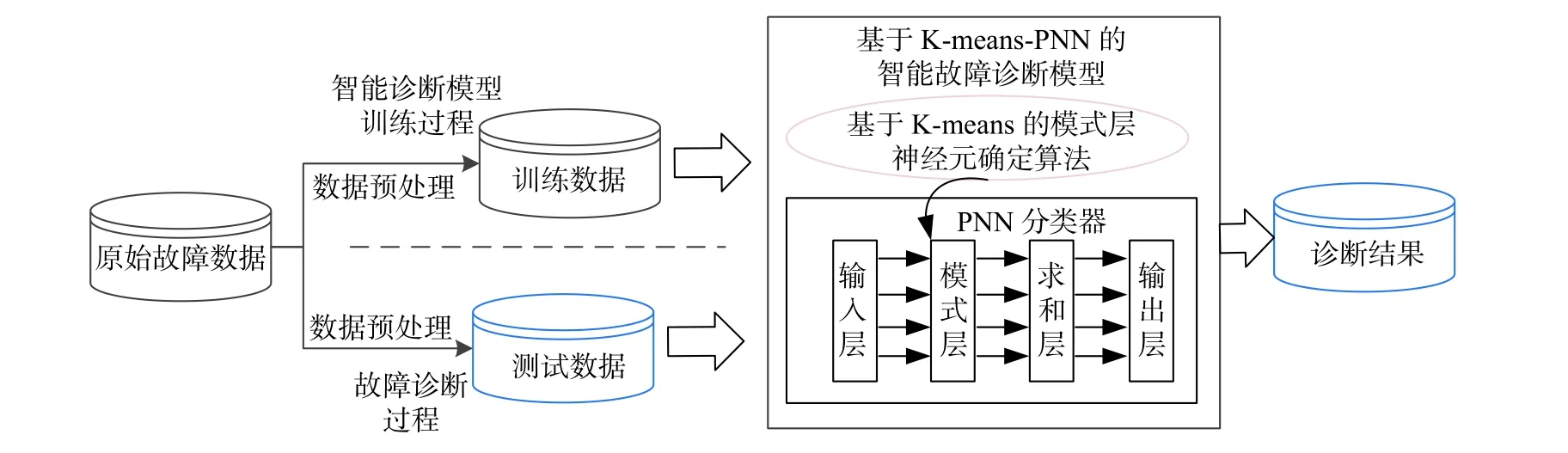
图2 诊断方法实施流程图

3.2 基K-means的模式层神经元优选算法

基于K-means的模式层神经元优选算法主要是通过对同一状态下的数据进行K-means聚类分析，根据聚类有效性指标确定聚类个数K，并寻找到聚类中心作为模式层神经元样本。具体流程如表2所示。

表2 模式层神经元优选流程

聚类有效性指标——CH指标，CH越小代表此时类自身越紧密，类与类之间越分散，即聚类结果更优，公式如下：

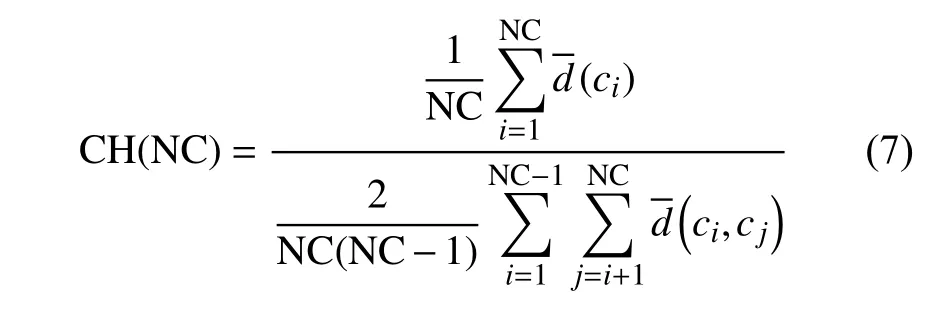
式中： N C——类的总数；

4 实验与分析

典型的有源滤波电路被用于验证本文方法的有效性，电路如图3所示，电路的输入电压为5 V，设有3个测试点，所以电阻和电容的容差设置为5%，仿真持续时间设定为10 ms，选取某一时间段内波形的最大电压值作为测试点的特征数据。电路的故障清单如表3所示，主要包括1个正常状态，6个故障状态。在每个状态下进行了500次的蒙特卡洛仿真分析，每种状态下获取了500个数据样本，7个状态，共3 500个样本，其中各个状态下的400个样本用于训练，100个用于验证。

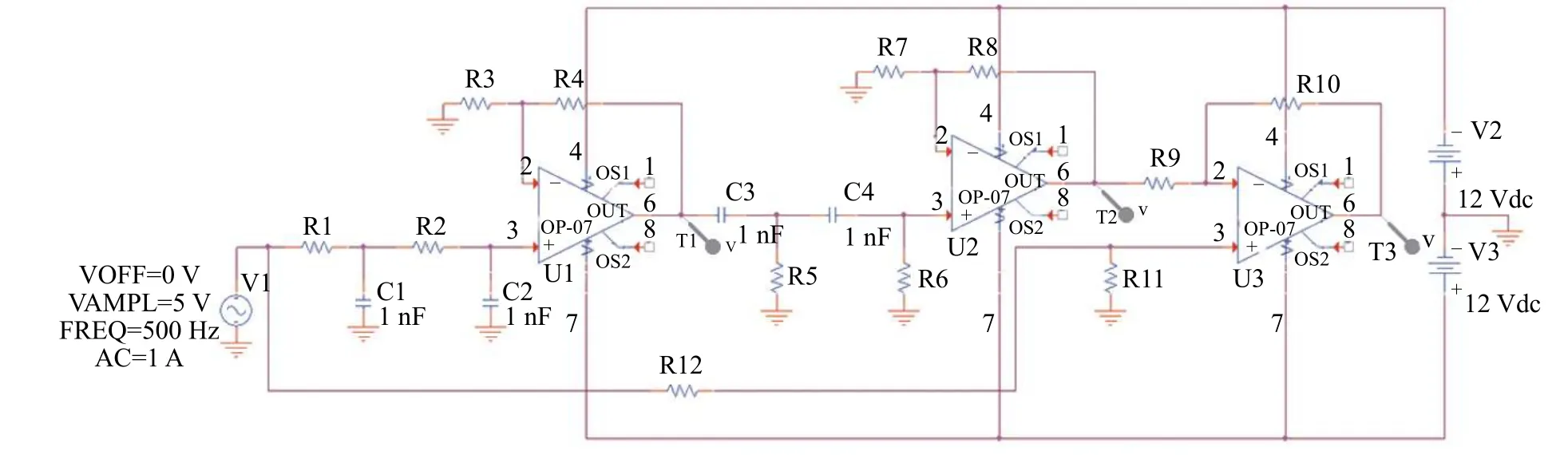
图3 有源滤波电路

表3 电路故障状态列表

基于K-means的模式层神经元优选算法对正常状态下的400个样本数据以K=1 ,···,100进行聚类分析，每选取一个K值，将通过式（7）进行一次聚类有效性指标的计算，最终得到100个聚类有效性指标值，得到的聚类有效性指标如图4所示，从图可知，当K值取1的时候聚类有效性指标最大，随着K值得增加，聚类有效性指标也逐渐变小，当K值取40的时候聚类有效性指标值趋于平缓，因此，本文选取最终的K值为40。通过K-means聚类分析可以得到40个聚类中心，这40个聚类中心将作为模式层神经元的训练样本。由于聚类中心不会是该训练数据集的离群点，因此，这种方式不仅大大减少了概率神经网络中模式层神经元的数量，还可以通过样本优选将离群点剔除。按照上述相同的操作，可以对其他6个故障状态进行模式层神经元样本优选,从而确定所有的模式层神经元样本集合。

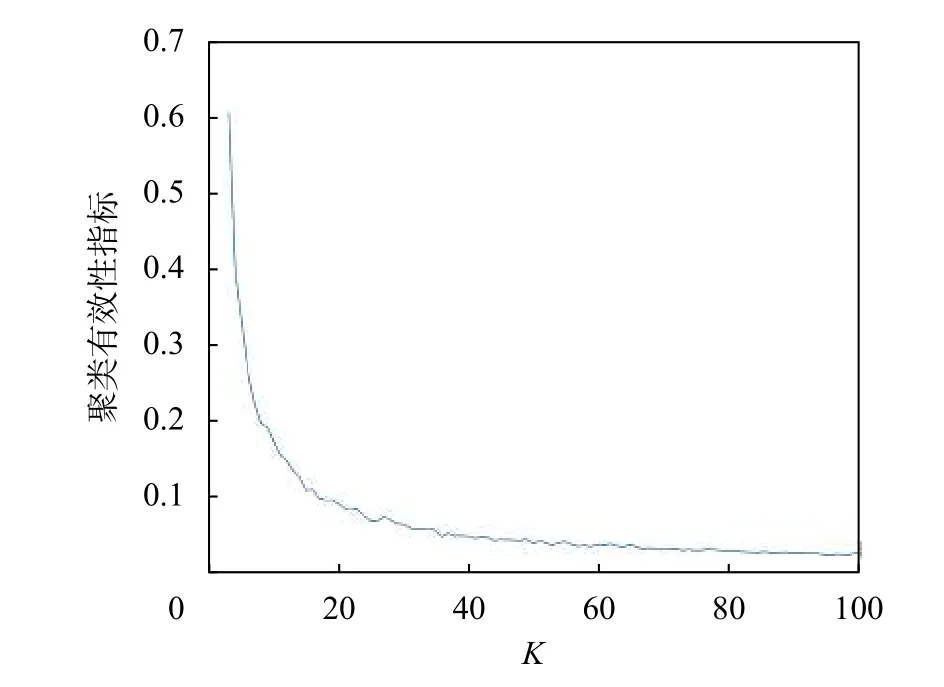
图4 聚类有效性指标

聚类中心的数目对建模效果有较大影响，聚类数目和故障诊断准确率之间的关系分析如图5所示。从图中可知，随着聚类数量的增加，故障诊断的准确率也在不断增加，当聚类数量达到40的时候故障诊断的准确率趋于稳定。

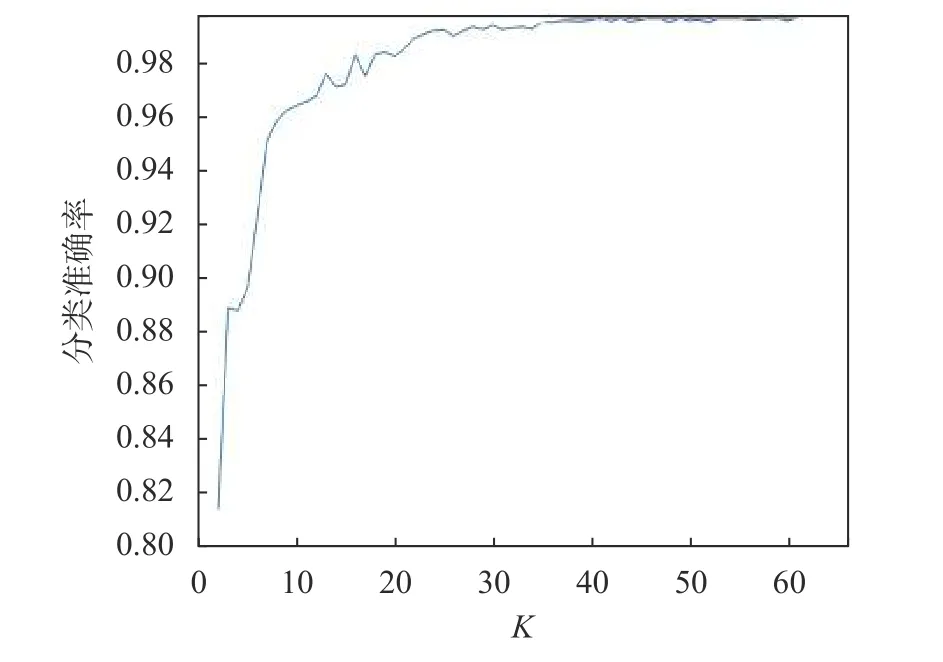
图5 聚类数目和故障诊断准确率关系

根据上一步得到的所有类别下模式层神经元训练样本，训练了概率神经网络模型，其中输入层神经元数量为3，模式层神经元数量为280，求和层神经元数量为7，输出层神经元数量为1。最后用700个验证数据输入模型，进行故障诊断，验证方法的有效性。主要从诊断模型规模、诊断准确性、故障诊断时间上对比本文方法与传统的PNN方法以及随机PNN方法。传统PNN方法采用所有的训练样本作为模式层神经元进行训练，即模式层神经元为2 800个；随机PNN是在训练样本集中随机抽取280个训练样本作为模式层神经元进行训练，因此它的模型规模大小与本文方法一样。

3种方法针对训练样本数据的故障诊断结果对比如表4所示，针对测试数据的故障诊断结果对比如表5所示。从表4中可看出，虽然传统PNN方法对于训练数据的故障诊断结果达到了100%，但是传统PNN的方法利用了所有的训练样本进行模型训练，需要2 800个模式层神经元，故障诊断时间需要27 s，并且从表5可知，虽然传统PNN对训练数据有较高的分类准确率，但模型泛化能力不足，易出现过拟合现象，导致对测试数据的分类准确率较低。

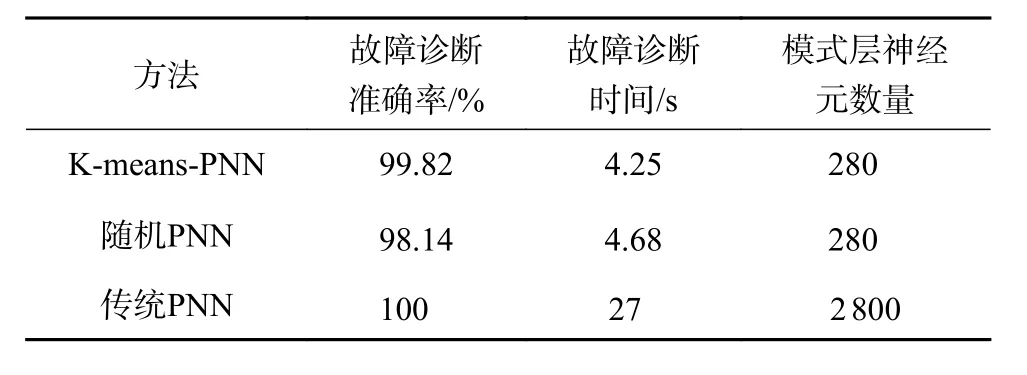
表4 对训练数据的诊断结果比较

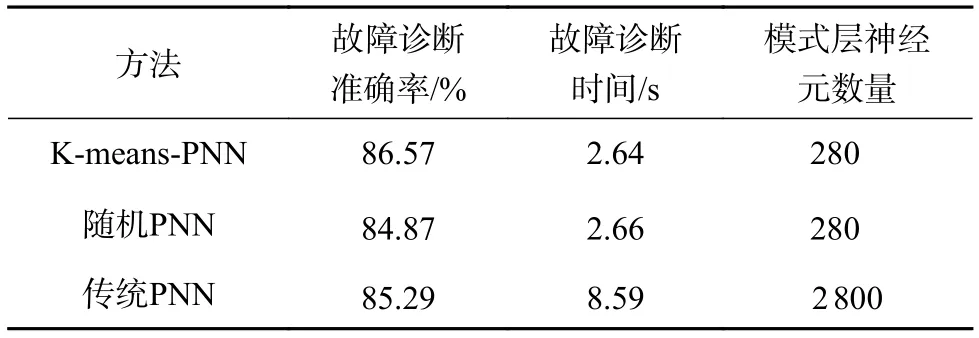
表5 对测试数据的诊断结果比较

随机PNN方法在故障诊断时间和模式层神经元数量上与K-means-PNN方法接近，但在对于训练数据的故障诊断准确性以及测试数据的故障诊断准确性上，K-means-PNN方法都具有明显优势。

传统PNN方法由于使用所有的训练样本作为模式层神经元，模式层神经元数量是K-means-PNN方法的10倍，这增加了模型的复杂性，加大了诊断过程的计算量，因此故障诊断的时间大大增加了，该方法的故障诊断时间是K-means-PNN方法的近3倍，并且，训练数据中很可能因为噪声、容差的影响存在一些离群点，这些离群数据会导致诊断准确性下降，从表5可看出，对于训练数据，传统方法比K-means-PNN方法在故障诊断准确性上低了近1个百分点。

随机PNN方法虽然通过随机抽取的方式大大减少了模式层神经元样本，节省了故障诊断时间，但各类样本中抽取多少个样本数据作为模式层神经元仍然是个问题，抽取的样本数量会影响故障诊断模型的性能，如果抽取的样本数量太多，虽然可以增加模型的稳定性，减轻离群点的影响，但同样会增加模型复杂性、增加故障诊断时间；抽取的样本数量太少，虽然可以降低诊断模型的复杂性、节省故障诊断时间，但模型的稳定性会降低，离群点对模型的影响会更大。此外，由于模式层神经元样本是通过随机抽取的，这个过程中存在很大的随机性，离群点数据有可能被选为模式层神经元样本，这会大大降低模型的故障诊断准确性。

而本文提出的K-means-PNN方法通过构建聚类有效性指标函数确定模式层神经元的数量，采用K-means聚类的方式，选取聚类中心作为模式层神经元，可以避免离群点对故障诊断准确性的影响，通过训练样本优选，使得训练样本大大减少，降低了模型的复杂程度以及计算量，因此所需要的故障诊断时间也大大降低。该方法可以实现较少的训练样本情况下达到较高的故障诊断准确性。

此外，本文方法与BP神经网络（BPNN）、KNearest Neighbor算法（KNN）、Random Forest算法（RF）在故障诊断准确率方面进行了比较，故障诊断结果对比如表6所示，本文提出的K-means-PNN方法均优于上述3种方法。

表6 与不同分类器算法结果比较

5 结束语

本文提出了基于K-means与概率神经网络相结合的模拟电路故障诊断方法，通过K-means聚类与聚类有效性指标的综合分析，给出了模式层神经元优选流程，筛选出合适的训练样本数据作为概率神经网络的模式层神经元参与训练，以较少的训练样本，实现了高故障准确性的故障诊断，减少了模型的复杂度，大大节省了故障诊断时间，通过与传统PNN方法、随机PNN方法、BP神经网络算法、KNN算法、以及RF算法的对比，说明了本文方法在故障诊断准确性以及故障诊断时间上的优越性能。