涡旋压缩机涡旋齿侧壁油膜承载力仿真分析

李洪福 胡兆稳 梅 亚 李 浩

(1.合肥工业大学机械工程学院 安徽合肥 230009；2.合肥安信瑞德精密制造有限公司 安徽合肥 230081)

涡旋压缩机作为第四代容积式压缩机，因高效、微振、低功耗、体积小等优点，被大量应用于家用冰箱、空调、电动汽车等工业产品之中。但涡旋压缩机内部摩擦副众多也是其缺点之一，特别是近年来，随着涡旋压缩机向高速、大功率、大压缩比方向发展，涡旋压缩机内部各摩擦副的润滑、磨损问题显得愈发突出。曹霞等人[1]分析了立式高压型涡旋压缩机主、副轴承，动涡盘轴承，动、静涡旋盘啮合齿间和齿顶端面的摩擦功，得出主、副轴承和动涡盘轴承上的摩擦功率相对较大的结论。LIU等[2]分析计算了涡旋压缩机主、副轴承，动涡盘轴承和动涡盘与机架间的推力轴承造成的摩擦损失，并对其进行了优化。AHN等[3]分析了动涡盘与机架间的推力轴承油膜特性在不同主轴回转角下的情况，得出倾覆系数对推力轴承油膜承载力起到关键作用的结论。AHN等[4]分析了高速涡旋压缩机动涡盘轴承最小余隙的影响因素。在良好润滑条件下，高速运转的动、静涡旋盘啮合齿侧壁间会形成一层流体动压润滑油膜[5]。作为涡旋压缩机的关键摩擦副之一，涡旋齿侧间的相对运动速度高，接触线长，容易产生润滑失效，甚至严重磨损，导致气体泄漏量增大，降低容积效率与使用寿命，但目前尚鲜有学者对其进行相关研究。

本文作者通过对涡旋齿的数学模型进行分析，求解出啮合点随偏心轴转角的变化规律，并借助现代流体动压润滑理论构建了涡旋齿侧壁间流体动压润滑油膜的理论模型；同时利用有限差分法求解油膜压力分布，分析了主轴转角、主轴转速、润滑油黏度、偏心率及涡旋体高度对润滑油膜承载力的影响。

1 涡旋压缩机的结构和工作原理

文中研究对象为某型号电动汽车空调用涡旋压缩机，其涡旋盘型线为圆的渐开线，动、静涡旋体等壁厚，且各自对称于壁厚中心面。如图1所示，其主要由动涡盘、静涡盘、柱销式防自转机构、径向柔性调节机构、偏心轴等部分构成。柱销式防自转机构安装在动涡盘背部，用于限制动涡盘的自转。

图1 涡旋压缩机的结构

在压缩过程中，静涡盘与机架固定不动，在偏心轴的驱动下，动涡盘将相对于静涡盘作圆周平移运动，这样在动、静涡盘的涡旋齿间便形成了数对位置和体积不断变化的月牙形容积腔，如图2所示。随着动涡盘的连续转动，月牙形容积腔不断向中心压缩，最终在静涡盘中心的排气孔处释放，完成气体压缩。

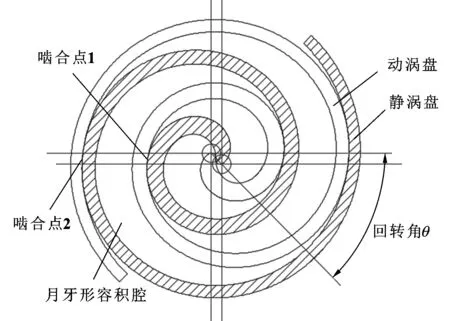
图2 动、静涡旋盘截面图

2 涡旋齿侧壁油膜模型的建立

2.1 啮合点处的曲率

设基圆半径为a的渐开线上有一任意点M，对应的渐开线展角为φ，由渐开线的性质易得点M的曲率半径R[6]为

(1)

当把动、静涡旋盘组合在一起形成压缩腔并假设主轴回转角为θ时，如图2所示，将形成数对啮合点，当回转角达到排气角θ*时，最内侧2个压缩腔相连通，开始排气，最靠近内侧的2个对称啮合点也将成对消失。因为对称啮合点处的动压润滑油膜同样具有对称性，因此只需分析一个啮合点处的油膜即可。以图中最靠近中心的啮合点1为例：当回转角0≤θ<θ*时，此刻的啮合点由动涡盘内壁面和静涡盘外壁面啮合而成，啮合点处对应的动、静涡盘壁面的渐开线展角分别为2.5π-α-θ和1.5π+α-θ[7]；随着θ越来越大，啮合点不断向中心靠拢，当回转角θ=θ*时，这对啮合点消失。当回转角θ*≤θ<2π时，原啮合点2运动成为最靠近中心的啮合点，对应的动、静涡盘壁面的渐开线展角分别为4.5π-α-θ和3.5π+α-θ。综上所述，由式(1)可得距离中心第k个啮合点处的动涡盘内壁面和静涡盘外壁面间的曲率半径与偏心轴回转角θ间的关系为

(2)

式中:Roi表示距离中心第k个啮合点处的动涡盘内壁面曲率半径;Rfo表示距离中心第k个啮合点处的静涡盘外壁面曲率半径。

2.2 油膜厚度方程

在实际情况下，动、静涡旋盘涡旋齿在啮合点处的间隙相比此处对应的曲率半径小得多，因此，可以用该啮合点处动、静涡旋齿的曲率圆来近似求解油膜厚度。结合图3，中心啮合点1处(k=1)的油膜厚度h可由式(2)得到：

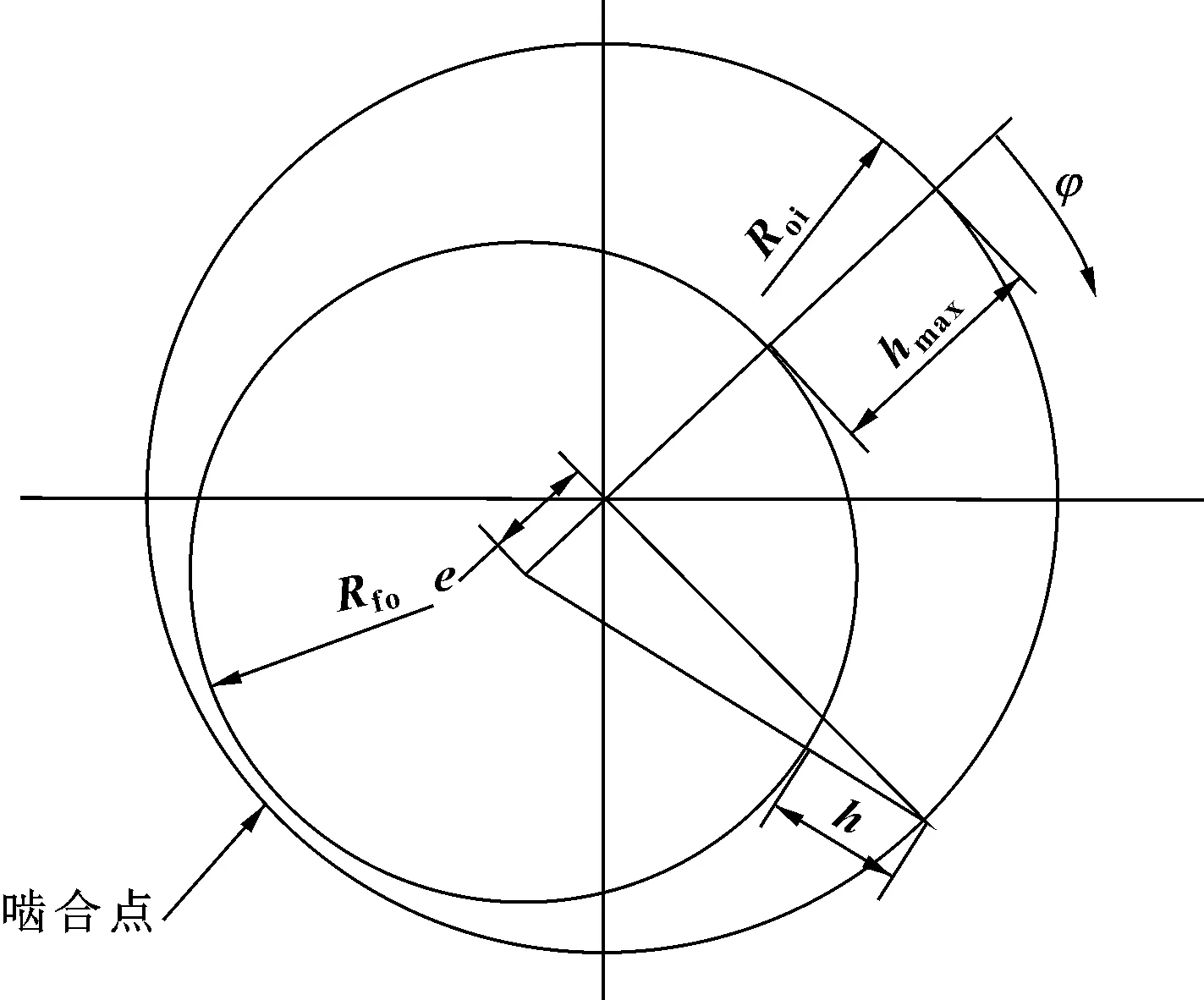
图3 油膜厚度

(3)

式中:e为偏心距;角坐标φ的参考原点在最大油膜厚度hmax处。

2.3 Reynolds方程

文中研究基于以下假定条件：

(1)润滑剂不可压缩，润滑剂黏度为常数；

(2)动、静涡旋盘间无径向和轴向窜动；

(3)动、静涡旋盘为刚性，不发生弹性变形；

(4)动、静涡旋盘间无相对偏斜。

涡旋齿侧壁间的流体动压润滑油膜压力分布可根据流体动压润滑理论，采用二维Reynolds方程求解[8]：

(4)

式中:h为油膜厚度;p为油膜压力;x为啮合点的切线方向;z为涡旋体轴线方向;U为啮合点处动涡旋盘的速度;μ为润滑油黏度。

需要指出的是，由于动涡旋盘相对于静涡旋盘作圆周平移运动，所以动涡旋盘上任意点的速度相等，即U=ωr。其中，ω为偏心主轴转速，r为动涡旋盘的回转半径。

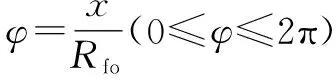
(5)

2.4 油膜承载力

定义切向油膜对动涡盘的承载力为Fx，径向油膜对动涡盘的承载力为Fy，其计算公式分别[10]为

(6)

承载力合力Ft为

(7)

如图2所示，该型号压缩机共有两对啮合点，设啮合点1处油膜承载力合力为Ft1，啮合点2处油膜承载力合力为Ft2，则总油膜承载力F为

F=2Ft1+2Ft2

(8)

3 求解过程

3.1 计算流程

利用有限差分算法求解Reynolds方程[11]，并采用雷诺边界条件[12]，可求得油膜压力分布。进一步对其进行数值积分即可求得油膜承载力[13]。在MATLAB中实现的程序流程图如图4所示。相对收敛准则为

图4 计算流程

(9)

式中：m为周向网格数；n为轴向网格数；K为迭代次数。

3.2 模型验证

为验证已建立的涡旋压缩机涡旋齿侧壁间油膜模型的正确性，利用该模型与径向滑动轴承动压润滑模型的相似性，在相同结构参数条件下，对两者进行比较。如图5所示，是在表1参数下计算得到的油膜量纲一化压力分布，其结果与文献[14]中的结果基本一致，验证了该模型的正确性。

图5 油膜压力分布

表1 验证模型参数

4 计算结果与分析

应用文中建立的涡旋压缩机涡旋齿侧壁间油膜流体动力润滑模型，对某型号电动汽车空调用涡旋压缩机进行分析计算。涡旋体主要参数见表2。

表2 涡旋体参数

4.1 油膜承载力与主轴转角的关系

由于啮合点处的动、静涡旋盘曲率半径随主轴转角时刻变化，导致油膜承载力也随主轴旋转而发生变化。如图6所示，是在主轴转速n=6 000 r/min，偏心率ε=0.98，涡旋体高度l=20 mm，润滑油黏度η=0.015 Pa·s条件下，最靠近中心的啮合点处润滑油膜承载力Ft1和总承载力F随主轴转角的关系。可以看出，在主轴转角小于排气角时，中心啮合点处的油膜承载力随主轴旋转而下降；在排气角θ*处，油膜承载力陡增，随后再次下降。究其原因，是因为主轴的旋转使啮合点向中心移动，在移动过程中Roi/Rfo逐渐变大，即进油口的楔形角变大，同时油膜承载区变小，致使油膜承载力变小；在主轴转角达到θ*时，最内侧2个啮合点消失，最外侧一对新啮合点形成，原外侧啮合点运动成为最靠近中心的啮合点，由此导致了图中油膜承载力的陡增。

图6 油膜承载力随主轴转角的变化

4.2 油膜承载力与主轴转速和润滑油黏度的关系

主轴转速对油膜承载力有一定影响[15]。如图7所示，是在偏心率ε=0.98，涡旋体高度l=20 mm，主轴回转角θ=1.51π时，中心啮合点处油膜承载力随主轴转速和润滑油黏度的变化曲线。可以看出，该啮合点处油膜承载力随主轴转速呈线性递增规律。这是因为，随着主轴转速的增加，啮合点进油口的进油量增大，使油膜高压区和低压区之间产生更大的压力差，从而提高了油膜承载力。同时，油膜承载力又受到润滑油黏度的影响，在相同主轴转速下，油膜承载力随润滑油黏度增大而增大，并且主轴转速越高，增大润滑油黏度对提高油膜承载力的作用越明显。所以在低转速下，可以选用黏度稍高的润滑油，而在高转速下，可以选用黏度稍低的润滑油，以保证良好的润滑效果。

图7 油膜承载力随主轴转速和润滑油黏度的变化

4.3 油膜承载力和最小油膜厚度与偏心率的关系

作用在油膜上的外载荷由动涡盘的残余离心力，即径向密封力提供[16]，密封力越大，偏心率越大。图8所示是在主轴转速n=6 000 r/min，主轴回转角θ=1.51π，润滑油黏度η=0.015 Pa·s，涡旋体高度l=20 mm条件下，中心啮合点处润滑油膜承载力和最小油膜厚度hmin随偏心率的变化关系。可知，油膜承载力随偏心率的增大而增大，最小油膜厚度随偏心率的增大而减小。偏心率接近于1时，油膜承载力趋于无穷大，最小油膜厚度趋于0。所以，为保证良好的润滑，偏心率不宜过大，以防止最小油膜厚度太小，导致油膜破裂；另一方面，为保证良好的密封效果，偏心率不宜过小，以防止齿侧间隙太大，导致气体泄漏量增大。

图8 油膜承载力和最小油膜厚度随偏心率的变化

4.4 油膜承载力与涡旋体高度的关系

涡旋体高度也是影响油膜承载力的关键因素之一。如图9所示是在主轴转速n=6 000 r/min，偏心率ε=0.98，主轴回转角θ=1.51π，润滑油黏度η=0.015 Pa·s条件下，中心啮合点处润滑油膜承载力和涡旋体高度的关系。可以看出，涡旋体高度从20 mm增长到40 mm过程中，该啮合点处的油膜承载力逐渐变大。由式(5)可以看到，润滑油膜压力是l的函数，增大涡旋体高度l可以提高油膜承载力，但其提高的幅度逐渐减小。

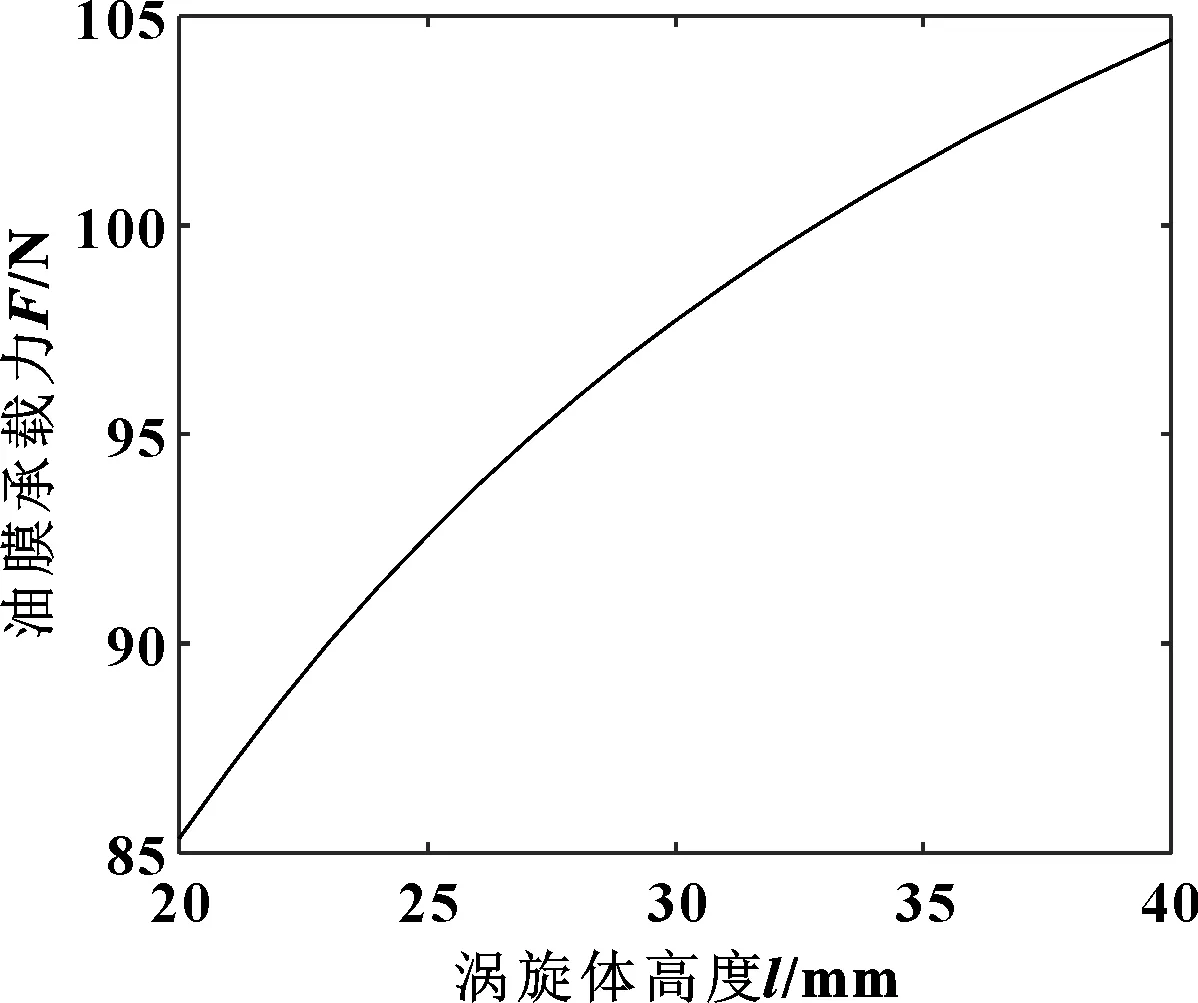
图9 油膜承载力随涡旋体高度的变化

5 结论

(1)在良好润滑条件下，涡旋体侧壁间油膜承载力随主轴转角先减小，达到排气角θ*时会陡增，随后再次减小。因此，在旋转角接近排气角处油膜承载力最小，最容易产生润滑失效。

(2)在一定范围内，涡旋体侧壁间油膜承载力随主轴转速的增加而增大，随润滑油黏度的增加而增大，并且，主轴转速越高，润滑油黏度对油膜承载力的影响越大。因此，为使油膜具备一定的承载力，在低转速时，适合选用黏度稍大的润滑油，在高转速时，适合选用黏度稍小的润滑油。

(3)润滑油膜的承载力随偏心率的增大而增大，但过大的偏心率会导致最小油膜厚度减小，使油膜出现破裂，从而带来摩擦、磨损问题；过小的偏心率又会导致齿侧间隙过大，压缩气体泄漏量增大的问题。所以，在设计过程中应合理设计密封力的大小，使偏心率处在合理范围内。

(4)适当增加涡旋体高度有利于提高涡旋体侧壁间油膜的承载能力，但也应注意到由此带来的散热问题。