数学基础课里的中国剩余定理和Lagrange插值公式
刘合国,徐行忠,廖军
(湖北大学数学与统计学学院, 湖北 武汉 430062)
中国剩余定理在数学里起着重要的作用,是中国先贤智慧的结晶.该定理从数系的基本运算律出发,用最典型的“线性”方法解决问题,这种思想是极其深刻的.这些年来,我们在从事高等代数、初等数论、近世代数、代数学等课程的教学过程中,积累了对这个定理的认识,它们对理解这个定理是有作用的.现不揣浅陋,撰写成文,望同好者批评指正.
本文中采用的术语和符号都是标准的,按照文献[1-3].
1 四首歌诀
《孙子算经》是中国古代的一部数学名著,成书于公元三世纪至五世纪左右,其卷下之26题,即是历史上有名的“物不知数”:
今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
《孙子算经》不仅给出了正确答案,而且给出了完美的解法:
答曰:二十三.
术曰:三三数之剩二,置一百四十;五五数之剩三,置六十三;七七数之剩二,置三十.并之,得二百三十三,以二百一十减之,即得.
凡三三数之剩一,则置七十;五五数之剩一,则置二十一;七七数之剩一,则置十五.一百六以上,以一百五减之,即得.
用现代语言重现这个解法,即同余方程组
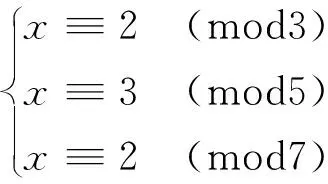
的答案为: 140+63+30=233,233-210=23.
一般地,求解同余方程组

的几个关键数字是 70,21,15和105,答案为r:
70a+21b+15c=105q+r,1≤r≤105.
这个解法是非常奇特的!初看起来,它是迂回的,不是单刀直入的,但它抓住了问题的本质,找到了最关键的节点,通过线性组合得到答案.这是绝顶的智慧!南宋淳熙十五年(1188),大型类书《锦绣万花谷》问世,其前集卷三十八记载了一首“易数诗”:
三人同行七十稀,五郎念一镇相随,
七哥记取常十五,此是易数大希夷.
这里“念”是“廿”的大写,代表二十,诗里明白地点出了三个最关键的数字:70,21,15.面对虚寂玄妙的解答,古人发出了“易数希夷”的感叹.
在中国古代数学家里,秦九韶对中国剩余定理做出了决定性的贡献.秦九韶(1208—1261),字道古,生于普州安岳(今四川省安岳县),在南宋淳祐七年(1247)完成了不朽著作《数书九章》,它是中国古代最重要的数学著作之一.科学史家George Sarton在所著《Introduction to the history of science》之卷II.2里高度评价秦九韶:
One of the greatest mathematicians of his race,of his time,and indeed of all times.
在《数书九章》里,秦九韶创造性地发明了大衍求一术,即给出了解同余方程ax≡1(modm)的一般算法,这是求解中国剩余定理的决定性步骤.
有宋一代,华夏文明昌盛,道学繁荣.秦九韶对他的数学成就是非常自豪的,《数书九章》序说:
(数)大则可以通神明,顺性命;小则可以经世务,类万物.要其归,则数与道非二本也.
秦九韶将数学提升到“道”的高度.清代扬州学派的代表人物之一,“扬州通儒”焦循(1763—1820)在《天元一释》卷下高度评价秦九韶的历史功绩:
大衍之术,即《孙子算经》三三五五七七之术也.此术《九章》所无,而见于《孙子》.今则归入孺子,或以为戏.《孙子》虽详其术,而秦氏则阐其微而畅发之.其三三置七十,即大衍求一术也.
中国剩余定理玄妙高远, 不断被编成歌诀进入小说笔记, 这个现象是十分罕见的.
周密(1232—1298),字公瑾,生于杭州,工诗词,擅书画,是南宋笔记大家,著述甚丰,所著《志雅堂杂钞》卷九之“阴阳算术”记载了一首解答“物不知数”的歌诀:
三岁孩儿七十稀, 五留廿一事尤奇,
七度上元重相会, 寒食清明便可知.
前两句蕴含了两个数字:70和21.上元节就是元宵节,借指正月十五,这样第三句蕴含了数字“15”.第四句蕴含了数字“105”,需要做点说明:在中国古代的很长时间里,把冬至当作新年的开始,冬至距寒食清明节多在105天.这样解“物不知数”的关键数字:70,21,15和105都在歌诀里出现了.
褚人获(1635—1682),字稼轩,江苏长州人.未中试,多才多艺,著有《隋唐演义》,《坚瓠集》等.其《坚瓠集》戊集卷一之“隔壁笑”记载了一首歌诀:
三人逢零七十稀,五马沿盘廿一奇(一作五人折桂廿一枝),
七星约在元宵里,一百零五定为除.
显然,这首歌诀同样写下了解“物不知数”的四个关键数字:70,21,15和105.
程大位(1533—1606),字汝思,安徽休宁人.他在经商过程中,积累了丰富的数学问题及其解法,编撰了《直指算法统宗》,强调指出数学在国计民生中的重要性,其《书直指算法统宗后》写道:
数居六艺之一,其来尚矣,盖自虙戏宰世,龙马负图,而数肇端.轩后纪历,隶首作算,而法始衍.故圣人继天立极,所以齐度量而立民信者,不外黄钟九寸之管,所以定四时而成岁功者,不外周天三百六十五度之数.以至远而天地之高广,近而山川之浩衍,大而朝廷军国之需,小而民生日用之费,皆莫能外.数讵不重己哉?
程大位在书里把不少问题的解法用歌诀的形式呈现出来.特别地,他在卷五里将“物不知总”的解法写成了通俗易懂、广为传颂的“孙子歌”:
三人同行七十稀,五树梅花廿一枝,
七子团圆正半月,除百零五便得知.
“物不知数”及其解法的影响超出了数学之外,例如金庸在他的成名之作《射雕英雄传》里,就引述了“物不知数”和程大位的歌诀,用来加强其行文的份量.当然,这属于“误引”,因《射雕英雄传》讲述的是南宋故事,那时程大位的歌诀还未问世.中国剩余定理对中国文化的影响于此也可见一斑.
2 歌诀的意义
在这节我们要研究为什么70,21,15和105就是求解“物不知数”的关键.105=3×5×7,105的来历是一目了然的,容易看到
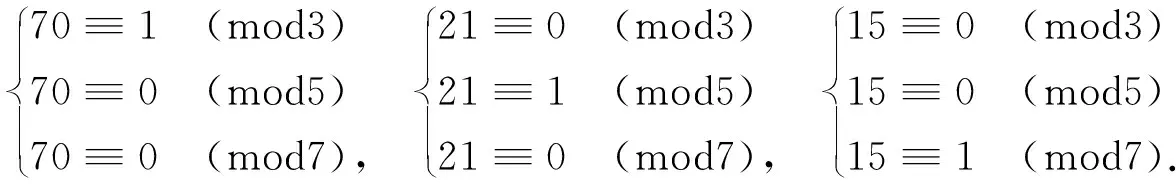
粗略地说,70,21,15就是求解同余方程组

(1)
的“基底”,a,b,c只是解的“坐标”.方程组 (1)的解为
x≡a·70+b·21+c·15(mod105).
按照中国古代传统,取x为最小正整数当作方程组(1)的解.
为了理解上面“基底”的准确意义,我们引进一个概念.
设R是含幺交换环,RM是R上的模.如果X是M的非零元组成的子集,满足
1)M的任意元m可表示为m=r1x1+r2x2+…+ruxu,ri∈R,xi∈X,即M=∑x∈XRx.
2)若s1y1+s2y2+…+svyv=0,其中si∈R,yi∈X, 则s1y1=s2y2=…=svyv=0.
那么我们称X是M的一组基底.



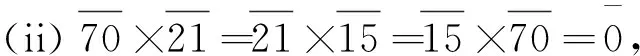

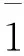
顺便提一下,含幺环里单位元的正交幂等元之分解是研究环结构的重要工具.
例1解方程x3-3x+5≡0 (mod105).
解:方程化为
化简(2a)式,由Fermat小定理,x3≡x(mod3),得
x≡1(mod3)
(3)
化简(2b)式,x(x2-3)≡0(mod5),因5x2-3, 故
x≡0(mod5)
(4)
化简(2c)式,由Fermat小定理,x6≡1(mod7),故x3≡±1(mod7),代入(2c)式,得3x≡5±1(mod7),所以
x≡2(mod7)或x≡6(mod7)
(5)
运用歌诀解得x≡100(mod105)或x≡55(mod105).
3 中国剩余定理
理解了前一节里70,21,15在求解“物不知数”的意义,我们就可以自然地推出一般形式的中国剩余定理,其中的关键一步是秦九韶的“大衍求一术”.
定理3.1(中国剩余定理) 设m1,m2,…,mn是两两互素的正整数,对任意整数a1,a2,…,an,下列方程组
在模m1m2…mn下有唯一解.
定理3.1的证明对任意的1≤i≤n, 设xi满足同余方程组
xi≡δij(modmj),1≤j≤n.
其中δij是Kronecker符号,xi≡1(modmi)等价于xi+uimi=1;对所有的j≠i,xi≡0(modmj)等价于xi=vi∏j≠imj.即有
因(mi,∏j≠imj)=1,据大衍求一术,可得ui,vi,进而得到xi.
记x=a1x1+a2x2+…+anxn,容易验证x即是解.
下证唯一性.设a,b是方程组的两个解,则有
则a≡b(modmi)对任意的1≤i≤n成立,于是a≡b(modm1m2…mn).
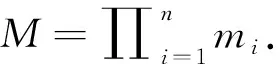
uimi+viMi=1.
取xi=viMi.将上述前n-1个式子相乘得到
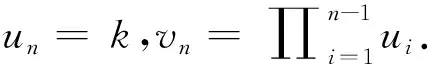
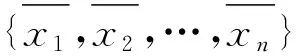
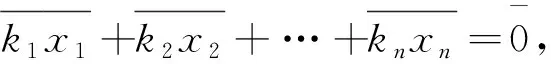
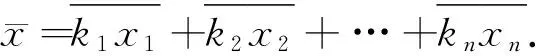
另一方面,容易验证如下的事实.
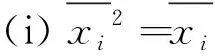
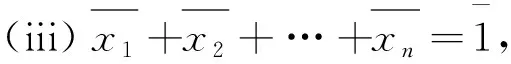
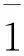
中国剩余定理是解决存在性问题的有力工具.
例2证明对任意正整数n,均存在n个连续整数,它们都有一个平方因子.
证明选取n个互异素数p1,p2,…,pn,考虑下面的同余方程组
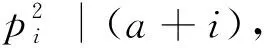
例3证明对任意正整数n,存在整数a和b,使对任意的1≤r,s≤n,都有(a+r,b+s)>1.
证明选取n2个互异素数pij,1≤i,j≤n.设a是同余方程组
的解,b是同余方程组
的解.对任意的1≤r,s≤n,有prs∣(a+r,b+s),从而(a+r,b+s)>1.
4 单刀直入的解法
在上一节求解线性同余方程组时,我们采用的方法是间接地找到所需的“基底”,再通过线性组合得到问题的答案,这与我们之前求解线性方程组的思路具有很大不同.接下来,我们借用解线性方程组的理念来处理中国剩余定理的求解问题,其出发点是下面两条:
(i) 设k,m是正整数,a,b是整数,则
a≡b(modm)⟺m∣(a-b)
⟺km∣(ka-kb)
⟺ka≡kb(modkm)
(ii) 中国剩余定理.
下面设m1,m2,…,mn是两两互素的正整数,对任意整数a1,a2,…,an,求解同余方程组
(6)
为了进行线性运算,我们需要把模统一化,记M=m1m2…mn,Mi=M/mi.则上面的方程组(6)式等价于下面的方程组(7)式.
(7)
因(M1,M2,…,Mn)=1,故存在整数k1,k2,…,kn, 使k1M1+k2M2+…+knMn=1.于是x≡k1M1a1+k2M2a2+…+knMnan(modM).根据中国剩余定理里解的唯一性,x即为所求.
上面的步骤可以用两句话来概括.
(iii) 统一模,即把方程组(6)式化为方程组(7)式.
(iv) 凑“1”,即由方程组(7)里x的系数M1,M2,…,Mn经过整数线性组合凑出“1”即可.
下面举例说明.
例4(韩信点兵) 相传刘邦拜韩信为大将后,某天来到韩信的练兵场,见有约二千名士兵正在操练.期间韩信告诉刘邦,他并不知道练兵场上到底有多少士兵,但如果命令士兵们先后以七人一组,十一人一组,十三人一组集结成小组,并把每次余下不能组成七人(或十一人,或十三人)的人数报给他,他就可以知道士兵的准确人数.刘邦很惊讶,就按照韩信的要求做了一番操作,报给韩信三个数字:3,4,8.韩信很快就告诉刘邦,士兵数目是1 984.刘邦验证答案后,非常信服,确信韩信具有非凡的才能.
用数学语言翻译这个故事,即是求解

(8)
其中x在2 000左右.如果这个故事是真实的,那么在刘邦到来之前韩信肯定知道几个关键的数字:715, 364,924和7×11×13=1 001,韩信根据报给他的3个数:3,4,8,即可进行计算:
3×715+4×364+8×924=10 993,10 993-9×1 001=1 984,
1984就是士兵数目. 现在我们用本节的方法再来求解一次.
解: 同余方程组(8)等价于
(9b)-(9c)得
14x≡-252(mod1 001)
(10)
(9a)-(10)×10得
3x≡429+2 520≡2 949≡-54(mod1 001)
(11)
(9b)-(11)×30得
x≡364+54×30=1 984(mod1 001).
故操练的士兵数为1984.
我们可以把本节的方法推广到一般情形.
定理4.1设m1,m2,…,mn都是正整数,则同余方程组
有解的充要条件是对1≤i,j≤n,均有(mi,mj)∣(bi-bj).
当方程组有解时,记M=[m1,m2,…,mn],Mi=M/mi,则存在整数k1,k2,…,kn使得k1M1+k2M2+…+knMn=1,方程组的解为
x≡k1M1b1+k2M2b2+…+knMnbn(modM).
例5解同余方程组

解. 容易验证(mi,mj)∣(bi-bj), 因此方程组有解.由于[6,9,15]=90, 原方程组等价于

将第二个方程加上第三个方程减去第一个方程得到x≡67(mod90).
5 从中国剩余定理到Lagrange插值公式
设F是一个域,F上的多项式环F[x]和整数环Z是最常见的两个Euclid环.我们可以把前面的中国剩余定理推广到F[x]. 为方便计,先引进一个符号.
设m(x)是F[x]的非常数多项式,f(x),g(x)∈F[x],若m(x)整除f(x)-g(x), 则记为f(x)≡g(x)(modm(x)).这与Z上的同余符号具有类似的性质:
设f1(x)≡g1(x)(modm(x)),f2(x)≡g2(x)(modm(x)),k(x)∈F[x],则k(x)f1(x)+f2(x)≡k(x)g1(x)+g2(x)(modm(x)).
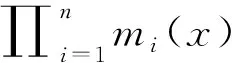
f(x)≡ri(x)(modmi(x)),1≤i≤n.
定理5.1的证明完全类似中国剩余定理的证明过程求f1(x),f2(x),…,fn(x).对任意的1≤i≤n,由于(mi(x),∏j≠imj(x))=1,则存在多项式ui(x),vi(x),使得ui(x)mi(x)+vi(x)∏j≠imj(x)=1.取fi(x)=vi(x)∏j≠imj(x).则fi(x)满足
fi(x)≡δij(modmj(x)),1≤j≤n.
记
g(x)=r1(x)f1(x)+r2(x)f2(x)+…+rn(x)fn(x)
=q(x)m1(x)m2(x)…mn(x)+r(x).
则r(x)即为所求方程组的解.
下证解的唯一性.设a(x),b(x)都是满足定理中方程组的解, 即
a(x)≡ri(x)(modmi(x)),1≤i≤n,
b(x)≡ri(x)(modmi(x)),1≤i≤n.

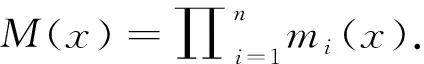
ui(x)mi(x)+vi(x)Mi(x)=1.
将上述n-1个式子相乘得到
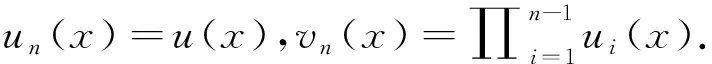

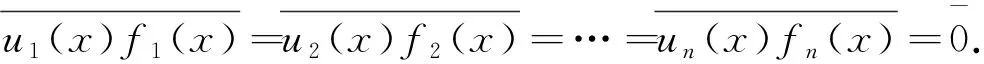
对任意g(x)∈F[x],g(x)=u1(x)f1(x)+u2(x)f2(x)+…+un(x)fn(x).于是
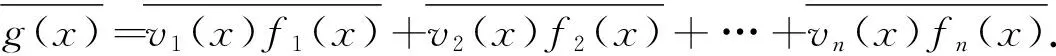
另一方面,在R上,我们容易验证下面的关系式:
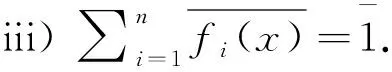
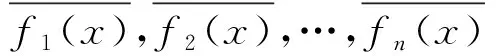
接下来我们考虑定理的最极端情况.设a1,a2,…,an是F上的n个两两互异的元素, 此时m1(x)=x-a1,m2(x)=x-a2,…,mn(x)=x-an是F[x]的两两互素的多项式.根据上述定理,对F上的任意n个元素b1,b2,…,bn, 存在唯一的次数小于n的多项式f(x), 使得对每个1≤i≤n, 有
f(x)≡bi(modx-ai),
即存在qi(x)∈F[x], 使f(x)=qi(x)(x-ai)+bi,这等价于f(ai)=bi,这样我们就得到了
定理5.2(Lagrange插值定理) 设a1,a2,…,an是F的n个两两互异的元素,则对F的任意n个元素b1,b2,…,bn,存在唯一次数 遵循中国剩余定理的思路,我们能够程序化地求出L(x). 对每个1≤i≤n, 求次数小于n的多项式Li(x), 使 Li(aj)=δij,1≤j≤n. 容易看出 这样L(x)=b1L1(x)+b2L2(x)+…+bnLn(x). L1(x),L2(x),…,Ln(x)是域F上的次数小于n的多项式构成的n维线性空间F[x]n的一组基底.事实上,L1(x),L2(x),…,Ln(x)线性无关.若k1L1(x)+k2L2(x)+…+knLn(x)=0,ki∈F,分别以x=a1,a2,…,an代入,则得k1=k2=…=kn=0. 又dimFF[x]n=n. 因此L1(x),L2(x),…,Ln(x)是线性空间F[x]n的一组基底. (iii)L1(x)+L2(x)+…+Ln(x)=1. 上节从中国剩余定理出发,导出Lagrange插值公式, 这个过程也是迂回的.由于本研究主要是从线性方法入手,下面给出Lagrange插值公式的另外两个线性代数证明. 证法一对F上的n个两两互异的元素a1,a2,…,an,以及F上的任意n个元素b1,b2,…,bn. 关于未知数x0,x1,…,xn-1的线性方程组 的系数行列式是a1,a2,…,an的Vandermonde行列式,它显然不等于0,故该线性方程组有且仅有一组解(x0,x1,…,xn-1),于是多项式L(x)=x0+x1x+x2x2+…+xn-1xn-1即为所求. 下面我们来求出这个多项式的显式表达.方程组的系数行列式为 根据Cramer法则, 其中Δk,i+1是Δ的第k行第i+1列元素的代数余子式,于是 L(x)=x0+x1x+x2x2+…+xn-1xn-1 证法二考虑下面的函数方程 则L(x)为所求的多项式当且仅当L(x)满足上述方程.事实上,按第一行展开左边的行列式,即知L(x)是F上次数小于n的多项式.当L(x)满足上述方程时,对每个1≤i≤n,有 则有 必须L(ai)-bi=0,即L(ai)=bi. 再按最后一列展开函数方程中的行列式,化简得到 在处理多项式的存在性问题时,中国剩余定理和Lagrange插值公式是两个合适的工具. 例6证明对任意的n阶复矩阵A, 存在多项式s(λ),n(λ),使得A=s(A)+n(A), 并且s(A)是可对角化矩阵,n(A)是幂零矩阵. 证明设A的特征值为λ1,λ2,…,λr,A的极小多项式为 设Ui为λi的根子空间,即 Ui={α∈Cn∣(A-λiE)miα=0}, 根据中国剩余定理,存在多项式s(λ),使得 我们断言s(A)是可对角化矩阵,A-s(A)是幂零矩阵.事实上,对每个1≤i≤r,从s(λ)≡λi(mod(λ-λi)mi),知存在fi(λ),使得s(λ)=λi+fi(λ)(λ-λi)mi.则有s(A)=λiE+fi(A)(A-λiE)mi.因此s(A)纯量地作用在Ui上,即有s(A)αij=λiαij,1≤j≤ni.于是s(A)有n个线性无关的特征向量,从而是可以对角化的. 例7设n阶矩阵A有n个互异的特征值,AB=BA. 证明B=f(A),对某个多项式f(x)∈F[x]成立. 证明由于n阶矩阵A有n个互异的特征值,则存在n阶可逆矩阵P,使得 由条件有AB=BA,故P-1APP-1BP=P-1BPP-1AP.注意到对i≠j,我们有λi≠λj,则可得P-1BP为对角矩阵.设 则由Lagrange插值公式,存在唯一次数小于n的多项式f(x), 使得f(λi)=μi,对所有的1≤i≤n成立. 因此P-1BP=f(P-1AP),从而得B=f(A). 前面涉及的中国剩余定理及其证明对一般的含幺环也是成立的,我们从文献[3]中摘录下面的两个定理,略去它们的证明. 定理8.1(中国剩余定理) 设含幺环R的理想I1,I2,…,In两两互素,则对R的任意元素a1,a2,…,an, 在模I1∩I2∩…∩In下有唯一解. 定理8.2设含幺环R的理想I1,I2,…,In两两互素,则有环同构 R/I1∩I2∩…∩In≅R/I1⊕R/I2…⊕R/In. 曾有专家认为,下面的群论结果也属于中国剩余定理. 设G是一个群,M和N都是G的正规子群,G=MN, 则 G/M∩N≅G/M×G/N. 我们是不能认同这个观点的.中国剩余定理是非常自然的插值工具,是数系运算之基本法则的绝佳体现,是线性方法的深刻应用.除了在形式上与定理8.2的最简单情况相似外,这个群论结果与中国剩余定理的内涵是没有什么关联的.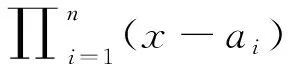
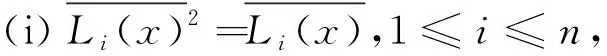
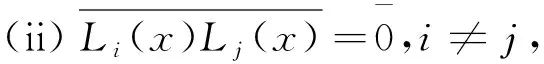
6 另两种线性代数推导
7 应用
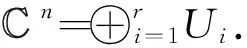
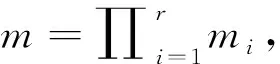
8 一般性结论

