基于模拟退火的自适应正余弦算法
张 娜,贺兴时
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
在科学技术飞速发展推动下,生产实践中面临的最优化问题的复杂度成倍增长。在探寻优化问题求解的过程中,大量群体智能算法[1-3]得以发展并广泛应用于科学研究和工程应用等领域。
正弦余弦算法(SCA)[4]是2016年澳大利亚学者Seyedali 和Mirjalili提出的一种新型智能算法。该算法将迭代过程归纳为全局搜索和局部开发2个过程。针对2个具体的过程加入不同的扰动,通过重复迭代找寻最优解。该算法参数少、结构简单、易于实现,因而得以广泛发展和应用。目前,SCA已经被用于资源配置[5]、调度问题[6]、电力系统优化[7]等组合优化问题。
正余弦算法(SCA)自身也存在缺点,如局部搜索能力差、迭代后期收敛过慢、易陷入局部最优等。对此,诸多学者从简化算法、调整参数、融合其他算法等方面提出了不同的改进策略。曲良东等为简化算法,将算法调整为正弦算法(SA),虽然降低了算法复杂度但牺牲了部分精度[8];刘勇等提出转换参数非线性递减的正弦余弦算法(PSCA),在一定程度上提高了计算精度和收敛速度[9];徐松金等在算法中引入惯性权重和反向学习策略,提出一种改进的正余弦算法(ISCA),提升了算法性能,特别是提高了高维函数求解的精度,但算法在迭代后期易陷入局部最优[10];王蕾等将正余弦算法改进后嵌入花粉算法,利用正弦和余弦对花粉个体进行优化,提出一种融合正弦余弦算法的花授粉算法,提升了算法寻优精度[11];韩斐斐等将正弦余弦操引入蝙蝠算法,避免算法陷入局部最优[12]。可见,改进的算法要么存在局部开发范围过小而导致算法陷入局部最优,要么存在全局搜索范围过大而导致算法寻优精度低的问题。本文针对正余弦算法的不足,自适应调整参数r1,在更新公式中引入对数递减的惯性权重,同时嵌入模拟退火机制,在增强局部探索能力,平衡局部与全局2个过程的同时,使算法在迭代后期能跳出局部最优。
1 标准正余弦算法
正余弦算法(SCA)是利用正弦、余弦函数的周期波动性构造迭代方程更新新解,并不断向最优解逼近。首先随机产生初始解并获取当前最优解位置,然后根据式(1)进行更新:
(1)
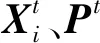
SCA算法伪代码如下:
b) 初始化各参数N、M, 令t=0,a=2。

d) Whilet≤M
fori=1:N
forj=1:d
计算r1,随机产生r2,r3,r4
ifr4<0.5
根据式(1)正弦部分更新位置
else
根据式(1)余弦部分更新位置
end if
end for
end for
t=t+1
end While
2 改进正余弦算法
2.1 自适应调整参数
标准正余弦算法中采用线性递减的参数r1,不利于平衡全局搜索和局部开发2个线性过程。为提高算法性能,文献[9]提出了转化参数抛物线递减和对数递减2种参数调整策略,并通过实验证明了转换参数指数递减的策略具有更高的寻优精度,如式(2)所示:
(2)
式中:控制参数a=2。但这种参数调整方式未考虑粒子自身状态,对于高维复杂函数求解存在局限性。考虑到进化过程各个粒子间的进化能力存在差异,本文提出将参数r1转为自适应参数,根据进化中每个粒子自适应值的状态,动态的调整参数r1,如式(3)所示:
(r1max-r1min)]
(3)
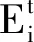
(4)

2.2 对数递减惯性权重
智能算法在进化前期需要很强的随机震荡,以获取全局最优; 进化后期则需提高局部开发能力。为此,SHI[13]提出一种惯性权重线性递减的粒子群算法(PSO)。为平衡算法全局探索和局部开发能力,参考粒子群算法,在位置更新中引入对数递减的惯性权重,表示粒子保持原来位置的惯性。为简化论述过程,将在简化正弦算法的基础上进行改进。因此,个体位置更新公式调整为式(5),惯性权重为式(6):
(5)
(6)


图 1 权重变化曲线图Fig.1 Weight change curve
2.3 基于模拟退火的正余弦算法
模拟退火算法(SA)是1953年N.Metropolis等基于固体退火原理提出的一种启发式算法[14]。该算法的核心是采用重要性采样方法,也称为Metropolis准则,以一定概率接受劣解,使算法能依概率跳出局部最优。因此,算法具有良好的全局寻优能力,将其与其他优化算法结合[15-16]可以提高改进算法性能。本文在正余弦算法中引入模拟退火的机制,称之为SASCA算法,以增强算法跳出局部最优的能力。
在SASCA算法中,每次迭代时对最优位置添加高斯扰动,以避免算法在迭代后期陷入局部最优。
Xt+1=Xt+αε
(7)
式中:Xt=(Xij)N×d;ε为N×d阶随机矩阵,矩阵中每个元素εij~N(0,1)。为避免波动范围过大,设置扰动因子α。经过测试,本文将α设置为0.01。
在SASCA算法中引入Metropolis 准则,对当前最优解添加高斯扰动得到全局最优的替代值,并根据Metropolis准则以一定概率接受扰动后的新解。基本迭代过程为:
a) 随机产生初始种群,设置初始参数种群规模N,最大迭代次数M,扰动因子α,降温速率λ,并令t=1,T=T0;
b) 评价粒子的适应度,找出当前最优位置存储于P0;
c) 根据式(7)进行高斯扰动,产生当前最优的替代值Pt′并根据Metropolis准则接受Pt′;
d) 根据式(3)、(6)计算参数r1、w,随机产生r2、r3、r4;
e) 根据式(5)更新第i个粒子的个体位置;
f) 评价粒子的适应度,找出当前最优位置并存储于Pt;
g) 根据式(8)、(9)退温并判断是否到达最大迭代次数,若满足则输出最优解,否则返回(c)。
T0=f(Pt)/ln 5
(8)
T=λT0
(9)
改进的正余弦算法流程图如图2。

图 2 SASCA算法流程图Fig.2 SASCA algorithm flow chart
3 算法测试
3.1 标准测试函数
为测试对比算法的性能,本文选取了10个不同的测试函数[17],分别用5种算法进行求解,其中f1~f5为单峰函数,f6~f10为多峰函数。
3.2 参数设计
为保证测试结果有效,10个测试函数设置相同的维数d=50,种群规模N=40,最大迭代次数M=1 000,其余参数设置如表1所示。

表 1 参数设置Tab.1 Parameter settings
3.3 测试结果
采用本文算法(SASCA),标准正余弦算法(SCA),改进的正余弦算法(ISCA),正弦算法(SA)以及基于模拟退火的蝙蝠算法(SABA),分别在10个不同的高维标准函数上进行测试。对每个算法独立运行50次并记录其均值、最优值、方差,以避免偶然性造成的误差。其中均值和最优值用于评价算法寻优精度,标准差用于衡量算法的鲁棒性。5种算法运行结果如表2所示。
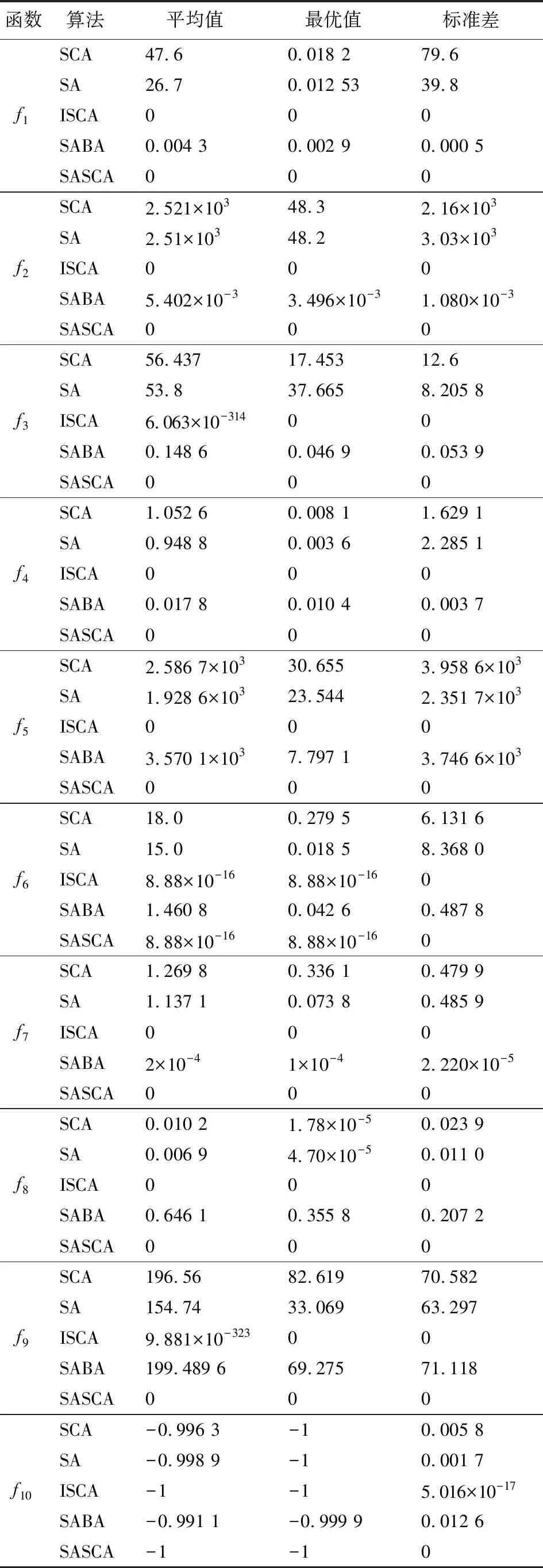
表 2 5种算法的运行结果Tab.2 The running results of five algorithms
从表2可以看出:对于单峰函数f1~f5,ISCA算法和SASCA算法在求解5个函数时,基本都找到真实最优值,且标准差皆为0,鲁棒性强;对于多峰函数f6,虽未求得真实最优值,SASCA算法和ISCA算法也有更高的寻优精度,比其余算法提高了10多个数量级。对于多峰函数f7~f10,ISCA算法在求解函数f7和f8时可以直接找到真实最优解,但在函数f9和f10求解中寻优精度和算法鲁棒性略为逊色,而SASCA算法在求解时都找到真实最优值。表明改进的算法对单峰、多峰函数都具有更高的寻优精度和鲁棒性。
为比较不同算法的收敛速度,图3给出了5种算法求解不同测试函数的迭代曲线图,其中f2、f6、f7、f8的迭代曲线较为集中,因此目标函数优化值用以10 为底的对数形式表示,以便更显著的区分5种算法的迭代曲线。从图3(a)~(j)可以看出:SASCA算法能快速收敛到最优值,ISCA算法次之,其余3种算法在迭代500次之后仍未收敛。特别是对于函数f2~f4和f6~f9,其余3种算法都陷入了局部最优且无法收敛到最优解。因此,本文的改进算法收敛速度比其余算法更优,能更高效实现高维函数的求解。

(a) f1函数
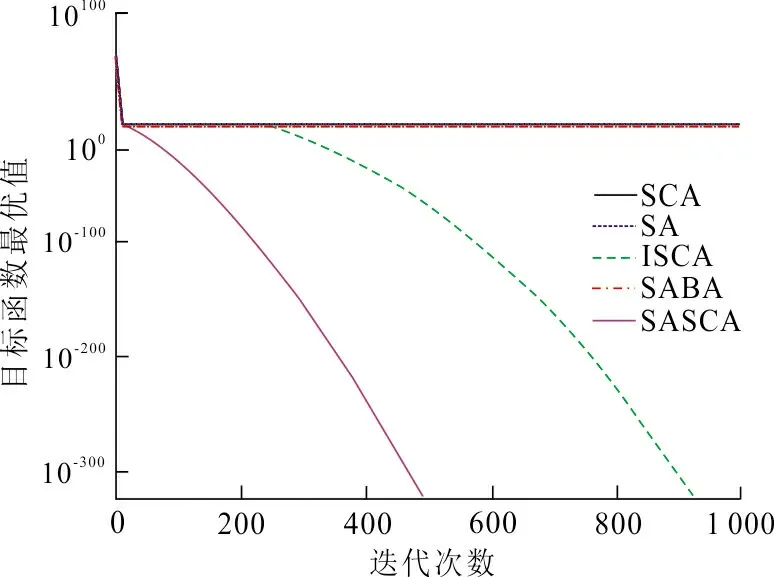
(b) f2函数
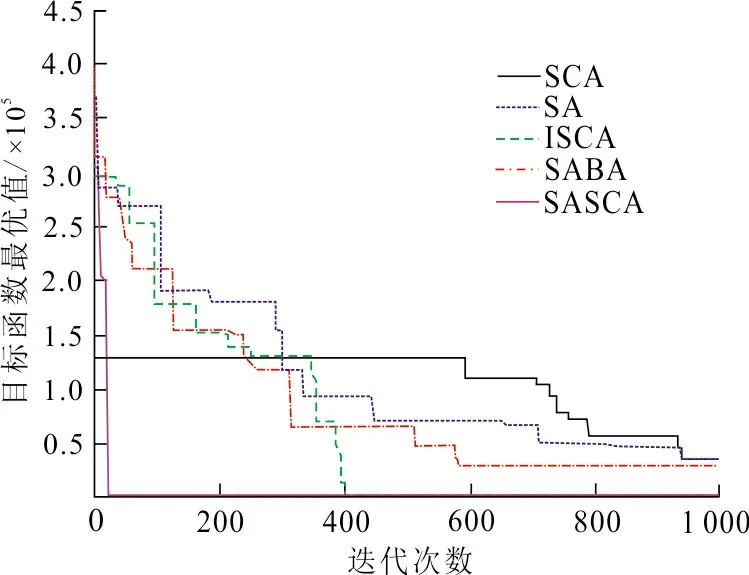
(c) f3函数

(d) f4函数
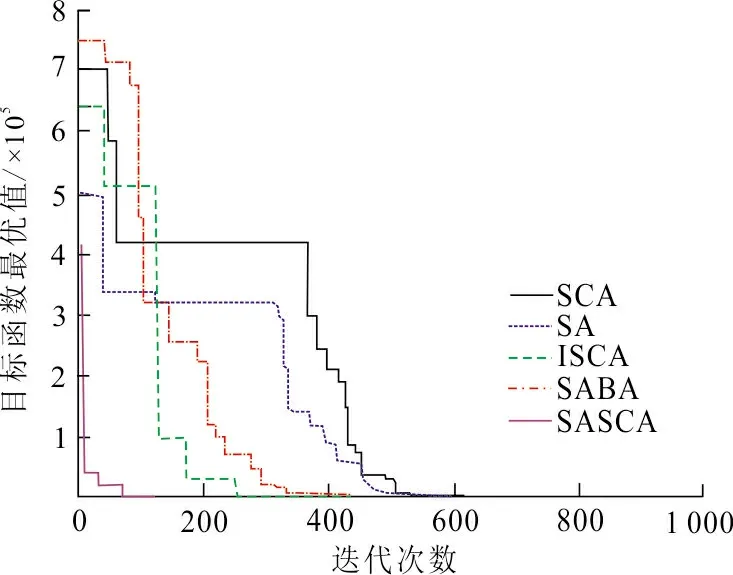
(e) f5函数

(f) f6函数
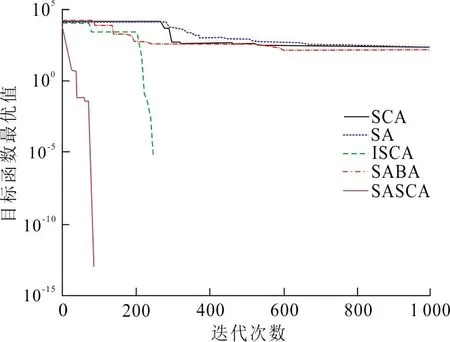
(g) f7函数

(h) f8函数

(i) f9函数

(j) f10函数图 3 5种算法迭代曲线Fig.3 Iterative curve of five algorithms
3.4 统计分析
为进一步比较5种算法的优劣性,采用t检验法比较分析 SASCA 与 SCA、SA、ISA 、SABA算法的性能。5种算法在每个测试函数上都独立运行50次,因而都有50个样本。t检验使用自由度为98,显著性水平为0.05的双尾检验,检验结果如表3所示。表3中,“+”表示对于同一测试函数,SASCA算法显著性优于本列算法;“~”表示对于同一测试函数,SASCA算法与本列算法显著性相同。
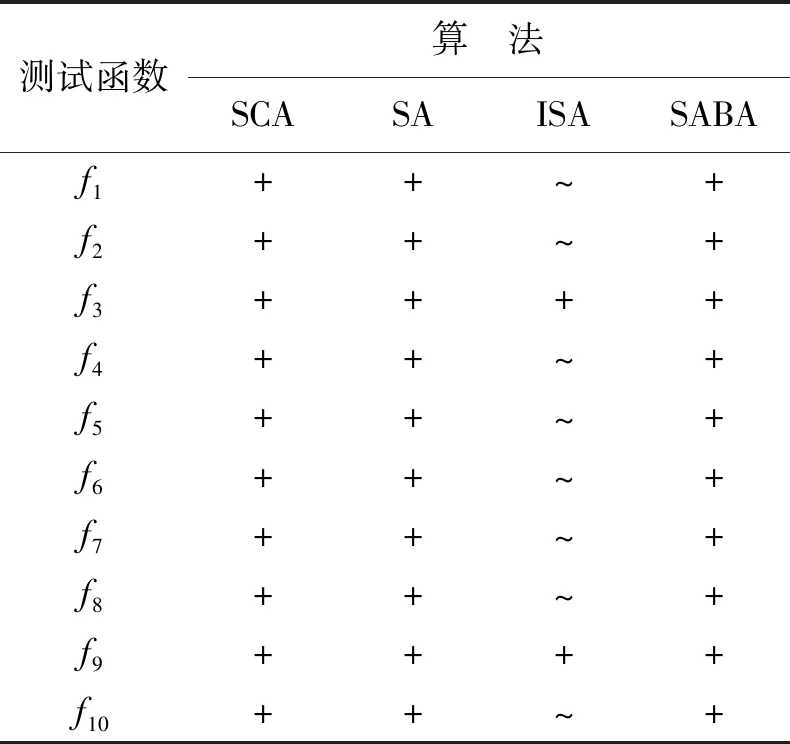
表 3 SASCA算法与其他算法的t检验Tab.3 t-test of SASCA algorithm and other algorithms
从表3可以看出,SASCA算法的显著性优于SCA、SA、SABA算法。除f3和f9外的其余8个函数,ISA算法与SASCA算法显著性相同;对于函数f3和f9,SASCA算法显著性更优。从统计的角度出发,在大部分测试函数上,SASCA算法的显著性优于其他4种算法。
4 结 语
通过将高斯扰动和模拟退火机制引入正余弦算法,在算法迭代的后期增加种群多样性以增强算法全局搜索能力。同时,设置自适应调整的参数r1以及对数递减的惯性权重,实现全局搜索与局部开发平衡,以提高算法寻优精度和收敛速度。5种算法仿真结果表明,基于模拟退火的正余弦算法寻优精度更高,收敛速度更快。统计检验的结果进一步验证了改进算法的有效性。

