中立型随机时滞微分方程截断Milstein数值解的强收敛性
李 琛,尤苏蓉
(东华大学 理学院,上海 201620)
0 引 言
随着现代科学技术的迅速发展,中立型随机时滞微分方程(neutral stochastic delay differential equation,NSDDEs)已被广泛应用于化工和空气动力学等工程领域及人口动力学领域[1-4]。NSDDEs在系数满足局部Lipschitz条件、线性增长条件和中立项的压缩映射条件下存在唯一解[5]。但是,NSDDEs很难求精确解,一般用数值解近似代替精确解[6-7],所以其数值解的研究也得到人们越来越多的重视。
在方程满足线性增长条件时,数值解的经典算法如Euler-Maruyama法、倒向Euler-Maruyama法被广泛应用于微分方程的求解。这些形式的数值解一般会有较好的收敛性、稳定性等性质[8-11]。不过,当方程系数具有非线性特征时,这些性质会受到削弱,甚至数值解的收敛性也得不到保证。而截断思想可用于构建带有非线性系数方程的数值解。文献[12]首次引入截断Euler-Maruyama数值方法,用于研究随机微分方程;文献[13-14]进一步将其应用于随机时滞微分方程,使得数值解依矩强收敛于精确解,并且有较好的收敛率。但是,在很多领域仍然需要数值解有更高的收敛精度。文献[15]中首次引入Milstein方法用于研究随机微分方程,使其数值解有更高的收敛精度;文献[16-17]将此方法进一步引入带有高度非线性系数的随机微分方程。不过,带有非线性系数的NSDDEs在Milstein方法下是否收敛,还未有定论。本文将针对此问题加以研究,在使用与精确解相同假设的情况下,证明数值解是Lp强收敛的。
1 问题背景
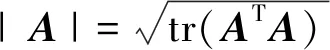
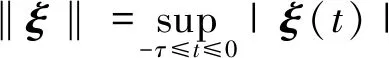
向量x(t)、x(0)、ξ对应的集合表示分别记为x(t)、x(0)及ξ。
考虑非线性中立型随机时滞微分方程
(1)
初值为
x(0)={ξ(θ):-τ≤θ≤0}∈
式中:
f:C([-τ,∞),Rn)×C([-τ,0],Rn)→Rn
g:C([-τ,∞),Rn)×C([-τ,0],Rn)→Rn×m
f(x,y)、g(x,y)为方程(1)的非线性系数;N:Rn→Rn为中立项;
B(t)=(B1(t),B2(t),…,Bm(t))T
是m维布朗运动。
假设1(局部Lipschitz条件) 对任意给定的实数Z≥1,存在常数Lz>0,使得

成立



c1|x|r≤V(x)≤c2|x|r
(2)
∃λ>0和p>2,成立
LV(x,y)=(x-N(y))Tf(x,y)+
(3)
假设3(压缩映射) 存在常数a∈(0,1),使得∀x,y∈Rn,成立
|N(x)-N(y)|≤a|x-y|
并且有N(0)=0,|N(x)|≤a|x|。

证明应用标准截断技术,由Lipschitz条件及压缩映射,对任给的初值,当t∈[-τ,τe)时,有一个局部最大解x(t)。设τe为爆破时间,且让k0>0充分大,使得
对任意的整数k>k0,定义停时
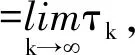
可以得到方程(1)的积分形式
x(t)=ξ(0)-N(ξ(-τ))+N(x(s-τ))+
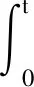
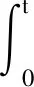
(4)
再令k=a/(1-a),由不等式 |x+y|p≤(1-k)1-p|x|p+k1-p|y|p及假设3,得
(5)
于是,由式(4)、(5)得
(6)
由假设2,Young不等式,对式(6)两边取期望E(·),得
(7)
∀t∈[0,T],式(7)右边的和是单调递增的。因此有
(8)
对式(8)用Gronwall不等式 ,可得
E|x(T∧τk)p|≤

这意味着kpP(τk≤T)≤C0。令k→∞,则
由于T是任意的,所以得τk=∞ a.s.,解的存在唯一性得证。同理可得

2 截断Milstein数值解及其强收敛性

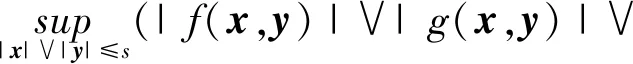
|gi(x,y)|)≤φ(s)
(9)
式(9)中,设i=1,2,有
设φ-1是φ的反函数,φ-1:[φ(0),∞)→R+是一个严格增连续函数。存在常数Δ*∈(0,1)及一个严格减函数ψ:(0,Δ*]→(1,∞),∀Δ∈(0,Δ*],使得

(10)
由式(9)、式(10),对给定的步长Δ∈(0,1),定义截断方程
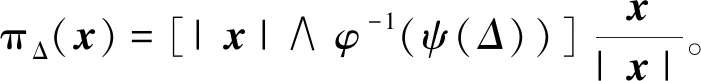
可以看出

φ(φ-1(ψ(Δ)))=ψ(Δ)
(11)
假设T=MΔ,τ=N*Δ,设置tk=tΔ,Y(0)=ξ(0)。定义离散的截断Milstein数值解为:当k=-N*,-N*+1,…,0 (N*∈N)时,Y(tk)=ξ(tk)。
当k>0时,
式中:
Bk=B(tk),ΔBk=Bk+1-Bk
定义连续时间Milstein数值解如下:当t∈[-τ,0]时,y(t)=ξ(t);当t>0时,
式中:
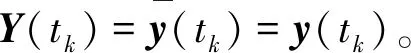
方程截断后的系数仍应满足假设2。为此,在假设2的基础上引入一个更强的假设:
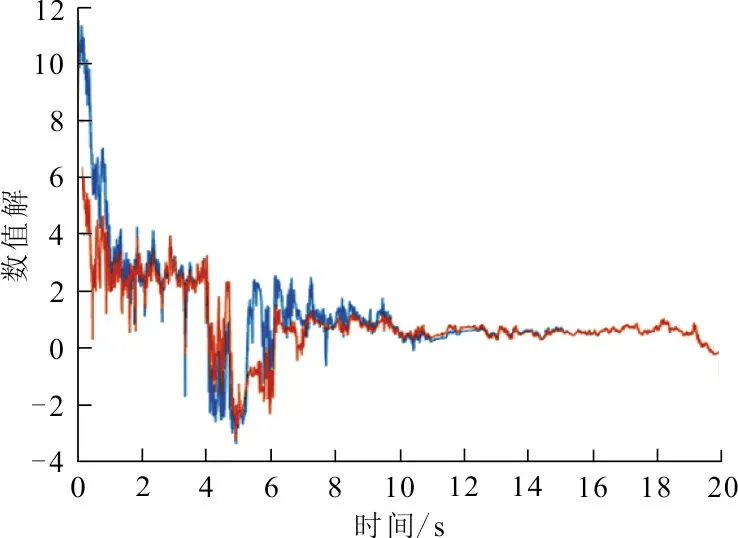
假设4 设λ>0,p≥2,∀0 λ(1+|x|2+|y|2) (12) 若令H=1,则式(12)退化为假设2。 定理1 若假设4成立,∀Δ∈(0,Δ*],有 λ(1+|x|2+|y|2) (13) 证明∀Δ∈(0,Δ*],由式(10)得 φ-1(ψ(Δ))≥φ-1(ψ(Δ*))≥1 式(13)的证明分2种情况: (ⅰ) 当|x|∨|y|≤φ-1(ψ(Δ))时, (πΔ(x)-N(πΔ(y)))Τf(πΔ(x),πΔ(y))+ λ(1+|πΔ(x)|2+|πΔ(y)|2)≤ λ(1+|x|2+|y|2) (ⅱ) 当|y|∨|x|>φ-1(ψ(Δ))时,由式(13)得 定理得证。 假设5(初值条件) 若存在常数K0>0,使得∀s,t∈[-τ,0],有 |ξ(t)-ξ(s)|≤K0|t-s| 引理2 若假设1~3,假设5成立,∀Δ∈(0,1),有 (14) 证明固定任给的Δ,存在唯一的整数k>0,使得tk≤t 由式(10)得,当Δ→0时, 即证得式(14)成立。 引理4 若假设1~3成立,对t∈[0,T]及∀T>0,有 (15) 证明固定任给的Δ∈(0,Δ*),由It公式,Young不等式及不等式得 N(ξ(-τ))|p+ (16) 根据式(11),Young不等式,对式(16)中的几个部分分开推导: CΔp/2(ψ(Δ))2p≤ CΔP/2(ψ(Δ))2p≤ 再根据引理3,式(10)、式(11)得 CTΔp/4(ψ(Δ))3p/2≤ CTΔp/4(ψ(Δ))3p/2≤ 将以上各拆分部分带入式(16),应用Gronwall不等式,得 (17) 同理可得 (18) 因为式(17)、式(18)对所有的Δ∈(0,Δ*]成立,引理得证。 引理4证明了NSDDEs截断Milstein数值解的矩有界性。最终定理需要利用方程数值解的相关停时,为此引理5、6将定义方程数值解的相关停时。 引理5 若假设1~3成立,对任给的实数Z>‖ξ‖,定义停时 σz=inf{t≥0:|x(t)|≥Z} 证明∀t∈[0,T],有 引理6 若假设1~3成立,对任给的实数Z>‖ξ‖,定义停时 σΔ,z=inf{t≥0:|y(t)|≥Z} 证明: (19) 由定理1,得 (20) 对式(20)右边分开推导 (ⅱ) 由式(9)得 (ⅲ) 由引理3得 CTΔ1/2(ψ(Δ))3≤C 将以上推导代入式(19),由Gronwall不等式得 定理2 若假设1~5成立,当q∈[2,p)时,有 证明对停时σΔ,z,σz和x(T),y(T)定义 θ:=σΔ,z∧σz,eΔ(T):=x(T)-y(T) 由Young不等式,∀δ>0,成立 (21) 由定理1,引理2,得 E|eΔ(T)|p≤C (22) 由引理3,引理4,得 (23) 将式(22)、(23)代入式(21),得 E|eΔ(T)|q≤E(|eΔ(T)|qI{θ>T})+ (24) 定义截断函数如下:∀x,y∈Rn,有 假设Δ*足够小,使得φ-1(ψ(Δ*))≥Z,∀Δ∈(0,Δ*)。当|x|∨|y|≤Z成立时,有 对初值η(t)∈C([-τ,0],Rn),设 (25) 由假设1,得到Fz(X(t),X(t-τ)),Gz(X(t),X(t-τ))关于Lz是Lipschitz连续。当t≥0时,式(25)存在一个唯一全局解X(t),即有 x(t∧σz)=X(t∧σz) (26) (27) 由文献[12]中的结论 有 (28) 将式(26)、式(27)代入式(28),成立 因此有 E(|eΔ(T)|qI{θ>T})= E(|eΔ(T∧θ)|qΙ{θ>T})≤ 定理2得证。 考虑如下中立型随机泛函微分方程 设置初值为x(0)=ξ={cosθ+M:-1≤θ≤0}。 利用Matlab软件模拟了中立型时滞微分方程截断Milstein的数值解,结果如图1所示。图1中分别设置M为5(红色)和10(蓝色)。对于红色线段图,Δ=2-12,时滞为1。当t=4 097Δ时首次低于-3,发生截断。 图 1 中立型随机时滞微分方程截断Milstein数值解Fig.1 Truncated Milstein numerical solution of NSDDEs 本文研究了中立型随机时滞微分方程的数值解,用Milstein方法分析,说明了解析解的强收敛条件。通过一系列技巧对中立项及时滞项进行处理,最终得到截断Milstein数值解仍将保持强收敛的结论。由于篇幅的原因,后续将进一步发表其收敛阶数接近于1,并且将进一步研究其稳定性的条件与相关性质。
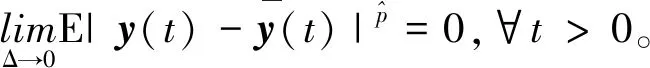
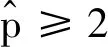


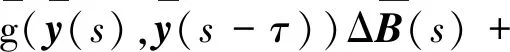
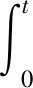
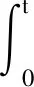
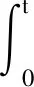
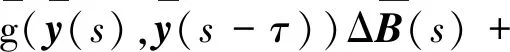
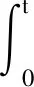
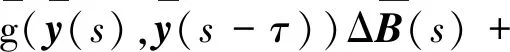

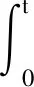
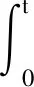
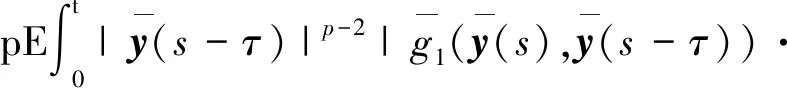
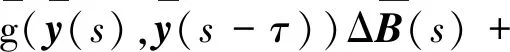

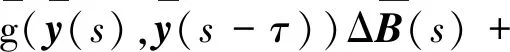

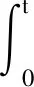
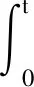
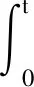

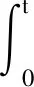




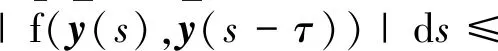

3 数值模拟
4 结 语

