不确定非线性切换系统的事件触发保成本有限时间H∞控制
张福燕,吴保卫
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
0 引 言
切换系统是由一系列子系统和一个确定的逻辑规则组成的混合系统,在网络控制、机器控制、化学控制等系统中应用广泛[1-3]。 稳定性是切换系统的一个基本属性,其中Lyapunov渐进稳定和指数稳定的研究最为广泛[4-5]。但在实际应用中,有时需要系统在短时间内运行稳定,即有限时间稳定。这一概念在20世纪50年代被Kamenkov提出[6]。关于切换系统在有限时间内的动态行为,文献[7]探究了切换系统的异步滤波有限时间有界的问题;文献[8]和文献[9]分别研究了执行器失效的线性系统和分数阶正切换系统的输入输出有限时间稳定问题。
过时间触发方案用于系统数据采样和信号更新,会造成系统资源的浪费。 为了节约资源,1994年提出了事件触发方案[10]。数据采样和信号更新是由“事件”是否触发决定的,减少了不必要的数据采样和传输。因此,对事件触发方案的研究至关重要[11-17]。
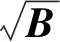
1 问题描述和预备知识
考虑不确定非线性切换系统
(1)
其中x(t)∈Rn,u(t)∈Rm,z(t)∈Rp分别表示系统(1)的状态向量,控制输入和控制输出;ω(t)∈L2[0,∞) 表示外部扰动,且满足‖ω(t)‖≤ν‖x(t) ‖,ν是非负常数;fσ(t)(x(t))∈Rn表示系统的非线性部分,且fσ(t)(0)=0,满足单边Lipschitz条件。

[ΔAσ(t),ΔBσ(t)]=Wσ(t)Hσ(t)(t)·
[E1σ(t),E2σ(t)]
(2)

假设1Bσ(t)是列满秩矩阵,即rank(Bσ(t))=m。
对于系统 (1),定义二次成本函数如下:
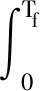
uT(t)Tσ(t)u(t)]dt
(3)
式中:Qσ(t) 和Tσ(t) 是对称正定矩阵。
定义1[12]如果存在常数τa>0和N0≥0,使得
式中:Nσ(τ,t)表示系统 (1) 在区间[τ,t) 上的切换次数;τa为平均驻留时间;N0为抖振界。
不确定非线性切换系统的事件触发方案定义如下:
δσ(t)xT(t)Nσ(t)x(t)}
(4)
式中:etk(t)=x(tk)-x(t);Mσ(t)和Nσ(t)是适当维数的对称正定矩阵;δσ(t)>0是给定的事件阈值;tk表示事件触发采样时刻。考虑状态反馈控制器
u(t)=Kσ(t)x(tk),t∈[tk,tk+1)
(5)
利用式(4)和式(5),不确定非线性切换系统 (1) 形成了不确定非线性切换闭环系统
(6)
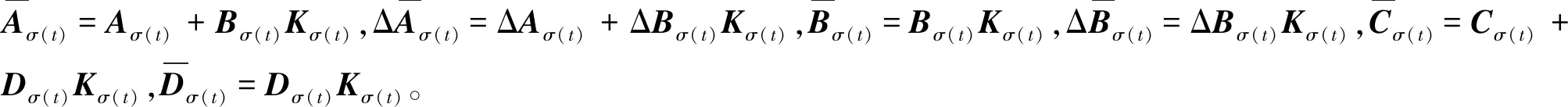
引理1[11]对于任意适当维数的实值矩阵X,Y和Ξ(t),且ΞT(t)Ξ(t)≤I,则∀λ>0,有
XΞ(t)Y+YTΞT(t)XT≤λXXT+λ-1YTY
定义2(单边Lipschitz条件[21]) 若存在常数ρ1i,使得∀x1(t),x2(t)∈Rn,有
〈fi(x1(t))-fi(x2(t)),x1(t)-x2(t)〉≤
ρ1i‖x1(t)-x2(t)‖2
成立,则称非线性函数fi(x(t)) 在域D(⊆Rn) 上满足单边Lipschitz条件,其中ρ1i是单边Lipschitz常数。
定义3(二次内积有界性质[21]) 若存在常数ρ2i,ρ3i,使得∀x1(t),x2(t)∈Rn,有
(fi(x1(t))-fi(x2(t)))T(fi(x1(t))-
fi(x2(t)))≤
ρ2i‖x1(t)-x2(t)‖2+ρ3i〈x1(t)-
x2(t),fi(x1(t))-fi(x2(t))〉
成立,则称非线性函数fi(x(t))在域D上是二次内积有界的,其中ρ2i,ρ3i是已知常数。
注1 文中的ρ1i,ρ2i,ρ3i是任意常数,当ρ1i>0,ρ2i>0,ρ3i=0 时,非线性函数即满足Lipschitz条件,但反之不成立。
定义4[7]给定正常数c1≤c2及Tf,以及正定矩阵R、切换信号σ(t),若
xT(t0)Rx(t0)≤c1⟹xT(t)Rx(t)≤c2,
∀t∈[0,Tf]
成立,则称不确定非线性切换闭环系统(6)关于(c1,c2,Tf,R,σ(t))是有限时间有界的。
定义5[13]不确定非线性切换闭环系统(6)是有限时间有界的,且具有H∞性能指标γ>0,需要满足:
(ⅰ) 不确定非线性切换闭环系统(6)关于(c1,c2,Tf,R,σ(t))是有限时间有界的;
(ⅱ) 在零初始条件下,控制输出z(t)满足
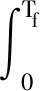
∀t∈[0,Tf]
定义6[13]考虑在事件触发方案(4)条件下的不确定非线性切换系统(1)。如果∃J*≥0和u*(t),使得不确定非线性切换闭环系统(6)是有限时间有界的,且具有H∞性能指标γ>0,并且切换系统 (1)的保成本函数(3)满足J≤J*,则J*称为切换系统(1)保成本的上界,u*(t)称为保成本控制器。
2 主要结果
证明切换闭环系统(6)是有限时间有界的,且具有H∞性能指标γ>0,并基于此找到切换系统(1)的保成本上界J*。

Ω=
0
(7)
(8)
(9)
(10)
且切换信号满足
(11)
式中:
则不确定非线性切换闭环系统(6)关于(c1,c2,Tf,R,σ(t))是有限时间有界的,且具有H∞性能指标γ,切换系统(1)的保成本上界为
J*=exp(αTf)γ2d[1+N(μ-1)μN]+
[1+N(μ-1)μNexp(αTf)]Vσ(0)(x(0))
(12)

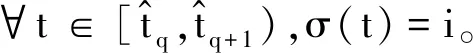
Vσ(t)(x(t))=xT(t)Pσ(t)x(t)
(13)
分3步证明此定理。
1) 证明切换闭环系统(6)是有限时间有界的。
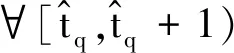
(14)
由定义2和定义3,有下列不等式成立:
ε2i(fi(x(t)))Tfi(x(t))≥0
令
则
(15)
其中
由式(7)Schur补,得Ω1<0,由事件触发方案(4)知
(16)
因此
(17)
(18)
同理,在其他事件触发子区间上也有类似于式(18)的形式,即有
(19)
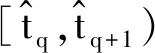
另一方面,由式(8)可得
(20)
结合式(18)和式(20)可得
t∈(0,Tf)
(21)
由定义1知,Nσ(τ,t)≤N。因此,由式(20)和式(21)知
(22)
由‖ω(t)‖≤ν‖x(t)‖,可得
令L=max{ωT(t)ω(t)},t∈[0,Tf],则有

从式(22)得
(23)
式(23)若成立,必有
也就是说,若‖ω(t)‖≤ν‖x(t)‖,则∃d满足
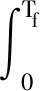
(24)
由式(22)和式(24)得
V(x(t))<μNσ(0,Tf)exp(αTf)·
[Vσ(t0)(x(t0))+γ2d]
(25)
另外,
(26)
同理
(27)
由定义1,并结合式(10)与(11)可得
xT(t)Rx(t)≤c2
(28)
因此,不确定非线性切换闭环系统(6)关于(c1,c2,Tf,R,σ(t))是有限时间有界的。
2) 不确定非线性切换闭环系统(6)具有H∞性能指标γ>0。
由式(6)知
[Ci+DiKiDiKi00]η(t)
(29)
由Schur补和式(7)可得类似于式(15)的情形,再根据式(16)得
αxT(t)Pix(t)-zT(t)z(t)
(30)
其中γ>0,故有
(31)
在零初始条件下,令t→Tf,即得

由定义5知,不确定非线性切换闭环系统(6)具有H∞性能指标γ。
3) 求证保成本函数的上界J*。
由式(7)和式(13)~(16)知
(32)
利用式(20)、(25)和(32),不确定非线性切换闭环系统(6)的保成本函数满足
uT(t)Tσ(t)u(t)]dt≤
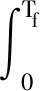
exp(αTf)γ2d+Vσ(0)(x(0))+
exp(αTf)γ2d[1+N(μ-1)μN]+
[1+N(μ-1)μNexp(αTf)]·
Vσ(0)(x(0))
(33)
由此得到式(12)。定理1得证。
注2 由于定理1中矩阵不等式(7)是非线性的,无法利用Matlab求解。因此,引入定理2,将其转化为线性矩阵不等式,并利用LMI工具求解保成本有限时间H∞状态反馈控制器增益Ki及保成本上界J*。

(34)
成立,且切换信号的平均驻留时间满足式(11),其中
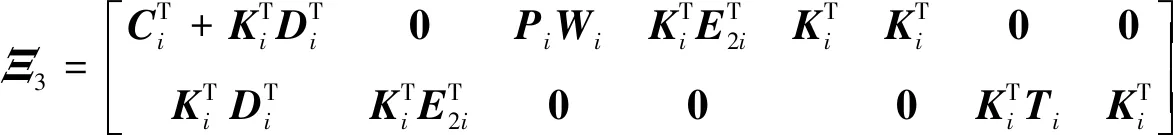
Ξ4=diag[-ε2iI,-γ2I]
Bi是列满秩,则相关的控制器(5)的增益矩阵为
(35)
保成本函数J≤J*,上界J*满足式(12)。
证明根据定理 1,令Li=PiBiKi,由Schur补知,不等式矩阵式(7)与(34)等价。由此,在事件触发方案下,可利用线性矩阵不等式得到保成本有限时间H∞状态反馈控制器增益矩阵Ki和保成本上界J*。定理2得证。
为了说明利用事件触发方案(4)进行数据采样时,不会发生Zeno行为,有如下定理:
定理3 考虑事件触发方案(4)和切换闭环系统(6),事件触发执行区间tk+1-tk(∀tk)的下界为
(36)

χ6=max{‖E1i‖},χ7=max{‖E2iKi‖}
证明为了便于求导,定义‖·‖为|·|。eET(t)=etk(t),且
∀t∈[tk,tk+1),k∈N
由式(2)、(4)和(6)得
(1+Λ1y(t))(Λ2+Λ3y(t))
(37)
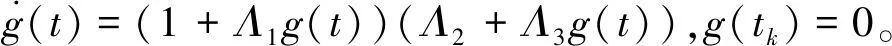
y(t)的值为0到χ11,因此事件触发执行区间的下界g(T)=χ11的解为T=t-tk,即得式(37)。


(38)
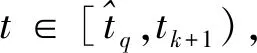
(39)
已知y(tk)=g(tk)=0,类似于情形(1),即得式(36)。从式(36)中可知T>0,即可避免Zeno行为。定理3得证。
3 数值实例
考虑具有2个子系统的非线性切换系统(1),其中
E21=E22=I,H1(t)=H2(t)=sinx(t)
利用LMI工具箱解线性矩阵不等式(8)~(10)和式(34),得保成本上界J*=58.200 9,矩阵P1,P2分别为
状态反馈控制器增益为
相应的事件触发参数为

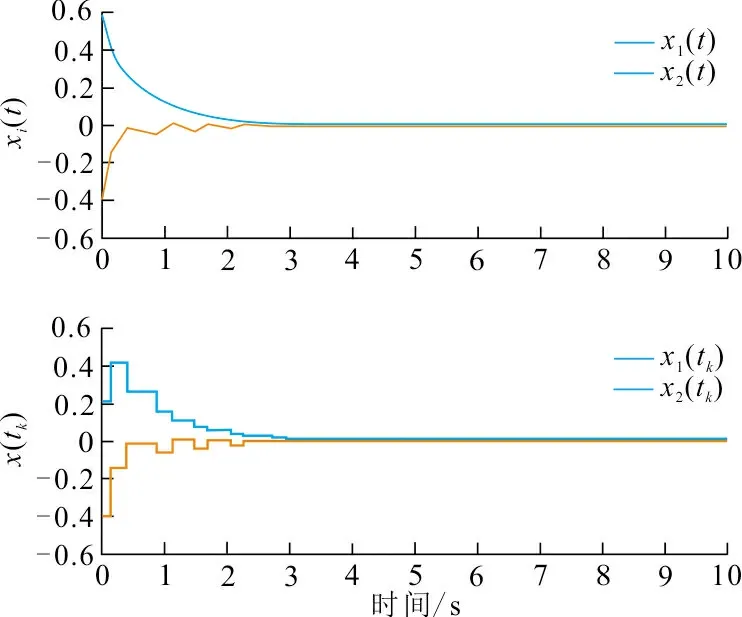
图 1 状态运动轨迹Fig.1 The trajectories of states

图 2 切换信号σ(t)Fig.2 The switching signal σ(t)
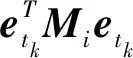
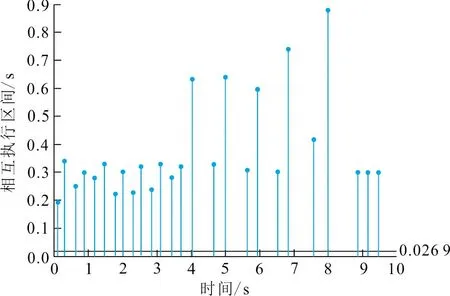
图 3 事件触发相互执行区间Fig.3 Inter execution intervals of theevent-triggered

图 4 触发界Fig.4 The triggered boundary
注3 在文献[13]中,作者研究了具有扰动和不确定因素的切换系统在事件触发采样机制下的保成本有限时间H∞控制问题,然而其并未考虑非线性因素对系统的影响。本文在[13]的基础上,进一步讨论了切换系统(1)包含有非线性因素的情况,利用定义2、3,将非线性函数线性化,证明了系统(1)在事件触发方案下是有限时间有界的且具有H∞性能指标γ,并且找到了保成本的上界J*。文献[13]可作为本文的一个特例,本文所考虑的系统更具有一般性。
4 结 语
讨论了不确定非线性切换系统的事件触发保成本有限时间H∞控制问题。在事件触发方案下,得到了不确定非线性切换闭环系统是有限时间有界的且具有H∞性能指标γ的充分条件,并找到了切换系统的保成本上界J*和状态反馈控制器u(t)的设计方案。证明了Zeno行为能够被避免,由一个数值例子验证了结论的有效性。

