部分截断Euler-Maruyama数值方法的保正性
汪 勇,胡良剑
(东华大学 理学院,上海 201620)
0 引 言
截断Euler-Maruyama(EM)方法是MAO在提出的一种新的显式方法[1],用于研究高度非线性随机微分方程数值解,并证明了该数值方法的Lp收敛性。之后,文献[2]从步长的角度出发,改进了部分严格的限制性条件,并确保截断EM方法的收敛性和稳定性仍然成立。文献[3]针对有限时间强收敛性的假设条件进行了分解,文献[4]从稳定性的角度出发,研究了部分截断EM方法。之后,部分假设条件的限制被放松[5],文献[6]对假设条件做了进一步优化。随后,出现了更多关于随机微分方程数值解的相关研究[7-10],并且出现带时滞的随机微分方程数值解相关理论研究[11]。
本文考虑一个标量随机微分方程
dx(t)=b(x(t))dt+σ(x(t))dW(t),t≥0
(1)
式中:b和σ为局部Lipschitz连续函数;W(t)为一维布朗运动;初值x(0)=x0>0。在许多包含数量问题的实践中,比如对股票市场的研究以及生物种群模型的研究时,需要模型的解取正值。因此,当随机微分方程(1)有一个正解,如何构造它的数值近似,以保证数值解也为正是主要研究问题。
对于数值解保正性的研究已经有了一些已知的结论[12-14]。文献[15]证明了EM方法不能使任何一维随机微分方程数值解保持正性。文献[16]使用Lamperti变换,对扩散系数严格为正的原始随机微分方程进行了变换,变为
dx(t)=F(x(t))dt+c0dW(t)
并采用隐式欧拉法对变换后的随机微分方程进行离散化,使得在适当的假设条件下,随机微分方程的数值解收敛到真实解。文献[17]提出了一类在适当步长和权值下保正性的平衡隐式方法,收敛条件需满足线性增长条件。
文献[18]提出了Cox-Ingersoll-Ross(CIR)金融模型
x(0)=x0
且该模型在实践中有所应用。
为了研究更普遍的具有保正性的随机微分方程数值解问题,而不是特例,本文从一般的随机微分方程出发,构造一个显式对数EM格式。采用部分截断EM方法,在保证随机微分方程数值解收敛性的同时,能够保持其正性。
1 预 备
由于只考虑随机微分方程(1)的正解,因此假设系数b和σ为定义在R+上的实值函数,同时,假设b、σ为Lipschitz连续的。对于c∈R+,引入标量函数
定义
假设1 假设下列Feller条件

(2)
成立。由文献[19]中命题5.17和5.18的相关结论可知,条件(2)等价于随机微分方程(1)具有唯一强解x(t),t≥0,并且其轨道包含在R+中,即
P(x(t)∈(0,∞),t≥0)=1
(3)
也就是说,假设条件(2)成立,那么∀t≥0,随机微分方程的解都为正。希望找到一般的数值方法构造式(2)在Feller条件下正的近似解。首先,采取对数变换,令
y=φ(x)=lnx,x∈R+
应用伊藤公式,得到转化后的关于y(t)的随机微分方程
dy(t)=f(y(t))dt+g(y(t))dW(t)
(4)
其中y(0)=y0=lnx0,并且
(5)

定理1 如果随机微分方程(1)满足假设1条件,那么随机微分方程(4)在有限时间存在非爆炸唯一解,即
P(y(t)∈(-∞,∞),t≥0)=1
证明令
以及
此时,方程(4)的解的非爆炸性仍然可以用Feller-条件证明,即
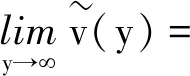
又y=ln(x),则可知
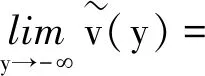
以及

可以得到,随机微分方程(4)的解以概率1有限存在,即在有限时间不会趋于无穷。
引理1[3]假设方程(4)的系数为局部Lipschitz连续的,且满足∀γ≥1,p>2,∃Kγ≥0,使得
(6)
任给n>0,考虑随机微分方程
dyn(t)=fn(yn(t))dt+gn(yn(t))dW(t)
(7)
式中:
fn(y)=f((|y|∧n)sgn(y))
gn(y)=g((|y|∧n)sgn(y))
由于随机微分方程(4)的系数满足条件(6),随机微分方程(7)的系数满足全局Lipschitz条件,所以当n→∞时,存在唯一的解yn(t),依概率收敛到随机微分方程(4)的精确解y(t)[3]。应用截断EM方法于方程(7),可以得到一个数值逼近yΔ,n(t)在Lp意义下强收敛到yn(t)。因此,∀Δ,∃nΔ,使得yΔ,nΔ(t)依概率收敛到y(t)。
然而,经过对数变换后,随机微分方程(4)的系数为超线性增长甚至指数增长,给数值方法的构建带来新的困难,所以基于全局Lipschitz条件或者多项式增长条件下的强收敛定理不再适用。
2 数值解的收敛性和保正性
2.1 相关引理及假设
∀T>0,给定有限时间间隔[0,T],考虑分割0=t0 这里p∈[1,∞),则 引理1说明EM逼近在强或者弱Lp意义下都可能发散,所以需要讨论转化后的随机微分方程数值解的指数可积性。因此,当系数呈指数增长同时需要满足指数可积性的附加要求时,现有的强收敛性结论在一些情况下将不适用。本文将重点讨论截断EM方法,该方法因其简单而在实践中广受欢迎。但是,即使这种方法简单,仍然需要处理指数增长所带来的影响。故需要引入一些附加条件,使得截断EM方法在随机微分方程的系数为指数增长时仍然收敛到其真实解。对随机微分方程(4)的系数给出假设条件。首先假设随机微分方程(4)的系数能被表示为 f(y)=F1(y)+F(y),g(y)=G1(y)+G(y) (8) 假设2 假设系数F1、F、G1、G满足如下条件:∃L1>0以及γ>0,使得 |F1(x)-F1(y)|∨|G1(x)-G1(y)|≤ L1|x-y| (9) 以及 |F(x)-F(y)|∨|G(x)-G(y)|≤ L1|x-y|(1+|x|γ+|y|γ) (10) 其中x,y∈R。 由式(9)可得到系数F1和G1满足线性增长条件,即存在常数K1,使得 |F1(y)|∨|G1(y)|≤K1(1+|y|) (11) 其中y∈R。 |G(x)-G(y)|2≤L2|x-y|2 (12) 其中x,y∈R。 假设4 假设存在常数p′>p以及K2>0,使得 首先,定义一个在[1,∞)→(0,∞)的严格增函数μ,使得当t→∞时,μ(t)→∞,且 (13) μ的逆函数μ-1为定义在[μ(1),∞)→(0,∞)的严格增函数。给定一个严格递减函数h:(0,1]→[μ(1),∞),且满足 定义πΔ为R到闭区间{x∈R:|y|≤μ-1(h(Δ))}上的映射,且 πΔ(y)=[|y|∧μ-1(h(Δ))]sgn(y) 则可以得到 dyΔ(t)=fΔ(yΔ(t))dt+gΔ(yΔ(t))dW(t) (14) 且有 FΔ(y)=F(πΔ(y)),GΔ(y)=G(πΔ(y)) 则 fΔ(y)=F1(y)+FΔ(y) gΔ(y)=G1(y)+GΔ(y) 由式(13)可以得到 |FΔ(y)|∨|GΔ(y)|≤μ(μ-1(h(Δ)))=h(Δ) (15) 应用EM方法到式(14),可以得到 yΔ(tk+1)=yΔ(tk)+fΔ(yΔ(tk))+ gΔ(yΔ(tk))ΔWk (16) 式中:k=0,1,…,N-1,ΔWk=W(tk+1)-W(tk)。令yΔ(0)=y0,定义式(16)的连续形式为 (17) 接下来,证明随机微分方程(4)的数值解yΔ(t)和精确解y(t)的指数可积性。 假设5 假设∀m≥1,存在常数Km(不依赖于p和y),使得 Kmpm,∀p>2,y∈R (18) 其中m与Km之间存在一定关系,可以理解为当m取较小值时,Km更趋向于取较大的值。 定理2 若假设5成立,且m<2,则对任意正常数q,方程(4)的精确解y(t)满足 (19) 证明对yp(t)应用伊藤公式得到 这里仅考虑p为正整数,令R>|y(0)|,τR=inf{t∈[0,T]:|y(t)|≥R},则可推导出 使用Gronwall不等式,有 exp(Cpt)≤Cp·(2p)mp 由τR的定义知 R2pP(τR≤t)=E((y(τR))2pI{τR≤t})≤ E(y2p(t∧τR))≤Cp·(2p)mp 因此,可以得到 P(τ∞>t)=1 由Jensen不等式,有 E|y(t)|p≤(E(y2p(t)))1/2≤ Cp(2p)mp/2≤Cppmp/2 可知,∀q>0,有 当m<2时,由斯特林公式,可以得到 E(exp(q|y(t)|))<∞ 接下来需要证明截断EM数值解仍然为指数可积的。 定理3 若假设5成立,则∀Δ∈(0,1],p>2,有 Km(pm+|y|) (20) 证明当|y|≤μ-1(h(Δ))时,式(20)显然成立。当|y|>μ-1h(Δ))时,有 (21) 又由式(18),可知 πΔ(y)F(πΔ(y))≤Kmpm (22) 将式(22)代入式(21),得 引理4[4]在假设5条件下,∀Δ∈(0,1],随机微分方程(4)的截断EM数值解为指数可积的,即 E(exp(q|yΔ(t)|))<∞,∀q>0 (23) 因此可得 (24) 证明由引理5可知,∃Δ*∈(0,1],使得 (25) 给定Δ∈(0,Δ*],∀t∈[0,T],存在唯一的k≥0,使得tk≤t≤tk+1,有 由式(25)可得 又因为Δ1/4h(Δ)≤1,于是进一步可得 定理5 若假设5成立,∀q>0,m<2,随机微分方程(4)的截断EM数值解yΔ(t)满足 证明由It公式和伊藤积分的性质,可得 因此,可以得到 使用Gronwall不等式,有 因此,∀t>0,可以得到 E((yΔ(t))2p)≤Cppmp 由Jensen不等式可得 E|yΔ(t)|p≤Cppmp/2,m<2 因此,∀Δ∈(0,1],结合斯特林公式,可以得到截断EM数值解的指数可积性。 定义 τR=inf{t∈[0,T]:|yΔ(t)|≥R} (26) 由于已经得到随机微分方程数值解和精确解的指数可积性的相关结论,进而可以得到 (27) 引理6[5]若假设2,3,4成立,则随机微分方程(4)的截断EM数值解yΔ(t)强收敛到其精确解,即 (28) 定理6 若假设5成立,则随机微分方程(1)的数值解xΔ(t)=exp(yΔ(t))将强收敛到其精确解,即 (29) 证明由均值定理可得 E|x(t)-xΔ(t)|q= E|exp(y(t))-exp(yΔ(t))|q≤ E|exp(y(t))+exp(yΔ(t))|q·|y(t)- yΔ(t)|q≤ [E|exp(y(t))+exp(yΔ(t))|2q]1/2· [E|y(t)-yΔ(t)|2q]1/2 由引理5、引理6以及指数可积性结果,可以得到收敛性结果,并且数值解保持了原解的正性。 基于Cox-Ingersoll-Ross(CIR)模型,考虑更为一般的随机微分方程模型 dx(t)=k(λ-x(t))dt+θ·(x(t))αdW(t) (30) (31) 可以得到F1(y)=y, G1(y)=0,G(y)=θexp(-(1-α)y) 易知假设2成立,对于假设3,可得 当p′>2时成立。对于假设5,由于2(1-α)<1,∀y>0,有 因为 则存在常数-M,对y<(-M∧-1),使得 令 则 求解H′(y0)=0,有 因此,存在正数Km,使得 本文在一定条件下,将随机微分方程的系数拆分为满足线性增长的部分和不满足线性增长条件的部分。应用部分截断EM的方法,对随机微分方程的系数采取只对不满足线性增长条件的部分进行截断的方式。通过对数变换的方法,证明了变换后的随机微分方程的数值解和解析解的指数可积性,进一步研究了随机微分方程数值解能保持原解析解的正性。

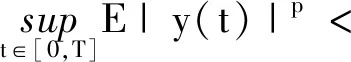

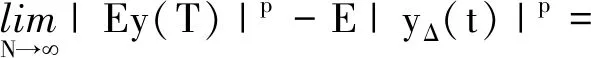

2.2 截断EM方法


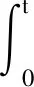
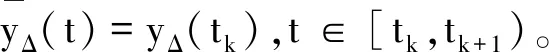
2.3 精确解的指数可积性

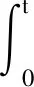

2.4 截断EM数值解的指数可积性


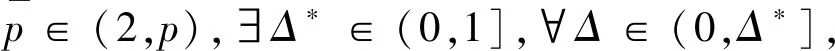





2.5 收敛结果及其正则性
3 数值算例



4 结 语

