学习策略的心理学研究及其对小学数学教学的启示

叶艳丽 喻平

摘要：心理学对学习策略的研究主要集中在学习策略的发展特点、使用效果、训练干预等方面。将这些研究的成果应用于小学数学教学，可以提出三条教学策略：教给学生专注于重要信息的策略，引导学生分析问题中的重要信息，以培养选择性注意策略;引导学生使用画图（包括示意图和概念图等）、类比、拓展等策略，以培养精加工策略;引导学生使用理解、联系、策略、反思等四类问题进行元认知自我提问，以培养元认知策略。

关键词：学习策略;选择性注意;精加工;元认知;小学数学

学习策略是指学生在学习活动过程中用以提高学习效率的学习规则和方法，它是认知策略和元认知策略在学习过程中的表现形式和具体运用。学习策略系统包括外显学习策略和内隐学习策略。外显学习策略指学生在学习过程中表现出来的使得学习有效的行为方式，如在预习、听课、复习、作业、应用、总结、考试等学习环节中的学习规则、方法或技巧。内隐学习策略指学生在学习过程中用来指导自己的注意、记忆、思维过程的技能，以及制订计划、选择策略、监视调节学习过程的技能。在心理学领域，大量关于学习策略的研究表明，在教学中有意识地培养或有目的地干预学习策略可以提高学生的学习效率。本文简要介绍一些研究成果，并提出几点对小学数学教学的启示。

一、心理学关于学习策略的一些研究

（一）学习策略的发展特点

儿童在记忆有关系的材料时，组织策略是不断发展的。Flavell从执行策略的基本能力、自发运用策略、激发策略运用的企图、策略运用时提取的效果等四个方面来分析儿童策略发展的主要阶段，提出儿童的策略发展（以复述策略为例）可以分为不会运用策略、运用时具有产生性缺损、成熟运用策略三个主要阶段。庞虹以词组联结为材料考查被试（一年级、三年级和五年级学生）记忆中组织策略的发展，结果表明，绝大多数一年级和三年级学生不能自发地运用组织策略;而五年级学生已能自发地运用组织策略，处于组织策略发展的成熟阶段。提供运用策略的指导，能够激发一年级和三年级学生运用组织策略，对三年级学生尤为明显。

认知策略是学习策略的重要组成部分。何进军等将认知策略分为注意集中、组织、理解、阐述、自我计检、目标想象和意象联系等七种类型，然后以此为依据编制问卷，对270名10—14岁（五至八年级）学生进行认知策略调查。结果显示，“优生”认知策略掌握优于“差生”;认知策略总体在年级上存在显著差异，具有随年级的升高逐步发展的趋势;六年级与七、八年级存在显著差异，说明从小学进入初中这一阶段可能是认知策略发展较为迅速的关键时期。而刘电芝等研究发现，不同年级、不同性别的小学生学习策略发展水平基本一致，即小学生学习策略发展水平并未随机体变量年龄、性别而不同，主要原因可能有两方面：一是我国学校以前长期忽略学习策略教学，导致未出现学习策略随知识的积累而提高的状况;二是小学生对学习策略的掌握还处于外控状态，主要受外部因素的影响。

陈英和等采用实验法和访谈法研究小学一至三年级学生解决加减法算术题的策略发展特点，发现：解决两个数的算术题时，不同年级的学生使用出声策略、拆十策略、手势策略、逆算策略、数数策略的次数差异显著，随着年级的增长使用频率逐渐降低;解决三个数的算术题时，各年级学生使用出声策略、手势策略、对位策略的次数差异显著，随着年级的增长使用频率逐渐增高。

（二）学习策略的使用效果

毛秀珍等探讨了小学生数学参与、数学学习策略和数学成绩三者间的关系。他们以“小学生学习参与量表”和“小学生数学学习策略量表”为工具，对398名五年级学生施测。结果显示，三者间两两相关显著，数学参与对数学学习策略和数学成绩有显著影响，数学学习策略在数学参与对数学成绩的影响中起中介作用，数学学习策略对数学成绩有44.5%的贡献。而Patricia等研究发现，学习策略的使用对学生一个学期前、后两个阶段的学习成绩有显著影响。

表征策略在数学问题解决过程中起着非常重要的作用，学生会表现出不同的问题表征方式。董妍等以124名六年级学生为被试，采用应用题解决问卷考察小学生应用题表征的类型与特点。结果发现，小学生应用题的表征方式包括复述内容、图式表征、图片表征、直译表征、语义结构分析等，其中图式表征和语义结构分析是使用次数最多的;而且，成功的解题者在图式表征、直译表征和语义结构分析表征下的成绩显著优于不成功的解题者。而Van Garderen等研究发现，优生使用图式表征策略显著多于差生和一般学生，一般学生与差生之间无显著差异;正确解决问题的学生更经常使用图式表征策略。

概念图是一个用图示表征知识的工具。对学生而言，绘制概念图是一种有效的学习策略，可以作为一种选择性注意策略、记忆策略、组织策略、精加工策略、元认知策略等。概念图对不同先前知识水平学生影响的研究表明，对于先前知识水平较低的学生，概念图策略的影响效果更好，即有利于成绩较差的学生提高学习成绩。

计算内容在小学数学学习中占有很大的比重。不管是数学规律的发现或数学现象的探究，还是数学问题的解决，都离不开计算。掌握计算策略能更好地促进小学生的数学学习。何伟等分析了小学生运算错误类型，结果显示，小学生在整数乘法、整数除法、整数混合运算、小数加法、小数减法和小数混合运算等六个方面出现错误的类型主要为概念性错误，而出现概念性错误的原因主要包括复杂运算中算法与算理的理解问题、位值的理解问题和混合运算中运算规则的理解问题。为了使计算简便、快速，学生会采用一些简算策略。简算是指综合运用算理来简化复杂计算，学生只有理清算理，才能正确、快速地完成计算。

学习不良儿童在学习策略方面主要表现出如下几个特征：（1）策略数量和储备不足。相对于一般儿童，学习不良儿童的策略数量和储备明显不足，且缺乏策略是其学习困难的主要原因之一。（2）策略选择和运用水平不高。学习不良儿童常常根本不使用策略，或很少使用其他策略，更多地运用容易导致错误的直译策略，因而使得信息加工低效、学习成绩不佳。（3）策略选择和运用适应性差。学习不良儿童往往不主动且不灵活，不能根据任务的需求选择和运用有效的策略。在完成记忆任务时，学习不良儿童多半采取被动、僵化的复述策略。（4）策略執行效能低下。学习不良儿童更多地表现为一种利用缺失，即虽然与一般儿童同样地运用了策略，但执行效能低下，从中受益更少。（5）策略发展上的“固着”效应。一般儿童在年幼时往往也会选择和运用较为低级的策略，但随着年龄的发展，其策略选择和运用水平会有明显提高;而学习不良儿童不仅选择和运用较为低级的策略，而且不能随着年龄的发展而改善，表现出一种低级策略的“固着”效应。

（三）数学学习策略的训练干预

数学学习策略既包括一般的学习策略，如识记策略、加工策略、组织策略等，也包括数学学习的特有策略，如以简驭繁、进退互用、数形迁移、化生为熟、正难则反、倒顺互通、动静转换、分合相辅、以美启真等。数学学习策略的训练干预就是采用一定的方式训练学生掌握数学学习策略，以提高学习效益。

方平等研究发现，随堂渗透数学学习策略的方式对训练效果有显著影响;出声思维训练能使学生及时发现自己使用的策略同试验者讲授的策略之间的差异，有助于学生对策略的掌握;训练时间对训练效果有影響，一般训练时间宜长。

张履祥等编制了《学习策略训练》教材（包括课堂学习策略、巩固记忆策略、解题思维策略、创造学习策略和总结考试策略等六个单元），由此对小学四年级学生开展每单元六课时的训练，发现效果十分明显。

蒋世雷等依据《小学数学学习策略》教材，对小学六年级学生分别开展概念学习策略、计算学习策略、几何知识学习策略和应用题解题策略等四大块学习策略的系统训练。对于每一种策略，教学步骤如下：（1）趣味引入，揭示课题;（2）讲解策略的意义;（3）通过具体实例讲解策略的运用及其范围和条件;（4）通过练习体会并运用策略;（5）反思总结。结果显示，实验班的平均成绩显著高于对照班。

郭成采用元认知内隐训练、元认知外显训练和一般思维策略训练等三种方式对小学五年级学生开展解题思维训练。元认知内隐训练强调让学生在教师示范的过程中自己体会、感受元认知策略的有效性。比如，教师在例题的讲解过程中，自然地展示自己对解题过程的元认知监控，而不特意地以一些明显的外在操作来要求和指导学生。元认知外显训练强调教师以一些明显的外在操作来要求和指导学生怎样学习、怎样掌握。其操作程序可以是：（1）结合例题向学生讲解元认知方面的知识;（2）以展示元认知监控的教学思路讲解应用题的解题策略，并告诉学生这种策略的使用对成功解决应用题的有效性;（3）设计并使用专门的“元认知监控单”让学生完成提示性练习;（4）要求学生运用出声思维（说理由）大声地自我指导，监控思维活动。一般思维策略训练的主要思想是直接告诉学生这些策略的含义并力图让学生记忆这些策略。

窦菲菲等对小学五年级学生开展画图表征策略训练，探讨元认知在画图表征策略和数学问题解决中的作用。结果显示，策略学习后小学生数学问题解决的成绩显著高于策略学习前，元认知在画图表征策略对数学问题解决的影响关系中起中介作用。

汤服成等以261名小学四至六年级学生为被试开展实验研究。实验班采取数学元认知监控学习策略训练：（1）指导学生制订可行的学习目标和学习计划;（2）用“大声思维法”展现数学学习的思维过程，示范自我监测与评价;（3）引导学生自觉对数学学习过程做出反思、补救和总结;（4）加强元认知监控学习策略培养过程中的主体体验，即让学生通过尝试、应用获得关于具体策略的情感、态度、价值等方面的内心认同。结果表明，数学元认知监控学习策略训练对数学成绩起到了较明显的促进作用。

二、对小学数学教学的启示

（一）选择性注意策略的培养

选择性注意策略是指在学习情境中将注意集中于重要信息的学习策略。教学中，教师要有针对性地对学生开展选择性注意策略的培养。

首先，教给学生专注于重要信息的策略。（1）画线或标着重号。在重要文字下面画线或标着重号，以增强对重要信息的敏感性。（2）写摘录、摘要、列标题。摘录是摘抄学习材料中的原句，摘要是用自己的话概括学习材料的主要内容，标题是对学习材料中心内容的进一步概括。（3）做笔记。养成边听课边做笔记的习惯，即经过自己的辨认和选择，记录老师讲课中的一些重要信息。

其次，引导学生分析问题中的重要信息。问题中总有重要信息、相关信息、无关信息，解决问题时需要有效地识别重要信息，选择相关信息，排除无关信息的干扰，才能正确地表征问题。

例1同学们在环形跑道上跑步，小亚跑了200米，小胖比小亚多跑10米，小丁比小胖少跑3米，小胖每分钟跑360米，小丁跑了多少米？

教学本题时，要引导学生在重要的文字下面画线，并分析题目中的信息，包括重要信息、相关信息和无关信息。具体来说，可以在“小亚跑了200米，小胖比小亚多跑10米，小丁比小胖少跑3米，小丁跑了多少米？”下面画线，进一步分析得出两个重要信息：（1）小丁比小胖少跑3米;（2）小丁跑了多少米？两个相关信息：（1）小亚跑了200米;（2）小胖比小亚多跑10米。两个无关信息：（1）同学们在环形跑道上跑步;（2）小胖每分钟跑360米。

（二）精加工策略的培养

精加工是指当前所学知识与已有知识建立联系或对新知识进行拓展的过程。精加工策略主要包括画图、类比、拓展等具体方式。

1.画图策略。

小学生的思维以形象思维为主，他们常用图画和符号记录的方式描述其解决问题的步骤。画图能直观显示题意，有条理地表示数量，从而帮助学生发现数量之间的关系，形成解题的思路。心理学的研究也表明，画图作为一种问题表征策略，能够促进小学生数学问题的解决。最常见的图形是示意图，即把文字、符号等表达的信息用直观的图形表示出来。

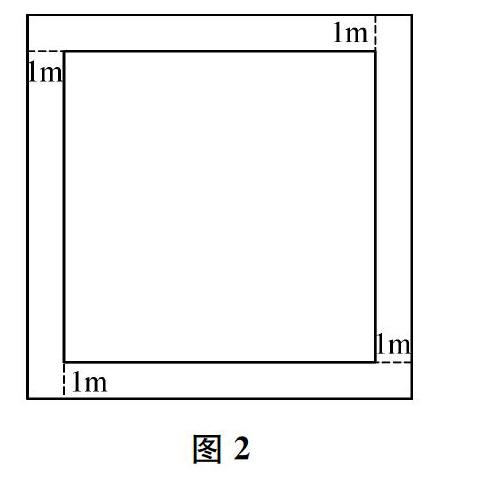
例2有一个正方形草坪，沿草坪四周向外修建1米宽的小路，路的面积是80平方米，求草坪的面积。

解答此题时，教师可以鼓励学生画示意图。学生若能画出图1或图2，将十分有助于问题的解决。

此外，作为一种促进意义学习的有效策略，绘制概念图有利于学生从整体上把握数学知识，建立系统完整的知识框架，完善认知结构。教学中，教师可给出某一课题的半结构式概念图，提供概念列表和连接词，让学生自己选择相应的要素形成完整的概念图。

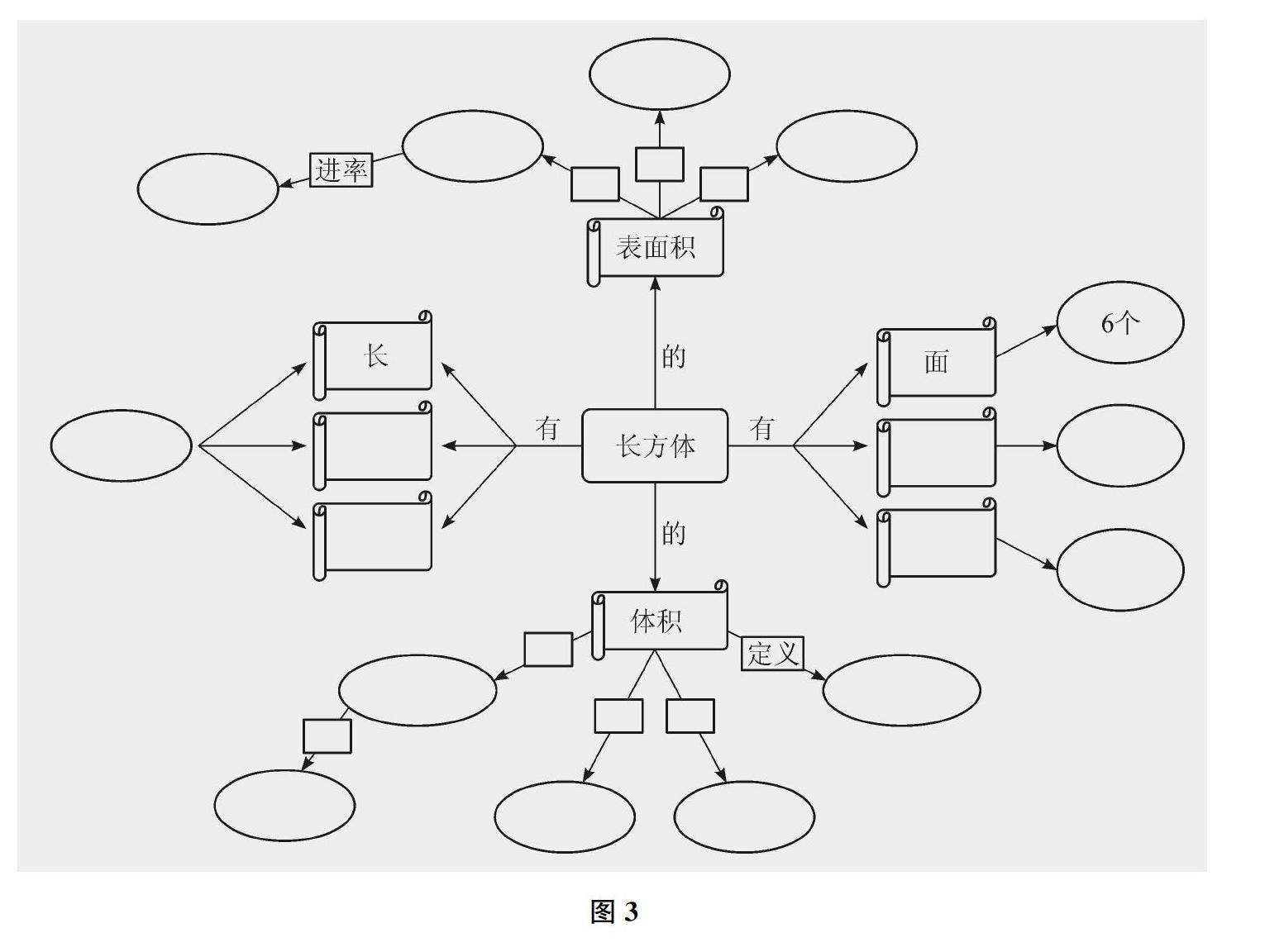
例如，教学“长方体”一章的内容后，可以出示有空缺的概念图（如图3），给出如下条件：宽、棱、高、顶点、8个、12条、单位、公式、进率、定义、S=（ab+ah+bh）×2、V=abh、V=sh、相交于一个顶点的三条棱、长方体6个面的总面积、物体所占空间的大小、平方米、平方分米、平方厘米、立方米、立方分米、立方厘米、相邻单位之间进率是1000、相邻单位之间进率是100。然后，让学生用给出的条件（可重复使用）填补概念图中的空缺。

2.类比策略。

类比是根据两类对象之间在某些属性上的相同或相似所做的一种类推。运用类比，可以将抽象的内容具体化、形象化，陌生的知识转化为熟悉的知识，深奥难懂的道理简单明了地揭示出来。教学中，教师要善于运用类比策略引导学生从已知过渡到未知、从近过渡到远等。运用类比策略时，必须做到以下几点：（1）考虑可比性，所选的比方与类比的事物必须具有某种同一性和相似性;（2）考虑可接受性，所选的比方必须是学生熟悉、易懂的;（3）比方是手段，不是目的，只能起过渡作用，不能喧宾夺主;（4）注意紧扣重点、难点。

例3一旅游小队去爬山，上午8时上山，每小时平均行3千米，到达山顶休息1小时，下山时每小时平均行5千米，下午2时到达山底。全程共行了19千米。上山和下山的路程各是多少千米？

本题表面上是一个行程问题，实质上是一个典型的“鸡兔同笼”问题。因为其特征是：（1）已知两种事物的单值，即上山速度为3千米/小时、下山速度为5千米/小时，相当于每只鸡2只脚、每

图3只兔4只脚。（2）已知这两种事物的总个数，即共行了5小时、19千米，相当于鸡、兔共有35个头（35只）、94只脚。（3）要求这两种事物的个数，即上山、下山的时间（路程）各是多少小时（千米），相当于鸡、兔各有多少只（只脚）。

因此，教学中，可以运用类比策略，引导学生联想“鸡兔同笼”问题的解答方法得到本题的解答方法。如假设法：假设5小时都是上山时间，则共行路程为3×5=15（千米），比实际少行了19-15=4（千米），原因是把下山时间当作了上山时间，则下山时间为4÷（5-3）=2（小时），故下山路程是5×2=10（千米），上山路程是19-10=9（千米）。当然，也可以假设5小时都是下山时间。

3.拓展策略。

对知识加以拓展是深化理解知识的重要途径。对小学数学知识做拓展研究，可以拓宽小学生的知识面，在有效加深小学生对数学知识理解的基础上，还能与其他学科的知识联系起来。教学中，可以从数学文化、数学知识、数学方法、数学问题等方面拓展。

例如，教学《圆的周长》一课时，教师可以拓展介绍圆周率的历史：从阿基米德发现了“当正多边形的边数增加时，它的形状逐渐接近圆”，刘徽提出了“割圆术”，到祖冲之刻苦钻研，用竹片做的筹码反复演算，将圆周率精确到小数点后的七位，也就是3.1415926到3.1415927之间。通过一个个真实生动的故事，可以拉近学生与数学家之间的距离，让学生感受数学家的探索精神与数学知识的源远流长，激发学生的学习兴趣。

例4小明和小兰在周长为400米的环形跑道上跑步，小明每秒钟跑5米，小兰每秒钟跑3米，他们从同一地点同时出发，反向而跑，那么，二人从出发到第一次相遇需要多长时间？

拓展题小明和小兰在周长为400米的环形跑道上跑步，小明每秒钟跑5米，小兰每秒钟跑3米，他们从同一地点同时出发，反向而跑，那么，二人从出发到第二次相遇需要多长时间？

这里，拓展题是例题的变形，要求算出第二次相遇的时间（还可以要求算出第n次相遇的时间），目的是让学生理解相遇问题的实质，总结出：无论相遇问题的变化有多复杂，只要找出速度、总路程的信息，就可以运用“总路程÷速度和=相遇时间”这一规律解决问题。

（三）元认知策略的培养

元认知提问能够引发学生的计划、监控和评价等元认知加工过程，促使学生思考认知活动的特点、策略和当前遇到的困难，并决定是否调整以及如何调整等。元认知提问能使学生对自己的学习活动形成清晰的意识，强化元认知策略，促进数学学习。解题教学中，教师可引导学生使用以下四类问题开展元认知自我提问。

教育研究与评论小学教育教学/2021年第2期前沿论坛理解问题。帮助学生理解问题中的信息。比如：这个问题的条件是什么？关键的信息有哪些？要完成的任务是什么？是否要分解出子目标？等等。在回答理解问题时，学生必须专注于问题的基本特征，并识别给出的条件、数学术语、提出的问题以及要实施的数学过程。

联系问题。帮助学生理解问题更深层次的关系结构。比如：这个问题与之前接触的哪些问题有联系？与以前接触的问题有什么不同？有什么相似？等等。在回答联系问题时，学生必须专注于先前的知识，并定义问题的结构特征和提供的信息。

策略问题。促使学生计划和选择合适的解题策略。比如：解決这个问题的策略是什么？为什么可以运用这种策略来解决问题？等等。在回答策略问题时，学生需要描述他们选择了什么策略（陈述性知识），如何实施策略（程序性知识），为什么选择的策略适合解决这个问题（条件性知识）。

反思问题。帮助学生监控和评估解决问题的过程。比如：问题解决得正确吗？还有其他解决方法吗？问题可以变式吗？等等。在回答反思问题时，学生需要从不同的角度思考他们的解决方法是否有效。

*本文系喻平教授团队的“数学学习心理学研究及其教学启示”（小学）系列文章之六。

参考文献：

[1] J.H.Flavell.Cognitive Development[M].Englewood Cliffs， New Jersey：PrenticeHall Ine.，1985.

[2] 庞虹.小学儿童记忆中组织策略发展的实验研究[J].心理学报，1992（4）.

[3] 何进军，刘华山.10～14岁优差生的认知策略及发展研究[J].心理科学，1996（3）.

[4] 刘电芝，黄希庭.小学生数学学习策略的运用与发展特点[J].心理科学，2005（2）.

[5] 陈英和， 耿柳娜. 小学一～三年级儿童加减法策略选择的发展特点研究[J].心理发展与教育，2005（2）.

[6] 毛秀珍，王娅婷，韦嘉.小学生“数学参与”“数学学习策略”和“数学成绩”间的关系研究[J].数学教育学报，2017（6）.

[7]Pokay Patricia，Blumenfeld Phyllis C..Predicting achievement early and late in the semester：The role of motivation and use of learning strategies[J].Journal of Educational Psychology，1990（1）.

[8] 董妍，路海东，俞国良.小学生应用题表征的类型和特点[J].心理科学，2004（6）.

[9] Delinda Van Garderen，Marjorie Montague.VisualSpatial Representation， Mathematical Problem Solving，and Students of Varying Abilities[J].Learning Disabilities Research & Practice，2003（4）.

[10] 王立君，顾海根，吴樟彬.概念图对不同个性差异学生学习促进的实验研究[J].心理科学，2010（2）.

[11] 何伟，董连春，法旭，等.南疆小学生数学运算错误类型及分析——基于新疆大规模测评数据[J].数学教育学报，2020（1）.

[12] 陳英和，赵笑梅.学习不良儿童的策略研究[J].心理科学进展，2005（5）.

[13] 方平，郭春彦，汪玲，等.数学学习策略的实验研究[J].心理发展与教育，2000（1）.

[14] 张履祥，钱含芬.小学生学习策略训练效应的实验研究[J].心理科学，2000（1）.

[15] 蒋世雷，傅玉蓉.《小学数学学习策略》教材实践对学生学会学习数学的影响实验报告[J].西南师范大学学报（人文社会科学版），2005（4）.

[16] 郭成.元认知训练对小学生数学问题解题能力的影响[J].西南师范大学学报（自然科学版），2004（1）.

[17] 窦菲菲，刘志敏，张景焕，等.元认知在画图表征策略和小学生数学问题解决能力中的中介作用[J].心理学探新，2012（2）.

[18] 汤服成，梁宇.小学四～六年级学生数学元认知监控学习策略培养的研究[J].数学教育学报，2008（1）.

[19] 陈旭，刘电芝.学习策略（三）选择性注意学习策略[J].学科教育，1997（3）.