基于仿射变换的地磁匹配定位算法

严羽灵，唐清善，白 创

(长沙理工大学 物理与电子科学学院，湖南 长沙 410114)

地磁场是属于地球的天然资源[1]。大部分动物能够利用地磁场提供的地磁信息进行导航[2-3]。包括鲸鱼、海龟、候鸟在内的迁徙动物[4]受各种气候环境的影响还可测定精确的位置。地磁导航包括地磁场模型[5]建立、地磁场实时测量和地磁导航算法[6]。地磁导航算法可以分为地磁匹配算法[7]和地磁滤波算法。地磁滤波算法虽然实时性强，但是地磁场相对地理位置具有较强的非线性，导致滤波容易发散。地磁匹配算法[8-9]原理简单，且匹配精度较高，在地磁导航中应用较多。

目前比较常见的算法是地磁场等值线匹配(Magnetic Contour Matching，MAGCOM)算法和迭代最近等值线匹配(Iterative Closest Contour Point，ICCP)算法[10]。MAGCOM 算法只能修正位移误差，不能校正角度误差[11]。而 ICCP 算法[12-13]只能修正角度误差和位移误差，不能修正伸缩误差，因此精度不高。本文提出了一种基于仿射变换的地磁匹配定位算法。仿射变换[14-15]比较常见的有旋转、平移、伸缩变换、反射和剪切。由于惯导系统输出的轨迹与真实轨迹之间只存在位移、角度和伸缩误差，所以只考虑前面3种变换。为了实现该算法，本文改进了第12代国际地磁参考场模型，并输出地磁数据库。再通过MATLAB对参考轨迹、真实轨迹以及该算法进行了仿真。然后通过Mathematica中的迭代和数值求解函数解非线性方程组，并将解输入到MATLAB中进行匹配定位，将各组解的匹配效果进行了比较。

1 仿射变换算法原理

1.1 问题描述

惯导系统存在随时间累加的定位误差，导致惯导系统所输出的轨迹与真实轨迹之间存在位移、角度和伸缩误差。该情况可以用如图1所示的轨迹示意图来描述。

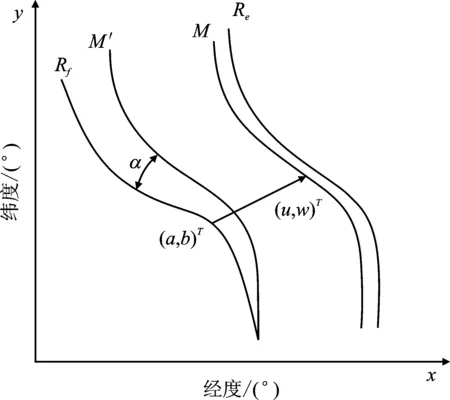
图1 轨迹示意图

其中，曲线Rf表示捷联惯导系统输出的参考轨迹；曲线M是经过仿射变换算法得到的匹配轨迹，其位于真实轨迹Re附近；作曲线M的平行线M′。从图1可以看出匹配轨迹与参考轨迹存在角度误差α。除了角度误差，还存在初始位置误差和伸缩误差，Δx和Δy分别表示初始经度、纬度误差；k1和k2表示经度、纬度方向的伸缩误差。令(a,b)T是参考轨迹上的一点(a表示经度，b表示纬度)，参考轨迹的初始点坐标为(a1,b1)T，那么(a,b)T对应的匹配轨迹上的点是(u,w)T。

1.2 仿射变换模型

仿射变换是二维坐标到二维坐标之间的线性变换，能够保持二维图形的“平直性”和“平行性”，即直线经变换后还是直线，圆弧经变换后还是圆弧，且二维图形之间的相对位置关系不会变。它的变化包括旋转、平移、伸缩、反射和剪切。本文针对惯导系统匹配定位，根据具体问题只考虑前面3种。图2所示为仿射变换-旋转变化图。

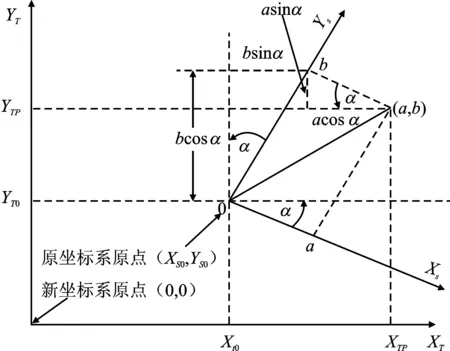
图2 仿射变换-旋转变化图

从图2可知，原始坐标系下的一个点是(a,b)，要对其进行旋转操作。在基于原点的情况下，通过旋转坐标轴就能得到旋转之后的点的坐标，并得到新的坐标系。在这个坐标系中通过立体几何关系确定点(a,b)在新坐标系中的坐标，在新坐标系中它的X、Y坐标分别为(acosα+bsinα)和(bcosα-asinα)。然后在这个位置的基础上加上其在X轴和Y轴的偏移量Δx、Δy。又因点(a,b)只是参考轨迹上的一个点，除了旋转和平移，参考轨迹与匹配轨迹之间还存在伸缩变换关系。由此可以建立如下所示的仿射变换模型

(1)

1.3 地磁匹配

地磁匹配问题可表示为平面上两条曲线的相关性计算，采用平方差(Squared Difference，SD)算法计算曲线之间的相关性，即计算匹配轨迹上各点对应的地磁场特征值与实际测量得到的地磁场特征值之差的平方和。因为该值越小则相差度越小，所以该值达到最小时对应的轨迹序列就是最优的匹配位置。那么SD相关性指标函数表示如下

(2)

式中，I(ui,wi)表示点(ui,wi)T所在位置对应的地磁数据库中地磁特征值；Ir(ai,bi)表示载体在参考点(ai,bi)T时，磁强计实时测量得到的地磁特征值，N表示参考轨迹采样点的总个数。

由于匹配轨迹位于真实轨迹附近，所以匹配结果点所在的地磁特征值约等于对应的真实轨迹上的点的地磁特征值[16]，即存在式(3)。

I(ui,wi)≈Ir(ai,bi)

(3)

为了实现匹配，就要求参考轨迹在匹配轨迹附近，即可将I(ui,wi)在参考点(ai,bi)T处泰勒展开，称I(ui,wi)在点(ai,bi)T的一阶泰勒公式，如式(4)所示。

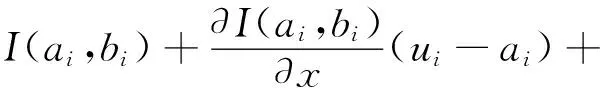
(4)

其中，I(ai,bi)表示在点(ai,bi)T时所对应的地磁数据库中地磁特征值；∂I(ai,bi)/∂x表示地磁特征值对经度方向的梯度在点(ai,bi)T上的取值；∂I(ai,bi)/∂y表示地磁特征值对纬度方向的梯度在点(ai,bi)T上的取值；O2表示的是泰勒展开后所有大于一阶的高阶小项。

联立式(3)和式(4)，并且忽略高阶小项O2,就可得如下式

(5)

将上式简写成如下式

Ix,i(ui-ai)+Iy,i(wi-bi)+It,i≈0

(6)

其中，Ix,i=∂I(ai,bi)/∂x,Iy,i=∂I(ai,bi)/∂y,It,i=∂I(ai,bi)-Ir(ai,bi)。

将式(1)代入式(6)可得

(7)

那么平方差相关性指标函数如下

(8)

其中，a′i=ai-a1；b′i=bi-b1。

因此地磁匹配问题可以转化为求取仿射模型参数Δx、Δy、α、k1、k2的值，以便使得式(8)达到极小值。可以将其对仿射模型参数Δx、Δy、α、k1和k2求一阶偏导数，并使其结果为零，如下所示。

(9)

把式(8)代入式(9)可得如下计算式。

(10)

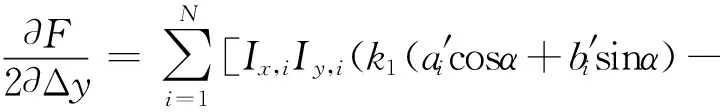
Δy)+Iy,iIt,i]=0

(11)

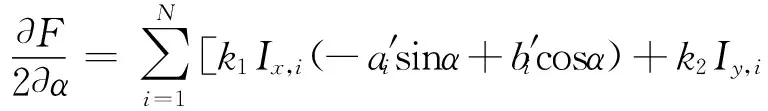
(-a′icosα-b′isinα)]×[Ix,i(k1(a′icosα+b′isinα)-

a′i+Δx)+Iy,i(k2×(-a′isinα+b′icosα)-b′i+Δy)+

It,i]=0

(12)

(13)

(14)

以上5个计算式组成一个以仿射参数Δx、Δy、α、k1和k2为变量的非线性方程组

(15)

因此问题又转化为解非线性方程组(15)，在本文中通过Mathematica对它进行求解，然后将计算所得的5个误差变量Δx、Δy、α、k1和k2代入仿射变换模型式(1)即可得到匹配结果。

2 仿真实验

2.1 地磁数据库的建立

为了建立匹配区域的地磁数据库，本文改进了第12代国际地磁参考场模型。给定经纬度的精度、起始点和终点的经纬度、年份、海拔高度、地点，可以输出起点和终点之间所有点的地磁特征值。地磁特征值包括磁偏角、磁倾角、总磁场强度以及北向、东向、垂直方向的磁场强度。本文选取总磁场强度作为地磁特征值。

2.2 仿射变换算法验证

通过MATLAB模拟参考轨迹和真实轨迹，首先对地磁数据库进行网格化处理，并计算出数据库里面各个点的梯度。然后设定参考轨迹的初始点为(110°,30°)，沿经度和纬度方向的初始速度分别为120 m·s-1和160 m·s-1，每隔50 s取点并给速度加幅值为1 m·s-1粉噪声，再经过双线性插值，将会得到轨迹上各点的经纬度、梯度及相应的点在地磁数据库中检索得到的地磁特征值。最后令真实轨迹的初始点和终点分别为(110°,30°)和(111°,31°)，总速度为200 m·s-1，对其正交分解得到分速度，每隔50 s取点，再使用双线性插值输出轨迹序列点和这些点在库中的地磁特征值，并给地磁特征值加幅值为3 nT的白噪声作为测量值。

将以上相关数据作为输入，通过Mathematica解非线性方程组(15)，采用了两种方法求解：迭代求解和数值求解。表1是关于使用这两种方法计算所得的仿射参数，序号1是迭代法求得的解，序号2～13是数值求解的结果。

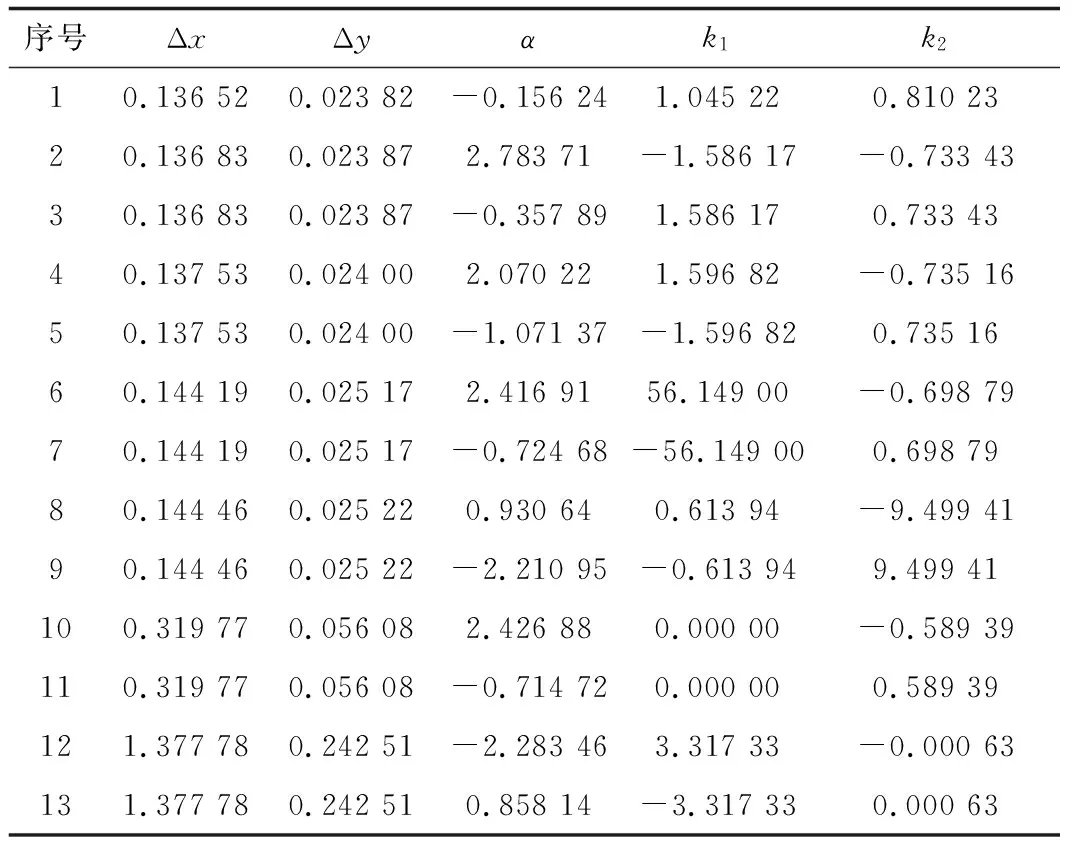
表1 仿射参数

将表1的仿射参数Δx、Δy、α、k1、k2输入到MATLAB中，输出轨迹图和误差图。最终实验结果表明，迭代法所求解的匹配效果最好，图3～图5分别是它的轨迹图、经度误差图和纬度误差图。由图得出，惯导输出参考轨迹的最终定位点与真实轨迹的终点相差6 328.5 m，参考轨迹与真实轨迹之间的经纬度误差分别为-0.034°和0.052°；匹配轨迹的最终的定位点与真实轨迹的终点相差293.3 m，而且匹配轨迹与真实轨迹之间的经纬度误差分别为0.003°、0.000 4°。由此可知，相对于惯导系统，匹配轨迹的定位精度明显提高。

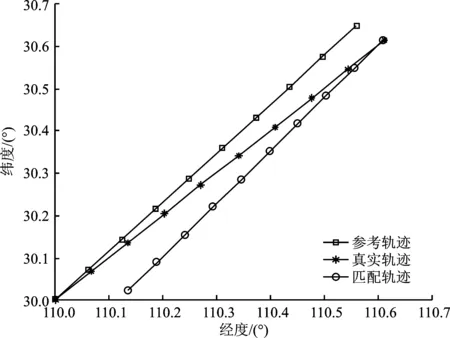
图3 轨迹图

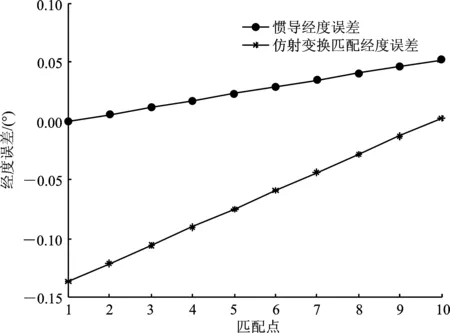
图4 经度误差图

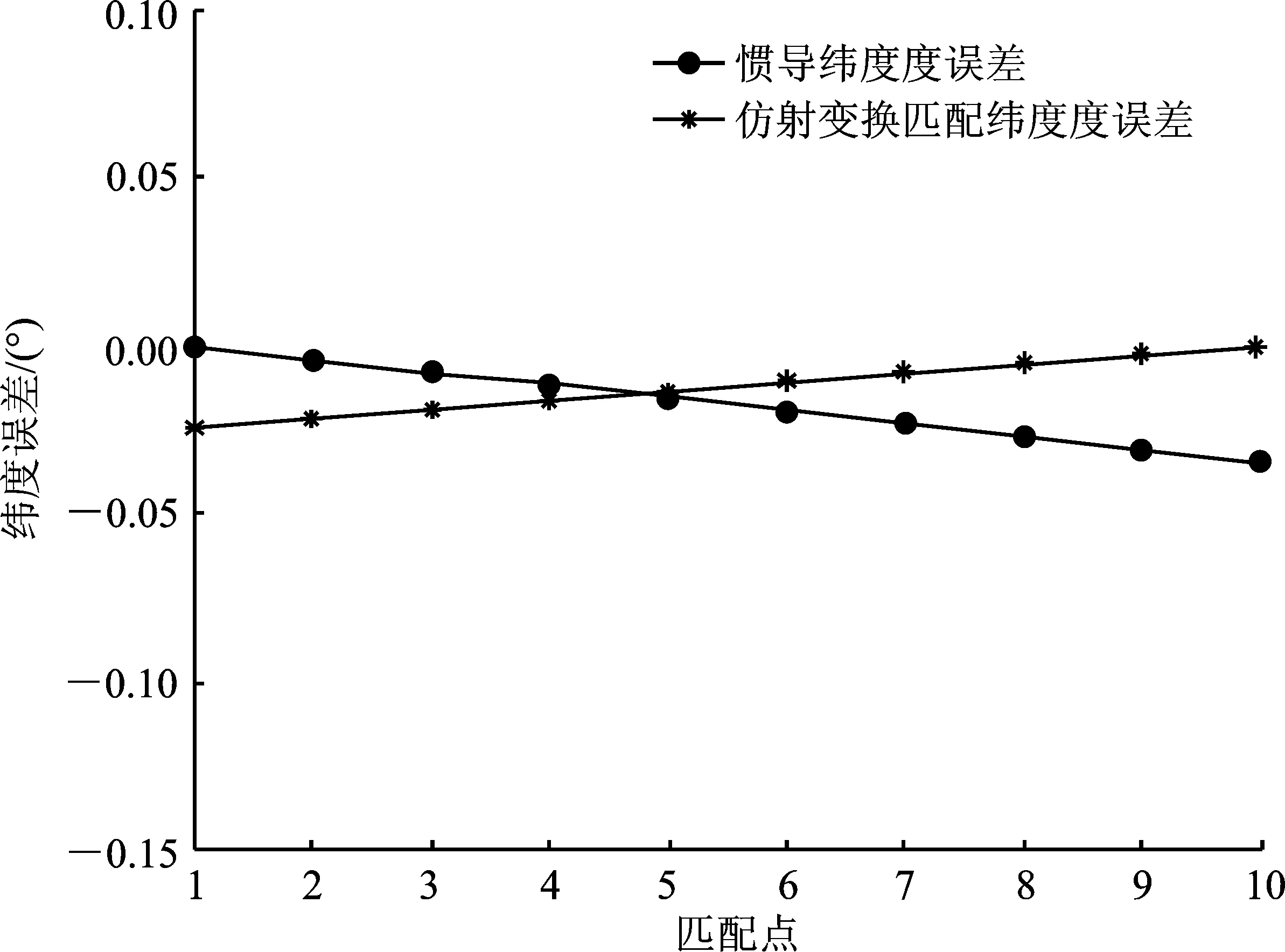
图5 纬度误差图

3 结束语

本文针对惯导系统的定位误差随时间累积的问题，提出了一种基于仿射变换的地磁匹配定位算法。该算法将地磁匹配问题表示为平面上两条曲线的相关性计算，采用了SD算法计算曲线之间的相关性，即计算匹配轨迹上各点对应的地磁场特征值与真实测量得到的地磁场特征值之差的平方和。依据相关性准则，该值达到最小时，其对应的轨迹序列就是最优的匹配位置。实验表明，匹配轨迹的最终定位点与真实轨迹终点相比误差较小，为惯导系统输出的轨迹误差的4.63%。因此本文提出的基于仿射变换的地磁匹配定位算法可以有效修正惯导系统的初始位置误差、初始航向误差和初始速度误差，实现精准的匹配定位。