基于一维WConv-BiLSTM的轴承故障诊断算法
闫书豪,乔美英,2
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000;2.煤炭安全生产河南省协同创新中心,河南 焦作 454000)
现代电气设备多趋向于复杂化与系统化。滚动轴承是电机等旋转电气设备的核心部件,具有易损坏的缺点。滚动轴承发生故障的影响范围较大,会带来巨大损失。因此,轴承的故障诊断对于电气设备的安全运行起着至关重要的作用。在实际工业应用中,电机设备常在变工况的状态下运行,现场传感器所采集多是含噪声干扰的非平稳数据。在噪声干扰的状况下,稳定高效地进行电机轴承故障诊断是目前研究的重点问题[1-2]。
目前,针对含有噪声干扰的轴承故障诊断问题主要集中于信号特征提取与机器学习相结合方法的研究。研究人员通过小波变换[3]、经验模态分解[4]、变分模态分解[5]等信号特征提取方法反映轴承状态。且对工况与噪声干扰不敏感的特征,再通过神经网络[6]、支持向量机[7]等机器学习方法实现故障识别。上述方法在处理小样本低噪声干扰的问题展现出良好的性能,但在处理大量样本且干扰复杂的问题时存在以下问题:将故障诊断方法分为去噪、特征提取、特征降维和特征分类4个孤立的部分,破坏了各部分间的耦合关系,造成部分故障信息损失。因此,采用传统机器学习的算法难以处理数据量较大的问题[8]。
深度学习算法中,卷积神经网络(Convolutional Neural Network,CNN)能有效地提取数据的空间特征,故被广泛应用于图像处理、语音识别、视频处理以及故障诊断等领域[9-10]。在轴承故障诊断领域,基于CNN故障诊断模型的输入通常采用二维的时频图[11]或一维的时序数据[12-13]。李恒等人[14]提出基于短时傅里叶变换(Short-Time Fourier Transform,STFT)和深度全卷积神经网络的轴承故障诊断方法。该方法通过STFT提取时频图特征,利用DCNN实现了端到端的故障诊断。轴承振动数据是一种时间序列数据,在特征提取时使用以上方法,仅提取了数据的空间特性,忽略了时序特性。因此,使用以上方法在处理强噪声干扰的故障诊断问题时所展现出的性能有所下降。
双向长短记忆神经网络(Bidirectional Long and Short Memory,BiLSTM)是循环神经网络的一种特殊结构,其适用于处理序列数据,被广泛应用于语音识别、情感识别等序列数据的处理与预测中[15-16]。BiLSTM网络能有效分析时间序列数据的序列相关性,充分利用数据的时间特征来提高模型的识别效果。但对于数据量较大的问题,其提取数据非线性特征的效果较差,且模型的训练速度较慢,需要与特征提取以及特征降维方法联合使用[17]。
为了解决上述问题,本文提出了一种基于首层为宽卷积核的卷积层(Wide Convolution,WConv)和双向长短记忆神经网络的模型。该模型首先通过短时傅里叶变换,将时域数据转换为时频图;然后通过三层堆叠的一维卷积池化层,提取数据的空间特征并起到保留序列特征的作用,其首层采用宽卷积核以增强网络的感受野;随后通过BiLSTM层提取序列特征;最后经两层全连接层分类。为提高模型处理含噪声干扰的轴承故障诊断问题的性能以及泛化能力,采用mini-batch、批量标准化(Batch Normalization,BN)和数据增强(Data Enhanncement,EM)的方法。文中采用凯西西储大学(Casey Western Reserve University,CWRU)轴承故障数据集构造的噪声干扰数据集对所提出模型的效果进行验证。
1 短时傅里叶变换
短时傅里叶变换是一种时频变换方法,可将时域数据转换为时频图。STFT的定义是采用固定宽度的傅里叶窗函数沿信号的时间轴移动截取信号,将信号截取为多个等长的子信号,每个子信号近似平稳;然后对子信号傅里叶变换,得到各时刻t的局部频谱集合,从而构成时间和频率的二维时频图。其计算式为
(1)
式中,X(t)为原信号;F(t-τ)表示中心位于τ时刻的傅里叶窗。根据文献[14]可知,对于STFT,所选取的傅里叶窗的宽度影响所构造的时频图的时域与频域的分辨率R,而R又决定了时频图所包含的信息。这些信息既包括有用的故障信息,也包含噪声干扰。因此合理的T和F能够使故障信号显著,减少噪声干扰。
(2)
针对轴承振动信号,可以利用轴承故障特征频率的一倍频确定样本的长度,根据二倍频确定STFT窗口的宽度。
2 WConv-LSTM
卷积神经网络是一种前馈神经网络,能高效地提取样本的时空特征。CNN的结构主要包括卷积层、池化层、批量标准化层以及激活层。双向长短记忆神经网络是一种特殊的循环神经网络,能提取数据的时间特征。本文分别利用CNN和LSTM提取时频图的空间特征和序列特征。
2.1 一维卷积层
卷积神经网络可根据处理数据维度建立不同的卷积层。2D卷积应用于图像数据,是通过2D滤波器沿2D 特征图的X和Y两个维度做卷积运算,提取特征图的空间特征,但对于序列数据却很难保留序列特征。1D 卷积适用于一维序列数据,沿数据的单一维度方向移动做卷积运算,在提取空间特征的同时可有效保留序列特征。对于时间序列数据,1D卷积利用多个滤波器沿数据时间轴移动进行卷积运算提取特征,加上偏置后通过一个激活函数就可以得到保留时间特征的特征图,其计算式为
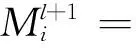
(3)
2.2 池化层
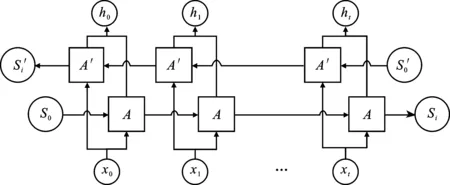
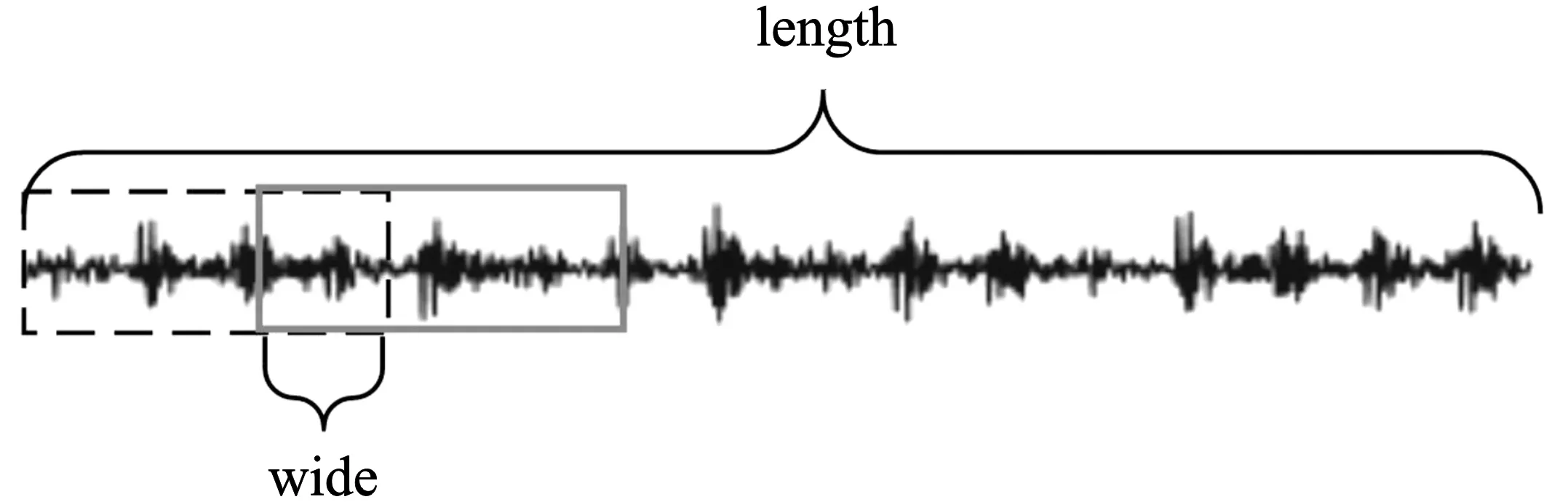
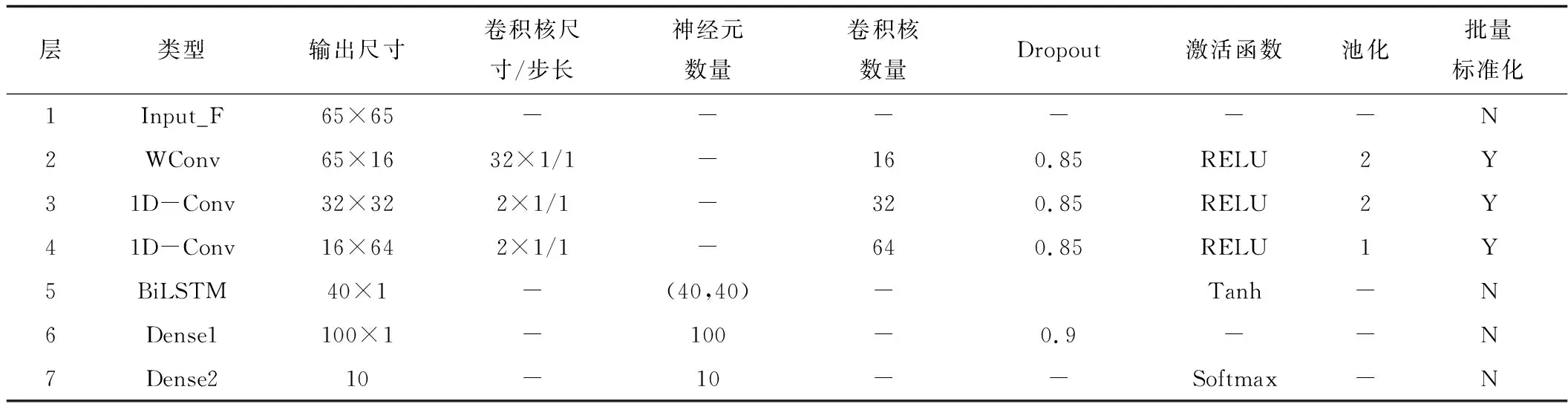
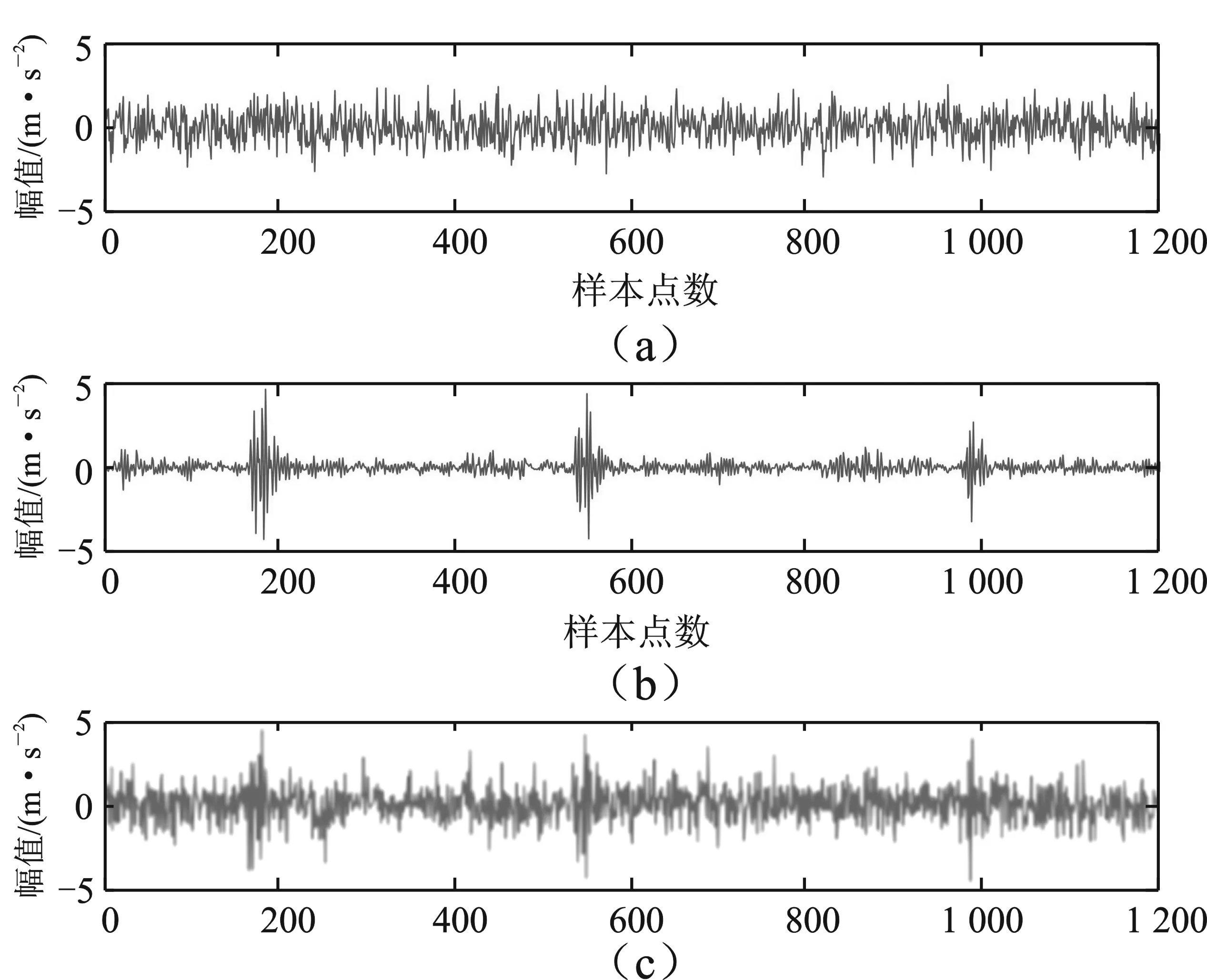
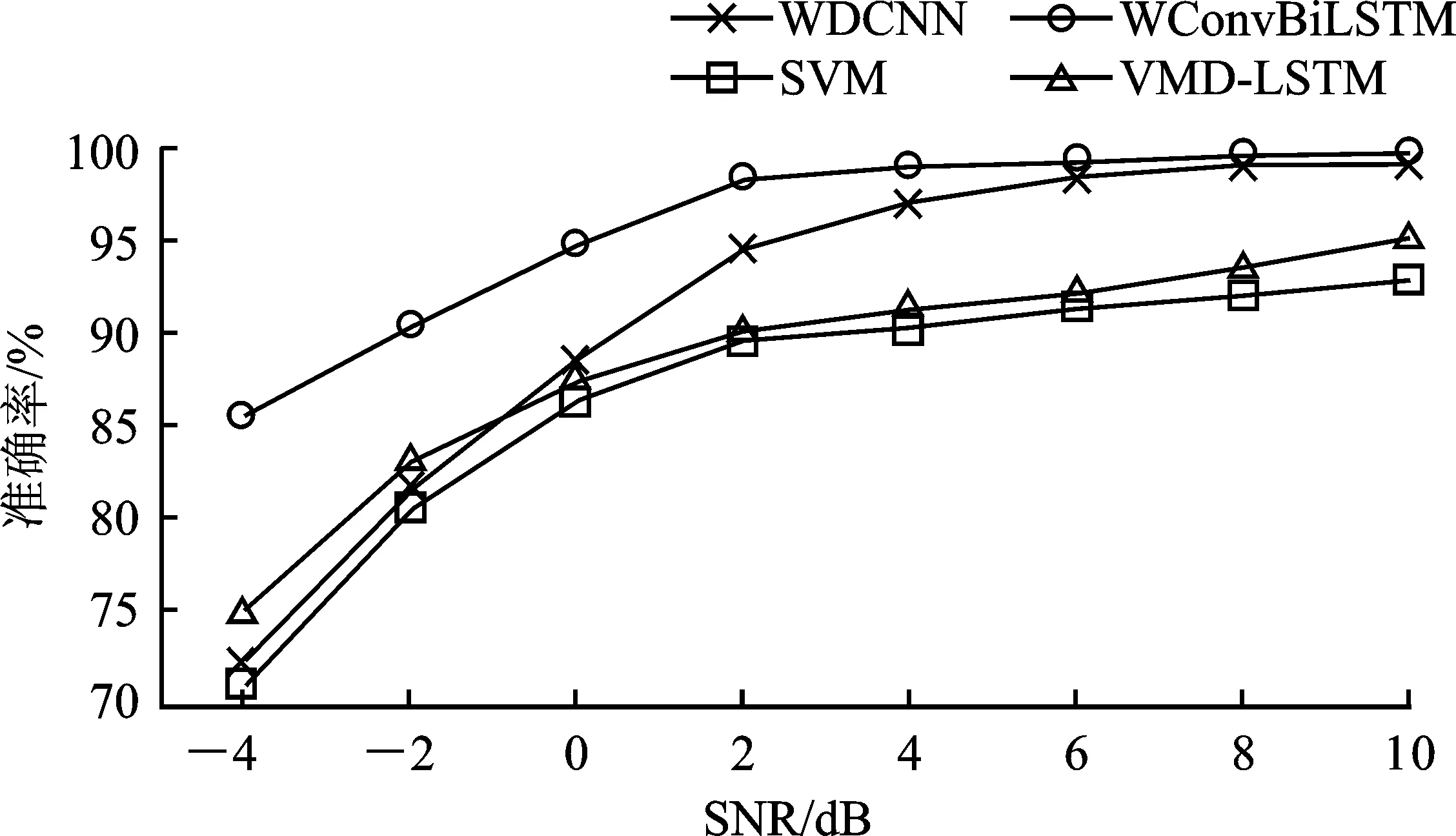
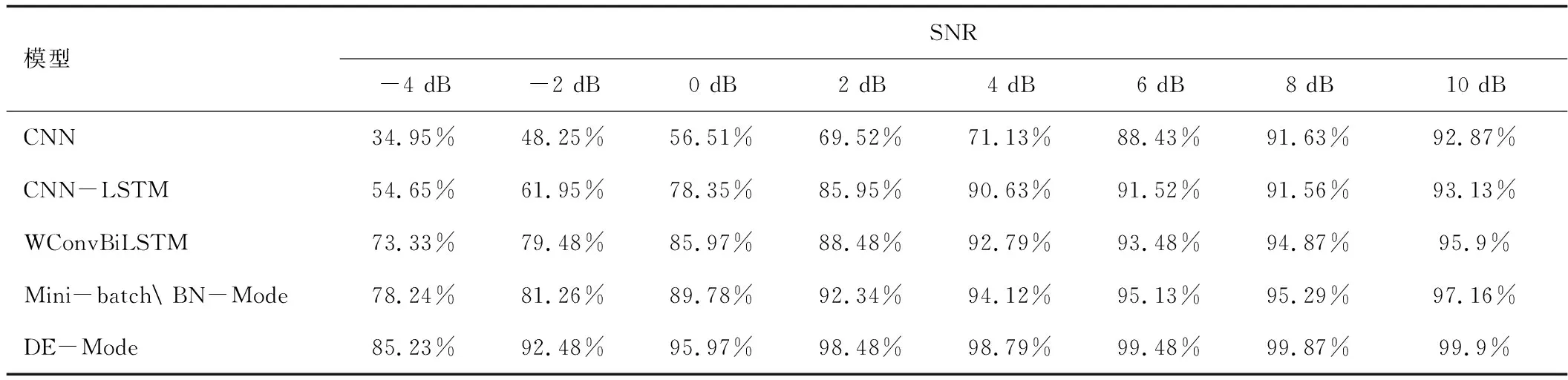
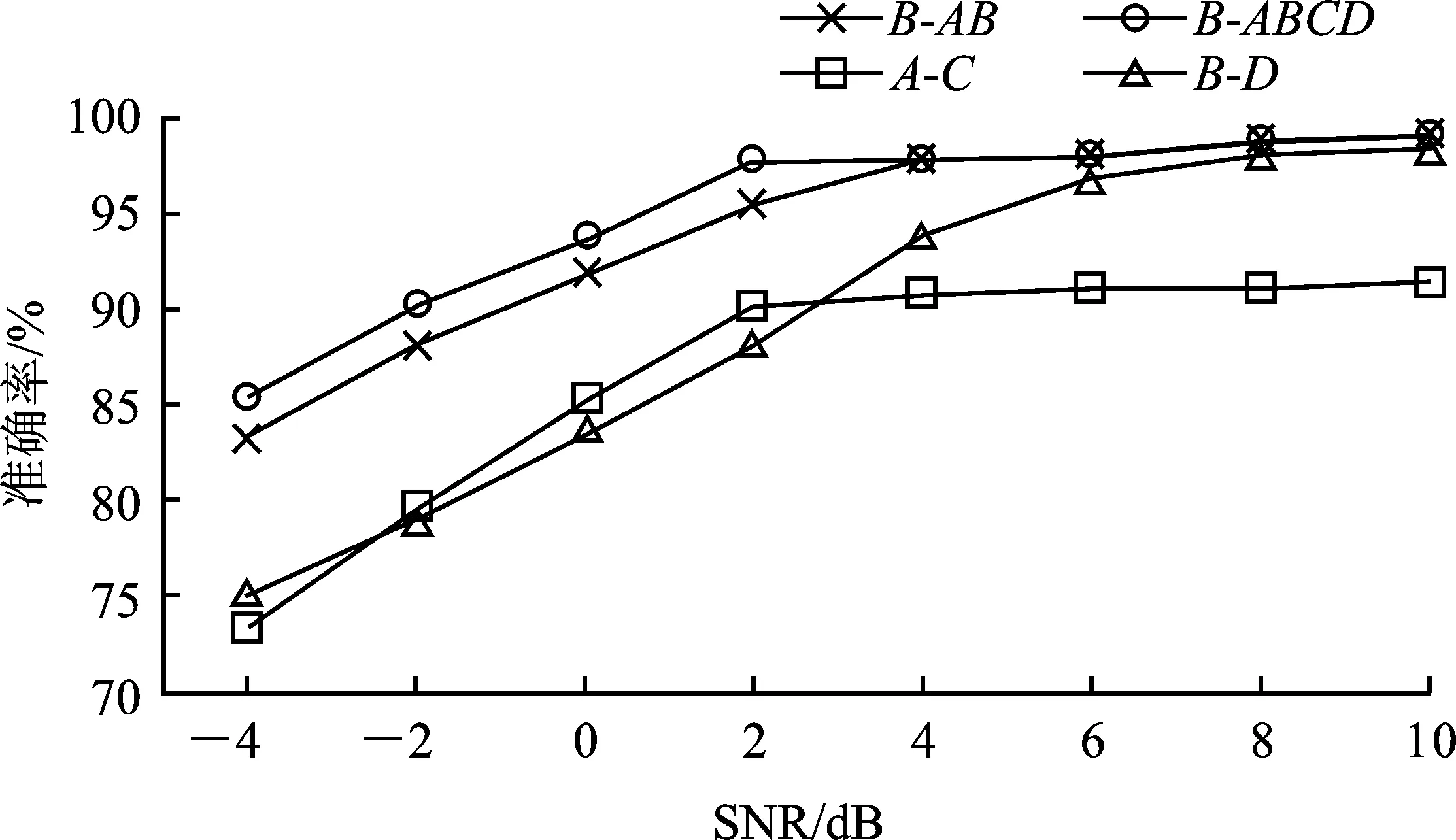
池化层位于卷积层后,对特征图进行下M采样,以降低特征图的维度。本文采用最大池化层,假设卷积层的输出特征图为X∈M,N,D,最大池化层是利用w×d的patch沿特征图的单一方向以步长S移动,将每个特征图Xd划分为多个区域其中1 (4) 批量标准化是为减少内部协方差偏移问题,提出的一种逐层归一化方法,能对神经网络的任意中间层进行归一化操作,并减少各层间样本的差异性,从而起到缩减训练时间以及避免梯度消失和梯度爆炸的作用。在卷积神经网络中,BN层通常设置于卷积层与激活层之间。具体计算式如下 (5) (6) (7) 卷积运算后利用激活函数对特征图进行非线性化处理,以增强模型的非线性表达能力,使学到的特征更具可分性。在CNN网络中常使用Relu作激活函数。Relu函数能有效的解决梯度消失的问题,具体计算式如式(8)所示。 (8) 在全连接层后常利用Softmax函数来处理多分类问题,具体计算式如下 (9) 递归神经网络(Recursive Neural Network,RNN)在处理时间深度较大的问题时,由于隐含层内部结构简单,在进行误差反向传播时会出现的梯度消失或梯度爆炸的问题。LSTM[15]为解决RNN网络误差反向传播时,会出现梯度消失或梯度爆炸的问题,例如将输入门、遗忘门和输出门结构引入,增加了对信息进行长短期选择记忆的功能。所谓的“门”结构就是一个使用sigmoid网络和按位做乘法的操作,之所以被称为“门”是因为sigmoid作为激活函数的神经网络层会输出一个0到1之间的数值,这个数值就代表了当前的输入有多少能通过“门”。 遗忘门的作用是使LSTM网络忘记之前没用的信息。 ft=σ(W[xt,ht-1,Ct-1]+bf) (10) 输入门的作用是根据当前输入[ht-1,xt,bi]和Ct-1共同决定当前时刻的状态Ct。 (11) 输出门会根据当前状态Ct、当前输入xt和上一时刻输出ht-1来决定当前时刻的输出ht。 (12) BiLSTM是LSTM网络的一种特殊形式。如图2所示,相比于传统的LSTM网络只有单向传播的结构,该网络增加了前向传播与后向传播两部分,每个时刻的输出都为该时刻隐层前向输出(fw_output)与后向输出(bw_output)的拼接concat。这种结构充分考虑了数据前后节点之间的相关性,更加适合于处理前后时刻间关联性较强以及呈周期性变化的时间序列数据。 图2 双向循环神经网络拓扑 深度学习算法在训练过程中,常常会出现由训练样本较少引起的过拟合的现象。为解决这种问题,常采用数据增强技术。对于图像数据,常采用对图像进行平移、镜像、旋转等方法来增强数据集。轴承振动信号是一维时间序列数据,本文采用一种重复采样的方法增强数据集,减少过拟合现象。以窗口宽度为w,重复率为wide,步长为s的采样窗沿时间轴重采样,具体过程如图3所示。 图3 数据增强 本文针对轴承振动信号的特点,采用1D 卷积层沿信号的时间轴卷积运算提取特征,保证了在特征提取的同时保留了信号的时间特性,然后采用BiLSTM网络提取进一步提取数据的序列特征。 根据轴承振动信号的特点将CNN与BiLSTM联合使用,具体如图5所示。模型首层WConv1层采用尺寸为(32,1)的宽卷积核,起到增强了网络感受野的作用;WConv层后通过一个池化层来对数据降维;随后通过两个卷积池化层来加深模型的深度,起到增强提取空间特征的作用;然后通过一层BiLSTM层进一步提取数据的序列特征,最后通过两层全连接层(dense)实现分类,激活函数采用softmax。为增强模型的抗干扰性能,分别采用以下方法来提升模型:(1)首层采用宽卷积核的卷积层,增强模型的特征提取效果;(2)通过堆叠的1D卷积池化层提取数据的空间并保留序列特征,通过BiLSTM提取序列特征;(3)通过mini-batch和批量标准化的训练方法,增强模型的泛化能力;(4)通数据增强方法来增强数据集,起到了防止过拟合现象以及增强模型抗噪性的作用。 模型训练过程如图6所示:(1)将原数据划分为训练集与测试集;训练集数据先进行数据增强,然后将时域数据通过STFT转换为时频图。测试集数据先添加不同信噪比的高斯白噪声,构造含噪声干扰的数据,然后通过STFT转换为频谱图;(2)将训练集与测试集分别输入模型,训练集用于训练模型,测试集用于验证模型的抗噪性;(3)经过试验,确定模型的最优结构与最优参数,实现轴承的故障诊断。 试验数据源自凯西西楚大学(CWRU)的模拟轴承故障试验台[17],试验台包括一台2 HP电机、编码器和测功机,试验轴承采用型号为SKF6205的电机轴承。通过电火花技术对测试轴承构造不同点蚀直径的单点故障,并通过加速度传感器采集轴承故障诊断数据。实验数据如表1所示。采用负载为0 HP、1 HP、2 HP和3 HP,损伤部位为内圈、外圈、滚动体和正常的10种不同损伤等级的数据。每种故障类型分别采集800个样本,每1 200个信号点构成一组样本,10种不同等级共8 000组样本。轴承振动信号的时域与频谱图如图7和图8所示。 图8 时频图 试验平台采用Windows10+MATLAB2016b与Ubuntu16.04+Python3.5+Tensorflow11。CPU采用Intel(R)Core(TM)i7-7500U。模型结构的确定采用试验的方法,模型的最优参数如表2所示。 表2 模型详细参数 为验证模型的抗噪性能,通过CWRU数据集构造噪声干扰实验。为原信号添加不同强度的高斯白噪声,以模拟不同信噪比状态下的轴承振动信号。信噪比SNR代表信号与噪声的比例,SNR越小代表信号中所含的噪声比例越大。 (13) 其中,esingal代表信号的能量;enoise代表噪声的能量。如图9所示,原信号添加SNR为-4 dB的噪声后,信号的周期性冲击成分减弱。 图9 SNR为-4 dB时的轴承振动信号图 采用信噪比为-4~10 dB的含噪声信号来验证4种不同模型的抗噪性,结果如图10所示。4种模型在处理低噪声信号时,识别准确率都达到了90%以上。然而在处理强噪声信号时VMD-LSTM模型的抗噪性较差;SVM与CNN模型的抗噪性相对较好,但是对于SNR为-4 dB的信号时,识别准确率也只能达到83%左右。对比以上方法,WConvBiLSTM模型在处理不同噪声强度信号时始终保持较高的识别准确率,说明该模型有良好的抗噪性。 图10 各模型抗噪性对比图 表3为分别采用CNN、CNN-LSTM、WConvBiLSTM,以及为其分别添加Mini-batch/BN和数据增强方法(DE)模型在不同SNR噪声干扰下的对比结果,结果表明本文所提出的WConvBiLSTM模型明显优于其他模型。为其增加Mini-batch/BN和DE方法后,模型的抗噪性有了明显的提升。 表3 不同模型的准确率对比 在实际干扰环境中常常会出现变负载与噪声同时干扰的复杂扰动情况。为验证WConvBiLSTM模型在处理复杂扰动问题时的性能,利用CWRU数据集构建变负载噪声干扰数据集,数据具体如表4所示。 表4 变负载数据集 其中,A-C、B-D代表以A和B负载数据为训练集,C和D负载数据为测试集的情况;B-AB、B-ABCD代表以B负载数为训练集,多种混合负载数据为测试集的情况。 结果如图11所示,模型在处理噪声较小的问题时呈现出的效果较好,准确率都达到了90%以上,最高能达到98%以上。但随着噪声增强,即随着SNR的降低,准确率不断下降。当SNR为-4 dB时部分情况的准确率只能达到75%。总体上,模型针对变负载和噪声干扰的轴承故障诊断问题展现出良好的效果,但是对于噪声强度较大并且存在变负载情况的轴承故障问题的识别准确率还需要进行提高。 图11 不同负载的模型抗噪性对比 本文针对含有噪声干扰的轴承故障诊断问题,并结合轴承振动信号是一种呈周期性的时间序列数据的特点,建立了一种WConvBiLSTM模型。此外本文结合CWRU数据集构造噪声干扰试验,获得了以下结论:(1)首层采用宽卷积核的卷积层,可提高模型的感受野,增强特征提取效果;(2)该模型充分考虑轴承振动信号呈周期性变化的特点,同时利用CNN和BiLSTM网络分别提取数据的空间和序列特征,增强了模型在处理噪声干扰问题时的故障识别精度;(3)采用mini-batch结合BN对模型的训练造成干扰,有效提高了模型的抗噪性。本研究经过大量实验确定了最优模型,并证明WConvBiLSTM模型对工况变化以及噪声干扰问题有较好的鲁棒性。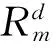
2.3 批量标准化层
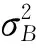
2.4 激活函数
2.5 长短记忆神经网络
2.6 数据增强
3 WCNN-BiLSTM模型结构
4 试验验证
4.1 西楚大学轴承故障诊断数据集

4.2 噪声测试

5 结束语

