基于HAF的混叠多分量LFM信号时域参数测量
吴贞宇,夏厚培
(中国船舶重工集团公司 第七二四研究所,江苏 南京 211106)
现代电子战环境中,雷达信号密度不断增加,雷达体制不断复杂化。电子侦察系统为了更大效率截获信号而在频域宽开[1],使得密集而复杂的雷达信号源源不断地到达雷达接收机,形成时域频域均混叠的混叠脉冲雷达信号。因此,从接收到的混叠脉冲雷达信号中分离出源于不同雷达的信号分量,并进行信号参数测量就显得非常重要[2]。
混叠脉冲雷达信号参数测量方法主要包括时频检测法和参数估计法[3]。时频检测法主要通过分析信号的时频分布特性[4-5],在时频面上实现对混叠信号的分离和参数测量。为了获得较高的时频分辨率,往往采用高次的时频分布,不仅运算量非常大,实时处理困难,而且在信号交叉严重或信噪比不够高时难以测量[6]。不同于时频检测法,参数估计法并不直接对瞬时频率进行测量[7],而是通过估计信号多项式相位的系数来实现混叠信号分离和参数测量[8-9]。
对混叠雷达信号进行参数测量的参数估计法是从最大似然估计发展而来的。最大似然估计是一个多变量的优化过程,计算复杂度非常高。为了提高计算效率,在最大似然估计的基础上提出了高阶模糊函数(High-Order Ambiguity Function,HAF)的方法[10-12]。该方法通过搜索HAF的最大峰值来计算相应的信号相位系数,从而实现信号分离和参数测量。
本文分析了混叠脉冲雷达信号的多项式相位模型,用多项式相位的形式来表示混叠信号。为了处理混叠信号的分离和参数测量问题,介绍了基于HAF的参数估计法。该方法能有效得到混叠信号各分量的相位系数,但对脉冲到达时间、脉宽等时域参数的测量却无能无力。于是本文提出了基于HAF的信号时域参数测量方法,以线性调频(Linear Frequency Modulation,LFM)信号为例进行了详细分析介绍,并进行了仿真实验。实验表明本文提出的方法在HAF测得各信号分量各阶相位系数的基础上也能有效测量信号的时域参数,能完整实现混叠脉冲雷达信号参数测量。
1 混叠LFM信号模型
雷达中所使用的信号相位是时间t的连续函数,根据Stone-Weierstrass理论,在有限观测时间内,任一个时间t的连续函数都可以用一个t的高阶多项式一致逼近。因此,此类信号的相位可以表示成多项式相位的形式,此类信号也被称为多项式相位信号(Polynomial Phase Signal,PPS)[13]。雷达信号也可以用多项式相位的形式来表示[14]。
一个离散单分量的LFM信号的多项式相位形式
(1)
其中,A0为信号幅度;am为m阶相位系数。
实际应用中的混叠脉冲雷达信号可表示为式(2)所示的多分量多项式相位信号(mc-PPS)
(2)
其中,N为混叠信号分量个数;Ak为第k个信号的幅度;ak,m为第k个信号分量的m阶相位系数。
2 基于HAF的参数测量原理
对于信号y(t),其一阶和二阶瞬时矩分别定义为
P1(y(t))=y(t)
(3)
(4)
其中,τ1为时延。
y(t)的高阶瞬时矩可通过迭代的方式表示为
Pm(y(t);τm-1)=Pm-1(t+τm-1;τm-2)·
(5)
信号y(t)的m阶HAF定义为y(t)的m阶瞬时矩Pm(y(t);τm-1)在时间间隔[0,T]上的傅里叶变换,即

(6)
其中,ω∈[-π,π],τ∈(τ1,τ2,…,τm-1);m表示需要计算的HAF阶次。当m=1和m=2时,一阶和二阶瞬时矩的HAF分别为

(7)

(8)
由式(7)和式(8)可以看出,HAF1(y(t),ω,τ)是信号y(t)的傅里叶变换,HAF2(y(t),ω,τ)是信号y(t)的模糊函数。因此,可以将HAFm(y(t),ω,τ)看作信号y(t)的广义模糊函数。
通过定位HAFm(y(t),ω,τ)上的峰值,可按式(9)计算y(t)的相位系数,即
(9)
为简化运算并提高效率,只需要计算某一个延迟τm-1的HAF,即HAFm(y(t),ω,τm-1)。由于ω的范围为-π≤ω≤π,所以相位系数需要满足式(10)。
(10)
采用HAF测量混叠雷达信号参数时,按照信号分量能量强弱的顺序依次检测和分离出各信号分量。图1所示是多个LFM信号分量混叠的HAF2频谱图,其中横坐标为归一化角频率。从图中可以明显看出有一个最高的峰值,对它进行峰值搜索得到其对应的ω值[15],然后带入式(9),即可得到相应的二阶相位系数值。同理可以得到一阶相位系数值,然后将该LFM分量从混叠信号中消去,再重复上述步骤,则可以完成对各信号分量的分离和参数测量。
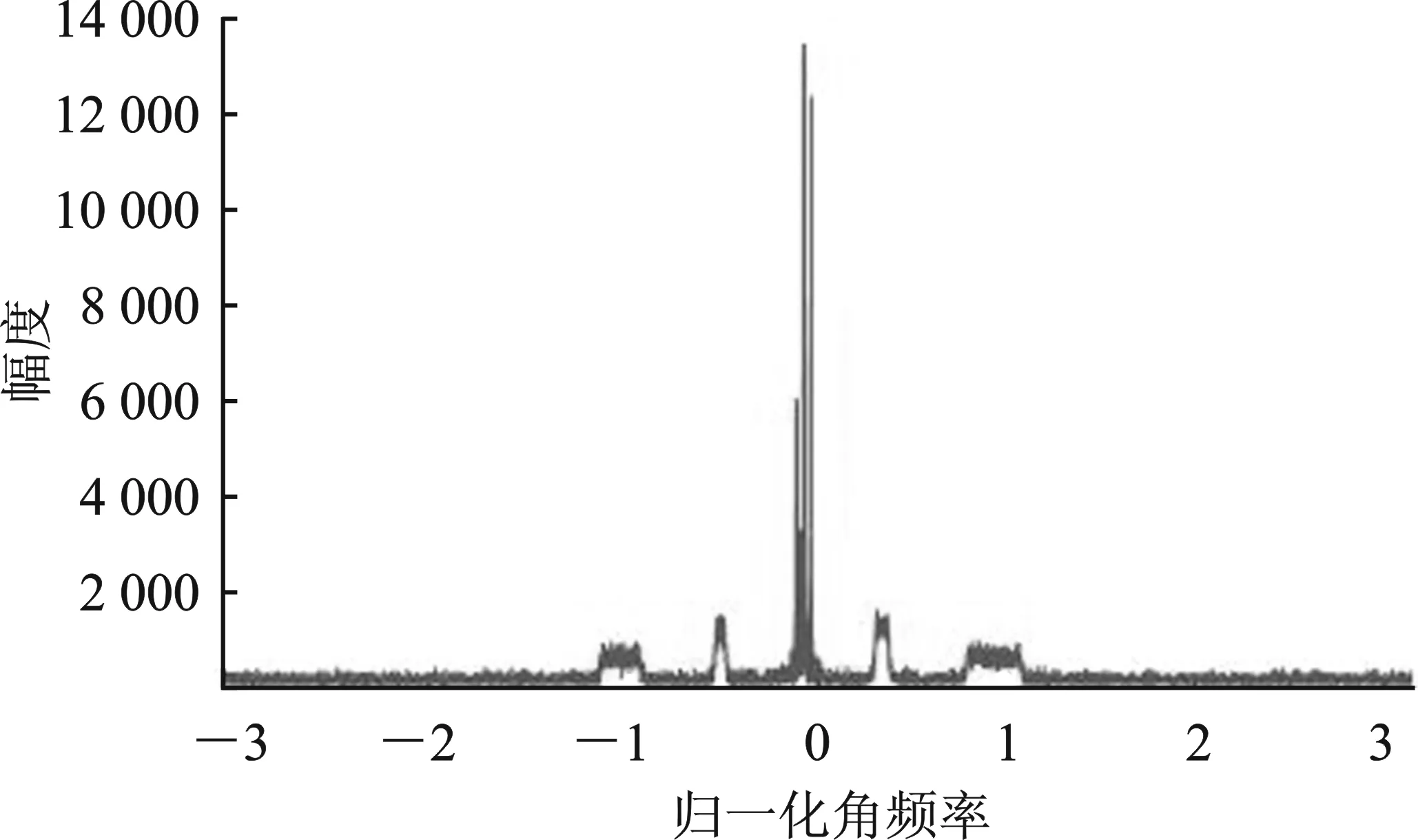
图1 混叠多分量LFM信号的HAF2
3 基于HAF的信号时域参数测量
基于HAF的方法虽然能有效测量混叠信号中各分量的相位系数,且测量结果精度高、计算简单。但由于基于HAF的参数测量方法是对信号的多项式相位形式进行处理得到其相位系数,例如对于混叠LFM信号,虽然使用HAF方法能很方便地得到其各分量的各阶相位系数,但只能由其一阶和二阶相位系数分别得到起始频率和调频斜率等参数,而对于信号的脉冲到达时间、脉冲宽度等时域参数的测量却无能为力。最初在最大似然估计的基础上发展并得出HAF方法时也提到,由于该方法无法确定信号的起始时间,后续只能将HAF应用于处理各信号同时到达同时结束或信号时域参数已知的情况。本文提出一种方法来实现基于HAF的雷达信号时域参数测量。
对于接收到的混叠LFM信号,其多项式相位形式为
(11)
其中,Ak、τk、ak,2、ak,1分别为第k个分量的幅度、脉冲到达时间、二阶相位系数和一阶相位系数;N为分量个数。首先对该混叠信号用上面介绍的HAF方法进行参数检测,可以得到其各分量的各阶相位系数。假设得到的第N个分量的二阶相位系数为a′N,2,对式(11)原始信号进行式(12)所示处理。
(12)
当aN,2≈a′N,2时,式(12)变为式(13)。
y(n)′=
(13)
此时式(13)为一个频率为aN,1-2aN,2τN的单频信号与N-1个新的线性调频信号的混合。其中第k个新的线性调频信号的一次相位系数和二次相位系数分别为ak,1-2k,2τk和ak,2-a′N,2。由式(13)可见,通过处理后,原来很复杂的混叠LFM信号中,第N个信号分量的二阶相位系数被消除,成为了一个简单的单频信号,且得到的单频信号和原始信号中第N个LFM分量的脉冲到达时间和脉冲宽度相同。所以,只要测量该单频信号分量的脉冲到达时间和脉冲宽度,就可以实现对与之相应的原始LFM信号分量的时域参数测量。
单频信号的频谱近似于一个冲击函数,能量集中在很窄的频带内,而LFM信号能量分布在一段很长的频带上。因此可以将上面得到的信号通过一个带通滤波器,滤波器的通带中心为单频信号的频率,这样就可以从单频信号和产生的新线性调频信号中分离出该单频信号,从而实现对单频信号的时域参数测量。
对于分离出来的单频信号,其自相关函数不会快速地衰减,而信号中的噪声是随机性很强的一个序列,相邻点之间是独立分布的,其自相关函数为一个冲激响应,只有在偏移量τ=0时自相关函数才不等于0。为了使本文所提出的方法在低信噪比条件下仍然能够有效测量信号时域参数,此处选择使用移位一点的自相关函数[16]。这样可以最大地抑制噪声并积累信号能量,从而提高测量精度。
对式(13)所得到的信号进行带通滤波,所得单频信号记为s(n),则其移位一点自相关函数为
(14)
此时得到的是一个单频信号的移位一点自相关函数,而噪声的影响已经被削弱很多,只要再选择一个合适的判决门限来确定信号的起始和结束时间,即可实现对单频信号的脉冲到达时间和脉冲宽度的测量。具体处理流程见图2。
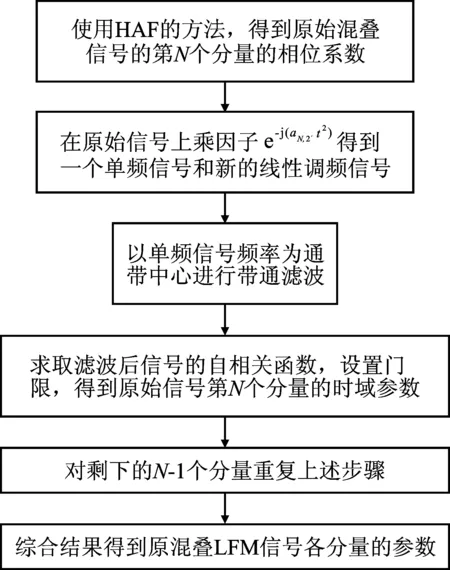
图2 基于HAF的信号时域参数测量流程图
同时,单频信号的频率ωN=aN,1-2aN,2τN,所以aN,1=ωN+2aN,2τN。即此时可由单频信号频率以及原始信号分量的二阶相位系数(aN,2=πkN,kN为调频斜率)以及该分量的脉冲到达时间来得到信号起始频率。将结果与HAF法得到的aN,1(aN,1=2πf0)相比较,可发现测量结果相近。
4 仿真实验
为了验证本文提出的基于HAF的信号时域参数测量方法,采用混叠四分量LFM信号进行仿真实验。各分量具体参数如表1所示,信号采样频率为200 MHz,信噪比为3 dB,采样时间为200 μs。
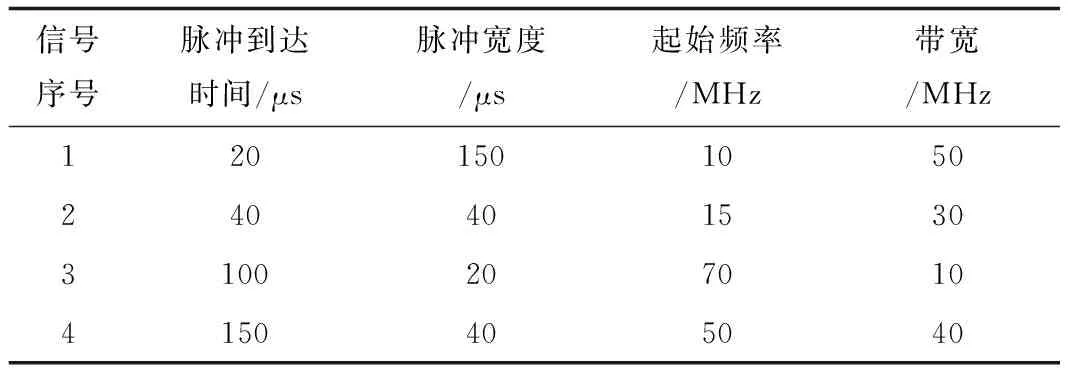
表1 信号参数
图3为混叠信号的时频分布图,展示了信号的时频混叠情况。图4为其时域图,可以发现无法直接分离和测量信号参数。先用HAF的方法测得各信号分量的各阶相位系数,结果如表2所示。

图3 混叠信号时频分布图
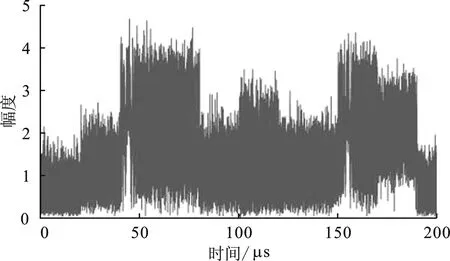
图4 混叠信号时域图
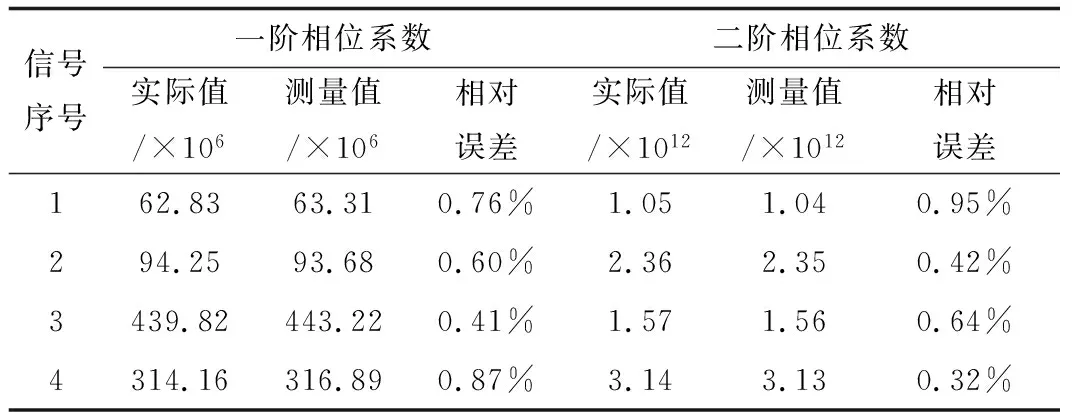
表2 HAF方法所得参数测量结果
HAF的方法只能通过LFM分量的一阶、二阶相位系数分别得到起始频率和调频斜率,对于时域参数则需要本文提出的方法才能得到。
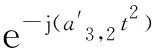
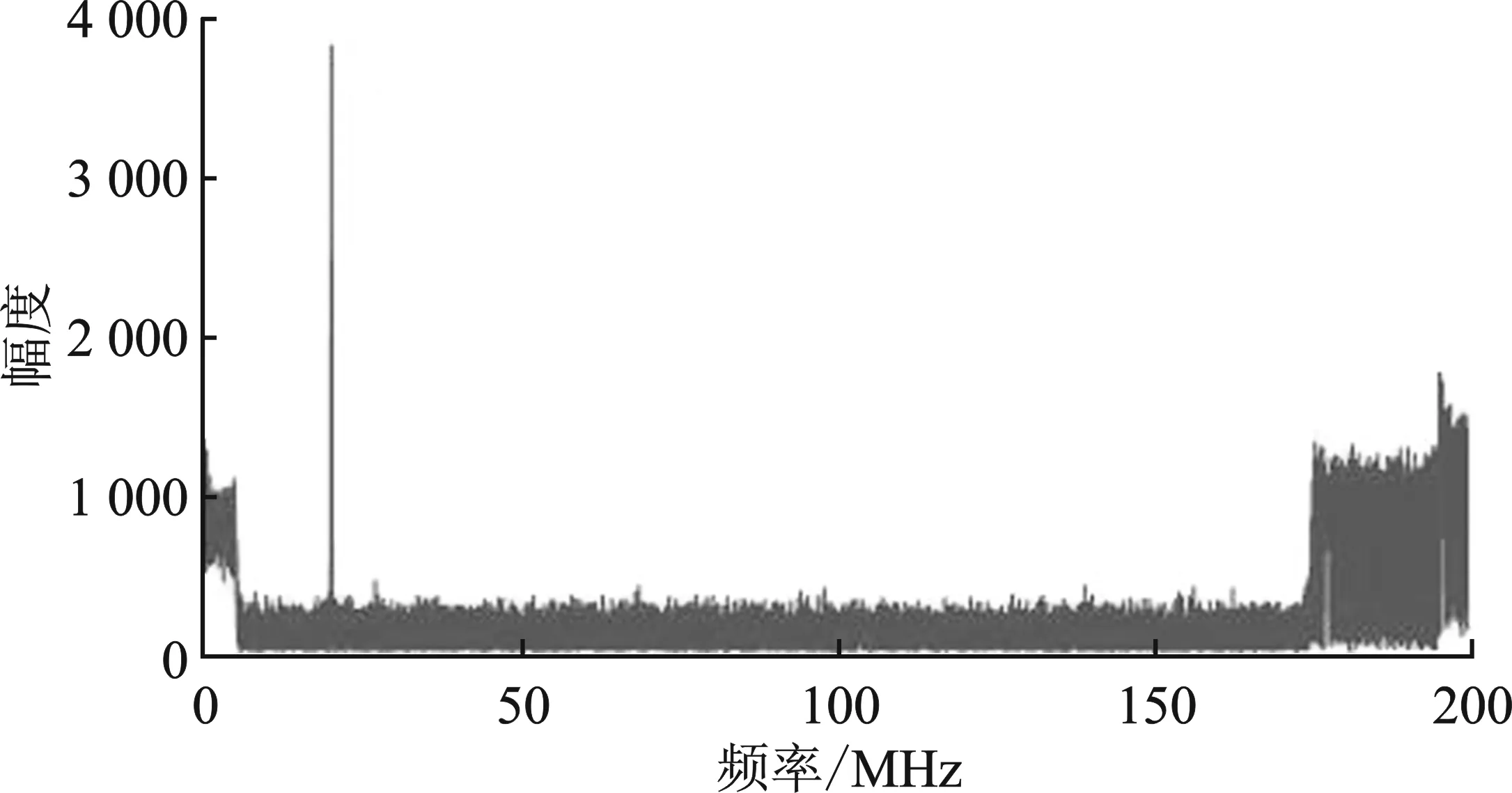
图5 处理后信号频域图
对图5中的信号进行带通滤波,通带中心为图该单频信号的频率。滤波后得到的信号的时域图为图6。此时复杂的混叠信号已经只剩下一个单频信号,只需测量它的脉冲到达时间和脉宽即可。
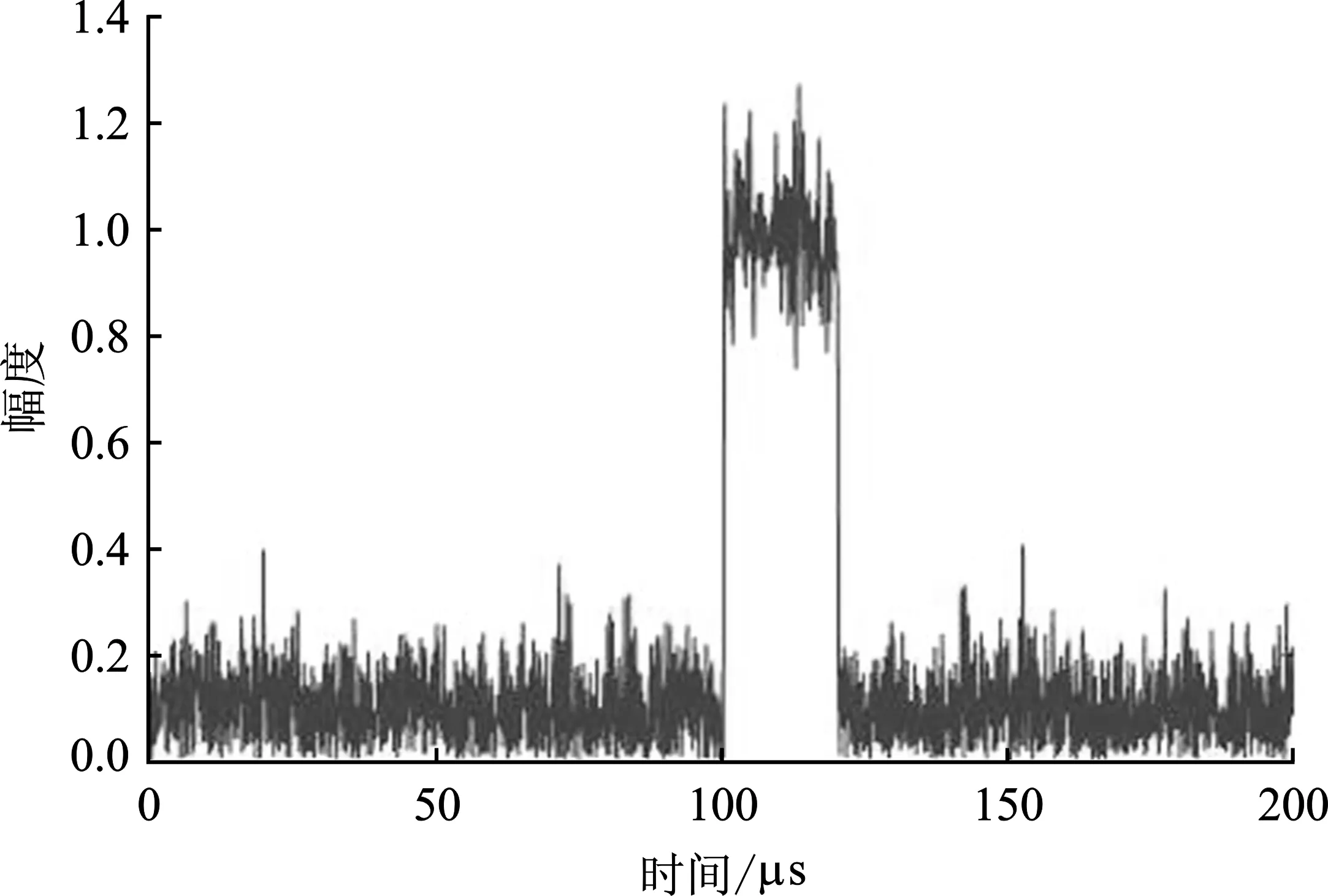
图6 滤波后信时域图
通过移位一点的自相关函数来最大地抑制噪声和积累信号能量,可更精确地测量信号起始时间,减少噪声对测量结果的影响。该单频信号的移位一点自相关函数如图7所示,此时通过简单地设置一个门限即可得到单频信号的脉冲到达时间和脉宽,得到原混叠信号中该单频信号对应信号分量的时域参数。
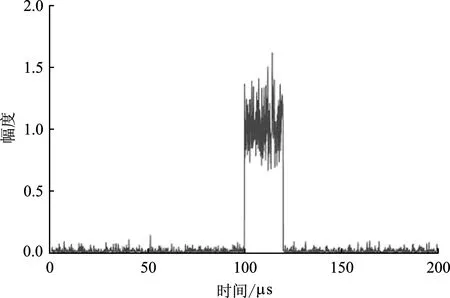
图7 自相关函数
本文以第3个信号分量的处理过程验证了提出的方法,重复上述步骤即可完成剩余分量的测量,进而完成所有信号分量的参数测量。具体测量结果如表3所示。

表3 混叠信号参数测量结果
5 结束语
本文研究了混叠脉冲雷达信号参数测量问题。针对HAF方法的参数测量方法只能得到信号相位系数而无法测得时域参数的问题,提出了基于HAF的混叠多分量LFM信号时域参数测量方法。该方法根据HAF方法得到的相位系数将LFM信号分量转变为单频信号分量,通过测量单频信号分量时域参数来得到原信号分量时域参数。本文方法既保留了HAF方法运算简单、精度高的优点,还改进了原本HAF方法不能测量时域参数的不足,并通过实验验证了方法的有效性。本文方法弥补了HAF方法的根本缺陷,为解决混叠脉冲雷达信号参数测量问题提供了一种新的方向与思路。

