基于bp神经网络的Bayesian-MCMC 方法在突发性水污染事件中的应用研究

□赵云峰 邢郡航

突发水污染事件具有突发性强、危害严重、影响广泛等特点。日趋加剧的水污染，已对人类的生存安全构成重大威胁，成为人类健康和经济社会可持续发展的重大障碍。而在我国城市化建设过程中，各种工业持续发展，工业经济为我国带来了巨大经济效益的同时，也为我们的生活带来了污染，我国的突发水污染事件也在不断增加，对人们的生活带来了很多弊端。不仅造成了较大的经济损失并产生社会影响，而且会产生生态危机，破坏人类生存的环境，严重影响了可持续发展的和谐社会构建。

突发性水污染不同于一般的环境污染，它具有不确定的突发性、影响范围的广泛性和危害的严重性等特点。水源地管理者需要增强突发性水污染事件应急处置系统的建设，强化突发水污染预测方法。

1.研究区概况

桃林口水库修建于滦河主要支流青龙河下游干流上，水库大坝位于青龙县三道河附近，坝址以上河长210km，控制流域面积5060km2，水库按100 年一遇洪水标准设计，1000 年一遇标准洪水校核，设计洪水位143.40m，校核洪水位144.32m，总库容8.59 亿m3。水库枢纽工程由主坝、正常溢洪道、泄洪洞、发电引水洞及水电站等组成。

桃林口水库是一座集供水、防洪、灌溉、发电等综合利用的大型水利枢纽工程，运行方式为多年调节。汛期与滦河上游的潘家口、大黑汀水库实施联合调度，调洪错峰，保障下游地区的防洪安全。水库为滦河中下游水资源开发骨干工程，主要任务为调节青龙河径流，供秦皇岛市城市和滦河中下游农业灌溉用水，结合供水发电，并起到部分消减洪峰作用，对冀东地区经济和社会发展具有十分重要的意义。

表1 算例中河流相关参数

表2 B 监测点浓度值

2.基于bp 神经网络的Bayesian-MCMC 模型计算方法与应用

2.1 模型概述

选取秦皇岛市桃林口水库上游大巫岚乡到双山子再到蛇盘兔河段为研究对象，全长6.57km，在二维稳态对流扩散模型的基础上，通过BP 神经网络获得先验概率分布，减少了原始方法中由于人的主观性造成的初始先验分布选取的误差，并在计算接受概率前，人工加入一个筛选条件，改进了马尔科夫链蒙特卡罗(MCMC)方法，大大减少了计算过程，并使计算结果更加精确，反演出污染源、污染量，并与改进前的贝叶斯马尔科夫链蒙特卡洛方法进行了结果对比分析。

本研究主要分为污染物二维扩散模型、参数率定方法、模拟算例3 大模块，分别给出了污染物扩散的二维一般模型、贝叶斯原理和改进的Bayesian-MCMC 方法，以及算例和成果对比分析等内容。

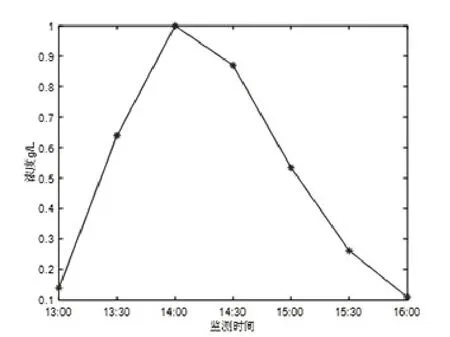
图1 断面B 处污染物浓度变化曲线

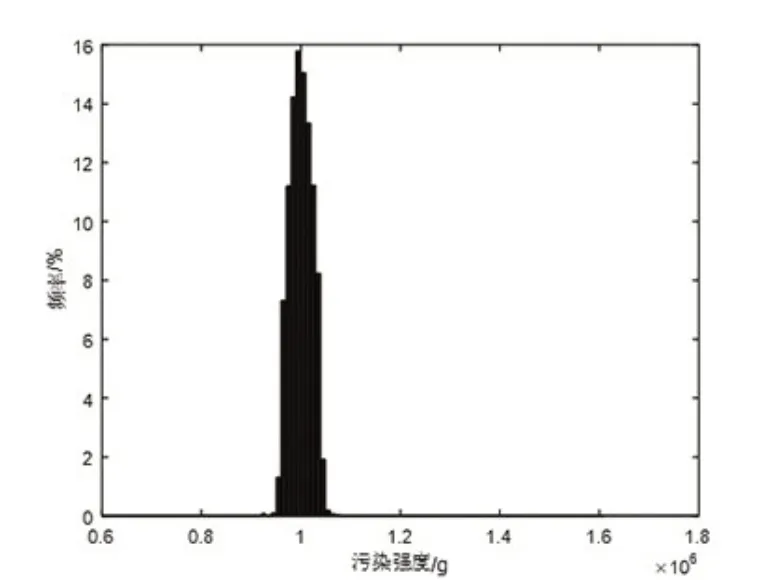
图3 误差水平为0.05 污染强度M 的后验分布直方图

图4 误差水平为0.1 时的迭代曲线

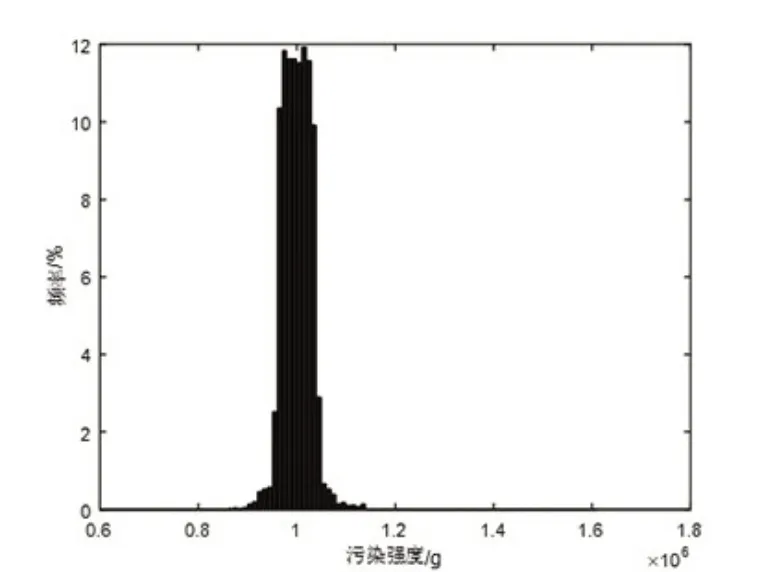
图5 误差水平为0.1 污染强度M 的后验分布直方图

2.2 模型创建

改进后的Bayesian-MCMC 方法的具体算法原理与步骤如下：

①利用bp 神经网络确定污染强度的先验分布；

②在模型参数先验范围内随机生成一个初始值M；

③利用污染物扩散模型计算出初始值M(1)对应的污染物浓度序列C1 及其对应的条件概率密P；

④从Proposal 分布中生成候选参数M′,计算此参数对应的污染物浓度序列C2及其对应的条件概率密度P’；

⑤进行一次筛选：当∑∣C1-C2∣＜0.15 时，转下一步,否则不接受，M(i+1)=M(i)；

⑥计算接受概率：α=min｛1，p′/p｝；

⑦从[0,1]中产生一个随机数u，如果u＜α,则接受候选参数并使P=P′，即M(i+1)=M′，否则不接受，M(i+1)=M(i)；

⑧重复③～⑦,直到达到迭代次数。

二维稳态对流扩散方程可以表述为：

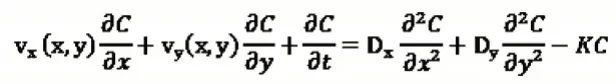
式中：

Vx（x，y），Vy（x，y）—x，y 方向的流速，m/s；

C(x，y，t)—污染物浓度，mg/L；

Dx，Dy—河流横向、纵向扩散系数，m2/s；

K—降解系数S-1。

对于瞬时点源排放，方程的解析解可表述为：

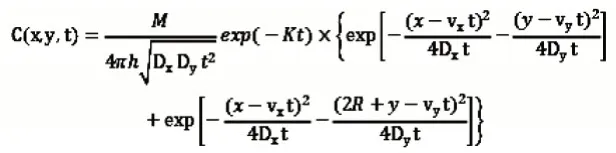
式中：

M—污染物排放量，mg；

h—水深，m；

R—污染点到边界的距离，m；其他同上。

2.3 模型的应用

模拟算例假设条件如下：在11∶00时，距双山子水文站上游5km 的某断面A 处发生了污染，污染强度为Mg，现在双山子水文站，监测污染物浓度变化，初始监测时间13∶00 时，距污染发生2小时，假设该河段含水层类型为二维均质各向同性，稳定均匀流，河流各水文条件稳定，满足二维污染物扩散模型的应用条件，污染物排放为瞬时岸边排放，污染物为保守物质，即不考虑任何化学反应，所需模型参数见表1，B 监测点浓度数据见表2。

表2 中数据用图像表示，见图1(大致呈正态分布)。

按照改进的Metropoli 算法的原理与步骤，在误差水平为0.05 时，利用matlab 迭代10000 次 之后去除燃烧期(初始迭代次数)的结果见图2。

污染强度M 的后验分布直方图见图3。

程序运行总时间为1.598s。

在误差水平为0.1 时，迭代10000次之后的结果见图4。

污染强度M 的后验概率直方图见图5。

程序运行总时间为3.090s。

由图2 和图4 中可以看出，迭代曲线最终达到稳定，马尔科夫链的最终状态平稳分布；由图3 和图5 中可以看出，污染强度M 的后验分布为正态分布。污染强度在1×106附近的频次最大，符合预先假定的初值。

3.结语

突发性水污染事件其本身具有很强的不确定性、包括发生污染的时间地点，污染物种类、浓度等，从而使得率定此类模型具有较强的不适定性。为此，本研究采用改进后的Bayesian-MCMC方法，对在桃林口上游双山子河段的模拟案例进行处理分析，得到了较为理想的结果，Bayesian-MCMC 方法具有更高的精确性和稳定性，是一种很好的处理水污染问题的方法。

在研究过程中，本研究采用的Bayesian-MCMC 方法对水源地水污染事件污染源进行追溯和评估，研究过程中在一、二维交接面处引入了流速、水位等物理量的二次分布函数。随着资料的积累，选用二次函数作为各物理量在交界面分布的拟合函数，寻找更精确的分布函数还有待进一步研究。