食饵染病的交错扩散捕食模型整体解的存在性和渐近性

陈清婉, 柳文清

(闽南科技学院,福建 泉州 362300)

本文讨论高维情形下食饵带有疾病且具有交错扩散的捕食-食饵模型:

(1)

假设Ω⊂Rn是具有光滑边界的有界区域,齐次Neuuman边界条件表明整个生态系统是封闭的.u1,u2,v分别表示染病食饵、未染病食饵以及捕食者种群密度函数;a1,a2分别表示食饵种群的内禀增长率,a3可以为负,其他参数均为正数;b1,b2分别表示捕食者对食饵捕食的捕获率,疾病只在食饵之间传播并且假设捕食者也捕食染病食饵,疾病传播率为r;β1,β2表示食饵转化为食物的转化率,在文中,总是假设β1>β2.d1,d2,d3表示3种群的扩散率,它是由空间分布不均匀引起的扩散;a11,a22,a33表示由于群内竞争而引起自扩散,a31,a32是交错扩散系数,它是由种群间相互作用引起的扩散.一般认为:一种群带正的交错扩散系数表示该种群从另一种群密度高的地方向密度低的地方扩散,模型(1)中具体表现为食饵的集体防御捕食者,而一种群带负的交错扩散系数表示该种群从另一种群密度低的地方向密度高的地方扩散,模型(1)中具体表现为食饵的逃离捕食者.

两种群Lotka-Volterra竞争型交错扩散模型首次由Shigesada-Kawasaki-Teramoto[1]提出,其局部解的存在唯一性由Amann在文献[2—4]中给出,然而古典解的整体存在性至今仍然没有解决,证明的难点主要在于交错扩散的影响.近年来,很多学者研究了一些特殊情形下交错扩散模型整体解的存在性.例如去掉一些交错扩散系数且空间维数有限(n<6)时古典解的整体存在性(参考文献[5—8]),或者在一维情形且交错扩散矩阵正定时古典解的整体存在性(参考文献[9—10]),证明的方法主要是能量估计和bootstrap技巧.文献[11]考虑了一类带Holling Ⅱ型反应函数的捕食食饵交错扩散模型,利用文献[12]中命题2.1,证明了空间维数n<10时古典解的整体存在性.本文将讨论模型(1)古典解的整体存在性,在此基础上进一步证明解的渐近性.其主要结果如下:

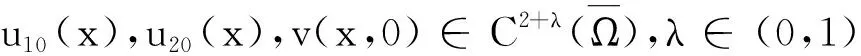
定理2当下列条件满足时:

E*是全局渐近稳定的.

1 整体解的存在性

记QT=Ω×(0,t),t∈(0,T),先证明如下引理.

引理1设(u1,u2,v)是问题(1)的解,则存在正常数M0,M1,M2使

0≤u1≤M0, 0≤u2≤M1,

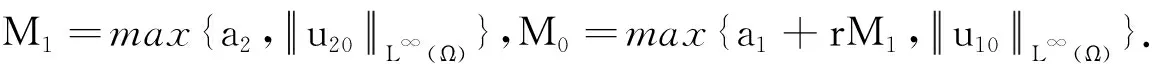
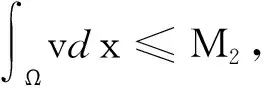
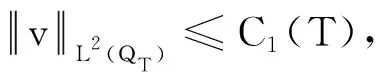
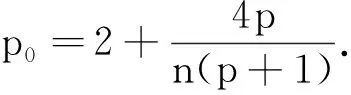
引理4存在正常数C3(T),C4(T)使得

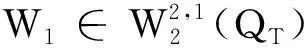
W1t=(d1+2a11u1)ΔW1+

u1(a1-u1-b1v+ru2)W1.

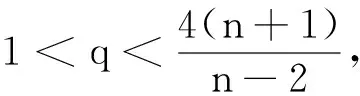
证明将方程组中的第3个方程两端同时乘以qvq-1并在Ω上积分可得

β1b1u1+β2b2u2)dx.

(2)

上式在(0,t)积分得

(3)

注意到

(4)

从而

由Hölder不等式和Poincare不等式可得

(5)

由Hölder不等式结合引理4可得

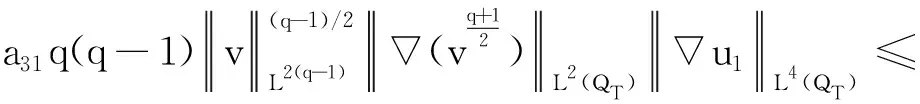
同理

所以

(6)

将(4)～(6)式代入(3)式中,整理可得

(7)

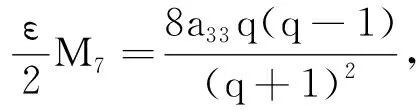
(8)

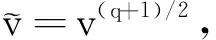
则有

(9)

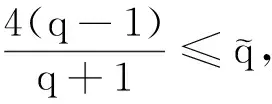
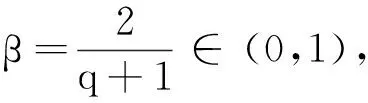
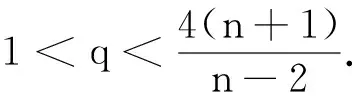
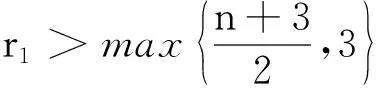
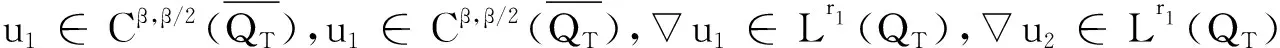
2 解的渐近性质

通过简单计算可知,当下列条件满足时:

β1≥β2,

a2β2b1b2-rb2a3>0,

a1β1b1b2+rb1a3>0,

D3=(r2+1)a3+a1β1b1+

(β1b1r+β2b2)a2-β1a1b2r>0,

系统(1)有唯一正平衡解

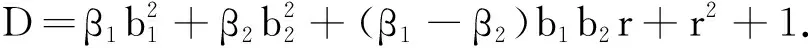
定理2的证明定义Lyapunov函数:

在t>0求导可得

利用格林公式化简可得

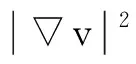
(a31u1+a32u2)v*v](v2)-1dx-

取λ=β1,ρ=β2,结合定理条件并利用Young不等式可得