基于AutoForm的汽车翼子板冲压回弹仿真及补偿研究*

蒋磊 吕中原 王龙 谢蛟龙 马培兵 张雄飞（东风本田汽车有限公司新车型中心）

汽车覆盖件在成形负荷卸载后，一部分弹性变形会发生回复，从而产生回弹[1-3]。回弹是汽车覆盖件成形工艺中难以避免的缺陷，对汽车覆盖件的尺寸精度起着决定性作用[4-6]。对于汽车外覆盖件，由于造型曲面多样化、装配结构复杂化，在冲压成形后所产生的回弹往往会更大[7-9]。如何降低回弹，提高汽车外覆盖件的尺寸精度一直是汽车制造工艺领域的热点课题。为了准确预测汽车外覆盖件的冲压回弹，国内专家学者进行了诸多研究。文献[10]研究了6014-T4铝合金汽车发动机罩外板成形工艺及冲压回弹，控制了最大回弹量。文献[11]运用AutoForm软件分析了汽车翼子板前门区域的回弹，解决了翼子板前门区域尺寸超差问题。文献[12]分析了汽车顶盖各成形工序的回弹，提高了CAE分析的准确性。文献[13]对汽车后门外板自由回弹和夹持回弹进行了对比分析，得出了满足尺寸公差要求的零件。上述研究对于回弹的解决基本局限于拉延、整形或翻边工序的模具型面补偿，对于修边、冲孔工序的回弹不确定性，以及全工序压料板闭合过程中所带来的塑性变形极少考虑，故而无法高度再现实际试模工况，回弹补偿方案的稳健性往往难以保证。基于以上现状，文章以某汽车翼子板为研究对象，介绍了一种更加贴近实际生产工况的回弹仿真与补偿方法，提高了回弹补偿精度，减少了试模次数，节约了模具调试成本。

1 工艺分析

图1 为某汽车翼子板产品几何模型，所使用的材料牌号为JAC270D-45/45，属于一种深冲用双面等厚热镀锌汽车用钢，等同于宝钢DC54D+ZF-45/45，材料特性为：屈服强度YS=120～200 MPa，抗拉强度TS=260～350 MPa，各向异性指数r≥1.8，加工硬化指数n≥0.2，断面延伸率El≥34%。产品轮廓尺寸为1156mm×774 mm×237 mm，材料厚度为0.65 mm。该零件具有造型起伏急剧、A面曲率大、特征棱线圆角小、结构面负角多以及成形深度大且不等深等特点。

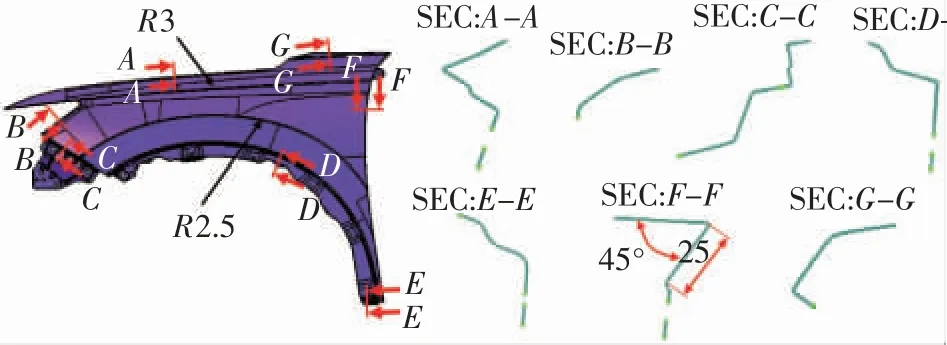
图1 翼子板几何模型

结合产品结构特点对翼子板成形工艺进行分析：零件成形深度较大，且绝大部分型面为A级曲面，外观质量要求高，因此需要采用一次拉延成形工艺；对于其余存在负角的结构面则需要采用先过拉延后整形的成形工艺；由于翼子板本身尺寸不大，可在一道工序内完成全部外缘修边；前门匹配区域为45°夹角的负角法兰，法兰宽度较大，达到25 mm，直接一次侧整形到位会导致外观面产生严重的面畸变，因此需要采用先预翻边后侧翻边的成形工艺。综合考虑冲压模具的设计难度和制造成本，确定了翼子板4工序的成形工艺方案，如图2所示。

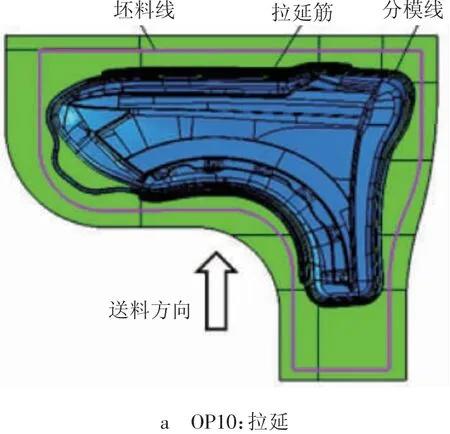
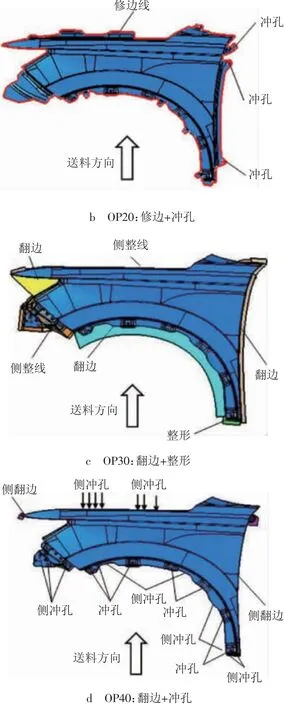
图2 翼子板冲压工艺方案

2 初步回弹评估

为了准确地预测翼子板全工序冲压回弹，使CAE分析能够高度再现真实工况条件，对于拉延之后的各工序压料板闭合所导致的额外变形必须加以甄别并进行剔除。因此，需要采用类比法筛查制品在压料板闭合过程中所产生的塑性变形。具体做法为：（1）进行全工序冲压成形仿真，回弹仅计算最终工序，并将回弹类型设置为最小夹持回弹；（2）逐一对各工序进行冲压成形及回弹仿真，其中，最后一道工序为最小夹持回弹，其余工序为自由回弹；（3）对比两种不同模拟方法下的翼子板回弹仿真结果差异。两种模拟方法分析流程如图3所示。

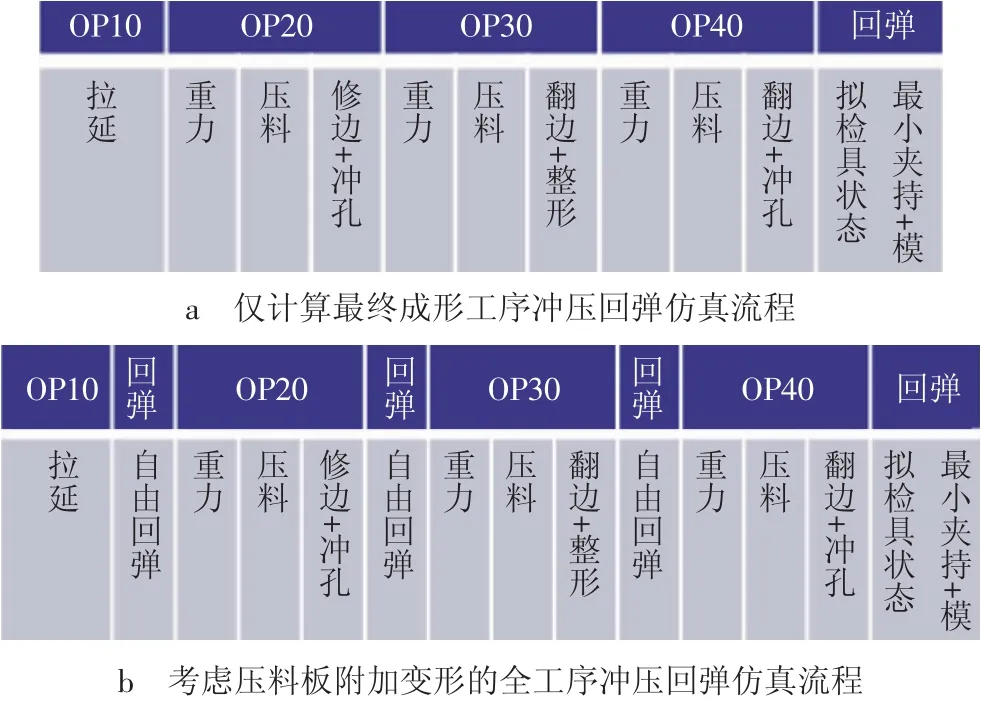
图3 2种冲压成形回弹仿真流程

将按照4工序工艺方案设计的翼子板冲压工艺模面、冲压坐标系、坯料线等数据以IGS格式导入Auto-Form，完成各工序冲压方向、工具体、工艺参数以及仿真精度设置后，按照图3两种不同的仿真流程分别进行全工序回弹计算，回弹仿真结果分别如图4、图5所示。

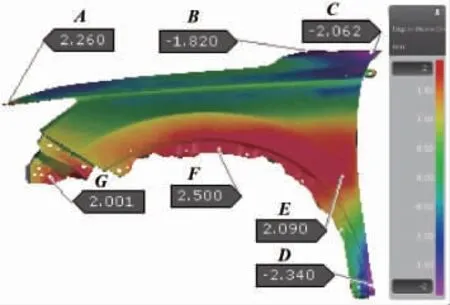
图4 仅计算最终工序最小夹持回弹仿真结果界面

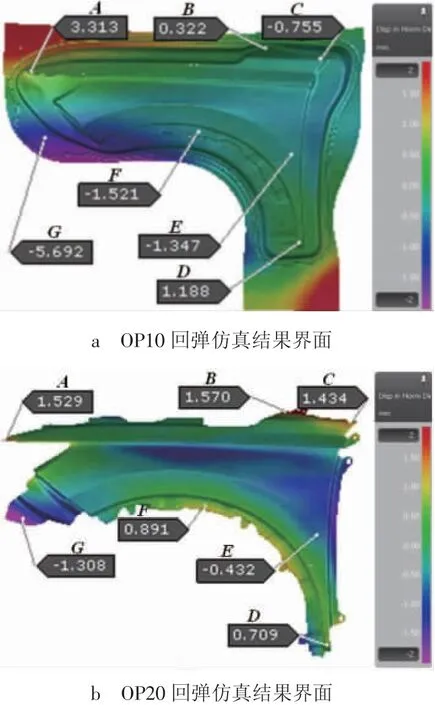
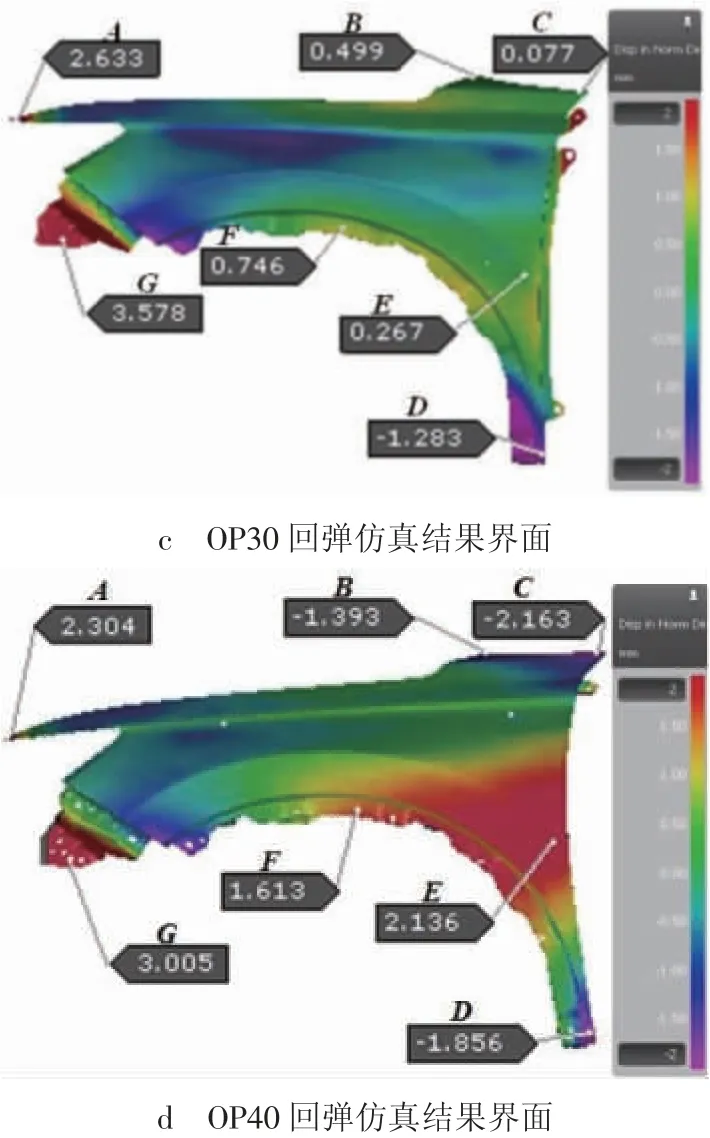
图5 考虑压料板附加变形的全工序冲压回弹仿真界面

选取图5所示回弹量较大的区域设置测点，分别记为测点A、B、C、D、E、F、G，并在测点部位进行回弹量取值，然后与图6所示回弹量进行对比，对比结果如图6所示。由图6可知，两种不同模拟方法的最终回弹趋势基本一致，翼子板多处回弹远大于制品±0.5 mm的尺寸精度要求，全工序均存在较大的回弹，且OP10、OP20、OP30均存在局部区域回弹趋势与最终回弹趋势不一致的现象。说明制品在中间工序成形过程中产生了额外的塑性变形，从而导致回弹区域发生变化。

图6 2种模拟方法的回弹量对比

虽然仅计算最终工序最小夹持回弹与考虑压料板附加变形的全工序回弹在趋势上保持一致，但各部位回弹数值差异较大，表明中间工序的回弹对制品最终回弹的影响不可忽略。因此，为了更真实地模拟制品的冲压回弹，采用考虑压料板附加变形的全工序回弹仿真方法更为合理。

3 压料板附加变形剔除

在实际生产中，为了减少冲压模具的加工和研配工作量，后工序压料板并非全型面压料，对于修边、冲孔类模具，仅保留工作刃口附近10～20 mm宽的有效压料面，对于翻边、整形类模具，仅保留工作刃口附近20～30 mm宽的有效压料面，并对压料板型面上R10 mm以下的圆角进行避空。因此，为了将压料板闭合对冲压回弹的影响降至最低，需要对翼子板冲压工艺模面进行优化，即按照冲压模具实际工况条件，对后工序压料板工艺数模非工作区域以及小圆角区域进行镂空设计，后工序压料板优化后的工艺模面如图7所示。

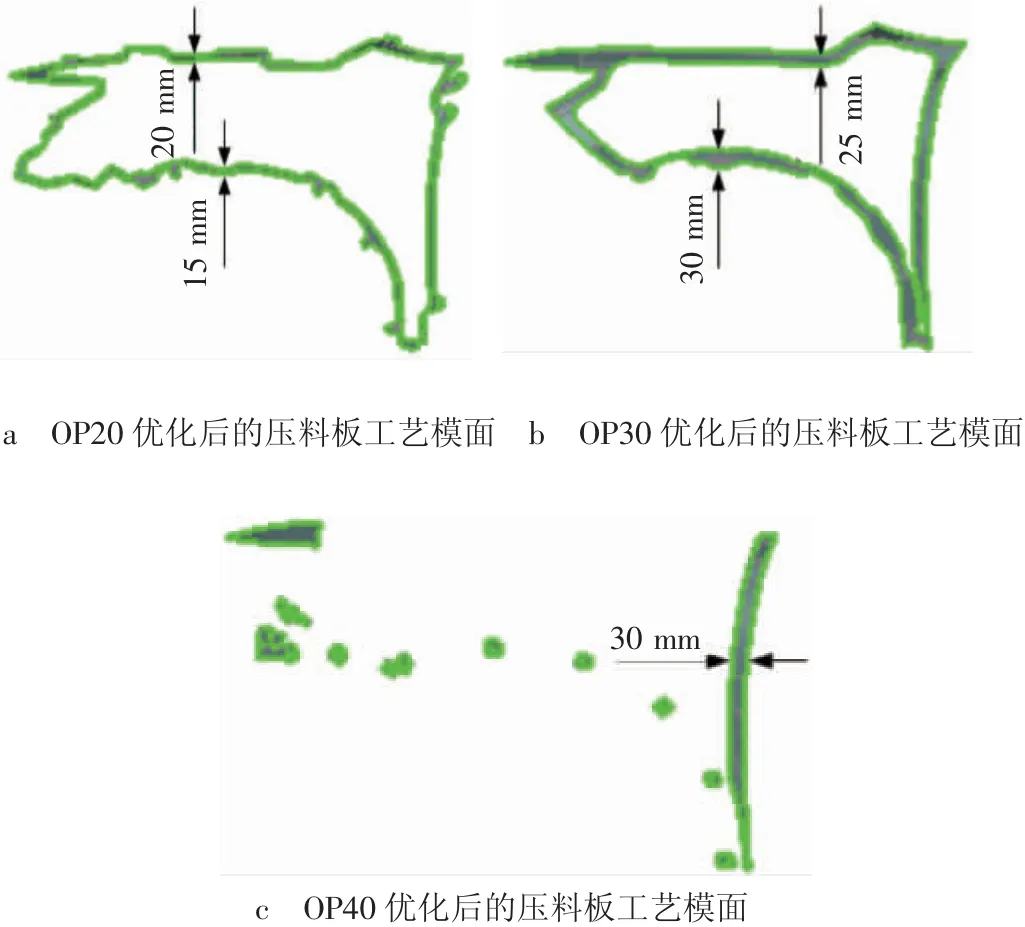
图7 优化后的压料板工艺模面

将优化后的工艺模面再次导入AutoForm求解计算，得出如图8所示的全工序冲压回弹仿真结果。由图8b、8c、8d可知，剔除后工序压料板闭合所导致的附加变形后，除测点E、G区域回弹量仍然较大、且前后工序间回弹存在波动以外，其余部位回弹量均已降至±1 mm以内，同时前后工序之间的回弹波动也较小。

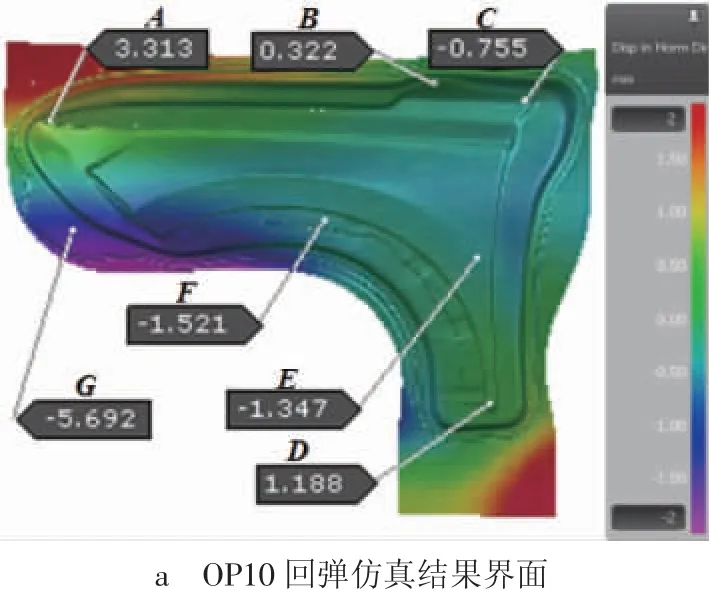
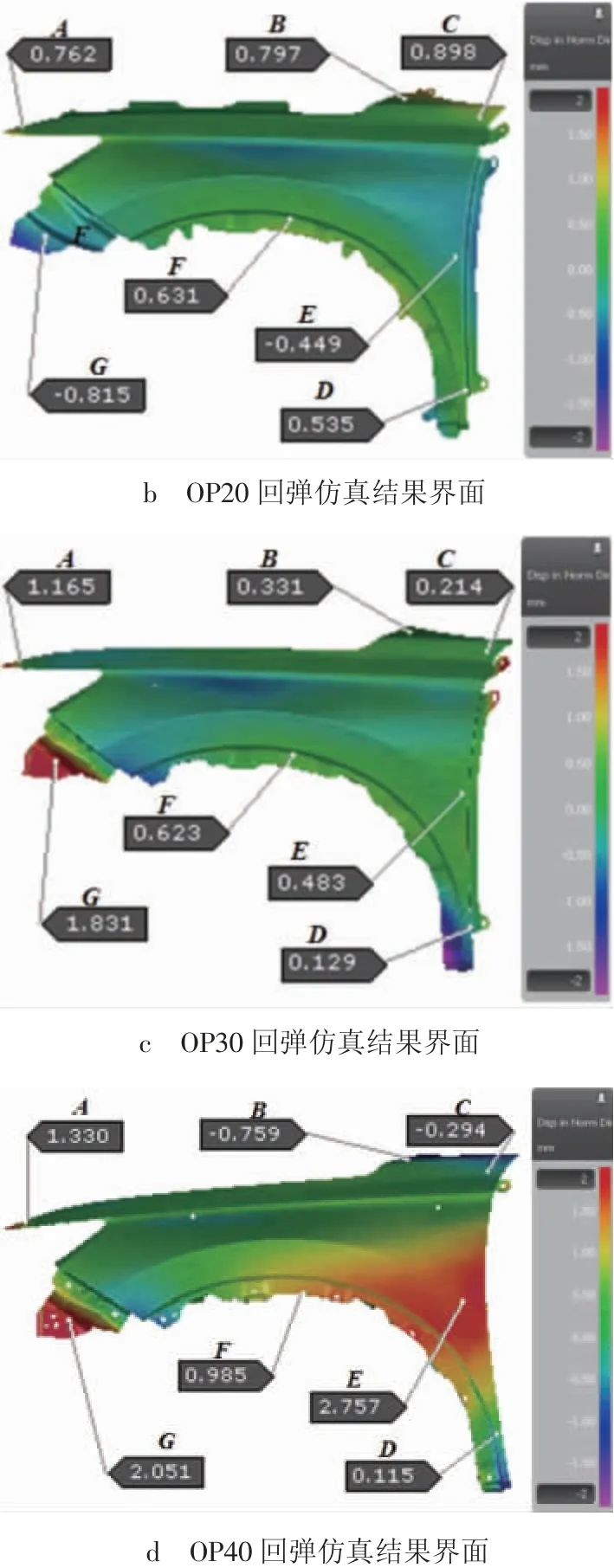
图8 剔除压料板附加变形的全工序冲压回弹仿真界面

4 回弹补偿研究

由图8可知，虽然剔除压料板附加变形后，翼子板最终回弹有所降低，但仍不满足±0.5 mm的尺寸精度要求，因此需要对冲压模具进行回弹补偿，以进一步降低制品回弹。目前，业内常规的回弹补偿策略为全工序回弹补偿法，即根据各工序回弹量的不同，分别在对应的模具上进行型面补偿。这种补偿策略虽然最终都能够实现回弹的有效控制，但是由于各工序间均存在模具型面差异，导致回弹非线性加剧，使其更难准确预测，从而导致前期回弹补偿计算迭代次数成倍增加、仿真效率低下，后期试模周期长、冲压模具需要反复改修验证。

为了解决这一问题，可以对全型面补偿策略进行优化，引入继承补偿概念，即将回弹量较小的修边、冲孔工序型面补偿量复合至回弹量较大的拉延、整形工序，对于修边、冲孔工序的回弹则不再进行补偿。优化前后的全型面补偿策略如图9所示。

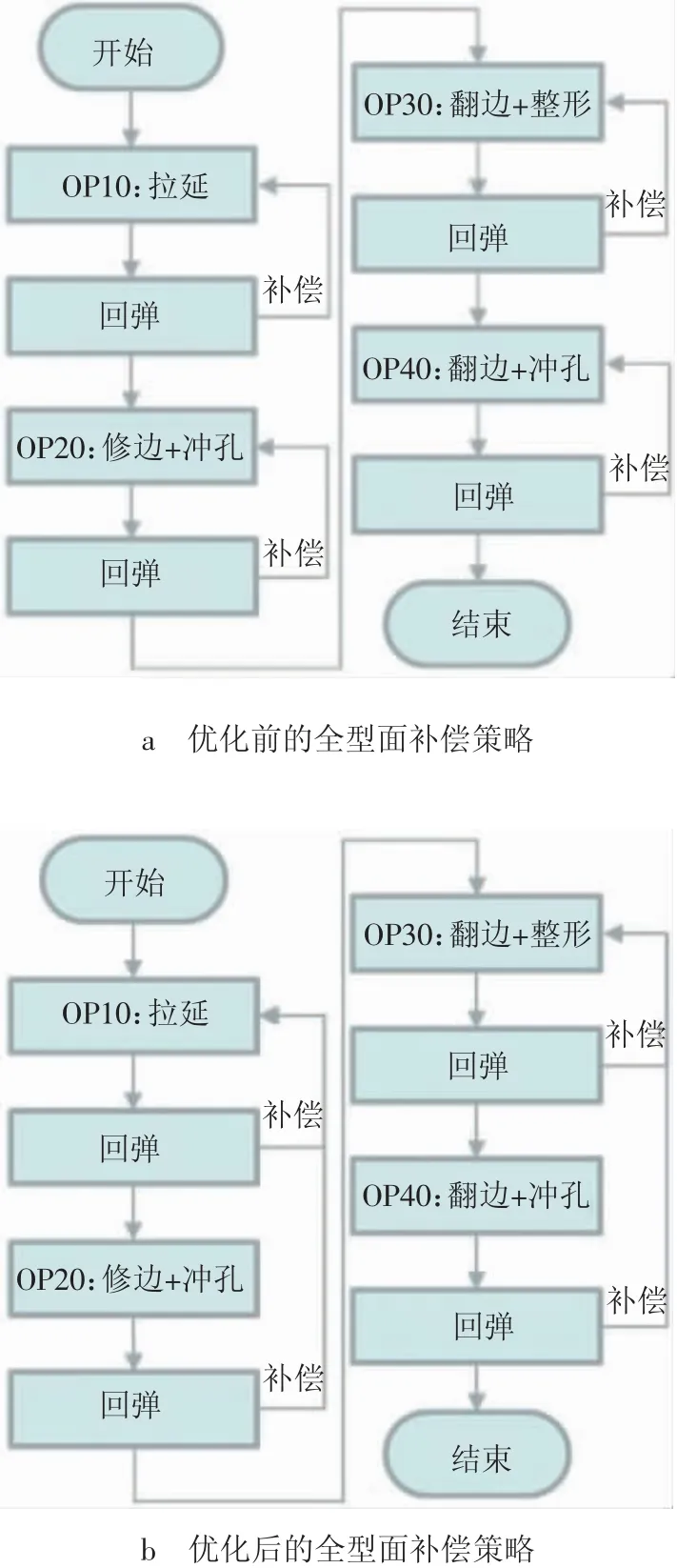
图9 优化前后的全型面补偿策略

AutoForm回弹补偿模块可基于回弹仿真结果进行自动补偿，利用优化后的全型面补偿策略对翼子板进行回弹补偿，补偿之后再次求解计算，并将回弹仿真结果与制品几何模型进行对比。若回弹量仍然大于0.5 mm，则启动新一轮的迭代循环；若回弹量小于0.5 mm，则可将各工序有限元模型以IGS格式导出作为回弹补偿精细化设计的基础数据。

由于翼子板属于汽车外覆盖件，AutoForm导出的回弹补偿数据无法直接用于模具型面加工，因此需要使用CATIA软件对从AutoForm导出的IGS格式数据进行曲率连续性修正和缝合，使所有A级曲面均达到G2连续，最终精细化设计的A面回弹补偿数据光顺性检查如图10所示。

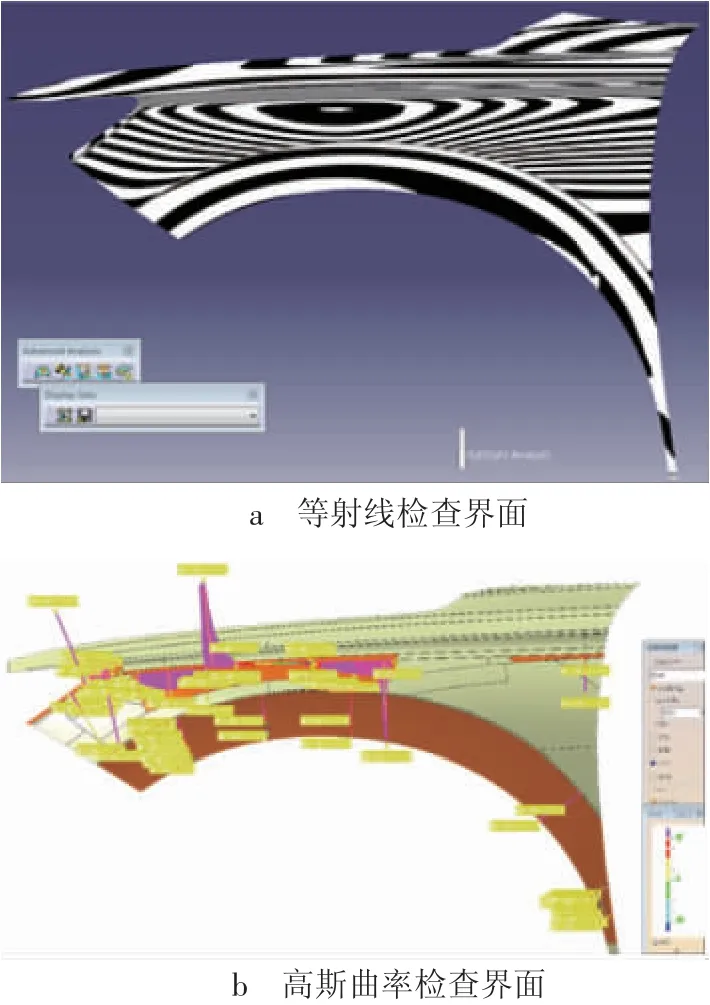
图10 最终回弹补偿数据光顺性检查界面

将利用CATIA精细化设计的回弹补偿数据再次导入AutoForm进行最终回弹分析验证，得出如图11所示的翼子板回弹仿真结果。由图11可知，经过回弹补偿后，翼子板最大法向回弹位移为0.489 mm和-0.405 mm，所有区域回弹量均已全部降至±0.5 mm以内，达到了零件尺寸精度要求。

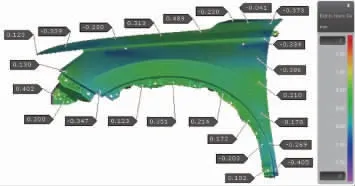
图11 最终回弹补偿仿真结果界面

5 方案验证

将最终回弹补偿数据应用于翼子板冲压模具，并按照回弹仿真结果进行翼子板现场试模，得到无开裂、起皱等质量缺陷的合格零件。利用检具对翼子板进行尺寸精度测量，制品实际面轮廓尺寸偏差测量如图12所示。检具测量结果表明，翼子板零件回弹得到了有效控制，装配部位的尺寸偏差全部在±0.5 mm以内，满足零件生产以及整车匹配需求。

将翼子板零件实际尺寸精度测量数据和回弹仿真结果进行对比分析，其结果如图13所示。由对比分析结果可知，试模试验与仿真数据基本吻合，最大偏差仅0.2 mm，证明采用基于继承补偿理念的全工序回弹补偿策略对于提高回弹仿真精度、减少试模改修次数有着重要的指导意义。

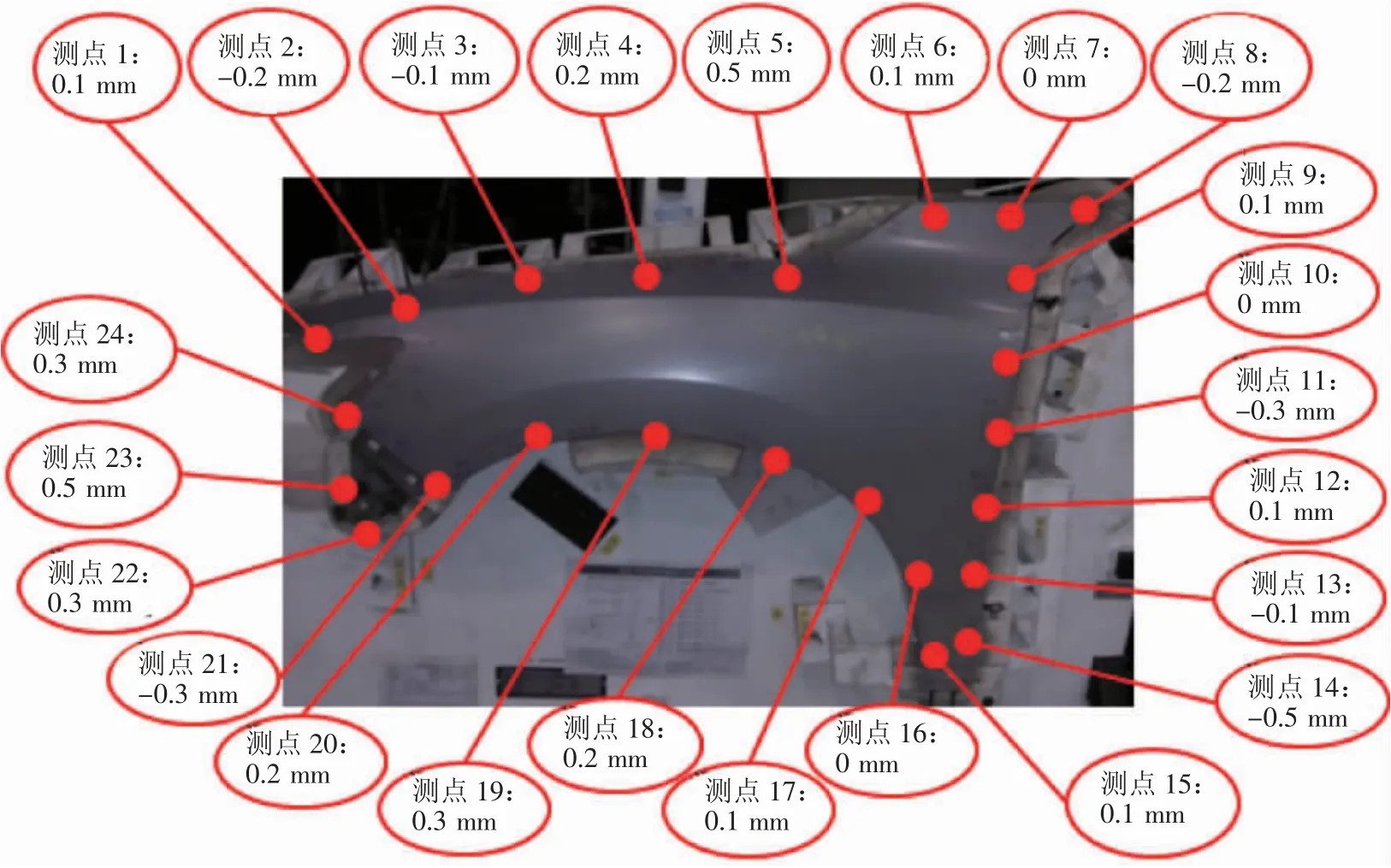
图12 翼子板零件尺寸精度检具测量数据

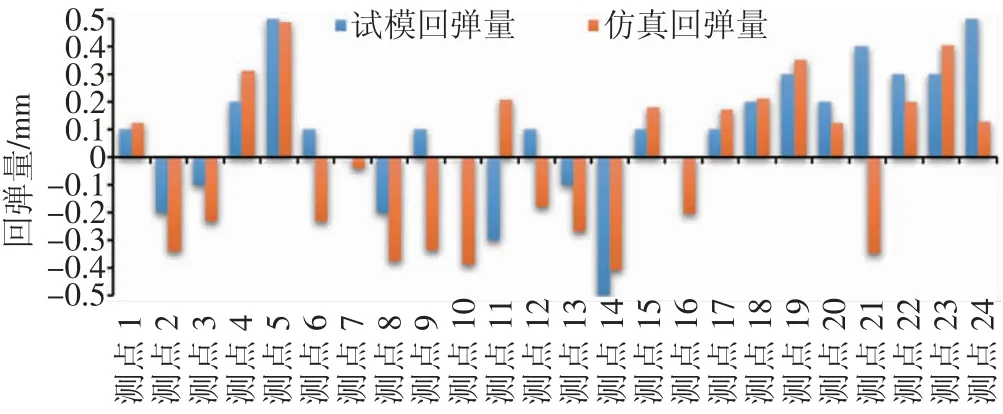
图13 试模试验与仿真结果对比

6 结论

（1）对于造型多样、结构复杂的汽车外覆盖件，剔除后工序压料板闭合对制品真实回弹的影响，更贴近实际生产工况条件，能够使回弹仿真获得更高的预测精度。

（2）运用继承补偿方法优化全工序回弹补偿策略，降低了回弹补偿迭代次数以及尺寸波动的不确定性，将翼子板全型面回弹量控制在0.5 mm以内，解决了翼子板回弹大、不可控的难题。

（3）试模试验验证了基于继承补偿法的全工序回弹补偿策略的有效性，提高了冲压模具回弹补偿设计效率、减少了现场试模次数、节约了模具调试成本，对于同类零件的回弹仿真以及补偿有一定的工程应用价值。