基于位移光栅尺的拉伸法弹性模量测量

孙 瑜，宋连鹏，周 丽

(海军大连舰艇学院 基础部，辽宁 大连 116018)

弹性模量是研究材料力学性能的重要参量之一，它是表征物质材料在弹性限度之内抗压或抗拉的物理量. 随着工业生产和科学技术的蓬勃发展，对微小尺寸的测量越来越重要，同时对于量度的准确性也提出了愈来愈高的要求.

常采用拉伸法测量弹性模量，设金属丝长度为L，横截面积为S，若将其一端固定，在另一端施加拉力F，则在此拉力作用下，金属丝产生微小的伸长量ΔL. 根据胡克定律，在弹性限度内，物体的应力与应变成正比，即

(1)

式中比例系数Y为金属材料的弹性模量.

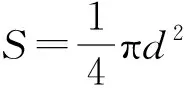
(2)

由于在拉伸法测量弹性模量的过程中，微小形变量的测量精度是测量的关键因素[1-2]. 而位移光栅尺以其高精度、高稳定性在测量中得广泛应用.

本文结合位移光栅尺的测量优势[3]， 将其应用在拉伸法弹性模量测量中，也是对实验技术和实验手段的尝试与改进.

1 位移光栅尺测量系统的设计

1.1 测量系统构成

本系统主要由弹性模量测定仪和位移光栅尺组成，辅助测量仪器为螺旋测微计和直尺，如图1所示.

图1 位移光栅尺测量系统

实验选择国产的JCS900-2AE位移光栅尺，如图2所示. JCS900-2AE位移光栅尺结构简单、小巧、性能稳定、性价比高，主要用于测量微小形变量，光栅常量[4]为20 μm，精度为±5 μm. 测量结果可通过数显表直接读出.

图2 JCS900-2AE位移光栅尺

1.2 系统测量原理

由于动尺与金属丝粘合在一起，所以动尺将会随着金属丝的拉伸而移动，其移动距离Δl即为金属丝受力后的微小形变量，如图3所示，微小形变量是金属丝顶部固定端到动尺固定端长度l所产生的形变量Δl，Δl的数值大小将由光栅尺的数据采集系统采集计算后，在数显屏上显示[5-6]. 由(2)式可知，F为砝码重力，所以只要再测量出金属直径d，即可求出金属丝的弹性模量值. 即测量表达式为

(3)

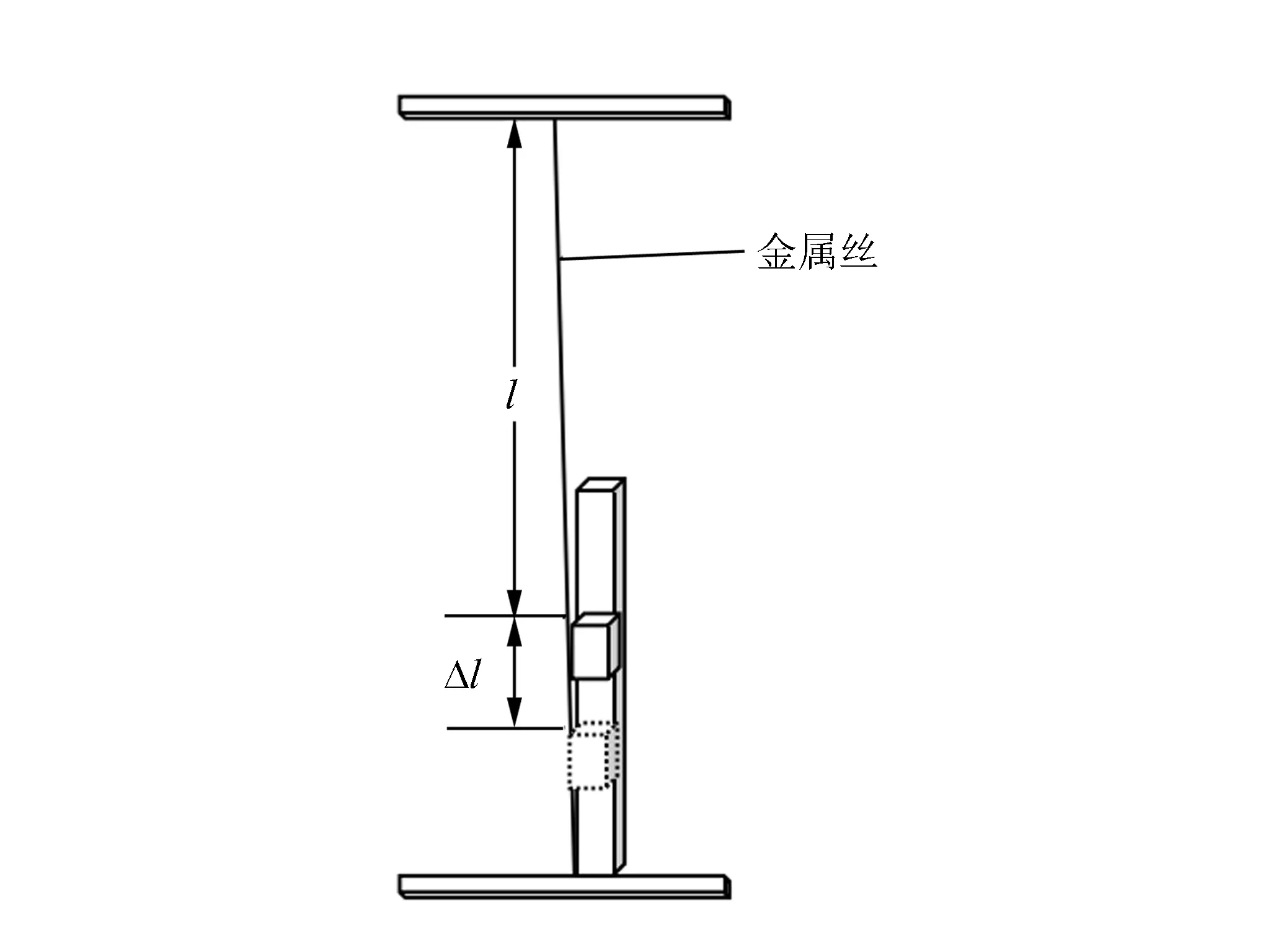
图3 微小形变量测量原理图

2 测量数据处理与分析

利用位移光栅尺测量系统，记录增荷减荷时位移光栅尺的位置读数,如表1所示，测量金属丝的长度及直径L=76.10 cm，d=0.587,0.588,0.581 mm，代入测量式(3)中，计算金属丝的弹性模量. 通过对测量结果的误差处理，并与光杠杆放大法进行比较发现，利用位移光栅尺测量系统可降低测量结果的相对误差.

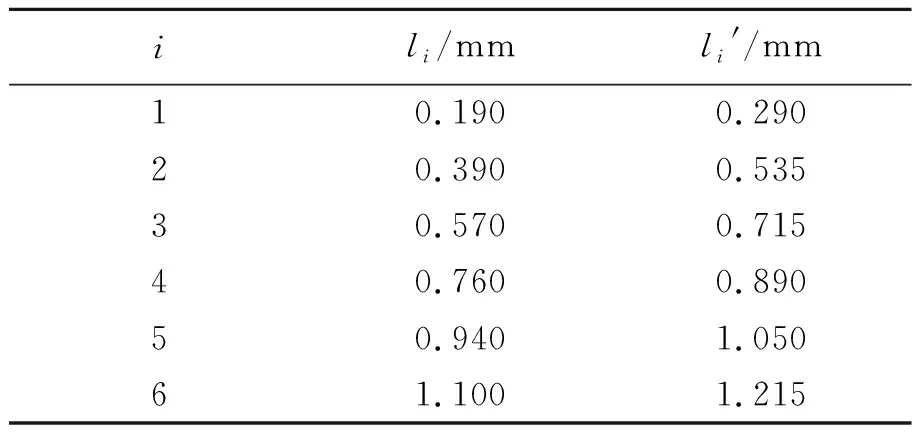
表1 增减荷时光栅尺读数

2.1 微小形变量Δl的数据处理分析

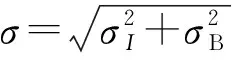
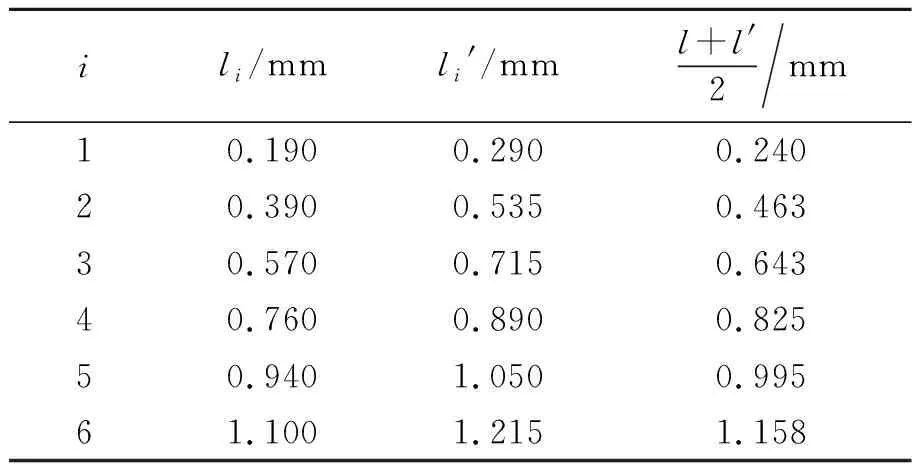
表2 光栅尺读数记录与处理(单个砝码质量)

由表2中数据可以得出，增减砝码时金属丝的长度变化比较均匀，同时也发现，在同一数量砝码的负荷下，增荷与减荷时读数有一定的偏差，这是由于金属丝的弹性滞后性造成的. 运用最小二乘法对数据进行处理得到金属丝受到单个砝码的重力作用时的伸长量为：

2.2 L、d的数据处理分析

L、d同样为直接测量量，其各自合成不确定度参见上述直接测量量的计算方法,其中L为单次测量,则L的测量结果表达式为：

d的3组测量数据0.587,0.588,0.589 mm，经零点读数修正后，进行处理得到其合成不确定度.

得到金属丝直径d的测量结果表达式为

2.3 弹性模量Y的数据处理分析

最后将测量量的平均值代入到式(3)中计算得到弹性模量为：

求出σY=0.06×1011N/m2. 所以Y的最终计算结果为：

Y=(1.59±0.06)×1011N/m2.

计算结果符合国际标准给出的金属丝的弹性模量值范围，由于实验中减少了变量数量，且光栅尺的精度较高，因此，计算结果的不确定度σY=0.06×1011N/m2. 而传统拉伸法的测量不确定度为σY=0.1×1011N/m2，测量精度有了显著的提高.

3 结束语

通过参考相关文献，本文提出了利用位移光栅尺测量弹性模量，基于拉伸法和位移光栅尺测量原理搭建了测量系统，利用光栅尺取代了光杠杆放大法测量微小形变量，实现了对金属丝弹性模量的测量. 实验结果表明提出的测量方法有效可行，且提高了测量精度.