基于共线外差干涉的波片相位延迟的测量系统
周 森,张志伟,b,杨娅洲
(中北大学 a.信息与通信工程学院;b.电子测量技术重点实验室,山西 太原 030051)
波片是光轴方向平行于晶体表面的双折射晶片,作为偏振光学技术和光学系统中的重要元件,它被应用在各种研究领域. 例如,波片可以在椭偏法测量或相移干涉测量中对偏振光的偏振态进行调制;用在太阳磁场测量设备的偏振分析器和滤光器中,能够直接影响太阳磁场望远镜偏光系统的测量精度[1]. 随着科技的进步,对于波片的精度要求越来越严格,所以对波片相位延迟的精密测量方法的研究具有重要意义.
波片相位延迟的测量,常见的测量方法有:电光调制法[2]、旋光法[3]、光谱扫描法、补偿法、光强测量法[4]、激光频率分裂法[5]、激光回馈法[6-7]、相位检测法[8]等. 以上测量方法的原理及技术都比较成熟,但有些方法的设备较为复杂且昂贵,有些方法要求对光强进行精准测量,有些方法对测量角度有着精准要求,故在实验过程中由于种种原因会引起较多的误差或由于实验器件的缺失无法进行测量. 本文设计了基于双声光光外差对光斜入射情况下波片相位延迟的测量系统,利用波片光轴在入射面不同方位时o光(寻常光)与e光(非常光)的传播特性来对波片的相位延迟进行检测,该方法使用的器件都是基础器件,对光强与测量角度没有严格要求,且该方法不仅仅限于1/4波片,还可应用于对各种波片的测量.
1 光外差检测技术
光外差检测有别于直接检测的检测技术,是利用光的相干性对光载波所携带的信息进行检测和处理,其检测原理与微波及无线电外差检测原理相似. 光外差检测与光直接检测比较,其测量精度要高7~8个数量级. 光外差检测具有很多重要优点,如测量速度快、抗干扰能力强及检测灵敏度可达到量子噪声限,其噪声等效功率可达10-20W,可以检测单个光子,进行光子计数. 但光外差检测对信号光和本振光的频率稳定性、偏振状态和空间相位有着非常严格的要求.
光外差检测系统利用光波的振幅、频率和相位携带信息,2束相干光入射到光探测器的光敏面进行混频,形成相干场,其原理如图1所示[9]. 图1中,νS为信号光束,νL为参考光束. 这2束平面平行的相干光,经过分光镜及聚光透镜入射到光电检测器的光敏面,在光敏面上进行叠加,形成相干光场.

图1 光外差测量系统原理图
2 实验原理
外差测量系统具有2束不同频率的光束,即参考光和信号光. 传统的光外差测量系统一般由声光调制器的0级光和1级光作为参考光与信号光,而双声光光外差测量系统的2束不同频率的光束是由2个驱动频率不同的声光调制器的1级光来提供[10].
如图2所示,光源为半导体激光器(型号为FC-630-030-SM)发出的光束经偏振分光棱镜PBS1后分成为2束偏振光,即p光与s光,其中p光为PBS1的透射光,s光为PBS1的反射光. p光经直角棱镜RAP1反射后与s光分别通过声光调制器AOM2与AOM1,微调AOM2与AOM1使得p光与s光以布拉格角通过,此时为1级衍射光最强. AOM1与AOM2为中国电子科技集团公司第26研究所生产的TSGMN-5型和TSGMN-3型声光调制器,其驱动频率分别为80 MHz与110.12 MHz. 通过光阑AD1与AD2将p光与s光的0级衍射光遮挡,使得最强的1级衍射光通过. s光的1级衍射光通过直角棱镜RAP2反射后与p光的1级衍射光在偏振分光棱镜PBS2处合光为1束正交光,这束正交光到达消偏振分光棱镜BS后分成2束正交光,一束透射,一束反射. 透射光经RAP3反射后经过检偏器AL1后在光电探测器PD1的光敏面上进行干涉, 同样反射光经过1/4波片再经RAP4反射后经检偏器AL2后在PD2的光敏面上进行干涉,两者都可转换为拍频30 MHz的电信号,此电信号可以通过示波器来观察,其中将CH1作为参考信号,CH2为测量信号,如图3所示.
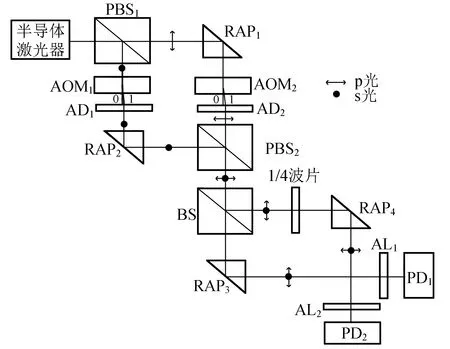
图2 双声光光外差测量系统
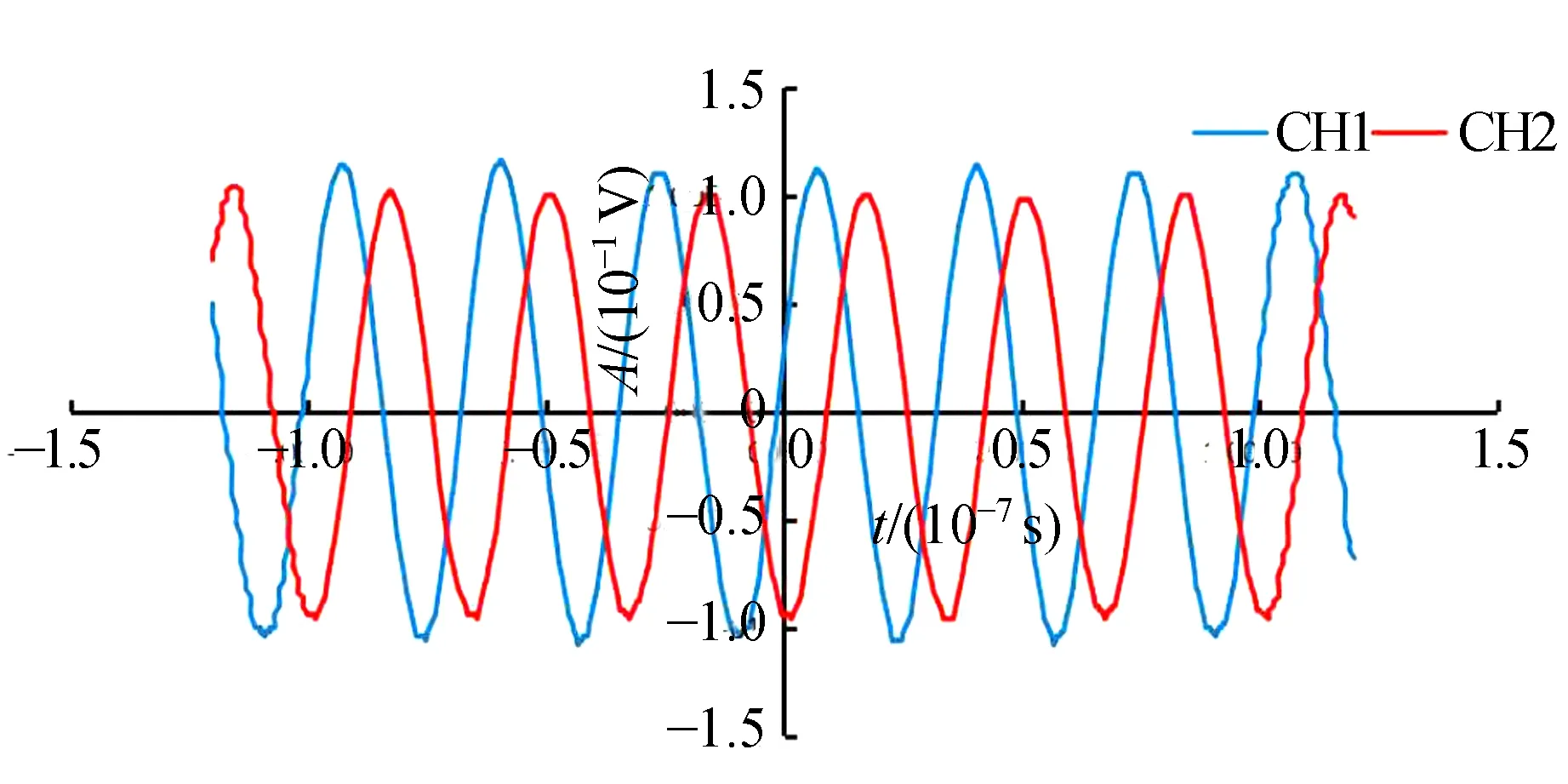
图3 30 MHz外差拍频信号
假设入射光经过声光调制器AOM1与AOM2后的1级衍射光的光强分别为Is和Ip,由图2可知,经过消偏振分光棱镜BS后的透射光束(即参考光束)中s光与p光的电场可分别表示为[11]
(1)
(2)
式中,ω0为激光束的角频率,ω1与ω2为声光调制器AOM1与AOM2的1级衍射光的移频,φ1和φ2为激光束在AOM1与AOM2的初相位,φ1r与φ2r为s光和p光的1级衍射光从AOM1和AOM2到光电检测器PD1的相位. 参考光束的s光与p光经检偏器AL1后在PD1的光敏面上进行干涉,并转换为电信号,该电信号为[12]
Ur∝cos (Δωt+Δφ+Δφr),
(3)
其中,Δω=ω1-ω2,Δφ=φ1-φ2,Δφr=φ1r-φ2r.
同理可得到经过BS的反射光束(即测量光束)的s光与p光的电场[11]为
(4)
(5)
式中φ1m和φ2m为s光和p光的1级衍射光从AOM1和AOM2到光电探测器PD2的相位. 测量光束的s光与p光经检偏器AL2后在PD2的光敏面上进行干涉,并转换为电信号,该电信号为[12]
Um∝cos (Δωt+Δφ+Δφm),
(6)
其中,Δφm=φ1m-φ2m.
为了减小误差,在测量过程中先将波片去除后将此时的状态作为初始状态,并将此时的数据记录并处理得到
δ0=Δφr-Δφm.
(7)
将δ0作为测量的初始相位,后在测量光路放置1/4波片,测量数据处理并计算可得到
δn=Δφrn-Δφmn,
(8)
Δδn=δn-δ0.
(9)
Δδn即为得到的测量结果.
3 测量方法
如图2所示,将波片置于双声光光外差测量系统的测量光路中,由于在实验过程中不能保证光线完全以0°入射波片,故通过以角度i来对波片的相位延迟进行推论. 本设计分别从光轴垂直于入射面和光轴平行于入射面2个方面来对波片的相位延迟进行验证.
3.1 光轴垂直于入射面,斜入射情况
如图4所示,以正晶体为例,波片厚度为d,s光与p光的合光以入射角i从空气进入波片. 波片光轴垂直入射面,此时o光光矢量与e光光矢量在入射面内的振动方向分别为平行于入射面和垂直于入射面. 由于p光与s光分别为平行于入射面和垂直于入射面的偏振光,在此时p光在e光光矢量上并没有分量,同理s光在o光光矢量方向上也没有分量,所以由o光出射的偏振光为p光,e光出射的偏振光为s光. 由惠更斯绘图法可以获得o光与e光的传播方向. 在这类的特殊情况下,o光与e光的传播方向都遵循普通折射定律.
入射平面波(波面位AA′)从波片表面A点入射,在波片中分解为o光和e光以不同折射角传播,分别至波片的另一面C和D点出射,出射光仍与入射光平行,这里对出射点D在该点o光与e光的存在光程差[13]. 故此时由D点出射的s光与p光存在相位差,为

(10)
此时的δ⊥即为式(9)中的Δδn.

图4 光轴垂直于入射面s光和p光在波片内的传播方向
记录不同角度下的相位差即可得到波片斜入射情况下的相位延迟.
3.2 光轴平行于入射面,斜入射情况
如图5所示,入射平行光从波片表面A点入射,经过一段时间在波片内o光与e光的波前位置,波片光轴平行入射面,此时e光光矢量与o光光矢量在入射面内的振动方向分别为平行于入射面和垂直于入射面. 由于p光与s光分别为平行于入射面和垂直于入射面的偏振光,在此时p光在o光光矢量上并没有分量,同理s光在e光光矢量方向上也没有分量,所以由e光出射的偏振光为p光,o光出射的偏振光为s光. 同上可知出射点D在该点时o光与e光存在光程差,由惠更斯绘图法与椭圆的解析几何理论可确定e光在晶体中的传播方向和波法线方向,求得e光在晶体中传播的折射率,并得到D点出射的s光与p光的相位差为

图5 光轴平行于入射面s光和p光在波片内的传播方向
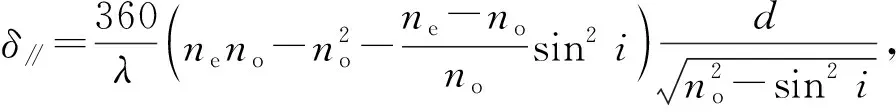
(11)
此时的δ∥即为式(9)中的Δδn.
记录不同角度下的相位差即可得到波片斜入射情况下的相位延迟.
4 测量结果与误差分析
使用的半导体激光器产生激光的波长为635 nm;波片为石英晶体多级波片,厚度为0.8 mm的1/4波片. 石英晶体为单轴正晶体,vo>ve,主折射率为no=1.544 3,ne=1.553 4.
分别对波片在光轴垂直于入射面和光轴平行于入射面的情况下进行入射角为0°的多次检测,通过示波器采集数据,最后通过Matlab软件处理数据. 测量误差如图6所示.

图6 测量误差
由图6可知,波片相位延迟的测量结果的误差范围在±2.67°.
将波片置于旋转平台上,测量波片不同角度的相位延迟. 通过对入射角在0°~15°范围内进行多次测量,对该方法做进一步的验证,通过示波器采集数据,并对数据进行处理得到实际值. 通过理论计算,可得到实验所用波片在2种情况下的0°~15°范围内相位延迟的理论数据,如图7~8所示. 旋转平台为ST201MR82B型号的精密手动旋转平台,台面可以360°旋转粗调,可以进行±10°的微细调整,测微头驱动,弹簧复位,分辨率高,无空回,精密轴系设计,轴系间隙可调,稳定性好,圆周360°刻划,方便读数.
由图7~8可知,实验数据与理论值基本一致,其中光线斜入射情况下当光轴垂直于入射面时波片的相位延迟为随着入射角度的增大而增大,光轴平行于入射面时波片的相位延迟随入射角度的增大而减小,该结果证明了本设计可以对波片的相位延迟进行处理.
由于实验装置并不能达到理想状态,使s光与p光的合光不能做到完美共线,导致参考光路与测量光路的对称性不能达到理想状态,这些都影响测量结果. 尤其是波片的放置问题,由于在本实验中光线并不能保证完全的打在波片的中心,且波片的光轴也不能确保与p光、s光的振动方向完全一致,尤其是波片的放置不能保证入射角一定为0°,由图7~8也可知入射角的变化也会对波片相位延迟的测量产生影响,如当入射角为1°时波片的相位延迟可增加0.5°,而实验时其入射角的偏转由于实验环境的影响有1°~3°的误差,导致相位延迟的最大误差在±2.37°,故该实验的测量精度可达到±0.5°.

图7 光轴垂直于入射面理论值与实验值

图8 光轴平行于入射面理论值与实验值
5 结 论
基于共线光外差测量系统测量了波片相位延迟,该方法的测量精度可达到±0.5°. 该方法对波片的测量具有实时性,且由于其可以分别通过对光轴垂直于入射面和光轴平行于入射面的2种检测来对检测结果进行验证. 在实验过程中发现当光垂直入射波片时,对波片进行360°的转动,参考信号与测量信号之间的相位差也会随之改变,且只有当光轴在入射面的垂直位置以及平行位置时,相位差的绝对值才会最大,故可通过该测量方法寻找波片的光轴方向.

