磁性斯格明子的旋性布朗运动研究

赵 乐，江万军

(清华大学 物理系，北京 100084)

磁性斯格明子是一种具有粒子特性的非共线自旋结构. 由于其拓扑属性的存在，许多新奇的拓扑量子输运现象，譬如拓扑霍尔效应、斯格明子霍尔效应等在斯格明子材料体系中都得到了广泛研究. 布朗运动是一种十分普遍的非平衡态热动力学现象，它描述的是热扰动下浸润在液体中微小颗粒的随机运动行为. 作为一种准粒子，磁性斯格明子在温度涨落时，同样会表现出随机运动的特性，但与其拓扑属性相关的热动力学行为却一直没有被发现. 本文介绍了实验室中对斯格明子热动力学行为的研究方法以及清华大学物理系江万军课题组近期在这一方向的研究进展，希望能够激发学生对于自旋电子学领域的研究兴趣，并为相关方向的研究提供一些方法与思路.

1 背景介绍与研究现状

1.1 布朗运动行为

布朗运动是指悬浮在流体(液体或气体)中的粒子在高速运动流体分子的碰撞下呈现出的随机运动行为(图1)，最早由苏格兰物理学家Robert Brown利用光学显微镜观察到，相关研究结果发表于1828年的《哲学》杂志上[1]. 1905年，根据分子动力学理论和扩散方程，爱因斯坦给出了布朗运动颗粒均方位移(Mean-squared Displacement,MSD)的表达式[2]

MSD(t*)=2dDdct*,

其中，d为运动的维数，Ddc为颗粒的扩散系数，t*

为用于计算MSD的统计间隔时间. 爱因斯坦还进一步指出，扩散系数Ddc应该是温度的线性函数，有

Ddc=μkBT,

其中，μ为颗粒的迁移率，kB为玻尔兹曼常量，T为热力学温度. 此关系式也得到了后续大量实验的验证.

图1 布朗运动颗粒的随机运动轨迹图[3]

1.2 磁性斯格明子

斯格明子(Skyrmion)一词来源于英国核物理学家Tony Skyrme于1962年在粒子物理领域提出的一种类似于独立粒子的拓扑稳定场结构[4]. 2009年德国慕尼黑工业大学Peter Böni课题组利用小角中子散射的方法在MnSi单晶块体材料中首次观测到了这种受拓扑保护的局域螺旋磁性结构[5]. 研究发现，相对于磁畴、磁泡等传统磁性结构，磁性斯格明子具有尺寸小、稳定性高、易于被电流操控等优点，因而引起了人们的高度关注与深入研究.

磁性斯格明子的拓扑属性是可以由拓扑电荷数来描述的，其表达式为

其中m为局域磁化强度方向上的单位矢量. 由于Q为m的奇函数，因此通过外加磁场，就可以改变磁化强度的方向，进而得到Q=+1和Q=-1的斯格明子(图2). 磁性斯格明子的拓扑电荷数始终为整数，而外界环境需要提供较多能量才可以破坏斯格明子的整体结构，这便是斯格明子拓扑保护的来源.

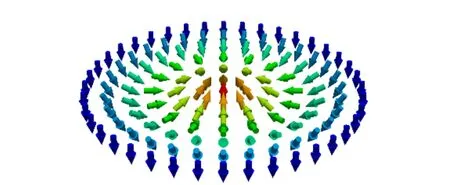
(a)Q=+1

(b)Q=-1图2 重金属-磁性薄膜材料体系中Q=+1与Q=-1奈尔型斯格明子示意图

拓扑电荷数相反(Q=±1)的磁性斯格明子在输运测量中会展现出相反的动力学行为，斯格明子霍尔效应就是其中非常典型的例子[6]. 如图3所示，在Ta/CoFeB/TaOx磁性多层膜中，通过施加横向(-x)方向的电流，利用磁光克尔效应显微镜成像技术，可以观测到Q=-1和Q=+1的斯格明子分别在纵向(-y与+y方向)发生偏转和堆积. 这种现象与电子和空穴的霍尔效应非常相似.

(a)Q=-1

(b)Q=+1图3 利用磁光克尔效应显微镜直接观察到磁性斯格明子的霍尔效应现象

1.3 磁性斯格明子热动力学行为的研究情况

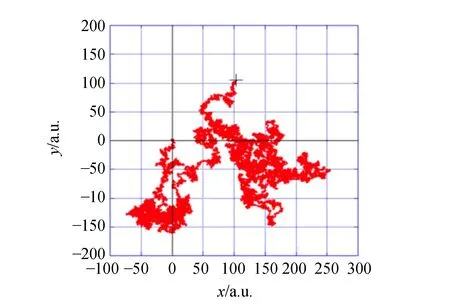
(a)数值模拟

(b)实验观测图4 数值模拟与实验观测得到的磁性斯格明子布朗运动轨迹图

磁性斯格明子热动力学的早期研究集中在理论推导与数值模拟方面[图4(a)][7-10]. 2019年，日本大阪大学Takayuki Nozaki等率先在W/FeB/Ir/MgO多层膜中观测到斯格明子在热扰动下的随机运动现象，并研究了垂直方向电场对斯格明子扩散系数的影响[11]. 德国美因茨大学Mathias Kläui课题组也随后研究了Ta/CoFeB/Ta/MgO/Ta体系中斯格明子的布朗运动行为，以及斯格明子扩散系数随温度的非线性变化关系[图4(b)][12]. 他们还指出，利用斯格明子的随机布朗运动行为，可以用来构建非常规计算单元. 但这些前期研究并没有就斯格明子的拓扑属性在热动力学行为中的表象进行深入讨论.

2 实验方法与研究思路

2.1 使用磁光克尔效应显微镜观察磁性斯格明子

磁光克尔效应(Magneto-optic Kerr Effect)是由苏格兰物理学家John Kerr于1877年发现的[13]，当1束线偏振光入射到磁化强度不为零的磁性样品表面并发生反射时，由于磁性样品对入射光p分量和s分量的反射率存在差异，故反射光的偏振方向会相对入射光转过一定角度，因此通过测量反射光偏振方向的改变就可以获知样品表面的磁矩指向.

利用磁光克尔效应显微镜，可以对样品表面不同位置的磁性信号进行实时观测，实现磁结构的空间分辨. 以德国Evico Magnetics公司生产的磁光克尔效应显微镜系统为例，该系统主要由光学显微镜、电磁铁、恒流源、样品托、LED灯组、CMOS相机和计算机等部分组成，系统光路图如图5所示. LED灯光通过光纤导入光学系统，在经过透镜组与光阑调制后，经过起偏器变为线偏振光并聚焦入射于样品表面，反射光在经过补偿器和检偏器后即可使用目镜进行观察或利用CMOS相机捕获并传输至计算机. 使用相配套的KerrLab控制与采集程序可以实现每秒近30帧的视频录制，这为研究磁性斯格明子的动力学提供了途径.

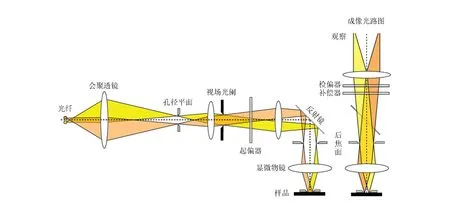
图5 Evico Magnetics公司生产的磁光克尔效应显微镜成像光路示意图[14]

2.2 利用ImageJ软件获取磁性斯格明子的位置信息

利用ImageJ软件可以对使用KerrLab程序录制的视频进行后期处理与分析. ImageJ是基于Java的多平台公共图像处理软件[15]，拥有大量官方和第三方插件，为基于图片分析的科学研究提供了极大方便. 本研究中，利用由M.B. Smith等开发的Speckle TrackerJ插件[16]，对视频中的运动物体进行自动追踪并获取物体在每帧图片上的坐标信息，同时将数据导出为文本文件进行后续计算和处理. 如图6所示，首先使用ImageJ对采集到的原始视频图像进行反色与提高对比度操作，接下来进行高斯模糊，可以发现图像中的背景噪声被基本消除，且斯格明子图像边缘平滑、辨识度增强. 最后使用Speckle TrackerJ插件对斯格明子位置进行追踪，即可得到其随时间变化的位置数据.

(a)原始图像

(b)进行反色、提高对比度

(c)高斯模糊图6 使用ImageJ软件对图像进行处理

2.3 计算均方位移与扩散系数

通过计算均方位移，可以非常直观地反映热运动颗粒的扩散行为. 对于二维运动，均方位移的表达式为

MSD(t*)=〈Δr2(t*)〉=

〈Δx2(t*)+Δy2(t*)〉=

[y(iΔt+t*)-y(iΔt)]2}=4Ddct*,

其中，Δt为位置数据的时间分辨率，t*为统计间隔时间，即对于不同的统计间隔时间会得到不同的均方位移. 理论上均方位移与统计间隔时间之间满足较好的线性关系，通过线性拟合得到斜率即可计算出运动颗粒扩散系数Ddc的大小.

3 实验进展

3.1 观察单个磁性斯格明子的随机热运动行为

首先使用超高真空磁控溅射设备生长了具有磁性斯格明子的Ta(5 nm)/Co20Fe60B20(1 nm)/TaOx(3 nm)3层膜结构[17]. 为了消除各向异性形状限制的影响，进一步使用微加工技术将样品制备为圆形器件，如图7所示. 接下来使用磁光克尔效应显微镜观察样品表面的磁畴结构，在略高于室温的环境中(320.6 K)，可以观察到单个斯格明子受到热扰动而呈现出随机运动的行为. 录制视频并使用ImageJ进行处理，即可得到单个斯格明子的运动轨迹图，如图8(a)所示. 利用不同时刻的位置数据，可以计算得到斯格明子不同时刻的扩散速度大小，斯格明子的扩散速度在x方向和y方向都以0为中心随机分布，如图8(b)和(c)所示. 通过对扩散速度大小进行统计，发现斯格明子的扩散速度分布服从高斯分布，如图8(d)和(e)所示，这与经典的布朗运动特征一致.

图7 样品显微图

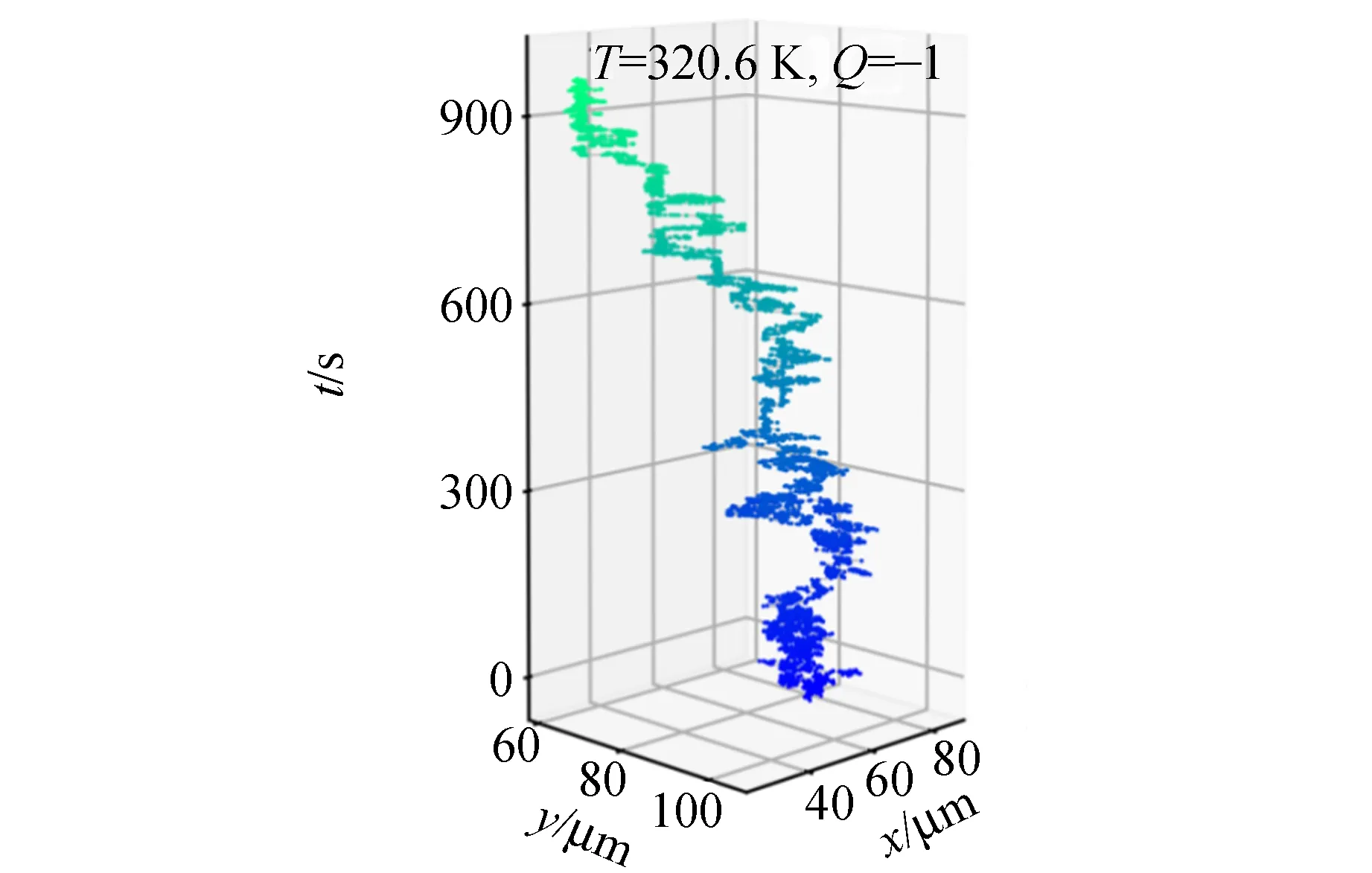
(a)运动轨迹图

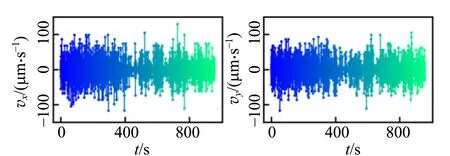
(b)x方向扩散速度 (c)y方向扩散速度

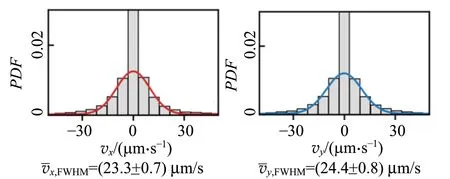
(d)x方向速度分布 (e)y方向速度分布图8 温度为320.6K时磁性斯格明子随机热运动行为的实验测量结果

3.2 斯格明子热运动行为随温度的变化

使用与磁光克尔效应显微镜配套的变温样品托，研究了温度对斯格明子热运动行为的影响，如图9(a)～(c)所示. 当温度升高时，斯格明子的热运动现象会变得更加剧烈. 通过计算均方位移，可以对不同温度下的扩散行为进行定量描述，如图9(d)所示. 在不同温度下，均方位移与统计间隔时间均表现出良好的线性关系. 通过线性拟合，可以得到不同温度下斯格明子运动的扩散系数，如图9(e)所示. 可以看出，随着温度的增加，扩散系数呈现出非线性的上升行为，这与爱因斯坦的线性温度相关扩散理论存在差异. 我们认为这一非线性行为来源于样品中随机分布的缺陷对斯格明子运动的钉扎作用，而使用将爱因斯坦的线性温度扩散关系与描述从缺陷中热激发的Arrhenius形式函数相乘所得到的表达式

可对这一非线性行为进行较好的拟合，如图9(e)中的绿色曲线所示. 从拟合参量还可以得知样品中缺陷的平均钉扎势Ep约为8.2 meV，而斯格明子热运动的激活温度T0约为305.3 K，即只有当环境温度高于温度T0，斯格明子才有较大机会从缺陷中逃逸，进而表现出随机热运动的行为.

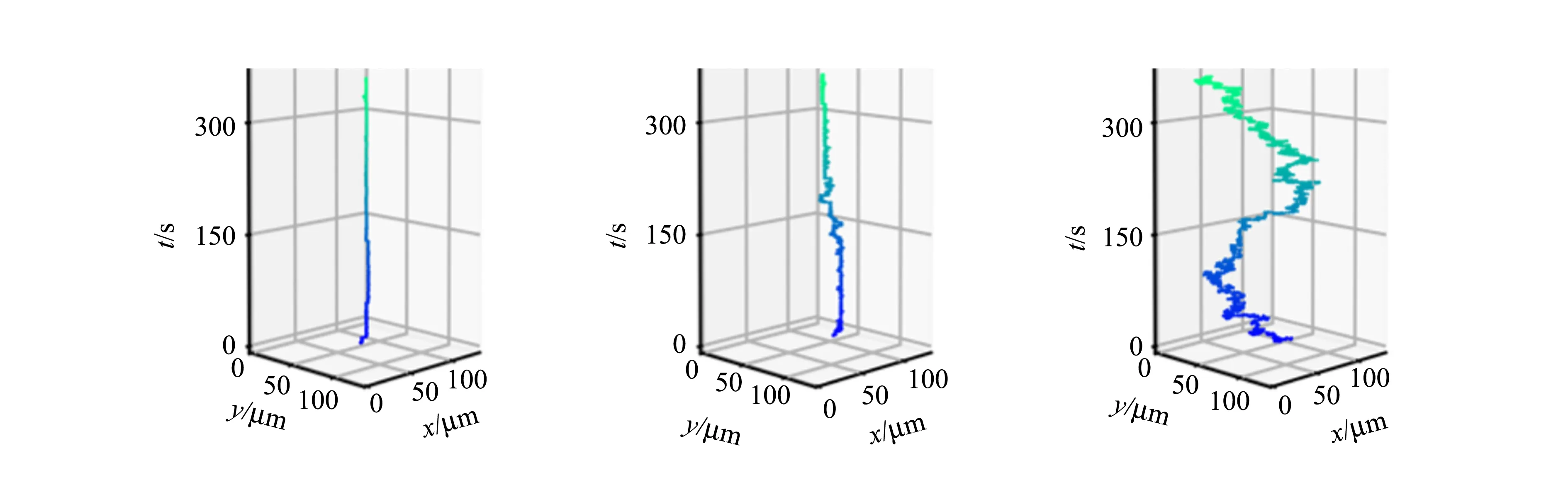
(a)T=306.3 K (b)T=314.9 K (c)T=326.5 K

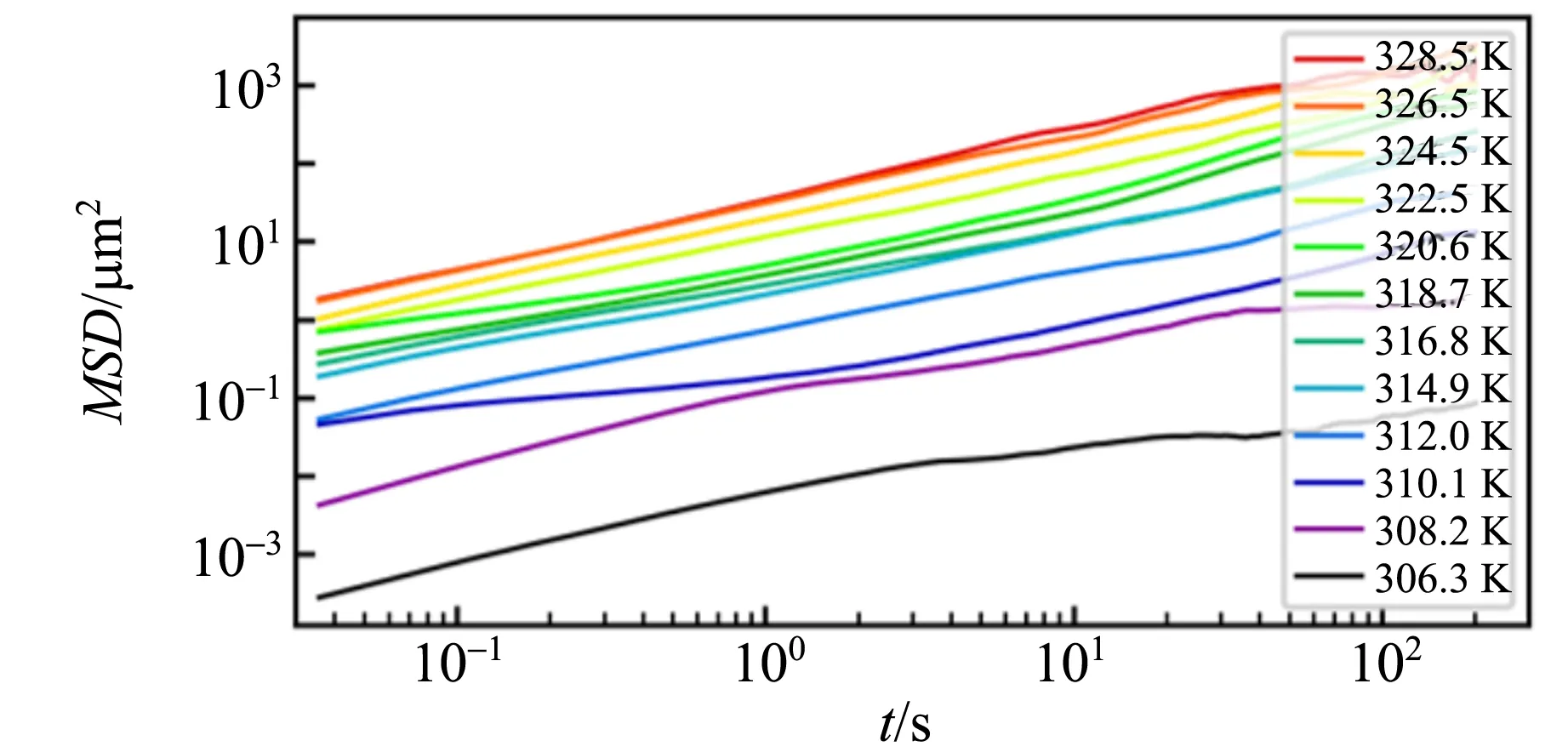
(d)不同温度的扩散行为

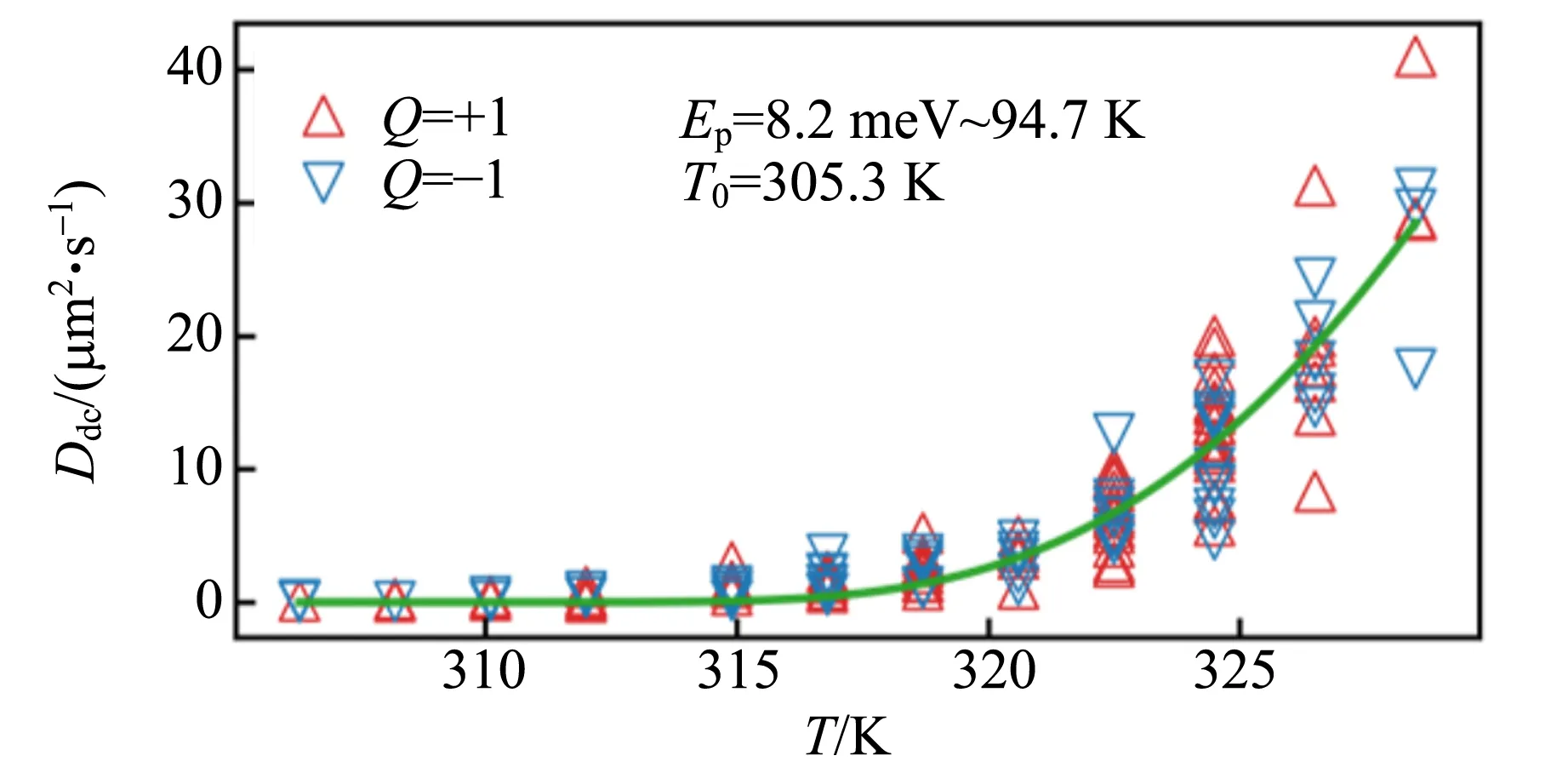
(e)不同温度下斯格明子运动的扩散参量

图9 斯格明子的热运动行为随温度的变化关系

3.3 斯格明子旋性布朗运动的实验验证

为了研究斯格明子拓扑相关的旋性热动力学行为，定义了斯格明子旋转角θsr，它描述的是斯格明子运动过程中相邻时间间隔速度矢量的夹角，如图10所示. 根据随机Thiele方程

可以计算得到斯格明子旋转角的表达式为

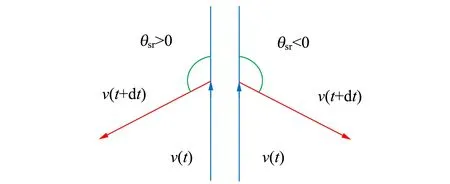
图10 斯格明子旋转角示意图

由此可以看出，斯格明子旋转角θsr是与拓扑电荷数Q直接相关的. 基于随机LLG方程的微磁学模拟表明，Q=+1和Q=-1的斯格明子在做布朗运动的同时会分别向顺时针和逆时针方向旋进，如图11(a)和(b)所示. 通过计算斯格明子旋转角θsr，可以非常明显地看到Q=+1的斯格明子具有小于0的斯格明子旋转角，而Q=-1的斯格明子具有大于0的斯格明子旋转角，如图11(c)所示. 通过分析实验中采集到的斯格明子位置信息与速度信息，也可以得到相同的现象. 如图11(d)和(f)所示，Q=+1的斯格明子旋转角为负，对应于顺时针旋进行为；而Q=-1的斯格明子旋转角为正，对应于逆时针旋进行为. 这证明在实验中确实观测到了单个磁性斯格明子的旋性布朗运动现象.

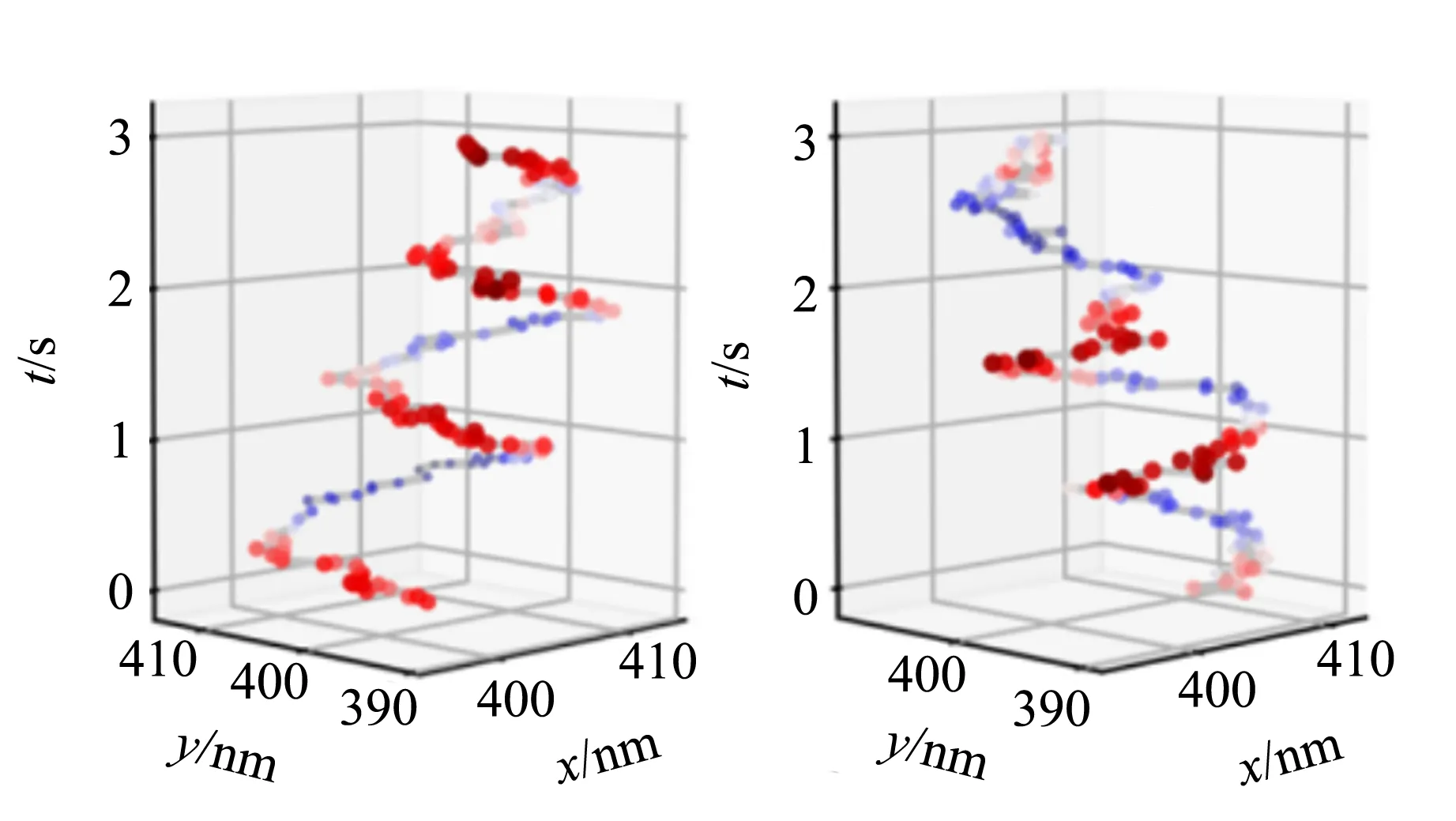
(a)Q=+1(模拟) (b)Q=-1(模拟)

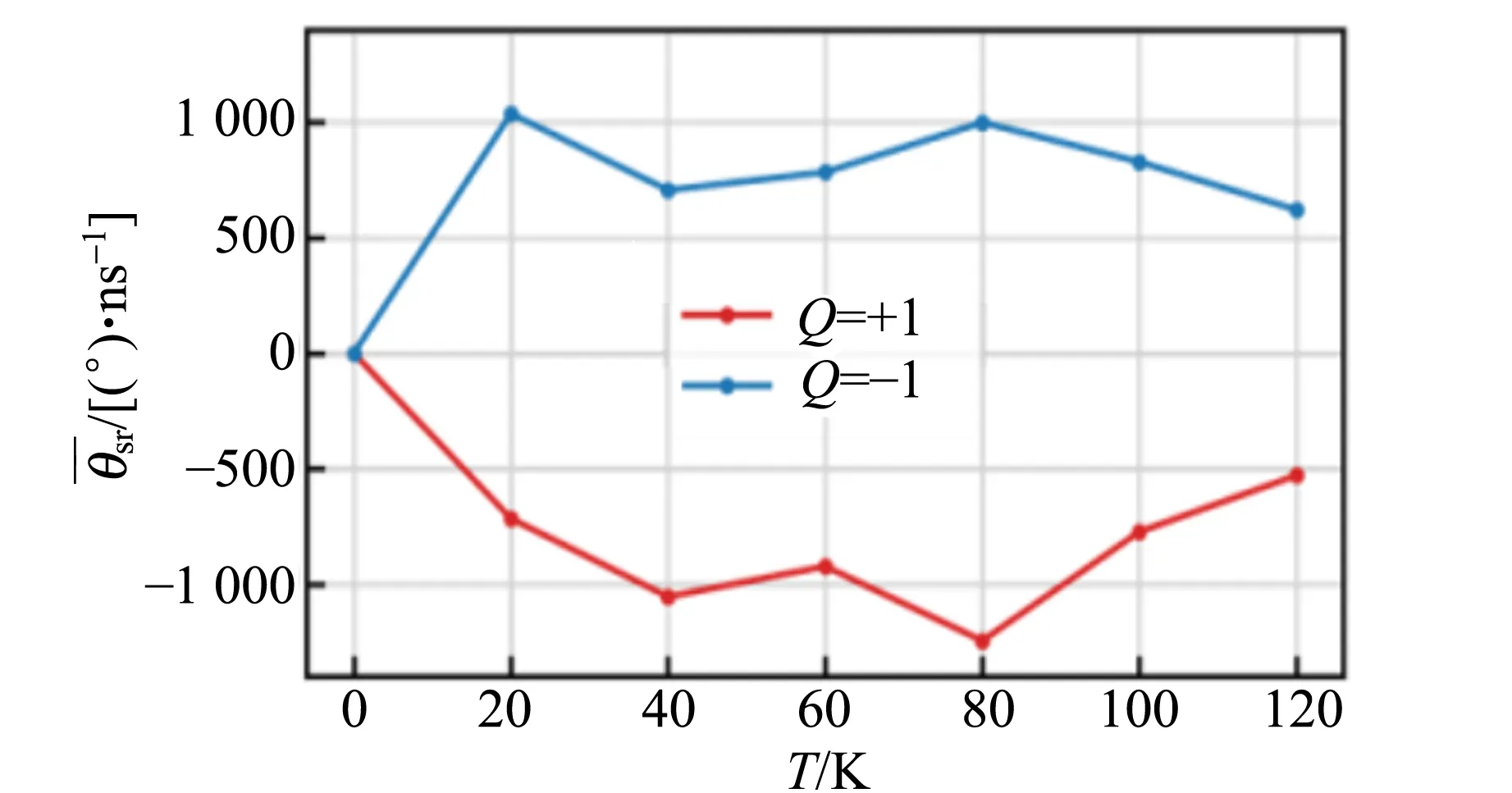
(c)θsr与T的关系(模拟)

(d)Q=+1(实测) (e)Q=-1(实测)

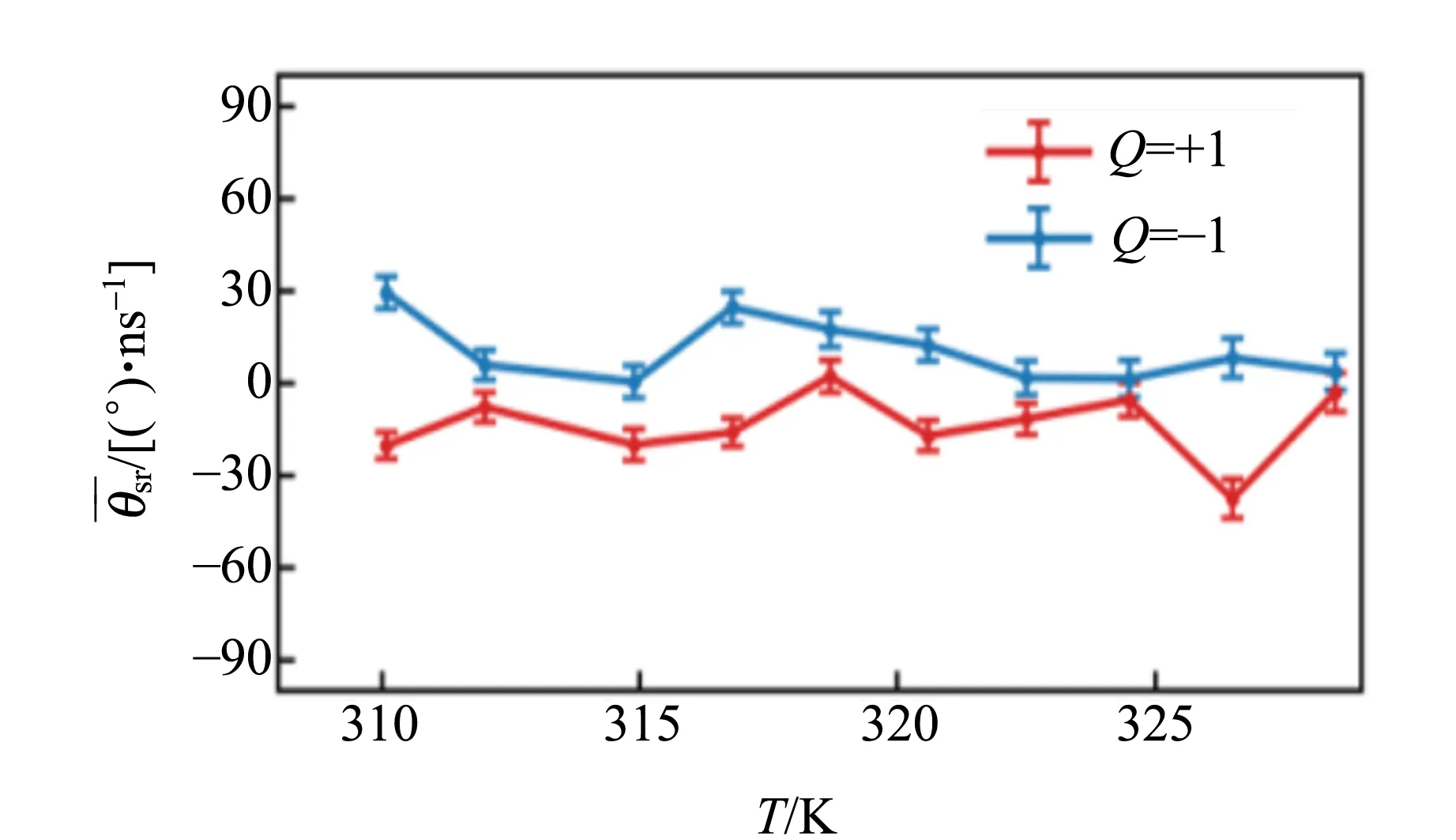
(f)θsr与T的关系(实测)图11 斯格明子旋性布朗运动的数值模拟与实验观测结果

4 结束语

简述了布朗运动和磁性斯格明子的基本知识以及磁性斯格明子的相关实验研究进展，进一步介绍了单个斯格明子的布朗运动现象，包括其随温度非线性增加的扩散系数以及与拓扑相关的旋性运动行为. 磁性斯格明子是一种潜在的信息存储单元，在未来自旋电子学器件中可能会发挥重要的作用，斯格明子拓扑相关热运动行为也为器件设计与应用提供了更多可能性.