用双臂电桥测金属丝杨氏模量的优化实验*

刘志亮

(青海大学机械工程学院　青海 西宁　810016)

1　引言

杨氏模量是衡量材料受力之后抵抗变形能力的一个物理量，在工程技术设计中进行材料的选择时，该量是一个十分常用且重要的参数，因而对于材料杨氏模量的精确测量具有非常重要的意义．在大学物理实验中，通常采用光杠杆法和百分表法来测量金属丝的杨氏模量，以上方法不但操作繁琐，而且精度较低[1,2]．文献[3]利用双臂电桥通过对微小电阻的测量算出了金属丝的杨氏模量，此法虽操作相对简单、精度有所提高，但所用公式较为复杂，测量的量较多．

本文在该实验的基础上，通过对公式的进一步推导，得出一个用双臂电桥测金属丝杨氏模量更加简单、精确的新公式，从而使此方法更加完善．

2　实验原理及设备

2.1　实验原理

由胡克定律知，在弹性限度范围内，金属丝在拉力作用下发生的形变满足如下公式

(1)

式(1)中，E即为我们想要测量的杨氏模量，F为施加在金属丝上的轴向拉力，L为实验过程中金属丝接入电桥的长度，S为金属丝的横截面积，ΔL表示在施加拉力F前后，金属丝的长度变化量．然而，金属丝长度的变化量与电阻的变化量又存在如下关系

(2)

式(2)中ΔR为金属丝电阻的变化量，ρ为金属丝的电阻率，将式(2)通过变形，代入式(1)中，最终得到

(3)

式(3)即为文献[3]用双臂电桥测金属杨氏模量的理论公式．由上式可以看出，若要测出金属丝的杨氏模量，除了测量金属丝电阻的电阻和横截面积，还必须需查得该类金属的电阻率，而实际使用金属丝的电阻率可能与理论值存在一定的偏差，同时还需测量接入双臂电桥中金属丝的长度，对于其长度的测量一般采用米尺，因而测量精度不高．

由电阻的决定式可知：同一材料的电阻与材料的长度成正相关，与材料的横截面积成负相关，即

(4)

式(3)中，ρ表示金属丝的电阻率，L表示金属丝接入电桥的原始长度，所以金属丝接入电桥时的原始电阻R0满足如下式子

(5)

将式(5)代入式(3)中有

(6)

通过对金属丝直径d的测量即可得出其横截面积，代入横截面积

(7)

式(7)即为本实验优化后的理论测量公式，由式(7)中我们可以看出，该实验仅需测量金属丝的电阻和横截面积即可，横截面积可通过螺旋测微仪精确测量，而金属丝的微小电阻也可通过双臂电桥精确测量得到，相比于原实验，引入和测量的量减少，实验精度进一步提高，实验更加简单方便．

2.2　实验仪器及装置

该实验用到的主要仪器设备有：悬挂金属丝的铁架台，质量为1 kg的砝码 ，待测金属丝 ，螺旋测微仪，QJ44型直流双臂电桥．实验装置图如图1所示，为了保证实验的精度，我们将悬挂金属丝的夹具进行了如图1中A处的防滑和绝缘处理．

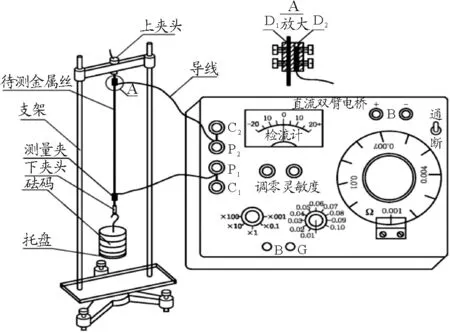
图1　用双臂电桥测金属丝杨氏模量的优化实验装置图

3　实验步骤

(1)先对支架悬挂金属丝的旋钮用绝缘胶带缠绕以绝缘，同时加以防滑，将金属丝一端固定在支架旋钮上，将悬挂砝码的挂钩用绝缘胶带缠绕以绝缘，用螺旋测微仪测量金属丝的直径d(分别在金属丝的上中下部选择5段进行测量)．

(2)将金属丝选择合适长度运用四端接法接入双臂电桥[4]，其中电流端C1和C2接金属丝外侧，电压端P1和P2接金属丝内侧．

(3)打开电桥电源开关，使仪器预热5 min，将灵敏度调至最低挡，旋动调零旋钮对双臂电桥进行调零．

(4)先按下双臂电桥的B按钮，间隔10 s，再按下G按钮，调节电阻使指针在零附近，调节灵敏度至最高，再调节电阻使检流计指向零，读出电桥板面上电阻的值即为金属丝接入电桥的电阻R0．

(5)加挂1 kg的砝码等8～10 min后，打开双臂电桥开关后重复步骤4测出伸长后接入电桥金属丝的电阻Ri．

(6)重复步骤5测量6次，每次增加砝码1 kg，记录数据．

4　数据处理及误差分析

4.1　数据处理

通过以上实验步骤，测量并记录相关实验数据，表1为增加砝码时接入电桥金属丝的电阻值，表2为用螺旋测微仪测量金属丝所得的直径．

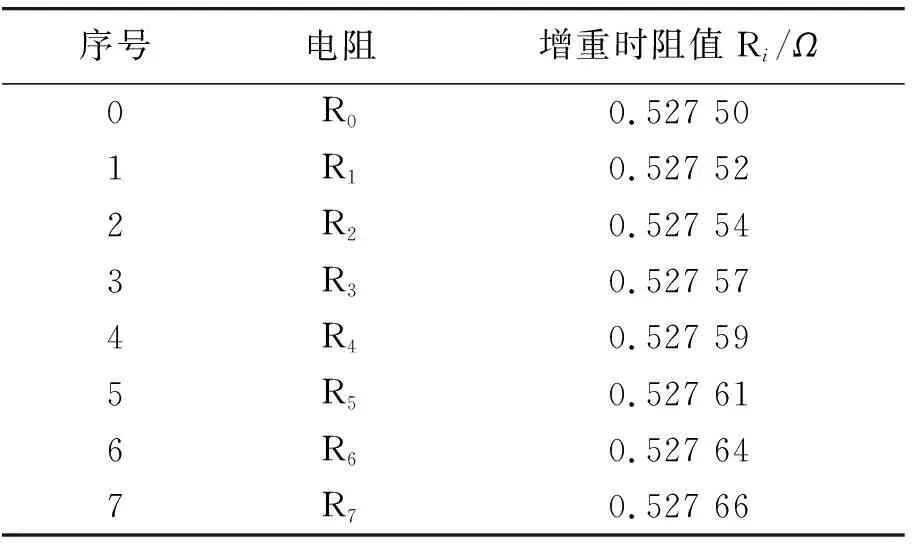
表1　悬挂不同砝码时接入电桥金属丝的电阻

表2　金属丝的直径

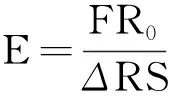
(8)

对表1数据进行线性拟合，处理过程如表3所示.

表3　线性拟合处理过程

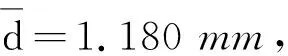
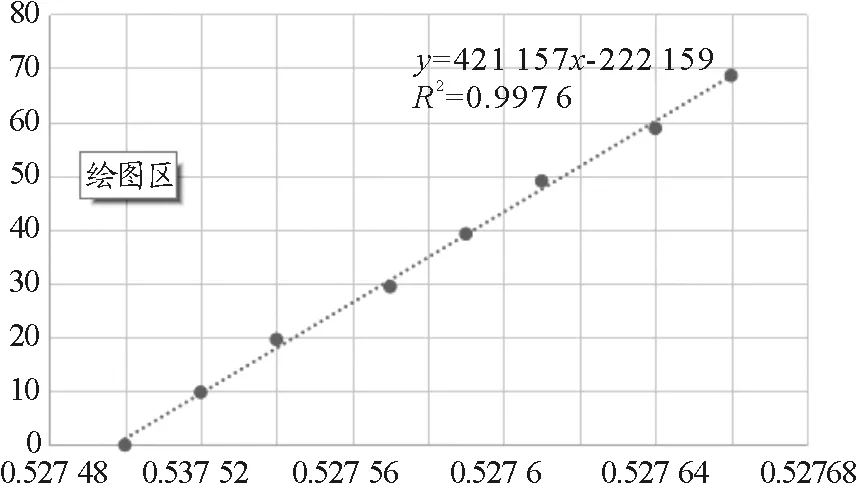
图2　悬挂不同砝码时接入电桥金属丝的电阻

4.2　误差分析

(1)实验所悬挂的砝码，部分被锈蚀导致质量不足1 kg，可能引起一定误差．

(2)在对金属丝电阻的测量时，金属丝伸长可能未达到稳定状态导致所测量的电阻不准，从而引

起误差．

(3)将金属丝接入双臂电桥时，由于有接触电阻的产生[5]，造成测量电阻与实际电阻存在偏差，因而引起实验误差．

5　结语

本实验通过对原有公式的合理推导，得出一个更加简单的测量公式，减少了实验需要测量和引入的量，精度得到了有效提升，从而使利用双臂电桥测量杨氏模量的实验进一步优化．

TheOptimizedExperimentofMeasuringtheYoung’sModulusofMetalWirewithDoubleBridge

Liu Zhiliang

(School of Mechanical Engineering,Qinghai University,Xining,Qinghai810016)

Abstract:The wire under the action of tension will occur along the axial small deformation, thus caused the wire resistance small changes, Ma Yuli etc through to the resistance measurement to calculate the young's modulus of metal wire, this experiment based on this, through the formula is derived, it is concluded that a more simple formula, decrease the measurement, further improve the accuracy.

Keywords:double Bridge;Young's modulus;small deformation;resistance