三角形中考综合考点追踪

文 周斌

三角形在中考中的考点，从内部来看，包括等腰三角形、直角三角形以及与三角形有关的线段；从外部来看，包括三角形的全等、相似以及三角形与其他图形的关系。在中考中，三角形往往与这些知识结合在一起考查。

一、三角形与四边形

例1（2020·甘肃天水）如图1，在边长为6的正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，将△ADF绕点A顺时针旋转90°得到△ABG，若DF=3，则BE的长为_______。

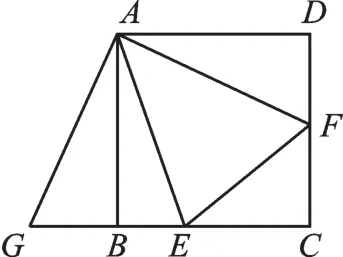
图1

【分析】根据旋转的性质可得AG=AF，GB=DF，∠BAG=∠DAF，然后根据正方形的性质和等量代换可得∠GAE=∠FAE，进而可根据SAS证明△GAE≌△FAE，可得GE=EF。设BE=x，则CE与EF可用含x的代数式表示，然后在Rt△ECF中，由勾股定理可得关于x的方程，解方程即得答案。

解：∵将△ADF绕点A顺时针旋转90°得到△ABG，

∴AG=AF，GB=DF，∠BAG=∠DAF，

∵∠EAF=45°，∠BAD=90°，

∴∠BAE+∠DAF=45°，

∴∠BAE+∠BAG=45°，

即∠GAE=45°，

∴∠GAE=∠FAE。

又∵AE=AE，AG=AF，

∴△GAE≌△FAE（SAS），

∴GE=EF。

设BE=x，则CE=6-x，

EF=GE=DF+BE=3+x。

∵DF=3，∴CF=3。

在Rt△ECF中，由勾股定理，得

CE2+FC2=EF2，

即（6-x）2+32=（x+3）2，

解得x=2，

即BE=2。

故答案为2。

【点评】本题考查了旋转的性质、正方形的性质、全等三角形的判定和性质以及勾股定理等知识，属于常考题型。熟练掌握上述基本知识、灵活应用方程思想是解题的关键。

二、三角形与圆

例2（2020·贵州安顺）如图2，△ABC是⊙O的内接正三角形，点O是圆心，点D、E分别在边AC、AB上，若DA=EB，则∠DOE的度数是_______度。

图2

【分析】本题可通过构造辅助线，利用垂径定理证明角相等，继而利用SAS证明三角形全等，最后根据角的互换，结合同弧所对的圆周角等于圆心角的一半求解。

解：连接OA、OB，作OH⊥AC、OM⊥AB，垂足分别为H、M，如图3所示。

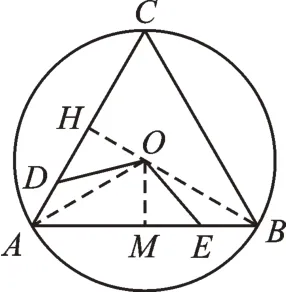
图3

∵在等边三角形ABC中，OH⊥AC，OM⊥AB，

由垂径定理，得AH=AM。

又∵OA=OA，

∴△OAH≌△OAM（HL），

∴∠OAH=∠OAM。

∵OA=OB，

∴∠OAB=∠OBA，

∴∠OAD=∠OBE。

又∵AD=EB，

∴△ODA≌△OEB（SAS），

∴∠DOA=∠EOB，

∴∠DOE=∠DOA+∠AOE=∠AOE+∠EOB=∠AOB。

又∵∠C=60°，

∴∠AOB=120°。

即∠DOE=120°。

故答案为120。

【点评】本题考查了圆与等边三角形的综合运用，需要根据等角的互换将所求问题进行转化。构造辅助线是本题的难点。全等以及垂径定理的应用在圆的综合题中极为常见，圆心角、弧、圆周角的相互关系需熟练掌握。