以教材为本，“浮想联翩”来解题

文 祁勇程坤

三角形的全等是初中几何的基础和重点，在近几年的中考中所占分值也越来越高，但很多同学在解题时找不到题目中的全等三角形，给解题带来一定的障碍。如何才能对全等特别“敏感”，像条件反射似的“一眼看中”呢？这就需要我们发挥教材例题的作用，学会“浮想联翩”。

原题呈现（苏科版数学教材八年级上册第21页例6）如图1，点A、B、C、D在一条直线上，EA∥FB，EC∥FD，EA=FB。求证：AB=CD。

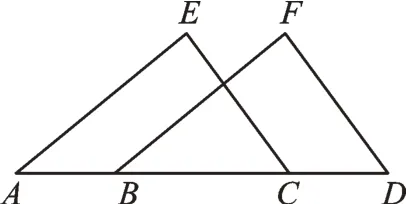
图1

【分析】要证AB=CD，只要证AB+BC=CD+BC，即AC=BD，所以只要证△EAC≌△FBD。根据已知条件再去寻找全等的条件，从而通过“角角边”证明两个三角形全等。

证明：∵EA∥FB，EC∥FD，

∴∠A=∠FBD，∠ECA=∠D。

又∵EA=FB，

∴△EAC≌△FBD（AAS），

∴AC=BD，

即AB+BC=CD+BC，

∴AB=CD。

【点评】要证明线段相等，先证明三角形全等是常用的方法。

一、条件和结论互换

变式1如图1，点A、B、C、D在一条直线上，EA∥FB，EC∥FD，AB=CD。求证：EA=FB。

【分析】要证EA=FB，只要证△EAC≌△FBD，从而去寻找证明两个三角形全等的条件。最终可由“角边角”证明全等。

证明：∵EA∥FB，EC∥FD，

∴∠A=∠FBD，∠ECA=∠D。

∵AB=CD，

∴AB+BC=CD+BC，

即AC=BD，

∴△EAC≌△FBD（ASA），

∴EA=FB。

【点评】将教材原题中的条件和结论互换，仍然是围绕三角形全等来解决线段相等问题。

变式2如图1，点A、B、C、D在一条直线上，EA∥FB，EA=FB，AB=CD。求证：EC∥FD。

【分析】要证EC∥FD，只要证∠ECA=∠D，从而想到证明△EAC≌△FBD。

证明：∵EA∥FB，

∴∠A=∠FBD。

∵AB=CD，

∴AB+BC=CD+BC，

即AC=BD。

又∵EA=FB，

∴△EAC≌△FBD（SAS），

∴∠ECA=∠D，

∴EC∥FD。

【点评】还是将教材原题中的条件和结论互换，将证明线段平行转化成证明角相等。证明三角形全等也是解决角相等的常用手段。

二、图形的变换

变式3如图2，∠ACB=∠ECF，AC=BC，EC=FC。求证：AE=BF。

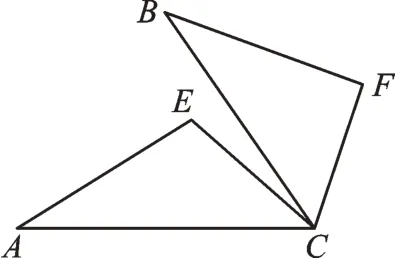
图2

【分析】要证AE=BF，只要证明△ACE≌△BCF。

证明：∵∠ACB=∠ECF，

∴∠ACB-∠ECB=∠ECF-∠ECB，

即∠ACE=∠BCF。

又∵AC=BC，EC=FC，

∴△EAC≌△FBC（SAS），

∴AE=BF。

【点评】如果教材原题中的图是将△ACE沿AC向右平移一定的距离得到的，那么此题的图就是将△ACE绕点C旋转一定的角度得到的。此题还是围绕全等三角形来解决。

变式4如图3，AC⊥BC，DC⊥EC，AC=BC，DC=EC，图中AE、BD有怎样的大小和位置关系？试证明你的结论。

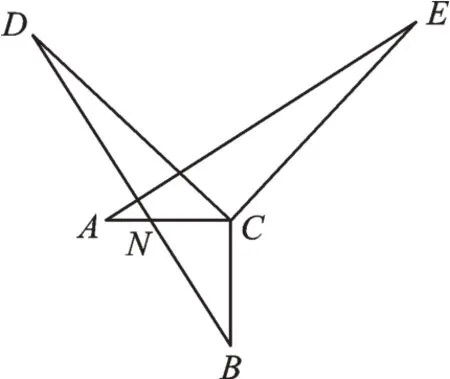
图3

【分析】根据SAS即可求得△DCB≌△ECA，求得∠B=∠A。又因为∠AND=∠BNC，再根据三角形的内角和定理即可求得∠A+∠AND=90°，从而证得BD⊥AE。

解：AE=BD，AE⊥BD。

证明如下：

∵∠ACB=∠DCE=90°，∠ACD=∠ACD，

∴∠DCB=∠ECA。

在△DCB和△ECA中，

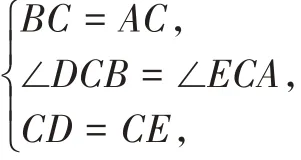
∴△DCB≌△ECA（SAS），

∴∠A=∠B，BD=AE。

∵∠AND=∠BNC，∠B+∠BNC=90°，

∴∠A+∠AND=90°，

∴AE⊥BD。

【点评】本题主要考查全等三角形的判定，利用全等三角形得出线段相等和角相等是解题的关键。证明三角形全等的基本思路是：

1.已知有两个角对应相等，证它们任意一边对应相等；

2.已知有两边对应相等，证它们的夹角相等，或证第三边相等；

3.已知有一角和一边对应相等，证夹等角的另一边相等或证另一角相等；

4.已知有一角和其对边对应相等，证另一角对应相等。

我们在做证明题时，首先要认真审题，弄清已知条件，看已知条件符合基本思路的哪种情况，再寻求解题途径。