导线接续管钢套对放线滑车的冲击计算方法及接触过程分析*

秦 剑，万建成，贾 宁，刘 晨

(中国电力科学研究院有限公司，北京 100055)

0 引言

输电线路工程导线张力放线施工中，需要将不同线盘的导线通过接续管压接后连成整根，在牵引机的带动下通过挂在铁塔上的放线滑车。由于接续管为强度较低的铝材，不能承受较大的弯曲，因此需要在接续管外安装钢套进行保护[1-2]。

随着特高压工程建设中导线截面积不断增大，接续管钢套的直径及长度随之增加。在放线过程中钢套通过滑车时，其端部与滑车产生冲击作用力，不但对滑车结构安全有影响，而且钢套与滑车接触力过大时，易发生接续管变形、导线弯折等损伤，产生安全风险。

目前，导线接续管钢套过滑车连续过程尚未开展深入研究，钢套的设计载荷仅采用钢套中部在滑车上的静力载荷，即未考虑钢套端部对滑车的碰撞力，亦未考虑通过滑车过程中滑车前后摆动对钢套的影响，而冲击分析是工器具结构精细化设计的关键环节[3]，因此应以多结构体接触动力计算方法为基础开展研究。

在多体系统碰撞计算中主要采用冲量-动量法、罚函数法和附加约束法[4]。冲量-动量法以刚体假设为基础，把碰撞看成瞬时动力学过程[5]。罚函数法是连续碰撞力模型，用弹簧-阻尼力元来代替碰撞力，不增加动力学方程的维数，因此在柔性多体领域和有限元领域都得到广泛应用[6]。但罚函数法的碰撞力模型及刚度系数等参数往往依赖经验进行选择，使得结果不够稳定、可靠。另外，罚函数法所假设的嵌入量不符合碰撞物体互不穿透的物理实际。附加约束法将接触作用看作约束，以接触对之间互不穿透为约束条件引入动力学方程进行求解，能更准确描述物理实际[7]。

有限质点法是近年来发展起来的结构分析数值计算方法，该方法将结构离散为相互联系的质点集合，质点间通过单元连接，并以质点的运动来描述结构行为，结构静、动力问题均采用运动方程求解，在处理结构大变形、接触、碰撞等非线性问题方面取得良好的应用效果[8-10]。俞锋等[11]对索与滑轮接触进行分析；秦剑等[12]对索道载荷过鞍座冲击的影响进行深入计算；张鹏飞[13]针对杆、板等结构提出接触力的简化计算方法。

本文在有限质点法的基础上提出导线接续管钢套通过放线滑车过程的冲击动力计算方法，采用接触约束方法计算接触力，获得稳定的计算结果，并针对施工中出现的多种因素对导线接续管钢套及滑车运动系统进行计算分析。

1 接续管钢套过滑车运动系统

在输电线路张力放线过程中，当一盘导线展放完后需更换新的导线，并通过铝制接续管将2根导线连接，接续管外安装保护用钢套，以保证接续管通过放线滑车时不发生弯曲变形。

在牵引机的牵引力及张力机的张力作用下，导线、接续管及钢套连续通过线路中多个放线滑车。在这个过程中，牵引侧导线、钢套、张力侧导线及滑车、滑车悬臂可看作由平面内多个部件组成的多体运动系统。

1.1 多体系统位置

放线滑车悬挂在铁塔横担上，悬挂点S为固定点。以S为原点建立坐标系，钢套过滑车运动系统如图1所示。

图1 接续管钢套过滑车运动系统Fig.1 Motion system of steel sleeve of connecting pipe passing through pulley

牵引侧导线(AB)、钢套(BC)、张力侧导线(CD)依次通过滑车，滑车中心为O。放线滑车在悬臂的作用下绕悬挂点S发生前后摆动。牵引方向及张力方向由放线工况确定，在钢套过滑车过程中保持不变。θ，Φ，ω分别为牵引角度、张力角度、摆动角度。

在牵引力与张力的作用下，将导线视为柔性的线弹性单元，仅承受单向拉力，且不产生弯曲变形，运动过程中弹性模量及截面积保持不变。

1.2 导线、钢套与滑车的接触

导线、钢套分别与滑车发生接触，且接触类型各不相同，进行分别讨论。

1)导线与滑车的柔性接触

在牵引力与张力的作用下，导线与滑车接触的部分与滑车完全贴合，不接触的部分为直线。

按以下2种情况讨论导线与滑车的接触。导线与滑车接触情况如图2所示。

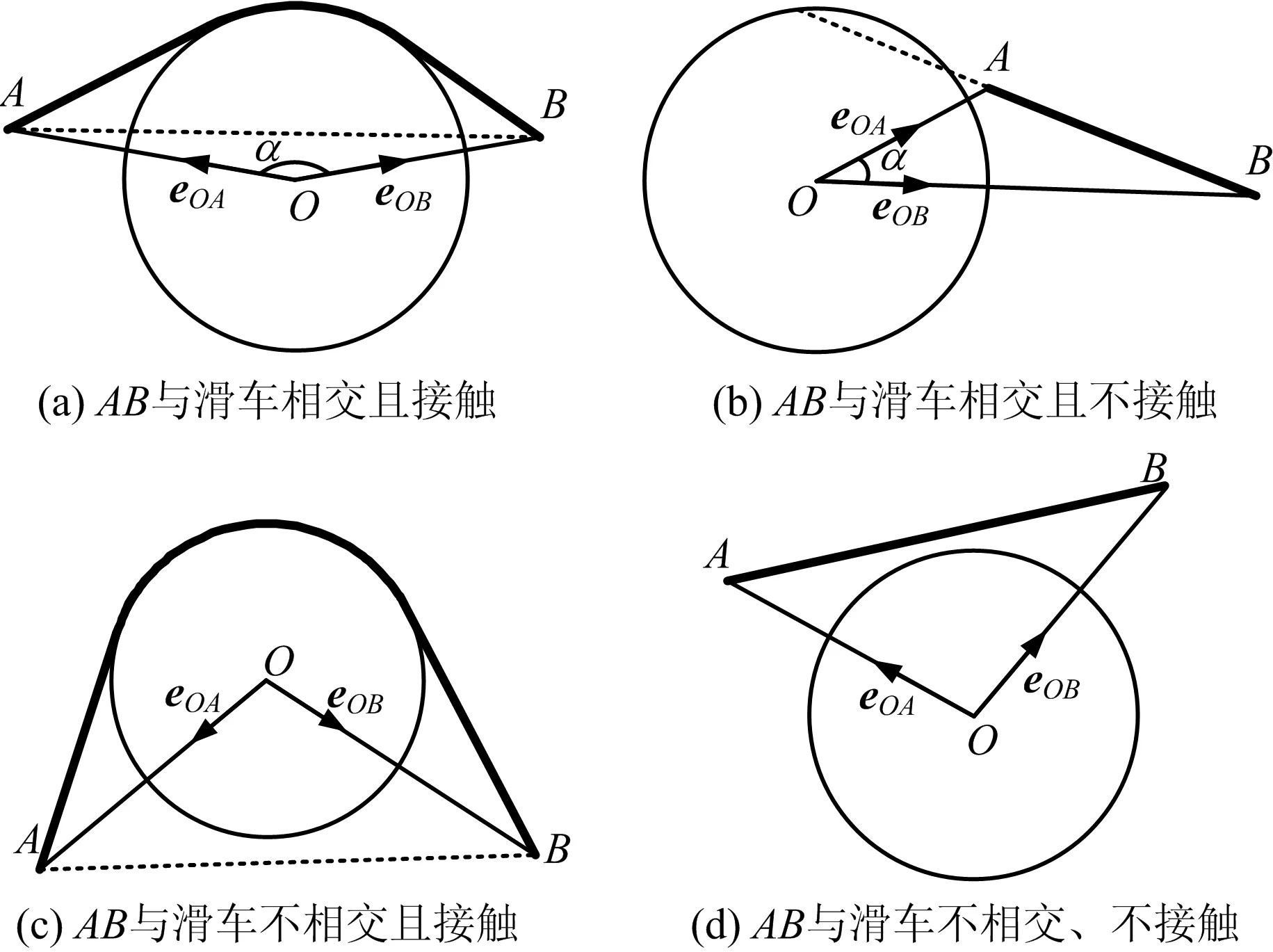
图2 导线与滑车接触情况Fig.2 Contact situation between conductor and pulley

①导线端点所在直线与滑车相交

令α=arcos(eOA·eOB)，其中eOA为从O到A点的单位矢量，eOB为从O到B点的单位矢量。则当α>90°时，导线AB与滑车接触，如图2(a)所示；当α<90°时，导线AB与滑车无接触，如图2(b)所示。

②导线端点所在直线与滑车不相交

令γk=eOA×eOB，其中k为垂直于eOA，eOB的单位矢量，方向服从右手系。当γ>0时，导线AB与滑车接触，如图2(c)所示；当γ<0时，导线AB与滑车无接触，如图2(d)所示。

当导线AB与滑车接触时，从A，B出发可分别得到与滑车相切的2条直线，为符合工程实际，以切点在上的切线为实际切线，切点分别为AO，BO，如图3所示。

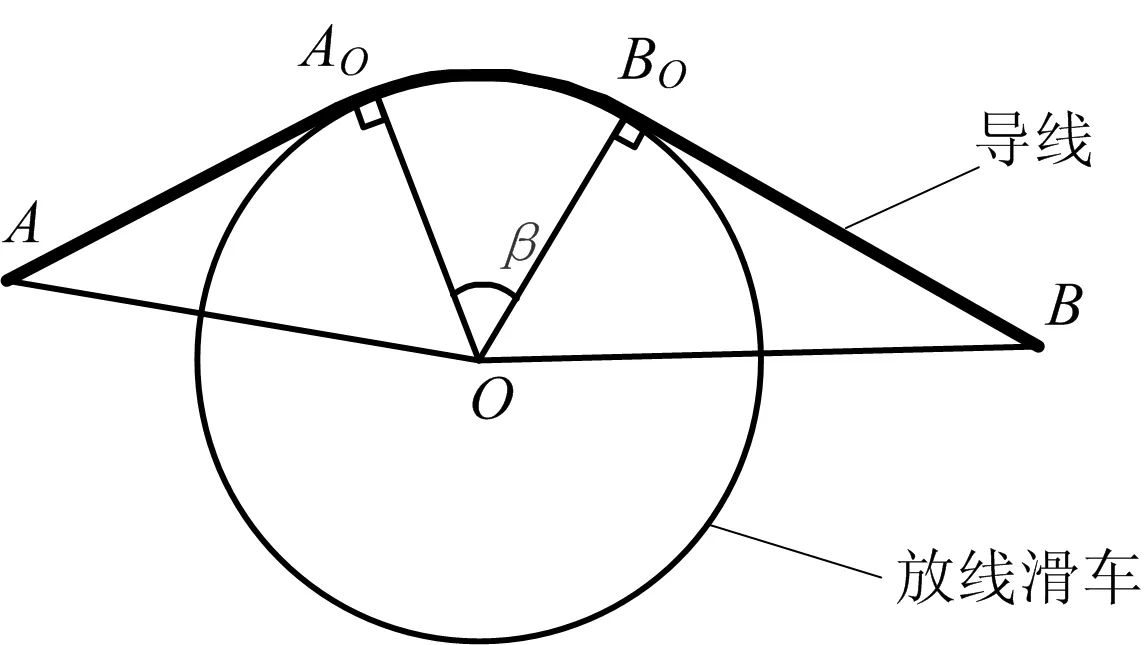
图3 导线与滑车切点Fig.3 Contact point between conductor and pulley

与滑车接触的导线AB长度如式(1)所示：

(1)

式中：sAB为导线AB长度，m；lOA，lOB分别为O到A，B的距离，m；β为导线对滑车的包络角，rad；R为滑车半径，m。

当导线与滑车无接触时，导线长度为AB间距离。

同样，当导线CD与滑车接触时，可从C，D出发得到与滑车切点CO，DO，与式(1)中相同得到与滑车接触的导线长度sCD。

2)钢套与滑车的接触

钢套在过滑车运动中，下部顶点P首先与滑车发生点接触，然后钢套的下边界PQ与滑车发生线接触，在脱离滑车时顶点Q再与滑车发生点接触，如图4所示，图中①～③表示不同的接触状态。

图4 钢套与滑车接触示意Fig.4 Schematic diagram of contact between steel sleeve and pulley

令lOP，lOQ分别为P，Q到O的距离；钢套初始长度为lBC。

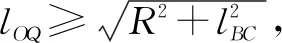
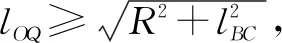
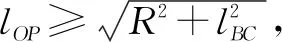
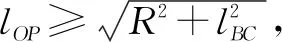
2 多体运动系统动力计算方法

2.1 有限质点法

本文采用有限质点法对导线、钢套、滑车及悬臂的运动进行分析。有限质点法采用具有集中质量的质点对结构进行空间上的离散，分析过程中采用路径单元对结构运动进行时间上的离散。

质点在单元内力和节点外力的共同作用下遵循牛顿第二定律进行运动，并以此来反映结构的动力行为[8-13]。即质点运动方程如式(2)所示：

(2)

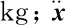
采用中心差分法来求解质点的运动方程，如式(3)所示：

(3)

式中：xn-1，xn，xn+1分别为第n-1，n，n+1个时间步的质点位置向量，m；h为时间增量步长，s；Fn为第n个时间步的质点合力矢量，N；c1，c2为考虑阻尼的计算系数[8]。

2.2 质点作用力

1)质点质量

多体系统中质点即为单元节点A，B，C，D，O。单元质量均匀集中于质点上，各质点的质量分别为mA，mB，mC，mD，mO。

2)质点合力

在第n个时间步时，已知各质点空间坐标xn，xn-1，即可获得该时间步的各质点合力。

①质点B所受合力如式(4)所示：

(4)

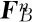
②质点C所受合力如式(5)所示：

(5)

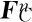
③质点D所受合力如式(6)所示：

(6)

④质点O所受合力如式(7)所示：

(7)

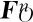
3)单元内力

①AB内力如式(8)所示：

(8)

式中：f1为导线AB单元内力，N；EAC为导线弹性模量与截面积乘积，N；lAB为导线AB的初始直线长度，m。

②CD内力如式(9)所示：

(9)

式中：f2为导线CD单元内力，N；sCD为导线CD长度，m；lCD为CD的初始直线长度，m。

③OS内力如式(10)所示：

(10)

式中：f3为悬臂OS单元内力，N；EAS为OS单元弹性模量与截面积乘积，N；sOS为质点O到S的距离，m；lOS为OS的初始直线长度，m。

单元内力f1，f2，f3可根据质点位移显式计算得到。

4)质点间作用力

下面给出质点间作用力的表达式。

①fAB如式(11)所示：

(11)

式中：eBBo，eBA分别为从B到BO、从B到A的单位矢量。

②fDC如式(12)所示：

(12)

式中：eCCo，eCD分别为从C到CO、从C到D的单位矢量。

③fCD如式(13)所示：

(13)

式中：eDDo为从D到DO的单位矢量。

④fSO如式(14)所示：

fSO=f3eOS

(14)

式中：eOS为从O到S的单位矢量。

⑤fABO如式(15)所示：

(15)

式中：eAAo为从A到AO的单位矢量。

⑥fCDO如式(16)所示：

(16)

⑦钢套质点C，B间作用力矢量如式(17)所示：

fCB=-fBC=NBCeBC

(17)

式中：NBC为BC单元内力，N；eBC为从B到C的单位矢量。

⑧fBCO如式(18)所示：

fBCO=-fOB-fOC

(18)

因钢套直径相对较小，认为滑车对P，Q点的作用力等同作用于B，C点，因此当钢套P与滑车O发生点接触时(图4中状态①)，fOB如式(19)所示：

fOB=NPeOP

(19)

式中：NP为P与滑车接触力，N；eOP为从O到P的单位矢量。

当Q与滑车O发生点接触时(图4中状态③)，fOC如式(20)所示：

fOC=NQeOQ

(20)

式中：NQ为Q与滑车接触力，N；eOQ为从O到Q的单位矢量。

当PQ与滑车发生线接触时(图4中状态②)，则：

(21)

(22)

式中：lMQ，lMP为接触点M到Q，P的距离，m；lBC为钢套初始长度，m；NPQ为接触力，N；eOM为从O到M的单位矢量。

当不发生以上接触时，对应的接触作用力值为零。

NBC，NP，NQ，NPQ不能通过显式计算得到，只能通过钢套长度约束及接触约束等隐式条件获得。

2.3 隐式约束条件

钢套为刚性体，需满足长度约束条件，如式(23)所示：

(23)

式中：xBn+1，xCn+1为第n+1个时间步B，C的位置向量，m。

当钢套顶点P，Q与滑车O发生点接触时，P，Q不能侵入滑车，则接触约束条件如式(24)～(25)所示：

(24)

(25)

式中：xPn+1，xQn+1，xOn+1为第n+1个时间步P，Q，O的位置向量，m。

当PQ与滑车发生线接触时，钢套不侵入滑车的约束条件为滑车O到PQ连线的距离等于滑车半径R，如式(26)所示：

(26)

将式(4)～(7)代入第n+1个时间步的质点位移公式(3)，再代入约束条件(23)～(26)，即可得到包括NBC，NP，NQ，NPQ等作用力的非线性方程组。可采用牛顿迭代法求解，迭代初值采用第n个时间步的结果。

2.4 系统运动过程求解

导线质点A在牵引力的作用下，向牵引侧运动，假设在通过滑车过程中维持恒定速度，则质点A的位置如式(27)所示：

(27)

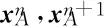
通过张力放线施工整体计算[14]，获得钢套过滑车时的张力放线速度、过滑车时导线线形及导线张力，确定vA及张力矢量TC。

在得到第n个时间步的质点位移后，即可计算质点间的方向向量，并可显式计算得到f1，f2，f3单元内力，通过隐式约束条件计算得到NBC，NP，NQ，NPQ作用力，进而根据式(3)获得第n+1个时间步的质点位移，直至运动过程结束。

3 钢套冲击滑车计算分析

在钢套通过放线滑车的过程中，运动系统的状态受到导线牵引力值、牵引角度、张力值、张力角度、滑车半径、悬臂长度、钢套厚度、钢套通过滑车速度等多种因素影响。

3.1 冲击动力过程分析

在接续管钢套的设计及放线施工过程中，主要关注钢套所受最大载荷、钢套冲击滑车时的最大导线牵引力、滑车悬挂载荷等[15]。

因此针对典型的张力放线工况，对冲击过程中滑车与钢套接触力、导线牵引力进行计算分析。

钢套在运行速度0.7 m/s、牵引角度20°、张力角度-10°、钢套厚度0.1 m、张力25 kN、悬臂长度1.0 m的工况下，钢套所受牵引力和接触力的计算结果如图5所示。

图5 钢套通过滑车过程分析Fig.5 Process analysis of steel sleeve passing through pulley

由图5可知，钢套与滑车经历了未接触—P点接触—PQ线接触—Q点接触—分离的接触力变化过程。①为钢套与滑车接触前的阶段；②为P与滑车的点接触阶段；③为PQ线接触阶段；④为Q与滑车的点接触阶段；⑤为钢套与滑车的分离阶段。整个过程中钢套与滑车的接触力最大值发生在阶段③。

通过大量计算发现悬臂长度lOS对接触状态有较大影响，因此，其他参数相同的情况下进行悬臂长度2.0 m情况下钢套过滑车过程分析。钢套牵引力和接触力如图6所示。

图6 悬臂长度2.0 m时钢套通过滑车过程分析Fig.6 Analysis on process of steel sleeve passing through pulley with cantilever length of 2.0 m

由图5与图6对比可知，当悬臂长度增加，滑车的摆动周期加长，钢套通过放线滑车的运行状态发生复杂变化，产生“线-点-线”接触的反复变化过程。图6中，①为钢套与滑车接触前的阶段；②为P与滑车的点接触阶段；③为第1次PQ线接触阶段；④为Q与滑车的第1次点接触阶段；⑤为第2次PQ线接触阶段；⑥为Q与滑车的第2次点接触阶段；⑦为第3次PQ线接触阶段；⑧为Q与滑车的第3次点接触阶段；⑨为钢套与滑车的分离阶段。

3.2 重要因素的影响分析

针对实际特高压输电线路工程，对运行速度、牵引角度、张力角度、钢套厚度、张力值、悬臂长度6个因素进行重点分析，计算工况及参数取值见表1。

表1 钢套通过放线滑车计算工况及参数Table 1 Calculation conditions and parameters of steel sleeve passing through stringing pulley

各工况下最大导线牵引力、最大P点接触力、最大PQ线接触力、最大Q点接触力的变化曲线如图7～12所示。

图7 随速度变化曲线Fig.7 Change curves with velocity

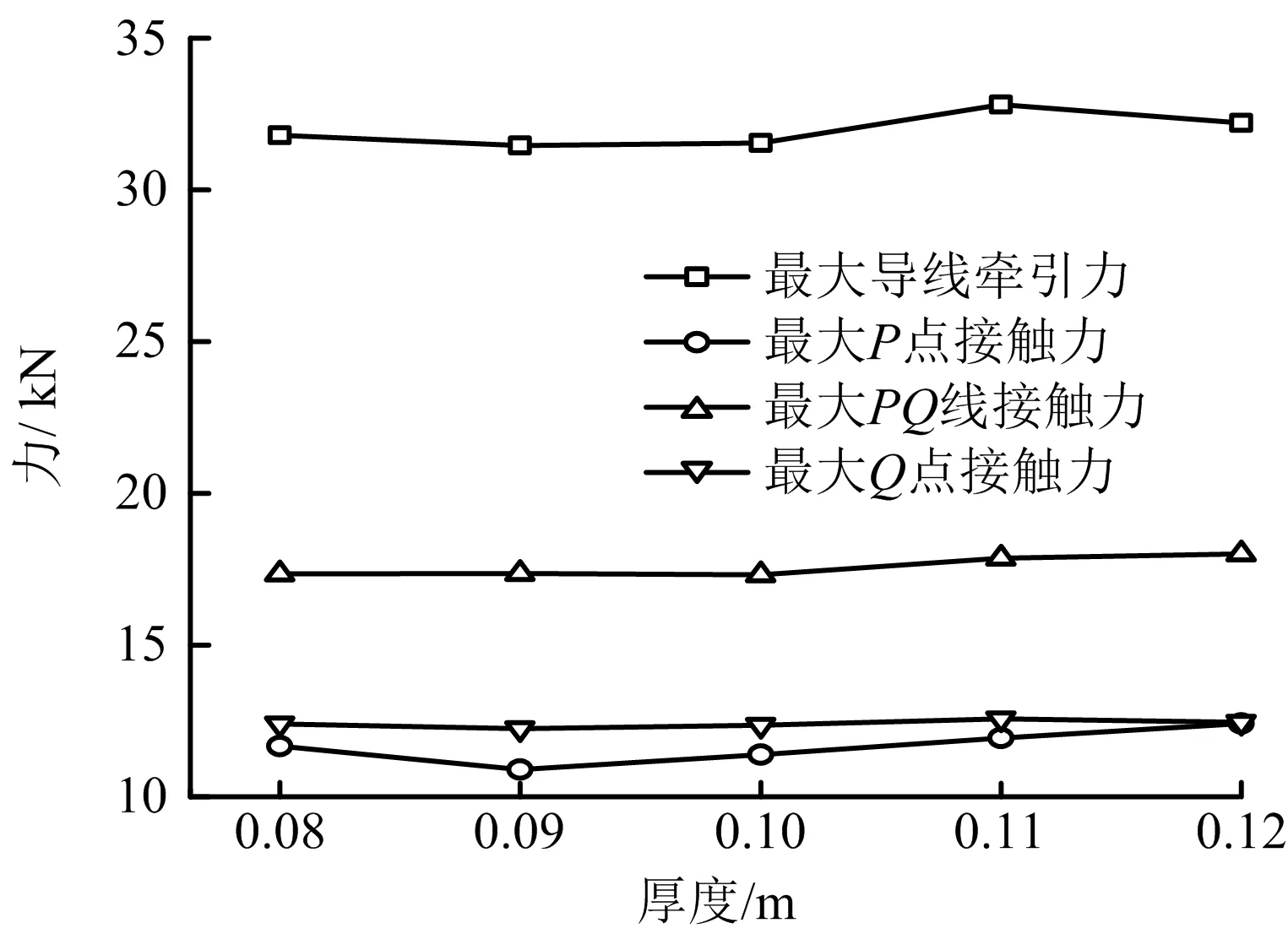
图8 随厚度变化曲线Fig.8 Change curves with thickness

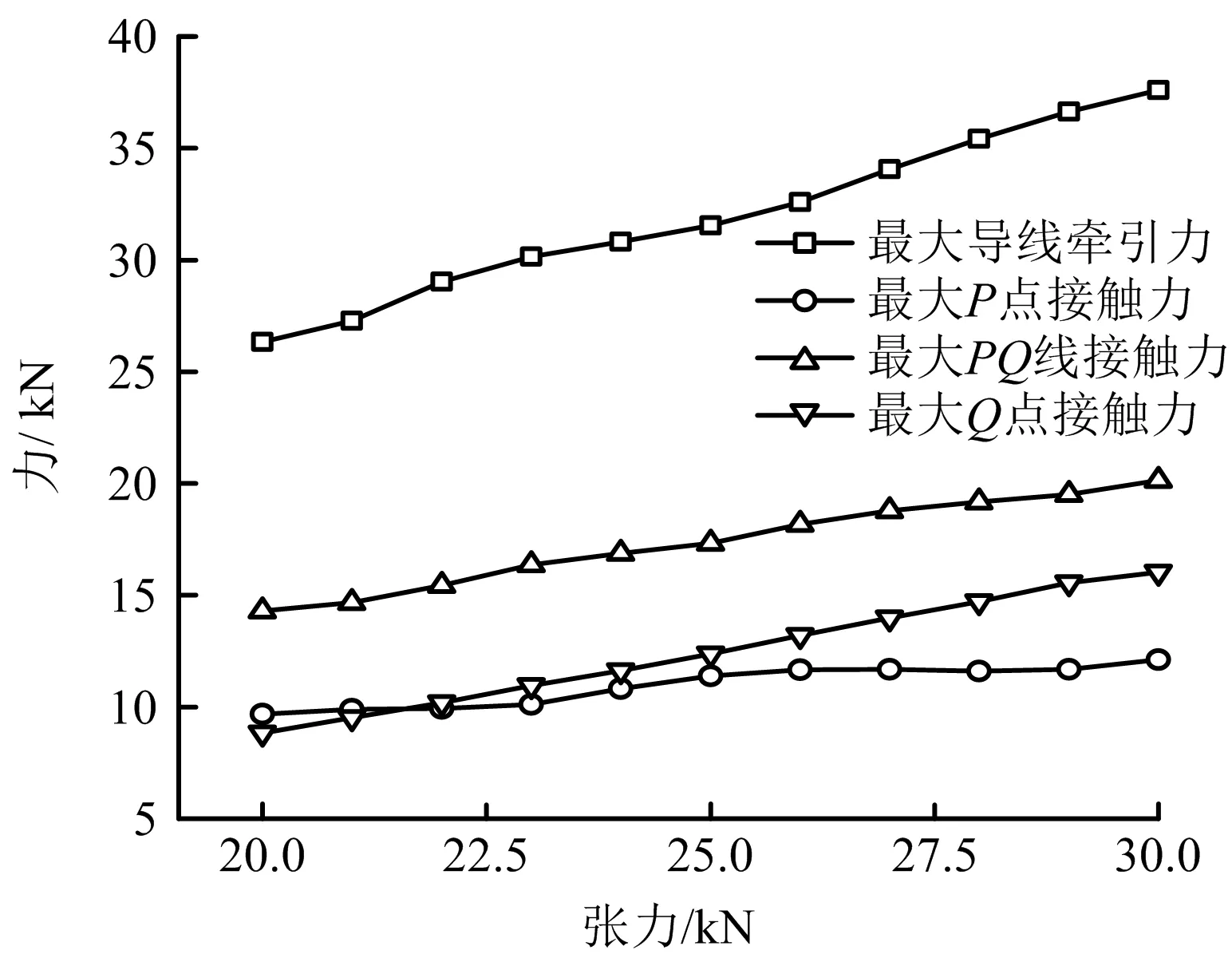
图9 随张力变化曲线Fig.9 Change curves with tension

图10 随悬臂长度变化曲线Fig.10 Change curves with cantilever length

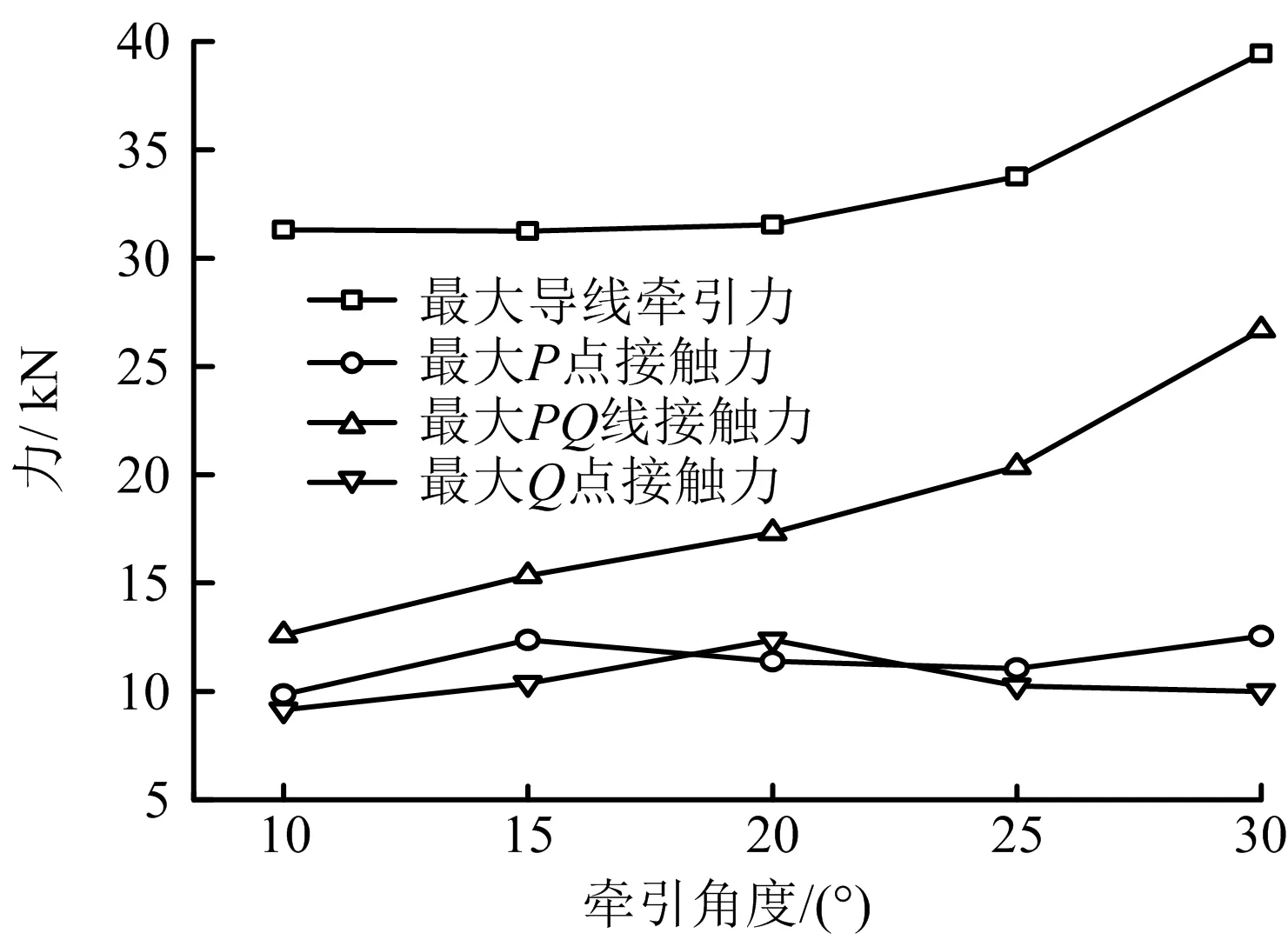
图11 随牵引角度变化曲线Fig.11 Change curves with traction angle

图12 随张力角度变化曲线Fig.12 Change curves with tension angle

由图7～12可知，钢套通过放线滑车过程中：1)张力对牵引力、点接触力、线接触力均有较大影响，且各结果的变化趋势与张力一致；2)牵引速度、钢套厚度、悬臂长度对牵引力、接触力的影响较小；3)随着牵引角度、张力角度绝对值的增加，钢套对滑车作用合力相应增加，造成过滑车过程中最大线接触力的增长；而且θ，φ的增长影响钢套通过滑车的连续性，造成最大牵引力的大幅增长，但过滑车过程中前端点P和末端点Q的接触力基本未受影响；4)钢套线接触力大于钢套前端点和末端点接触力。

4 结论

1)本文建立输电线路张力放线施工中导线接续管钢套通过放线滑车的多体运动系统，提出运动系统中各结构体的接触判别方法、接触力的隐式计算方法，形成接续管钢套通过滑车的动力过程计算方法，可实现大高差、大转角等地形条件下的滑车通过性精细分析。

2)针对输电线路施工中的典型工况，进行钢套过滑车冲击过程分析，总结运动过程中接触状态、导线牵引力的变化规律。并针对接续管钢套设计及工程施工中关注的重要因素，设计包括各类因素变化的计算工况，完成不同工况下钢套过滑车过程的计算，分析导线张力、钢套厚度、牵引角度等因素对钢套与滑车接触力的影响。

3)方法为输电线路工程施工提供技术支持，针对多工况的分析结果可为导线接续管、放线滑车的设计提供参考依据。