考虑旅客携行行为的安检系统服务参数优化研究*
晋良海,雷文凡,闵 露,郑霞忠,陈 述,江 新,2
(1.三峡大学 水利与环境学院,湖北 宜昌 443002; 2.三峡大学 安全生产标准化评审中心,湖北 宜昌 443002;3.三峡大学(湖北)安环科技有限公司,湖北 宜昌 443002; 4.广西国土资源规划院 自然资源调查勘测分院,广西 南宁 530022)
0 引言
公共交通安检系统的旅客流量大、行为样态复杂,使得旅客人体安检与行李安检之间往往存在速度差。由于速度差的存在,使得旅客等待时间变长,局部区域易产生滞留等待现象,导致安检服务效率下降甚至产生群体性拥挤、踩踏等安全事故。因此,基于旅客携行行为视角,研究旅客人体安检与行李安检之间存在的速度差问题,并优化安检系统服务设施配置及参数,有利于提高公共交通安检系统服务效率。
从国内外安检系统优化理论的研究成果来看,主要研究方法可以大致分为以下2类:1)对旅客移动特点进行分析,建立旅客移动模型,包括社会力模型、元胞自动机模型等,仿真现实场景,优化安检设施布局。2)综合考虑旅客属性特征与安检流程,应用Logit模型、排队网络、多元线性回归等研究方法,找出影响安检服务效率的关键因素,制定高效的安检疏导策略。
对旅客移动特点的研究方面,Zheng等[1]以动态参数的元胞自动机模型模拟地铁旅客的等待和上下车行为;窦敏[2]建立客流组织离散模型,分析安检通道客流拥堵分布、等待时间、排队队长等多指标,并提出优化方案;宫宇姝[3]建立进站流线动态仿真模型,模拟旅客在高架层进站区的进站过程;孙启鹏等[4]构建和仿真城际旅客出行服务流程Petri网模型,定量分析旅客服务流程中需要改进的重点环节;张天炫等[5]利用优化社会力模型构建机场旅客安检排队仿真模型,结果表明优化模型明显优于传统模型;彭凯贝等[6]设定重点和常规安检通道,运用AnyLogic软件仿真安检流程,找出最优化的风险阈值和安全通道配置数。
综合考虑旅客属性特征与安检流程研究方面,Skorupski等[7]采用模糊推理系统对随身行李进行评价,并提出行李筛选;基于串联和并联混合的排队网络,刘洁等[8]验证交换安检设备和自动检票闸机物理顺序能有效减少排队等待时间;陈鹏等[9]对旅客特征数据进行统计分析,发现安检过程中的等待时间与疏散时间主要取决于旅客的队列长度;赵元棣等[10]建立2种安检排队模型,对比分析发现安检通道最低配置数量随着旅客到达率增加而增加;基于排队论,姚加林等[11]建立车站安检设备开放数量与实时客流需求相匹配的优化模型;郑勋等[12]利用多元线性回归方法建立安检机服务时间模型;基于排队网络结构模型,Li等[13]发现分离身份证、行李和旅客检查的开放网络结构能显著改善安检系统性能;为优化机场安检流程,胡艳敏等[14]提出基于Petri网和排队论的优化模型,发现等待时间趋于平均化,从而提高效率。
以上研究成果对优化安检服务设施配置、提高安检系统服务效率具有一定的借鉴意义,但未考虑旅客流与行李流的速度差问题,而二者的速度差对安检系统服务效率影响较为显著。为此,本文考虑旅客携行行为,分析安检系统服务流程,构建安检系统的Jackson排队网络模型;研究旅客人体安检和行李安检之间存在的速度差,分析携行行为条件下不同情境中旅客提取行李前的等待时间,修正安检系统排队网络模型;优化安检系统服务参数,实现系统服务设施的最优配置,为公共交通安检系统设计与管理提供依据。
1 安检系统排队网络模型
1.1 安检流程的网络化描述
在地铁、高铁等大型公共客运站,旅客到达安检系统后,接受安全检查的环节主要包括安放行李、旅客安检、行李安检、提取行李和行李的2次检查。旅客在提取行李时主要有“等待取行李”和“绕行取行李”2种携行行为。“等待取行李”行为是指携带行李的旅客从安检门出来后,走到滑台口处等待提取行李的行为,而“绕行取行李”行为是指携带行李的旅客从安检门出来后,沿着安检机走到围栏的对面一侧提取行李的行为。将发生“等待取行李”行为的旅客提取行李区域设置为“提取行李”驻点1,将发生“绕行取行李”行为的旅客提取行李区域设置为驻点2,如图1所示。
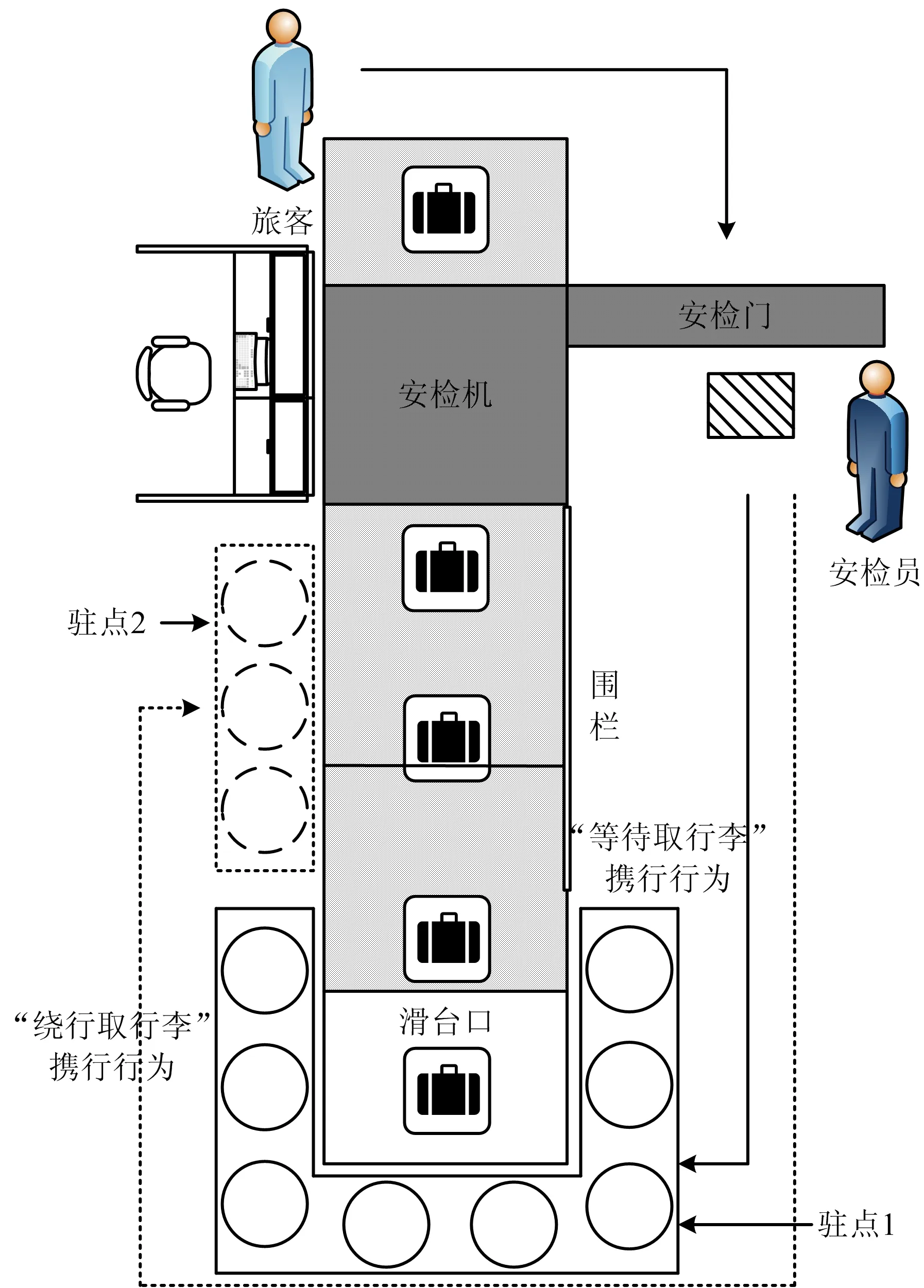
图1 提取行李的2种携行行为样态Fig.1 Two styles of carrying behavior for baggage claim
以安全检查的环节为服务节点i(i=1,2,3,…,6),以旅客流和行李流为箭线,构成公共交通安检系统的运行流程,如图2所示。由图2可知,各服务节点的连接和旅客及行李的流向构成安检系统排队网络。旅客在接受1个节点服务后,以一定概率转移至另一节点或者离开系统,在假定无限顾客源、外部旅客到达及被服务满足排队论规律的情况下,该网络可近似看作Jackson排队网络。
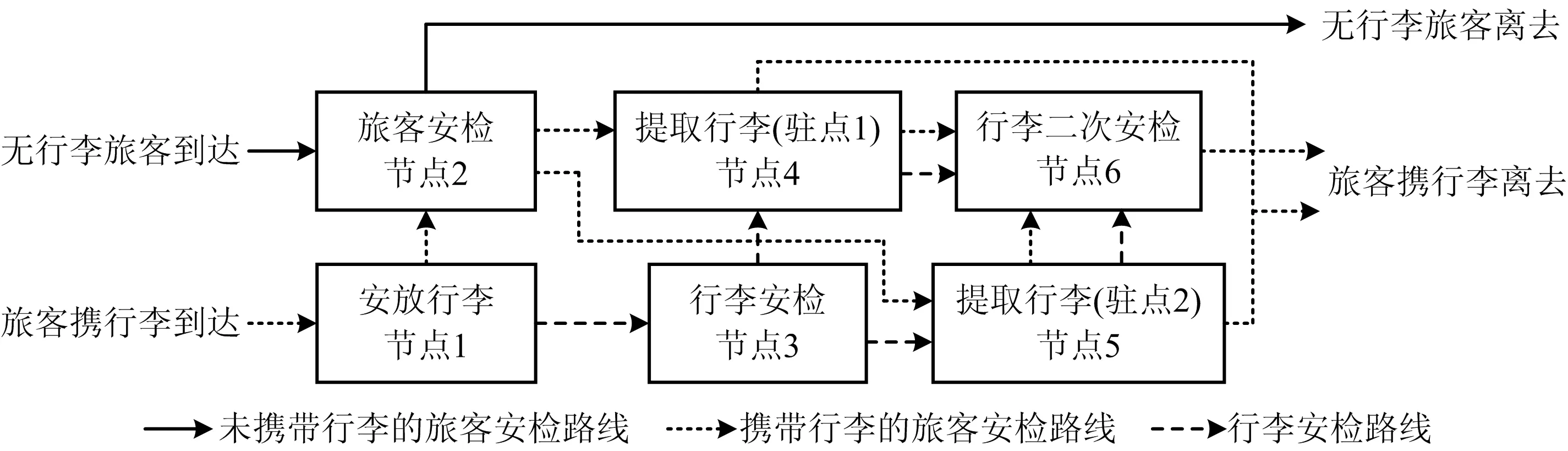
图2 公共交通的安检系统运行流程Fig.2 Operation process of security inspection system for public transportation
1.2 Jackson排队网络模型
1)模型假设
假设1:未携带行李的旅客与携带行李的旅客从外部进入安检系统的到达过程均满足泊松分布。
假设2:排队规则为先到先服务的等待制。
假设3:各服务节点(“行李检查”服务节点除外)对旅客的服务时间满足相互独立的负指数分布,满足M/M/s的多服务台排队模型;“行李检查”服务节点的服务时间属于定长分布。
假设4:旅客原地整理行李的行为持续时间属于旅客提取行李的服务时间;旅客的逗留行为不占用节点的服务位置。
2)模型建立
设λ1,λ2分别为携带行李旅客的外部平均到达率、未携带行李旅客的外部平均到达率,rij(i,j=1,2,4,5,6)为旅客从节点i转移到节点j的概率,σj(i=1,2,4,5,6)为节点j的旅客总到达率,aj为节点j的外部平均到达率,其计算如式(1)所示:
(1)
设旅客从节点2转移到节点4的概率为Pc,即r24=Pc,设旅客从节点4或者5转移到节点6的概率为Pr,即r46=r56=Pr。依据安检系统运行流程(图2),构建排队网络各节点旅客或行李转移概率图,如图3所示。
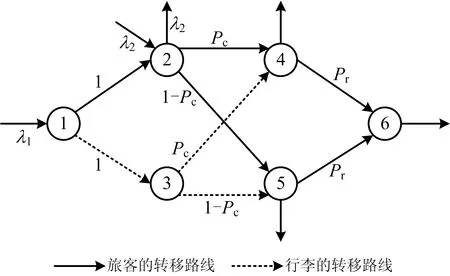
图3 节点转移概率Fig.3 Node transition probability map
各节点的旅客总到达率如式(2)所示:
(2)
旅客主动选择在驻点1或者驻点2提取行李,根据驻点位置的不同,行李安检固定时长服务时间发生相应的改变。设当旅客选择驻点1,2时,“行李检查”的服务时间分别为D1,D2,s;设旅客从安检门走到提取行李驻点1,2的中心位置距离分别为Ls1,Ls2,m。经测量,传送带末端能保证2名旅客同时提取行李,则表达式如式(3)~(6)所示:
(3)
(4)
Ls1=l1+s5w+((s4-2)w/2+w)/2
(5)
Ls2=l1+3s5w/2+(s4-2)w+w
(6)
式中:l0为安放行李点到安检机出口边缘的距离,m;l1为安检门出口边缘到安检机出口边缘的距离,m;w为服务台的宽度,也是旅客的平均肩宽,m,一般取0.4 m;si为节点i的服务台数量,台;Vm为安检机传送带的移动速度,m/s。
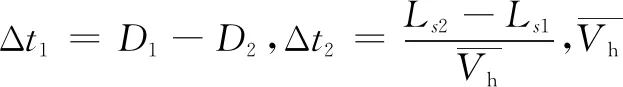
(7)
式中:α,β为比例系数,α+β=1;W2为旅客安检服务的逗留时间,s;μi为服务率;μ4,μ5分别是节点4,5的平均服务率。
旅客行李被检测异常的概率为p0,且被检测异常的行李均需要经过节点6的服务,因此符合式(8):
Pr=p0
(8)
1.3 模型修正
考虑旅客人体安检和行李安检之间存在的速度差现象,厘定携行行为条件下4种不同情境的行李提取行为样态,计算旅客提取行李前的等待时间如图4所示。
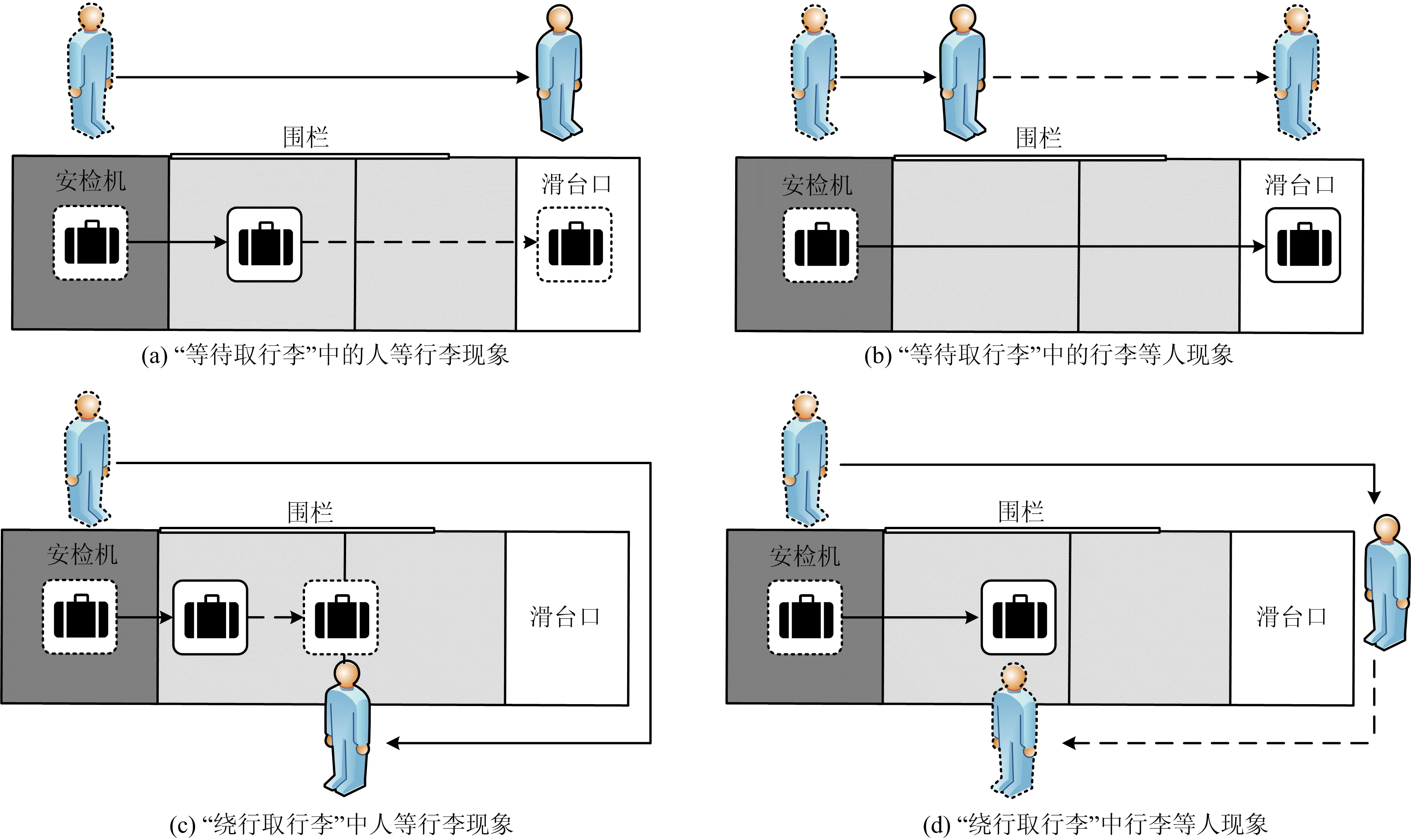
图4 行李提取行为样态Fig.4 Behavior styles of baggage claim
根据图4描述的4种情境计算旅客提取行李前的等待时间。
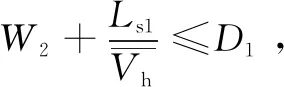
T1=D1-W2
(9)
式中:T1为“等待取行李”中的人等行李现象发生时,旅客提取行李前的等待时间,s。
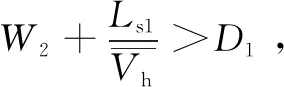
(10)
式中:T2为“等待取行李”中的行李等人现象发生时,旅客提取行李前的等待时间,s。
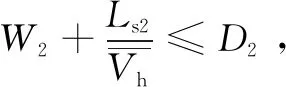
T3=D2-W2
(11)
式中:T3为“绕行取行李”中人等行李现象发生时,旅客提取行李前的等待时间,s。
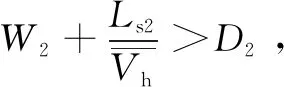
(12)
式中:T4为“绕行取行李”中行李等人现象发生时,旅客提取行李前的等待时间,s。
综合以上4种情况,旅客提取行李前的平均等待时间Tw计算如式(13)所示:
Tw=Pc[(1-P1)T1+P1T2]+(1-Pc)[(1-P2)T3+P2T4]
(13)

2 安检系统服务参数优化
以安检系统稳态条件下单位时间的平均总费用为因变量,各服务节点服务台数量为自变量,构建安检系统服务水平最优目标函数,求解服务水平最优条件下安检系统各服务节点服务台最优数量配置。在考虑1台安检机、安检机传送带速度不变的情况下,目标函数如式(14)~(15)所示:
(14)
(15)
式中:C为稳态条件下安检系统单位时间的平均总费用,元;si为节点i的服务台数量,台;Lqi为节点i等待的顾客平均数;ρi为节点i的平均服务强度;Csi(i=1,2,4,5,6)为节点i每个服务台单位时间的服务成本,包括单位时间安全员的工资、安检门和金属探测仪的折旧费、修理费用等,元;Cw为每位旅客单位时间的等待成本,元;Cs3为安检机单位时间的折旧费、修理费用以及安检机操作员的工资,元;subi为节点i的服务台配置数量的上限值,台。
根据服务节点是否参与旅客提取行李前平均等待时间的计算,可以将目标函数(14)拆分成式(16)~(18)(Cs3为常数,不作考虑),分别求目标函数最小值,最后由C=C1+C2+C3+Cs3得到系统最小成本值。由目标函数(14)拆分出的目标函数如式(16)~(18)所示:
minC1=Cs1s1+CwLq1
(16)
minC2=Cs6s6+CwLq6
(17)
(18)
安检系统的优化问题可以看作是多服务节点的M/M/s模型最优服务台数求解问题。本文中C1和C2的求解可采用一般的边际分析法,而C3中s2,s4,s5的求解不相互独立,采用如图5所示的算法框图来求解最小成本的C3。
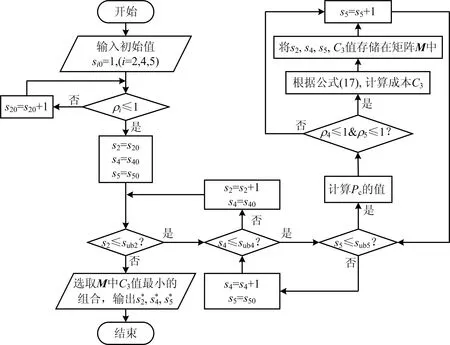
图5 最小成本C3求解程序框Fig.5 Block diagram for solving program box of minimum cost
3 案例分析
3.1 输入参数的赋值
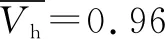
在人流高峰且连续的时段,对携带行李旅客和未携带行李旅客的到达情况进行统计,共选取3个时间段,统计人数分别为122,146,136,得到外部平均到达率λ1=0.641,λ2=0.040。在人流高峰时端段,随机观察各服务节点安检人员对旅客的服务时间,计算各服务节点平均到达率σi和服务率μi。通过市场调查安检员工作的薪资情况以及安检设备的折旧与维修费用,计算各服务节点服务台的服务成本,计算结果见表1。参考文献[15],以s为单位时间,确定旅客的等待成本Cw=0.027元。
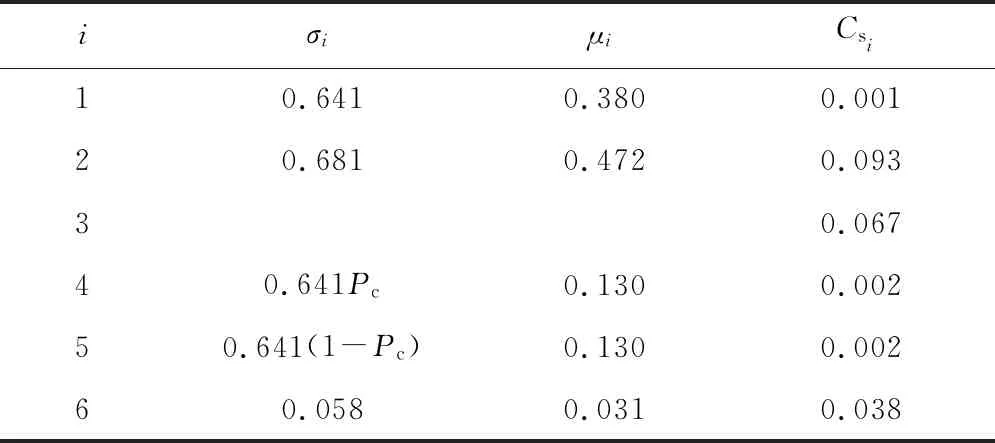
表1 各服务节点的输入参数Table 1 Input parameters of each service node
3.2 服务参数优化
在确定各服务节点的输入参数后,通过边际分析法可以求出节点1,6的服务台最优配置数量分别为4和3,设节点的服务台配置数量的上限值subi=10(i=2,4,5),利用程序求解出729组满足ρi≤1的s2,s4,s5,C3,通过比较C3值,找出C3值最小情况下节点2,4和5的服务台最优配置数量分别为2,3和8。目标函数最小值C1=0.004 5,C2=0.120 7,C3=0.412 3,系统最小成本值为0.604 5元/s。
3.3 优化结果分析
1)优化前后排队指标对比
优化前后各节点排队输出指标见表2。由表2中数据可知,经过优化后,“旅客安检”节点和“提取行李驻点2”节点的服务强度均小于1,“提取行李驻点2”节点的等待队长和等待时间几乎可以忽略不计,“旅客安检”节点的服务强度相对较高的原因是增设单位服务台的成本较高。“安放行李”节点优化前的服务强度较高,但在增设服务台后,服务强度从0.843降至0.421,旅客等待时间从5.167 s降至0.030 s,服务性能得到极大的提升,在优化后,当旅客到达安检系统时,几乎不需要排队等待,就可以开始安检。“提取行李驻点1”节点在优化前的各项指标均较好,但从安检系统总体利益出发,在优化后减少服务台数量,虽然等待时间从1.286×10-5s增至0.526 s,但还在旅客的接受范围内。“行李二次安检”节点的优化前后服务台数量一致,因此各项排队输出指标相同,表明实际配置不仅满足旅客的服务需求,而且达到系统最优化。
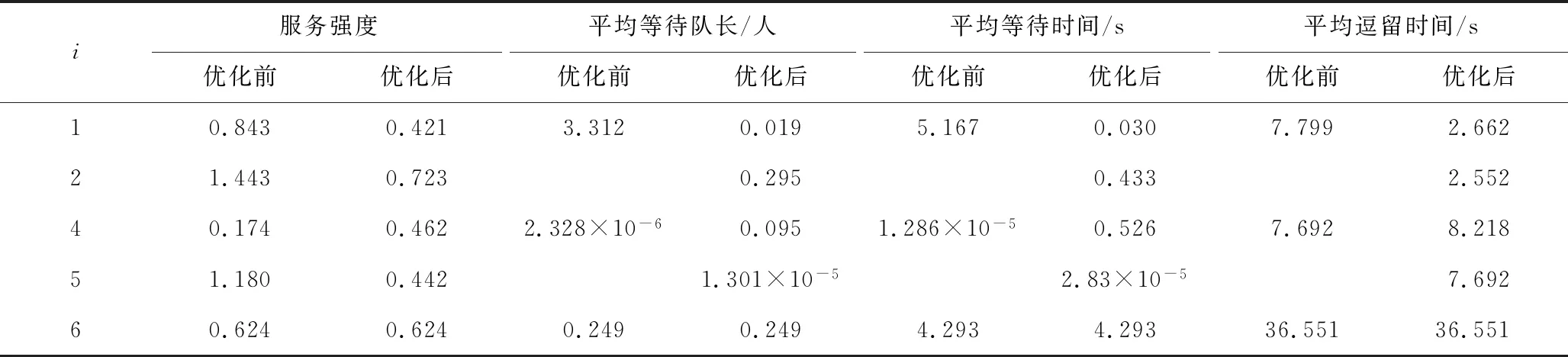
表2 优化前后各节点排队输出指标Table 2 Queued output indexes of each node before and after optimization
2)优化后2种提取行李行为的效率分析
当“旅客安检”节点服务台数量s2=2时,“提取行李驻点1”节点服务台数量s4和“提取行李驻点2”节点服务台数量s5与旅客提取行李前的等待时间Tw的关系如图6所示。
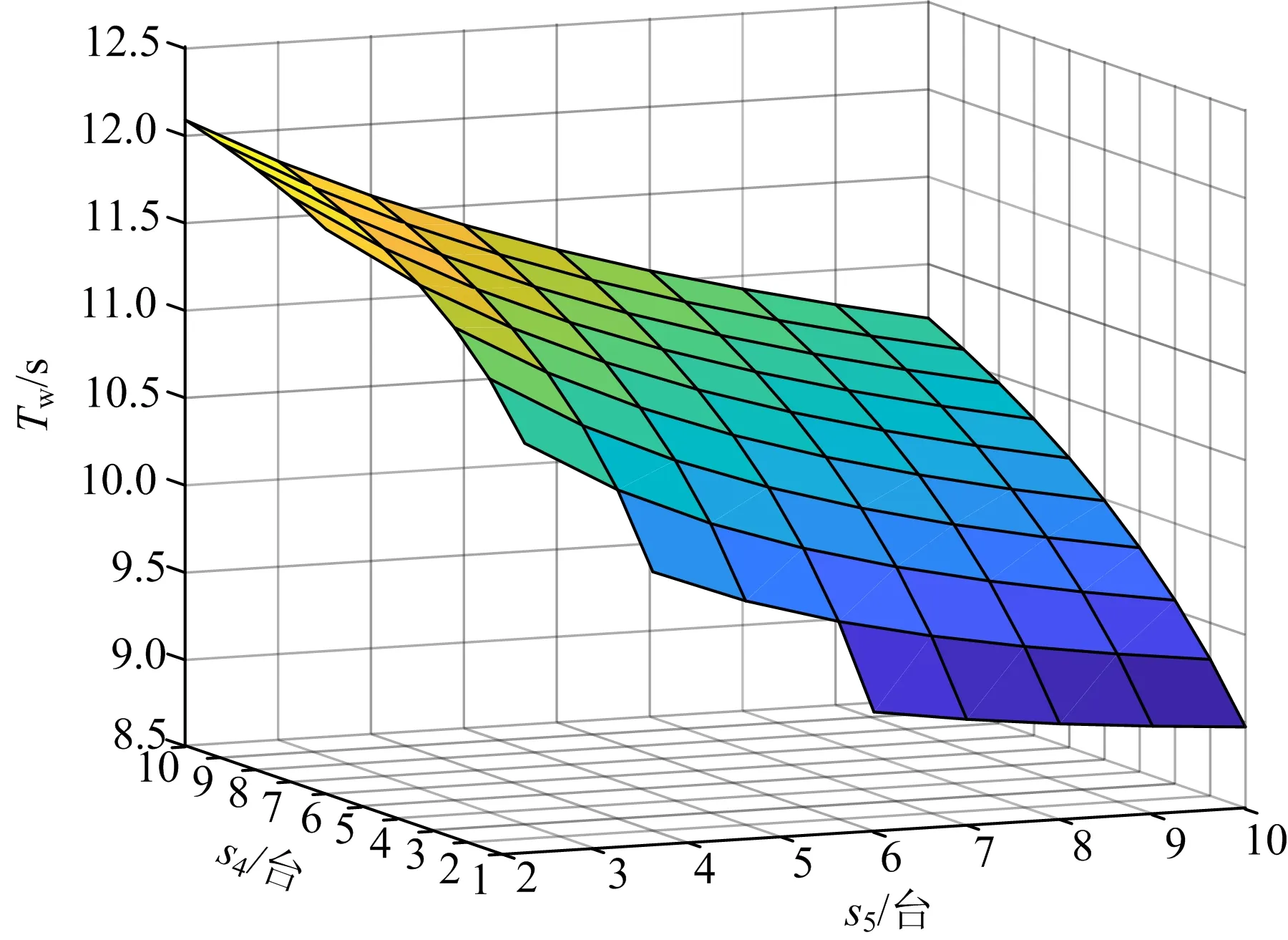
图6 “提取行李驻点1”和“提取行李驻点2”节点服务台数量与旅客平均等待时间的关系Fig.6 Relationship between quantity of node service counter and average waiting time of passengers at baggage claim station 1 and 2
由图6可知,当s5≤6时,s5取值越小,ρ4或ρ5大于1出现的可能性越大,而服务强度大于1表明“提取行李驻点1”或者“提取行李驻点2”节点的等待队列长度可能会无限增长,因此s5取值应适当增大。Tw能取得最大值为12.09 s,此时s4=10,s5=2;Tw能取得最小值为8.97 s,此时s4=1,s5=10。当安检系统经过优化后,增加采取“绕行取行李”行为的旅客比例,系统中旅客提取行李前的平均等待时间会显著降低,而增加“等待取行李”行为的旅客比例,系统中旅客提取行李前的平均等待时间会显著提高。因此,采取合理的措施(例如设置引导通道),可使采取“绕行取行李”行为旅客数量比例适当增加,有助于缓解客流高峰时期安检系统的压力。
4 结论
1)考虑4种不同情境下旅客提取行李前的等待时间,修正安检系统排队网络模型,使得安检服务设施配置数量在安检服务成本与旅客等待成本之间取得最优值,显著提升安检系统服务性能。
2)优化模型不仅能改善安检服务设施配置效果,而且能显著降低系统稳态条件下的等待队长;增加采取“绕行取行”行为旅客比例,能显著降低旅客提取行李前的平均等待时间。
3)鉴于本文模型仅考虑旅客的2种提取行李行为,旅客携行行为样态特征及发生函数需进一步研究。
——国外课堂互动等待时间研究的现状与启示

