基于模糊规则和BFS算法的行人疏散模型研究*
翟龙真,冯绍红,文 哲,王 迪
(1.南京航空航天大学 经济与管理学院,江苏 南京 211100;2.东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引言
随着国家现代化、城市化水平的显著提高,各类大型活动中心以及交通枢纽等场所的高密度聚集活动愈加频繁。而突发事件导致的严重危害使人群安全问题日益突出。因此,研究疏散机理,构建符合真实情况的行人疏散模型,准确再现并预测行人的疏散行为,并采取干预措施,对维护社会公共安全具有重要意义。
人群疏散模型主要从宏观和微观2个方面展开。微观模型从时间与空间维度上划分,包括连续型模型和离散型模型。1995年,Helbing等提出社会力模型(Social-Force,SF),后来的连续性模型均在此基础上改进[1];离散型模型最具代表性的是元胞自动机(Cellular Automaton,CA)模型,由于其成熟的理论体系、简单的演化规则,元胞自动机模型被广泛应用于行人疏散领域[2-4]。考虑到行人感知信息的模糊性,文献[5-6]利用模糊推理方法建立多出口房间环境下行人出口选择行为模型,建立模糊元胞自动机模型(fuzzy cellular automata,FCA),优化行人出口选择机制,以更加真实地描述疏散过程。虽然FCA在疏散决策方面已有大量研究,但较少对行人移动速度进行研究。以往行人移动速度多是利用函数方程的方法精确计算,事实上行人移动速度的确定需要根据行人对周围环境的感知进行调整,信息的模糊性与动态性导致移动速度具有同样的特征。同时,从以往的速度公式中可以看出,速度仅由环境中的人群密度决定,未考虑其他因素的影响,其真实性有待商榷。在疏散方向及疏散路线方面,Schadschneider等[7]修正基于元胞自动机的领域模型,通过静态领域和动态领域建立行人的移动选择偏好矩阵,实时调整行人的移动概率,实现行人移动过程中的相互作用;杨立中等[8]、Zhu等[9]从人员行为的角度出发,提出基于元胞自动机的人员行为微观离散模型。以上研究重点分析行人与出口的距离、元胞被占领状态和出口附近的行人密度等因素对移动方向的影响,未考虑真实情况下行人移动速度的变化以及对出口选择行为的影响。因此本文在以上研究的基础上,将模糊推理理论引入元胞自动机模型,结合人群密度和行人相对距离对移动速度的影响,建立动态模糊速度模型;融合危险度和动态参数模型的思想,建立基于双端队列的广度优先搜索(Breadth First Search,BFS)算法,使元胞向危险度更低的方向移动,使模型更加符合真实情况。同时提出基于排队理论的出口疏散机制。利用所建模型对行人疏散过程中的疏散时间、疏散速度等现象进行讨论,为应急预案与应急管理提供依据,从而提升应急管理的能力与水平,保障社会公共安全。
1 模型建立
1.1 模型假设
1)元胞自动机扩展的Moore型结构
在离散二维空间内建立元胞自动机模型,每个元胞只能容纳1个行人,每个行人只能占据1个元胞,且位于元胞中心。行人与被占据的元胞是一一对应的关系。每个元胞的边长为0.4 m。
本文采用扩展的Moore型邻居。行人可以向周围8个方向(编号1~8)移动,或停在原始位置,如图1所示。把行人在1个时间步长内可以移动的位置定义为行人的移动领域。

图1 元胞自动机扩展的Moore型邻居Fig.1 Extended Moore type neighbor in CA
2)期望移动速度
行人初始行走速度为0.9~1.5 m/s,正常状态下的速度为1.25 m/s,应急疏散情况下期望速度为2.5 m/s[10]。
3)信息感知
行人从环境中感知到的信息包括行人与最近障碍物的距离和感知区域内人群的密度。本文感知区域为邻居半径r=5的邻居空间,在各移动方向上为5×5的矩阵(如图1所示)。障碍物定义为感知范围内任何妨碍行人移动速度的对象,如其他行人、墙壁等。人群密度是单位面积上的人员数量,人/m2。
1.2 基于模糊规则与BFS算法的行人疏散模型
1)动态模糊速度模型的建立
影响人员疏散速度的主要因素包括移动方向上人员与障碍物的距离和人群密度[11-13]。而人员从环境中获取的距离信息和密度信息均是主观感知信息,具有不确定性和不精确性,因此运用模糊推理理论建立动态模糊速度模型。模糊推理系统主要包括模糊化、模糊规则库、模糊推理方法和去模糊化4部分。本文建立以行人与最近障碍物的距离D和感知范围内的障碍物密度E为输入,以速度V为输出的mamdani型动态模糊速度模型。
模糊变量的定义域以及覆盖定义域的模糊集合数量根据专家经验知识和实验数据决定。输入变量行人与最近障碍物的距离D,其定义域取值范围为0~2.83 m,由3个模糊集{Very-Near(VN),Near(N),Far(F)}表示,分别代表“非常近”“近”和“远”,采用欧式距离方法计算[12]。利用F统计方法确定模糊集合“VN”“N”和“F”的隶属度,并采用回归方法选择拟合度最高的梯形隶属函数为模糊变量的隶属函数,距离隶属函数如图2所示。输入变量障碍物密度E的定义域取值范围为0~5人/m2,由3个模糊集{Low(L),Medium(M),High(H)}表示,分别表示“低”“中”和“高”。移动领域内目标方向上的人群密度采用梯形隶属函数,障碍物密度隶属函数如图3所示[10]。输出变量行人移动速度V的定义域为0~5 m/s,移动速度由3个模糊集{Slow(S),Medium(M),Fast(F)}表示,速度隶属函数为梯形[12],如图4所示。
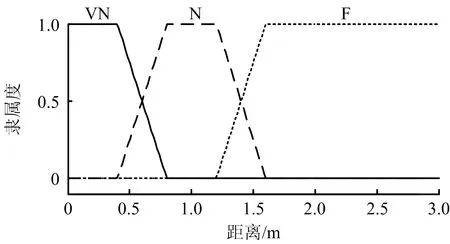
图2 距离隶属函数Fig.2 Membership function of distance
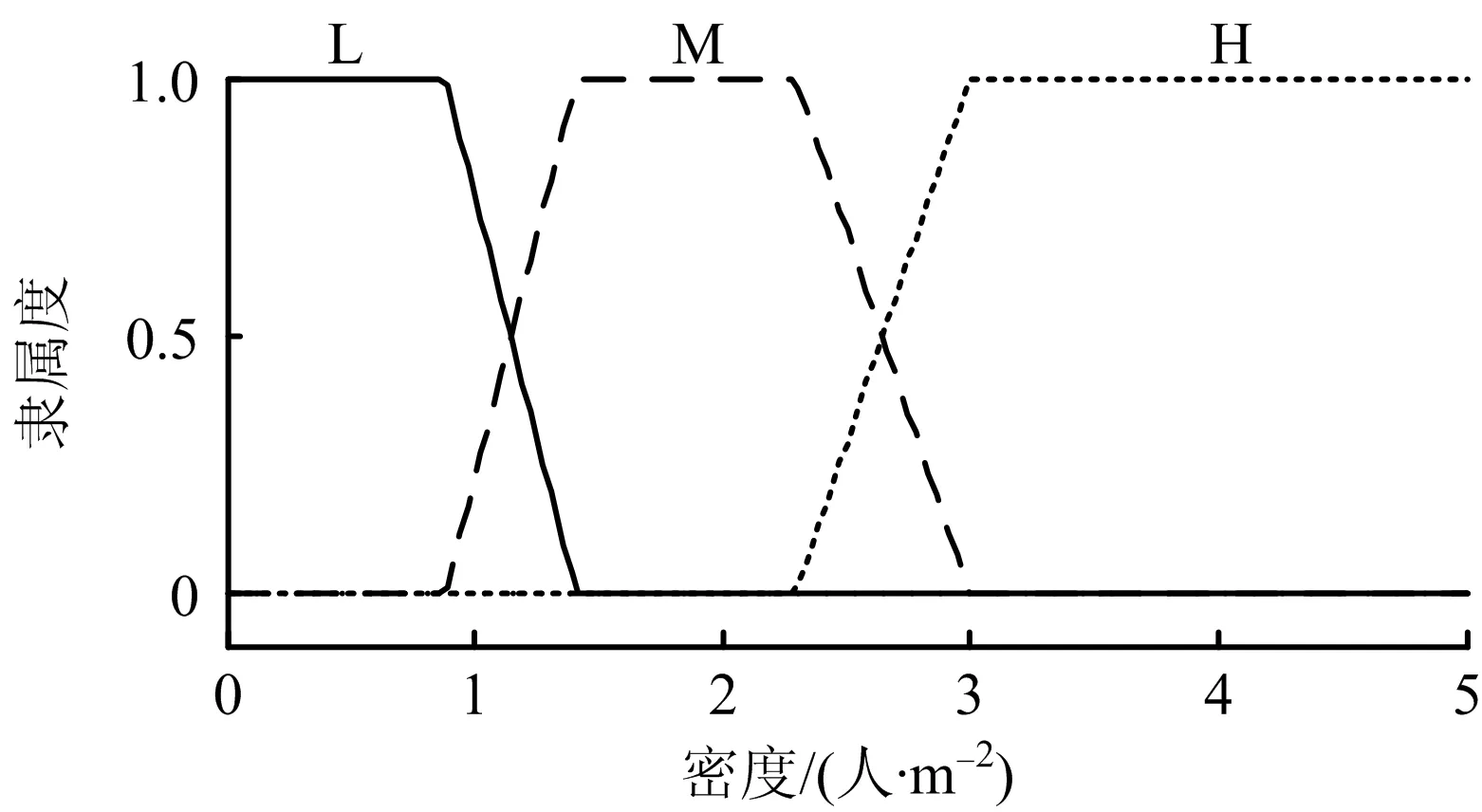
图3 障碍物密度隶属函数Fig.3 Membership function of obstacle density
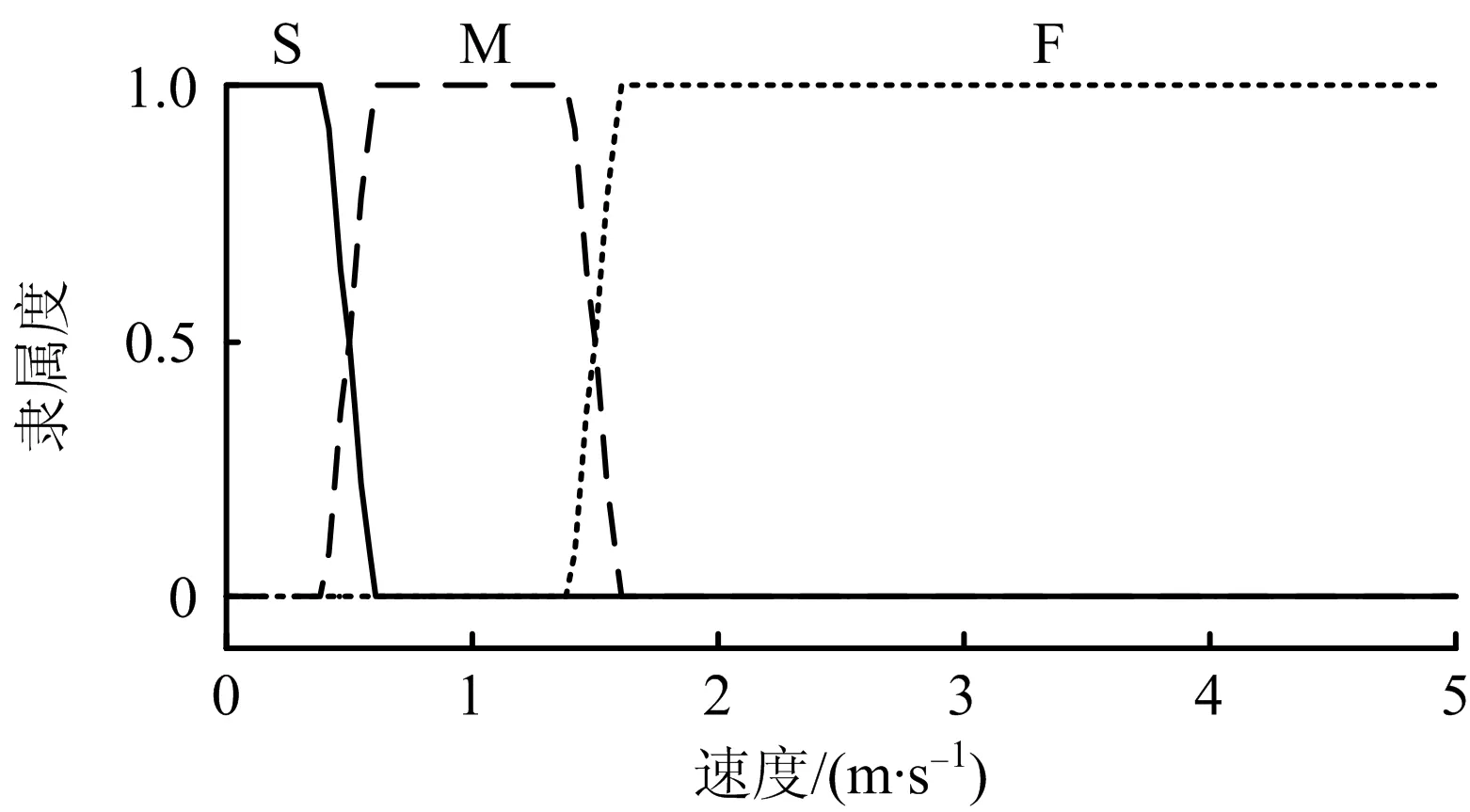
图4 速度隶属函数Fig.4 Membership function of speed
行人在向目标方向移动的过程中,根据感知到的环境信息,将与最近障碍物的距离和障碍物密度加权融合,确定运动速度。行人与最近障碍物的距离越大,移动速度越大;障碍物密度越小,移动速度越大。但是当行人与最近障碍物的距离非常近(<0.4 m)时,即使目标方向上的障碍物密度很低,行人的移动速度依然为0。因此,为避免决策冲突,设定行人间最短距离与人群密度的权重之比为0.7∶0.3。模糊推理系统可以描述为式(1):
[V]=R(D,E)
(1)
式中:V表示行人移动速度,m/s;R()为模糊推理系统函数;D表示行人与最近障碍物的距离,m;E表示感知范围内的障碍物密度,人/m2。推理规则见表1,共包含9条规则。

表1 模糊推理规则Table 1 Fuzzy inference rules
2)基于BFS算法的危险度模型的建立
行人向安全出口的移动通过元胞的危险度确定。危险度越低,行人向该格点移动的概率越大。危险度主要由格点与出口间的距离(“静态危险度”)以及出口附近的人群密度(“动态危险度”)2个因素决定。
从疏散开始到结束,行人a在单位时间Δt内从m(m>1)个出口中选择出口i的概率Pi如式(2)所示:
(2)
其中Q的计算如式(3)所示:
(3)
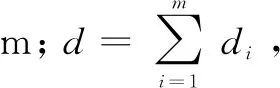
静态危险度采用广度优先遍历(Breadth-First Search,BFS)算法计算。BFS是1种解决图论中最短路径问题的遍历算法[14],其基本思想是采用逐层扫描的方法,从起始顶点开始依次访问其每1个邻接点,然后以邻接点为顶点继续扫描下1层邻接点,直到到达路径的终点或设定的终止条件为止。BFS在逐层遍历图时用队列存储邻接顶点,利用队列的“先进先出”实现遍历要求[15]。
静态危险度由格点与出口的距离决定,以出口为中心,向周围递增,离出口越近,危险度越低,离出口越远,危险度越高。静态危险度BFS算法流程如下:
①将所有方格的危险度记为DI。


④如果扩张元胞与当前格点同属于当前出口内的格点,那么该扩张元胞的预期危险度为0,否则,扩张元胞的预期危险度为当前格点的危险度与Dxy之和,Dxy的计算如式(4)所示:
(4)
式中:Dxy为元胞为扩张元胞(x,y)与当前格点的距离,m;Me为无限大的正数,说明障碍物格点的危险度为无穷大,行人不会选择被障碍物占据的格点移动。
⑤如果扩张元胞的危险度为所有方块的危险度DI,或者大于预期危险度,将其危险度设为预期危险度,并加入队列;如果预期危险度为0,将其加入队列头,否则加入队列尾。
⑥如果队列不为空,则返回步骤③,直到队列为空。
⑦如果还有未访问过的出口,则返回步骤②,直到所有的出口均已访问,且队列为空,算法结束,即可得到每个格点的危险度。
3)基于排队理论的出口疏散机制
疏散过程中拥堵主要集中于疏散出口处,行人在封闭区域中的疏散时间可视为自由流时间,到达疏散出口拥堵处开始排队疏散[16]。基于交通路网中的常见的Vickrey点排队模型,将疏散区域的拥挤延误转化为端点的排队时间。基于元胞自动机的传统BFS方法在出口处的疏散图如图5所示。假设当行人①准备离开出口时的速度为V1。当行人①离开出口后,周围的行人②~⑥均有可能移动到出口附近。此时按照本文提出的模糊速度模型,则周围的行人②~⑥会考虑周围的影响,因此最终某个行人会以速度V2移动到出口附近。根据文献[1]以及行人流的理论可知当出口处行人密度增加时,会导致行人移动速度降低,因此必然存在如式(5)所示的关系:
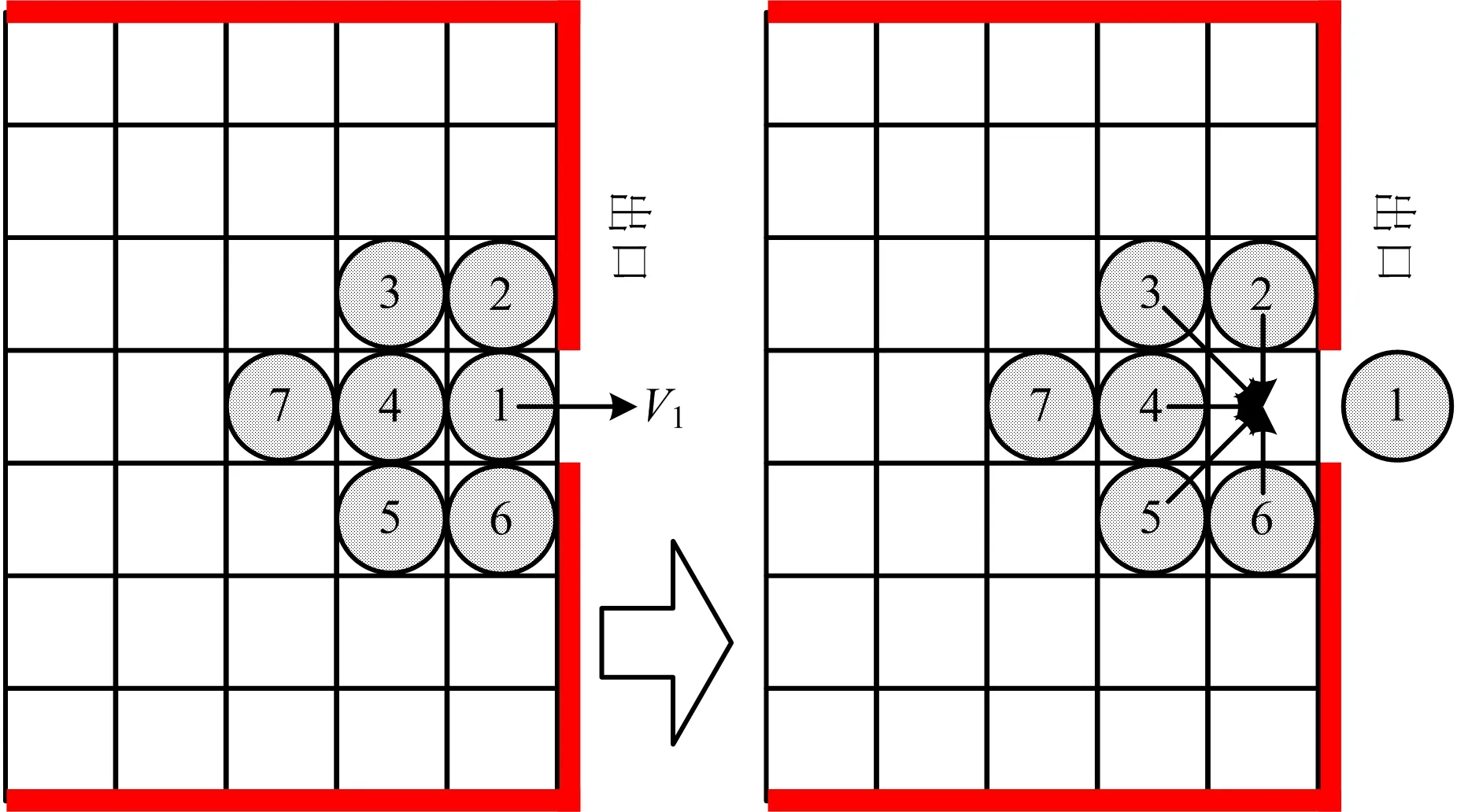
图5 传统模型出口疏散Fig.5 Exit evacuation diagram of traditional model
V2≪V1
(5)
这种情况下严重影响出口行人疏散效率。
为进一步提高疏散效率,为设施设备的优化布局提供实验依据,本文在模糊速度规则的基础上引入出口行人疏散排队理论。基于该模型,路径上同行能力不受限制,将疏散行人拥挤延误转化为端点的排队时间,排队理论模型过程如图6所示。
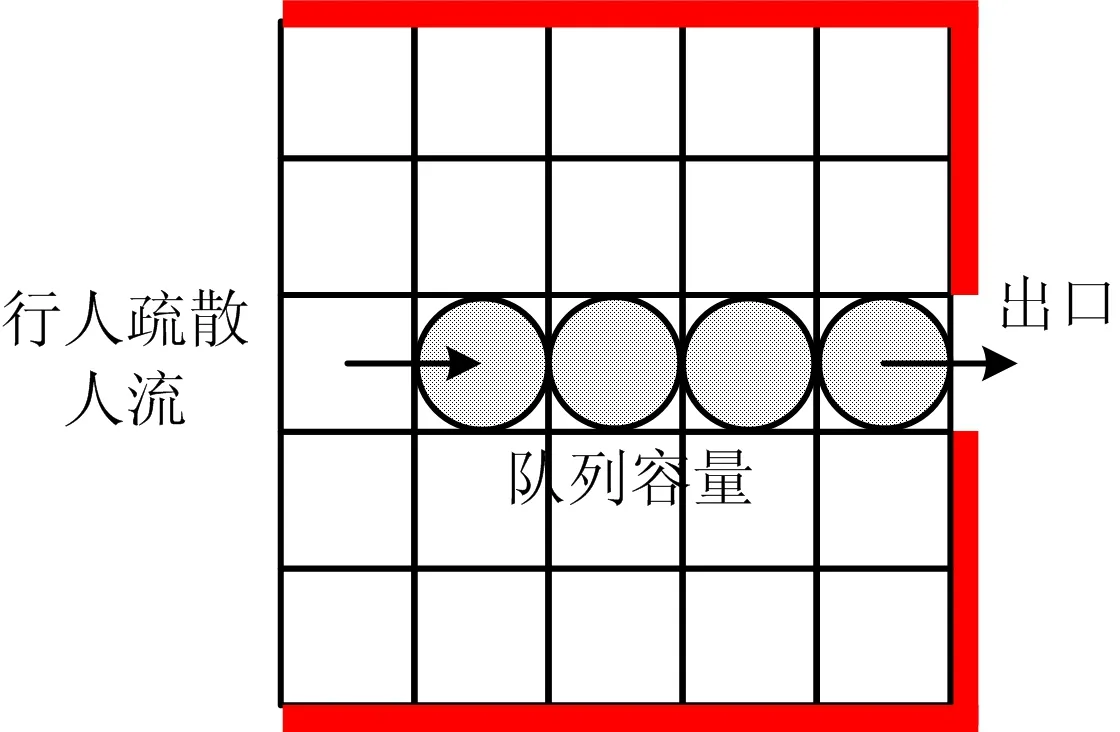
图6 排队理论模型Fig.6 Model diagram of queuing theory
根据图6的排队理论模型对图5的人员疏散进一步分析。基于排队理论模型的出口疏散图如图7所示。按照图7的疏散流程,当行人①以速度V1离开出口时,此时周围虽然有行人②~⑥,但是根据排队理论只有行人④可以顺利移动到出口位置。假设行人④移动到出口位置的速度为V3,则满足的关系如式(6)所示:
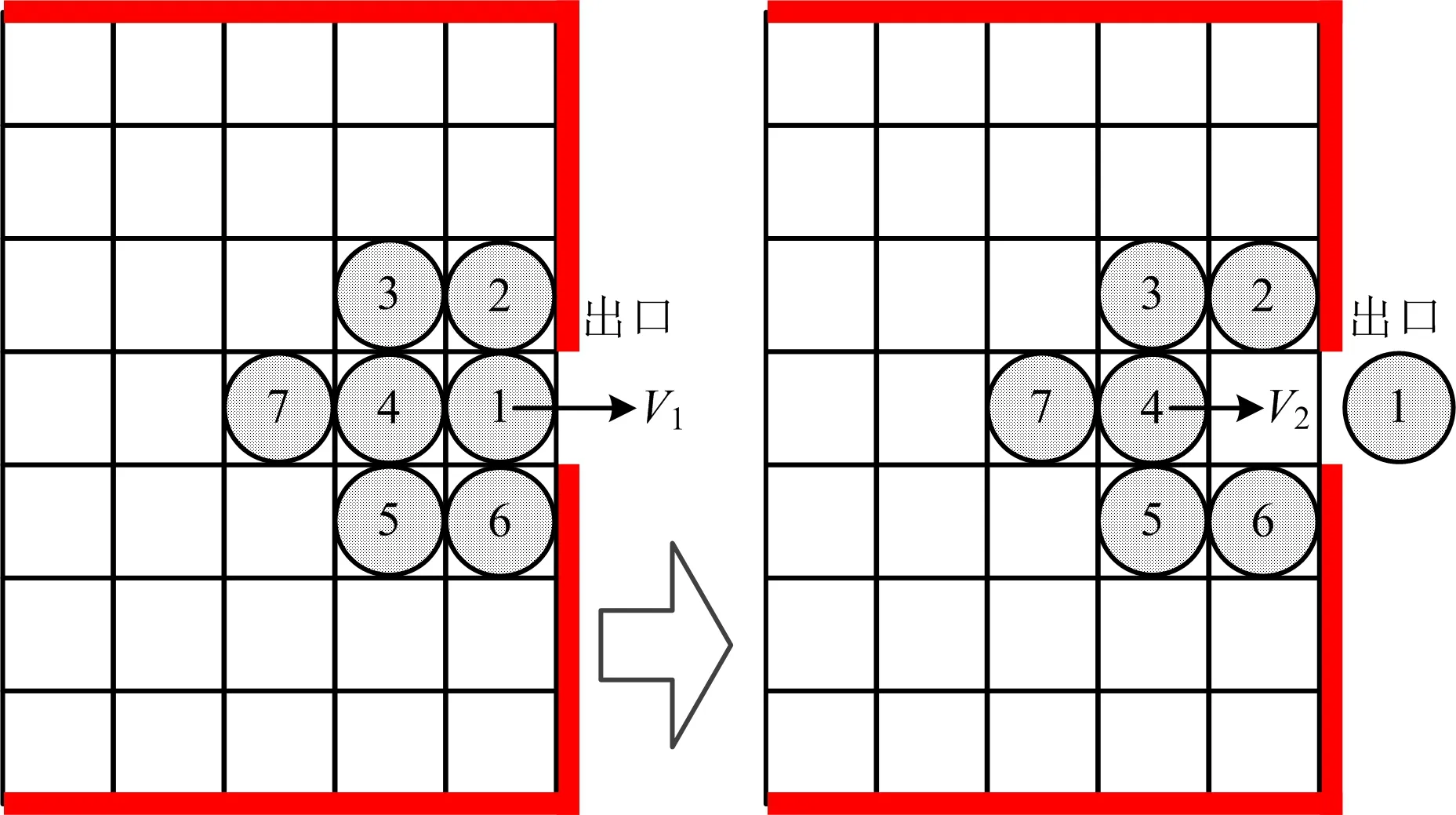
图7 基于排队理论模型出口疏散Fig.7 Exit evacuation diagram based on queuing theory model
V1=V3≫V2
(6)
根据以上分析可知,采用排队理论能够有效提高出口处行人的疏散速度。此时,利用疏散延时时间,行人③,⑤,②,⑥会依次进入疏散队列。基于排队理论的行人疏散策略如图8所示。定义图8中①,④,⑦,③所在位置区域为排队区域。行人按照队列依次高速离开出口。灰线与排队区域中间为排队调整区域。该区域的行人会自我调整,依次进入排队区域。疏散行人遵循先进先出( First Input First Output,FIFO) 原则。
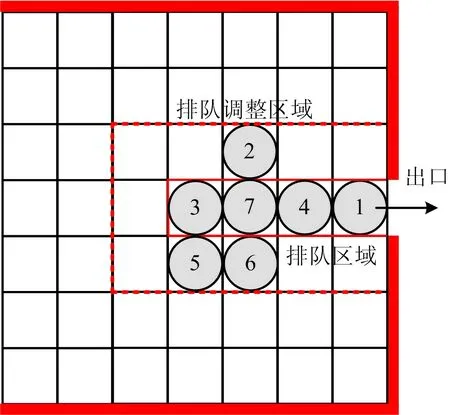
图8 基于排队理论的行人疏散策略Fig.8 Pedestrian evacuation strategy based on queuing theory
基于排队理论的行人疏散步骤如下。
步骤1:行人疏散移动进入排队调整区域。
步骤3:往出口反方向平行于排队区域移动。如果前方有行人则等待,否则移动。移动后判断是否满足步骤2中的距离要求,如果满足则排队离开出口,否则进入步骤4。
步骤4:继续往出口反方向平行于排队区域移动,直到满足距离要求。
2 仿真与分析
为验证本文所提出的元胞自动机模型的有效性,通过模拟仿真的方法进行应用分析。模型建立在空间大小为21×29的离散二维空间内,即把人群的移动空间分成离散的21×29个元胞。每个网格实际占据面积0.4 m×0.4 m,每个出口占据1个元胞,大小为0.4 m,每次只允许1人通过。疏散空间中共有198名行人,模拟行人的直径为0.4 m,行人中心为格点的中心。如图9所示。图9为根据仿真条件设计的含有2个出口的疏散环境,出口A位于疏散空间的左下方,B位于上方。行人初始行走速度为0.9~1.5 m/s,正常状态下的速度为1.25 m/s,应急疏散情况下期望速度大小为2.5 m/s。模型采用并行更新机制。为使数据分析可靠有效,所得数据为8次模拟的平均值。

图9 疏散环境平面Fig.9 Plan view of evacuation environment
2.1 改进模型仿真分析
根据本文所提出的模型,疏散过程如图10所示。图10(a)~(f)分别表示t=10,20,30,40,50,60 s时,行人的疏散情况。行人考虑与出口的距离和出口附近的人群密度,向危险度较低的出口移动。由图10(a)可知,在疏散的初始阶段,由于距离B出口的人数较多,所以根据最近距离原则,选择B出口的人数较多。随着疏散过程的继续,B出口的行人越来越多,人群密度增大,移动速度降低,导致排队时间增长。这时行人会综合考虑“静态危险度”和“动态危险度”的值,重新评估通过2个出口的总时间,选择总时间较少的出口。因此部分行人改变目标出口,朝A出口疏散。由图10(f)可以看出,通过2个出口的人员几乎同时离开疏散区域,符合实际疏散情况。行人在疏散过程中向出口聚集时,出口区域呈现“拱形”结构,在疏散后期“拱形”结构逐渐变小并最终消失。模型仿真再现行人疏散的自组织现象,证明所提出模型是有效的。

图10 行人疏散仿真过程Fig.10 Simulation process of pedestrian evacuation
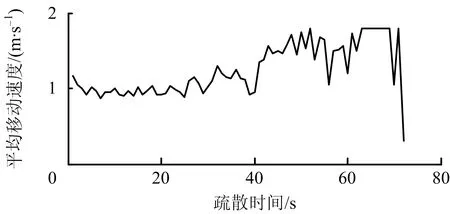
图11 基于模糊速度规则的行人平均疏散速度曲线Fig.11 Average evacuation speed curve of pedestrian based on fuzzy speed rules
(7)
在本文提出的模型中,每个行人根据周围环境以不同的速度方式移动,随着疏散的进行,当t>40 s时,疏散区域中人数变少,人群密度降低,平均疏散速度增加。当t为56 s左右时,平均移动速度急剧下降。这是因为在疏散的后期,区域内大部分行人出现在“拱形”区域内,行人之间密度很小,导致平均速度下降。疏散区域内所剩行人继续减少,行人的移动速度随之增加,并达到最大值;当行人全部离开疏散区域时,行人移动平均速度降到最低。平均疏散速度的提高在一定程度上提高疏散效率。
2.2 与传统元胞自动机疏散模型对比
1)与传统疏散模型的对比
①移动速度
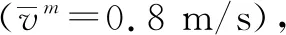
②出口方向选择
传统疏散模型和本文所提出的模型在出口方向的选择上,均考虑行人所在位置距出口的距离和出口处人群密度2个影响因素,其中静态危险度均采用BFS算法计算。
③出口疏散机制
本文提出基于排队理论的出口疏散机制,而传统模型中未包含此部分。
2)疏散时间与效率对比
在A,B 2个出口的疏散环境下,2种模型的疏散时间对比情况如图12所示。可以看出,传统模型的疏散时间为t=87 s,改进模型的疏散时间为t=72 s。较之传统模型,改进模型的疏散时间缩短15 s,疏散效率提高17.24%。
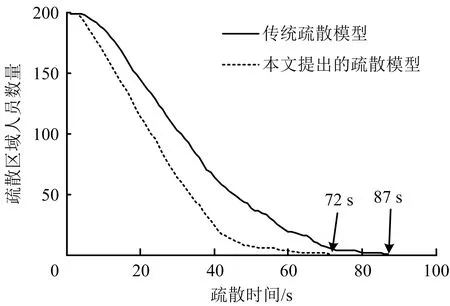
图12 疏散时间对比曲线Fig.12 Comparison curve of evacuation time
3)出口利用率对比
传统疏散模型和本文提出的疏散模型在整个疏散过程中,各出口的疏散人数随时间的变化情况如图13所示。横坐标X表示疏散时间,s,纵坐标Y表示疏散人员的数量,个。传统模型中出口A和B的疏散人数分别是68和130,本文提出的模型在出口A和B的疏散人数分别为96和102,相比于传统模型,2个出口的疏散人数更加接近,出口利用率更高。
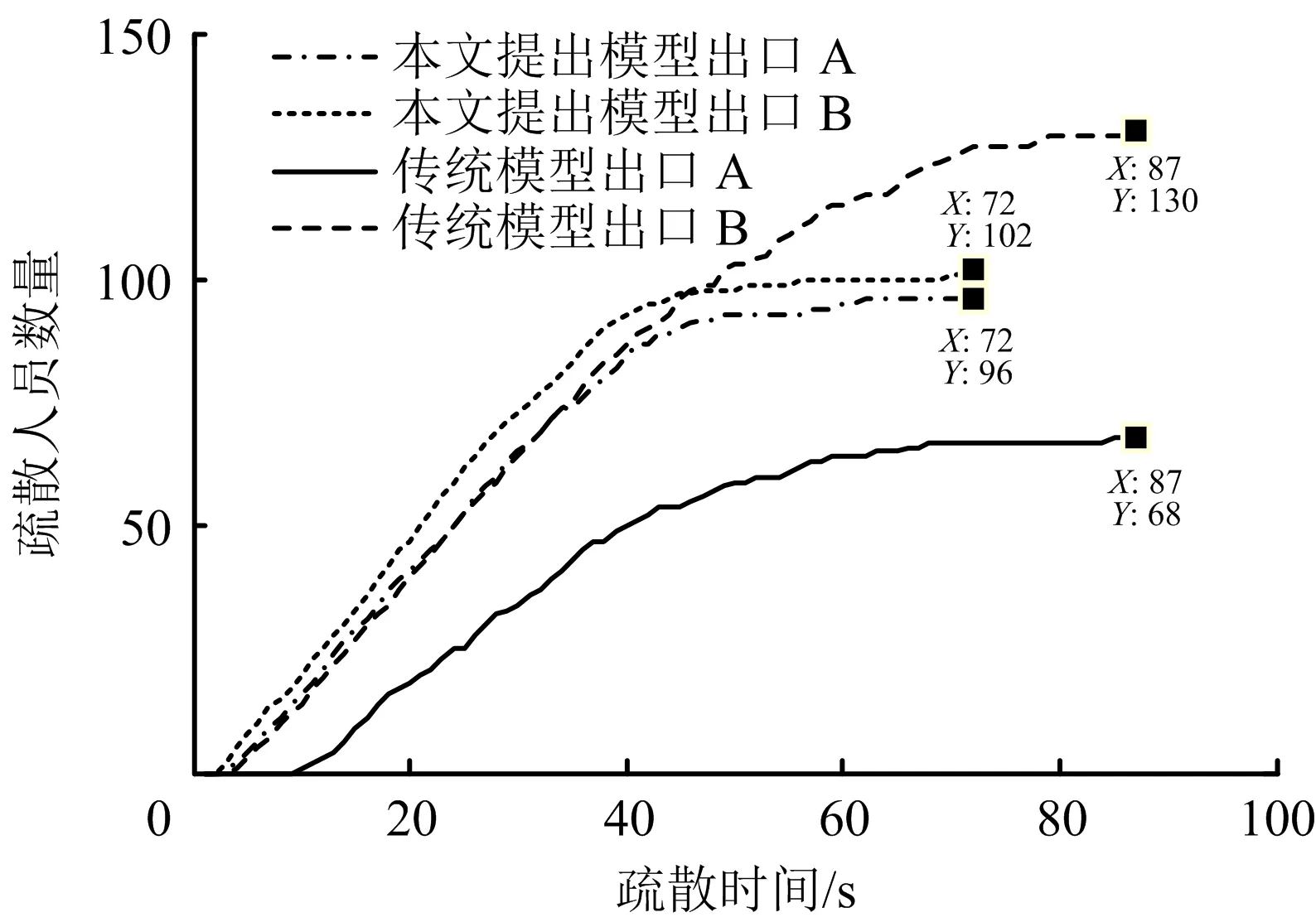
图13 不同出口的疏散人数对比曲线Fig.13 Comparison curve of number of evacuees at different exits
虽然2个模型在计算危险度时均考虑行人位置与出口的距离和出口附近的人群密度,并将二者进行耦合,但传统模型2出口的疏散人数之差仍然较大。原因是行人的疏散时间由行人移动到出口的时间(自由流时间)和在出口排队疏散的时间(排队时间)2部分组成。在传统模型中,对于B出口疏散区域的外围人员来说,当B出口人群拥挤而以A为目标出口时,行人只能以1元胞/步的速度向A出口移动,这时移动到A出口所花费的时间与继续选择B出口所花费的时间相比并未减少,因此行人继续选择从B出口疏散。改进的模型中,行人能够根据周围环境调整移动速度,比如当B出口疏散群体的外围行人在朝向A出口的前进方向上无行人阻碍时,能够以较大的速度向A出口移动,使从A出口疏散的总时间少于继续从B出口疏散的时间,从而以A为目标出口。因此本文提出的模型能够解决多出口环境中行人的出口选择这一重要问题,更真实地描述行人的决策过程与疏散行为,更符合真实的疏散情况。
3 结论
1)根据行人对周围环境的模糊感知,运用模糊推理理论建立动态模糊速度模型,从微观角度更加真实准确地描述行人不同的移动速度,以及群体疏散过程,为行人疏散模型的建立提供1种思路。
2)通过设定危险度规则,使用基于双端队列的BFS算法快速计算每个格子的危险度,同时结合出口附近的人群密度,更加科学合理地选择安全出口,规划疏散路径。
3)在出口疏散方面,引入排队理论模型,设置排队区域和排队调整区域,优化排队模式,进一步提高疏散效率,为公共区域的设施布局提供有效建议。

