WPA-IGA-BP神经网络的模拟电路故障诊断
王 力, 刘子奇
(1.中国民航大学职业技术学院, 天津 300300;2.中国民航大学电子信息与自动化学院, 天津 300300)
0 引 言
目前,模拟电子电路大量应用于航天、军事、通信和其他各个领域的电子系统中。统计数据表明,在绝大多数混合电路中,模拟电路的故障发生率超过80%。但是,针对模拟电路的故障诊断方法却十分落后,难以应对目前模拟电路大范围的应用[1-3]。
模拟电路的电路故障一般分为结构性故障和参数变化型故障。结构性故障是电路发生很大的破坏,使得电路无法完成其基本功能;参数变化型故障是指电路元器件参数的实际值超出了容差范围,使得电路工作的性能发生改变[4],难以提取故障特征。文献[5]提出利用复数域模型对模拟电路进行故障特征提取,易产生较多模糊集。文献[6]提出一种针对线性信号的特征提取方法,而模拟电路中更多的是非线性信号。文献[7]提出极限学习机的思想,但是特征提取过程较为复杂。文献[8]提出利用贝叶斯技术进行故障诊断,但是该方法没有将任何物理过程纳入计算,使其不适合进行长期诊断,从而使得分类的准确度降低。文献[9-10]提出利用故障树诊断模型。文献[11-16]提出利用支持向量机以及优化算法来实现故障诊断,但单核的支持向量机容易忽略输入样本中的有用信息,难以达到最优泛化能力。在采用多核优化后,能够达到较好的诊断效果,但算法较为复杂,训练速度慢,难以快速诊断。文献[17]提出利用粒子群算法优化支持向量机。文献[18]提出利用粒子群算法优化反向传播(back propagation,BP)神经网络来解决BP神经网络易陷入局部最优的问题。文献[19]提出利用遗传-粒子群算法来解决BP神经网络中存在的结构设置复杂、寻优速度较慢、容易陷入局部最优解等问题,但是遗传算法(genetic algorithm, GA)和粒子群算法相似,具有盲目性,当再次诊断时需要重新训练。文献[20]提出利用密度峰聚类和动态权值优化BP神经网络,解决了其收敛速度慢和准确度低的问题。文献[21]提出免疫遗传优化算法,具有快速反应且能够利用GA消除局部最优等优点。
综上所述,现有研究成果采用的验证电路,几乎全部为滤波电路。而针对模拟电路中的放大电路缺少理论及实验验证。本文针对模拟电路中放大电路的渐变性软故障,提出一种基于免疫遗传优化BP神经网络的模拟电路故障诊断方法。首先,通过对电路原理图的仿真分析,明确故障类型并进行故障仿真,提取故障数据。其次,利用小波包分析方法,对故障数据进行特征提取作为算法的输入。最后,采用免疫GA-BP(immune GA-BP, IGA-BP)神经网络算法进行故障诊断。选取广泛应用的基本分压放大电路验证所提方法的效果。
1 基于小波包的故障特征提取
在模拟电路的渐变性故障诊断过程中,获得故障数据并进行特征提取尤其重要[22]。小波分析在处理脉冲响应信号、获取小波量为特征向量方面获得了广泛的认可。本文利用小波包的分解和重构最终得到归一化的故障特征向量[22-23]。
1.1 小波包分析
小波包分析是由小波分析发展而来,小波分析针对高频函数信号,处理能力还有局限。但是小波包对信号的分解是没有冗余和疏漏的,对采样的低频信号部分和高频信号部分能够作频率分析以及时间分辨率的分析[24]。在模拟电路的信号采样中,输出信号各个频带的能量变化的改变揭示了模拟电路中部分元件是否损坏,在进行模拟电路故障诊断时,小波包能够把模拟电路元件的好坏情况与模拟输出响应中各频率层的能量值的改变进行比较,可以更好地进行故障的特征提取。
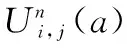
(1)
式中,n为振荡次数;i为尺度坐标;j为位置坐标。当且仅当n=0,1;i=j=0时,初始小波包函数定义为
(2)
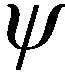
(3)
故式(3)定义的函数集合{Un(a)}(n=0,1,…)就是关于正交尺度函数φ(a)的小波包。
小波包分析分为分解与重构两个过程。小波包分解过程如下所示。
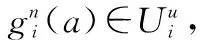
(4)
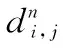
(5)
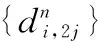
(6)
小波包分解将信号分解为某一尺度下的低频系数和高频系数,再改变尺度继续进行更精细的划分,最后得到频率范围相等的2n个频段。小波包分解树状图如图1所示。
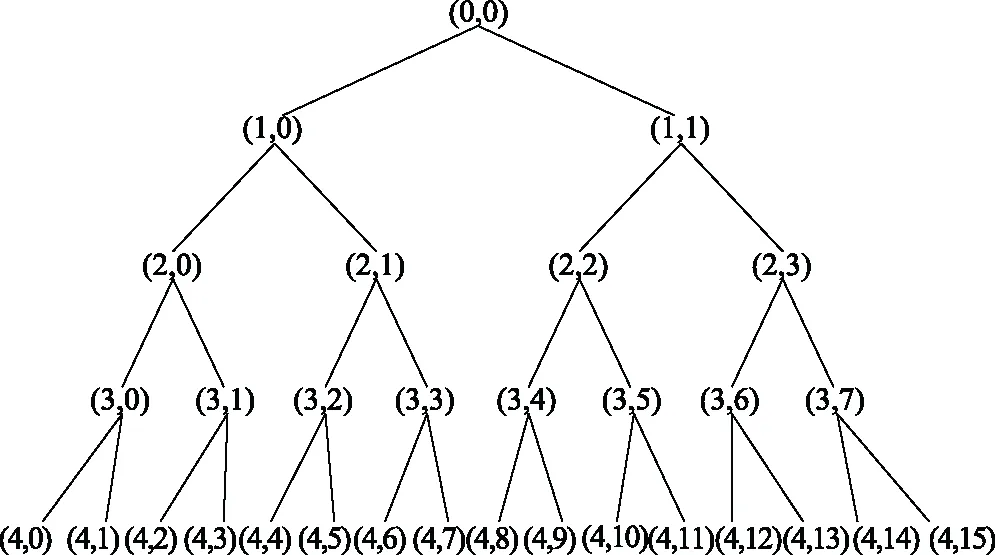
图1 4层小波包分解树状图
1.2 提取特征向量
当输出响应发生变化时,各个状态的输出响应信号的能量值也会有明显的变化。所以,通过进行小波重构,计算不同频带下的波形能量,每一频带有16个子频带,对应16个能量值,进行归一化处理后形成故障状态所对应的特征向量。具体步骤如下。
步骤 1计算小波包分解最后一层各频带的能量,而后计算各子频带信号的能量:
(7)
式中,E4i为第4层小波包分解子频带i的能量值;j为第4层第i个子带的离散点;xi j为幅值。子频带能量值如图2所示。
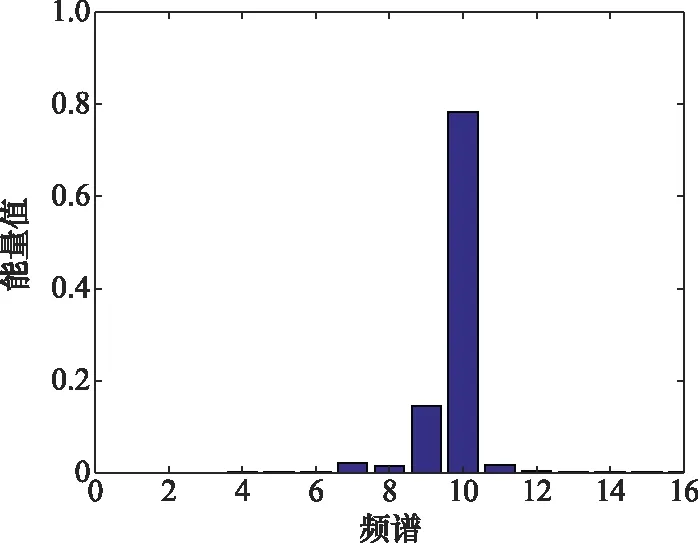
图2 子频带能量值
步骤 2计算第4层子频带的总能量E4:
(8)
步骤 3归一化处理,用ci取代能量归一化后的特征值:
(9)
步骤 4构造模拟电路故障诊断输出波形能量的特征向量C:
C=(c0,c1,…,c15)
(10)
2 遗传免疫优化BP神经网络
2.1 BP神经网络
BP神经网络的组成,如图3所示。
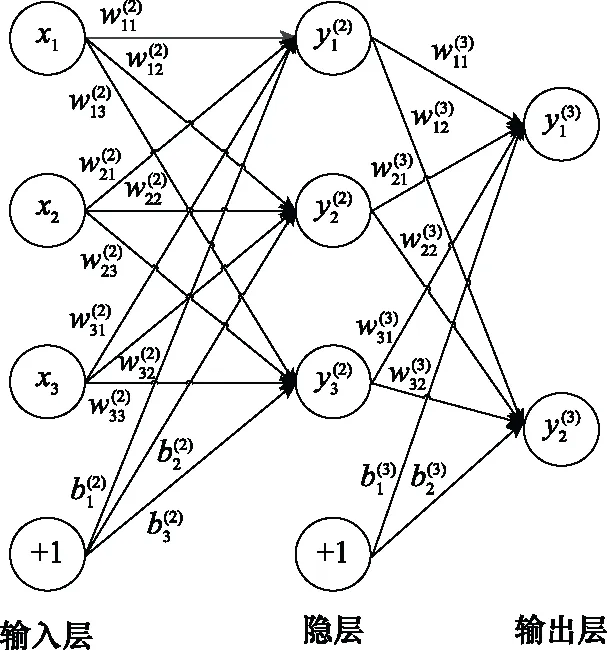
图3 3层神经网络结构图
前向传递时,将原始特征向量输入至神经网络的输入节点,经过神经网络中的隐层间传导,最后输出了计算后的结果向量。在后向传递时,根据设置误差修订权值和阈值,经过多次学习、训练和修订,得到最优的权值和阈值解,最终得到算法模型。
BP神经网络算法的关键点是计算权值w以及调整量Δw(n),计算Δw(n)从神经元i的输出端误差信号ei(n)开始。所以,根据神经元的位置分为两种不同的情况计算。
(1)当神经元i为输出节点
(11)
式中,η为BP神经网络的学习率[25];ε(n)为输出层y(n)之间的最小乘二。局部梯度δi(n)定义为
(12)
(2)当神经元为隐层节点
(13)
(14)
目前3层BP神经网络已被广泛应用于各个领域,而且能够很好地处理非线性函数的问题。但是,BP神经网络也存在各种缺点,主要有以下3类:① 由于学习速率是一开始设定好的,所以需要有较长的训练时间;② 由于BP神经网络算法主要通过梯度下降进行寻优,特别容易陷入局部最优的困局;③ BP神经网络在第二次使用时依然要从头训练和学习,步骤繁琐[26]。
2.2 免疫遗传优化算法
免疫算法(immune algorithm,IA)是模拟人体免疫系统对抗病原体入侵的过程,是IA与GA优势互补相结合,将IA中抗体和抗原的对应原理以及抗体多样性和抗体记忆的功能融合进入GA,形成IGA。其关键步骤如下。
步骤 1相似度计算
在IGA中,首先需要设定一个可以展示每个个体之间的差异值来观察种群的多样性,从而可以保证种群变化后的多样性,一般采用信息熵H(N)来表达个体之间的多样性的差异和区别[27]:
(15)
式中,Hi(N)为第i个样本的信息熵,定义为
(16)
式中,Pji表示第j(j=1,2,…,S)个与设定标准一致,在基因座i上的概率,即
(17)
式中,M表示在基因座i上出现的第j个设定标准一致的总个数。种群的相似度表示不同样本之间的接近程度,可表示为
(18)
式中,A(N)越大,种群多样性越小;反之,种群多样性越大。
步骤 2抗体浓度计算
抗体浓度可表示为
(19)
式中,T表示与抗体i相似度大于A(0)的所有抗体数总和。找出浓度值大于设定阈值L0的个体,其总数为N,那么这些抗体的浓度概率为
(20)
其余n-t个抗体的浓度概率为
(21)
式(20)和式(21)表明,浓度大于L0的抗体的数目越多,这些抗体的浓度概率越小;当抗体的浓度值都不大于L0,即t=0时,所有抗体的浓度概率均为1/N,表明抗体种群的多样性较大;当抗体的浓度值都大于L0,即t=N时,这些抗体的浓度概率将会变为0,说明抗体种群的单一性很高。
步骤 3繁殖概率计算
根据适应度Pf和浓度Pd计算繁殖概率:
P=λPf+(1-λ)Pd
(22)
式中,λ(0<λ<1)为亲和系数。当λ的数值较大时,适应度大的抗体有更大的概率将自己的基因传给下一代;当λ的数值较小时,适应度的影响减小,抗体浓度对繁殖概率的影响增大。因此,亲和系数的选取对基因的选择影响较大,需要根据优化的实际需要和程序执行情况进行调试。
相比于GA,IGA不仅能够防止算法进入局部极小值,而且拥有更好的全局搜索能力,同时保障了种群多样性,防止“早熟”现象的出现。其次,免疫记忆功能使得算法在第二次计算时,可以快速反应,加快测试速度。
2.3 IGA优化BP神经网络过程
首先建立BP神经网络结构,其中输入层为表达故障能量特征向量的神经元节点,数量为16;通过训练实验确定隐层节点数为8;输出节点数由具体电路的故障种类决定。将传统BP神经网络算法中固定的梯度下降参数寻优方法,替代为IGA的寻优方法,形成新的BP神经网络参数寻优方法,其关键的优化融合过程分为3个部分。
(1)抗原识别
在IGA中,首先就是要对抗原进行有针对性的辨别,一般是把BP神经网络的参数优化过程,转化成为一个求解权值和阈值的函数,然后再生成对应参数的随机解集,也就是IGA中所说的抗体,最后把优化的参数变量进行实数编码。
(2)适应度函数
本文中将训练样本的最小均方差作为适应度函数[28]。
(23)
式中,p为BP神经网络的输出;t为对应样本的期望输出;N为样本总数。
(3)遗传过程
首先进行交叉操作,根据基因选择概率Pd,从全部抗体基因中挑选两种抗体基因xa和xb,则两个抗体基因在基因座j位置上的交叉过程表达式为
(24)
式中,r是在[0,1]的系数。
其次进行变异操作,从编码的种群中随机挑选抗体个体,被选抗体上的编码以概率Pm进行单位变异。则抗体个体xa在基因座j位置上的变异操作表达式为
(25)
式中,yjmin和yjmax分别为第j位的极小值和极大值;r和r1均为[0,1]的随机值;q为当前进化代数;qmax为最大进化代数[27]。
优化算法的流程图如图4所示。
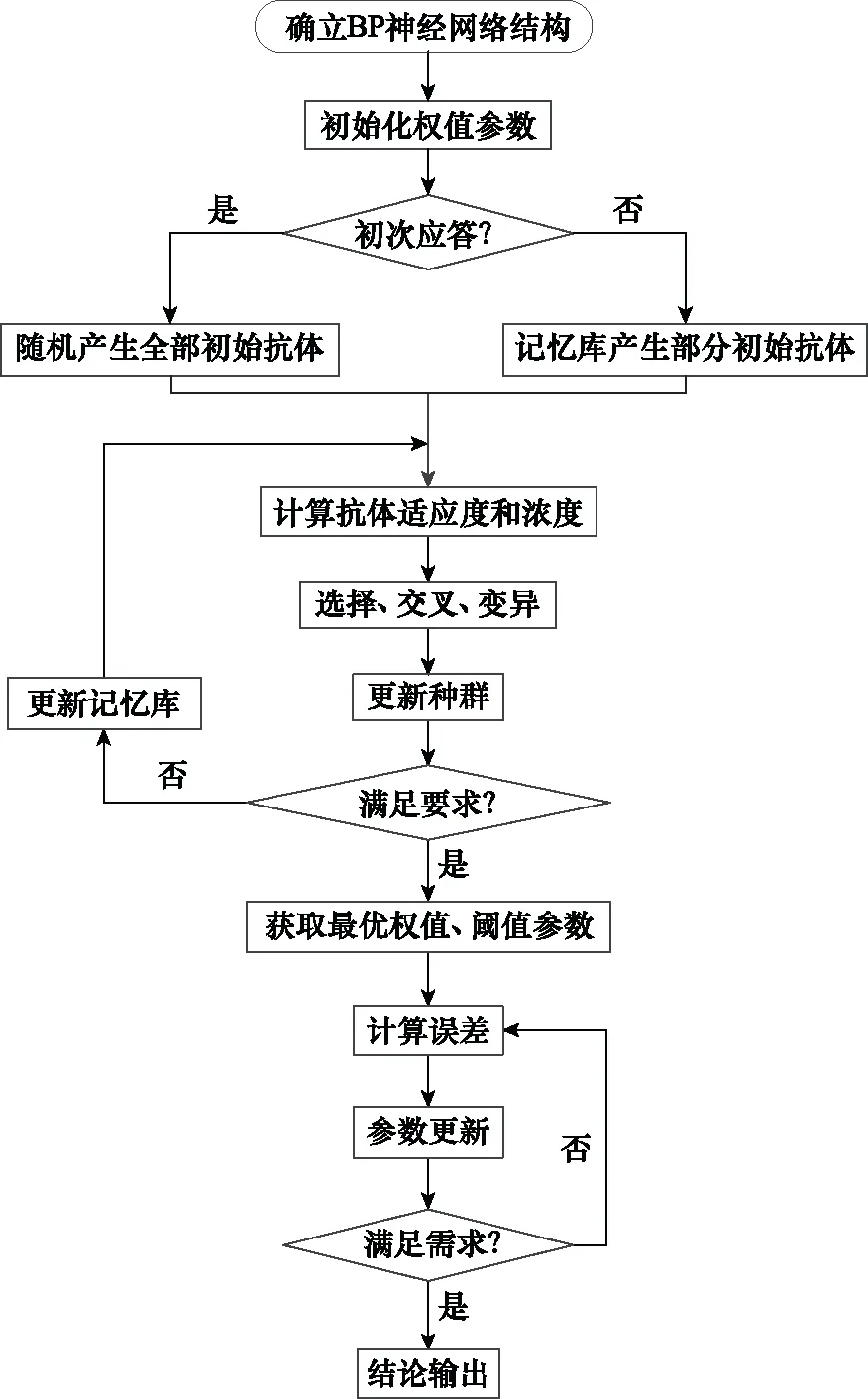
图4 优化算法流程图
具体步骤如下。
步骤 1初次识别:将BP神经网络中的参数进行抗原的初始识别,并设定算法的种群规模、记忆库容量、相似度阀值、交叉变异的概率等。
步骤 2是否为初次应答:若是,则随机产生初始个体种群;若不是,则从记忆库中产生初始个体种群。
步骤 3适应度评价:通过计算每个输入个体的适应度,判断个体与目标之间的距离。
步骤 4按照初始识别中设定的参数进行选择、交叉、变异等操作,更新种群信息。
步骤 5是否满足要求:若达到设定的要求或最大迭代次数,则结束循环并产生记忆单元;若没有达到设定要求,则在产生记忆单元后跳转到步骤3。
步骤 6当达到设定要求或者到达最大迭代次数时,开始寻找参数最优解,并记录最后的权值和阈值。
步骤 7进行训练并计算误差。
步骤 8判断是否满足误差要求,如果满足,则进行下一步;如果不满足,则更新神经网络参数并重新计算误差,循环至满足要求。
步骤 9输出故障诊断的最终结果。
3 诊断实验及分析
本文中的实验包括两个电路。第一个电路为基本分压放大电路,由于其主要功能以及输出信号为时域状态下的电压信号,故主要用于分析时域状态下故障特征提取及算法的诊断。第二个电路为标准电路中的四运放高通滤波器电路,主要用于分析频域状态下的诊断[29]。同时,由于四运放高通滤波电路较为复杂且元件较多,所以也可以验证所提方法在较大规模电路中的可行性。本文只针对单一故障进行诊断。
3.1 基本分压放大电路故障诊断
分压式基本运算放大电路结构如图5所示。
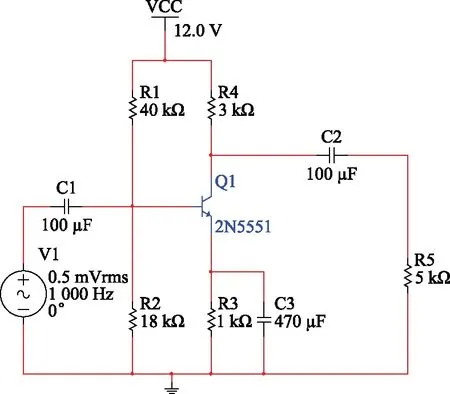
图5 分压放大电路原理图
图5中,各电路元件的正常状态值已经在图中给出,本实验设定电阻和电容的容差为5%。运用Multisim电路仿真软件,对电路进行参数扫描观察及灵敏度分析[30],找出可能会影响电路功能的元件,得到如表1所示的故障类型。
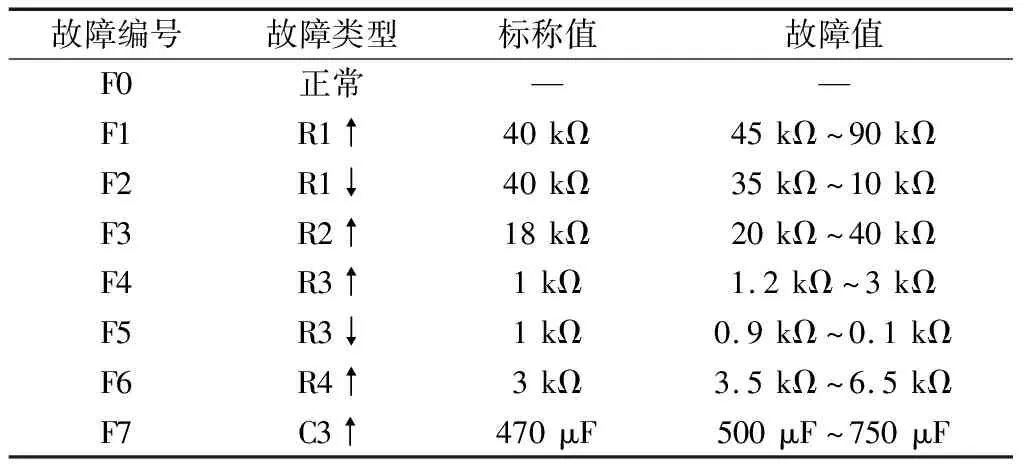
表1 分压放大电路故障标记
图6中给出了F2,F6和F7故障类型与无故障状态F0的输出电压曲线对比。
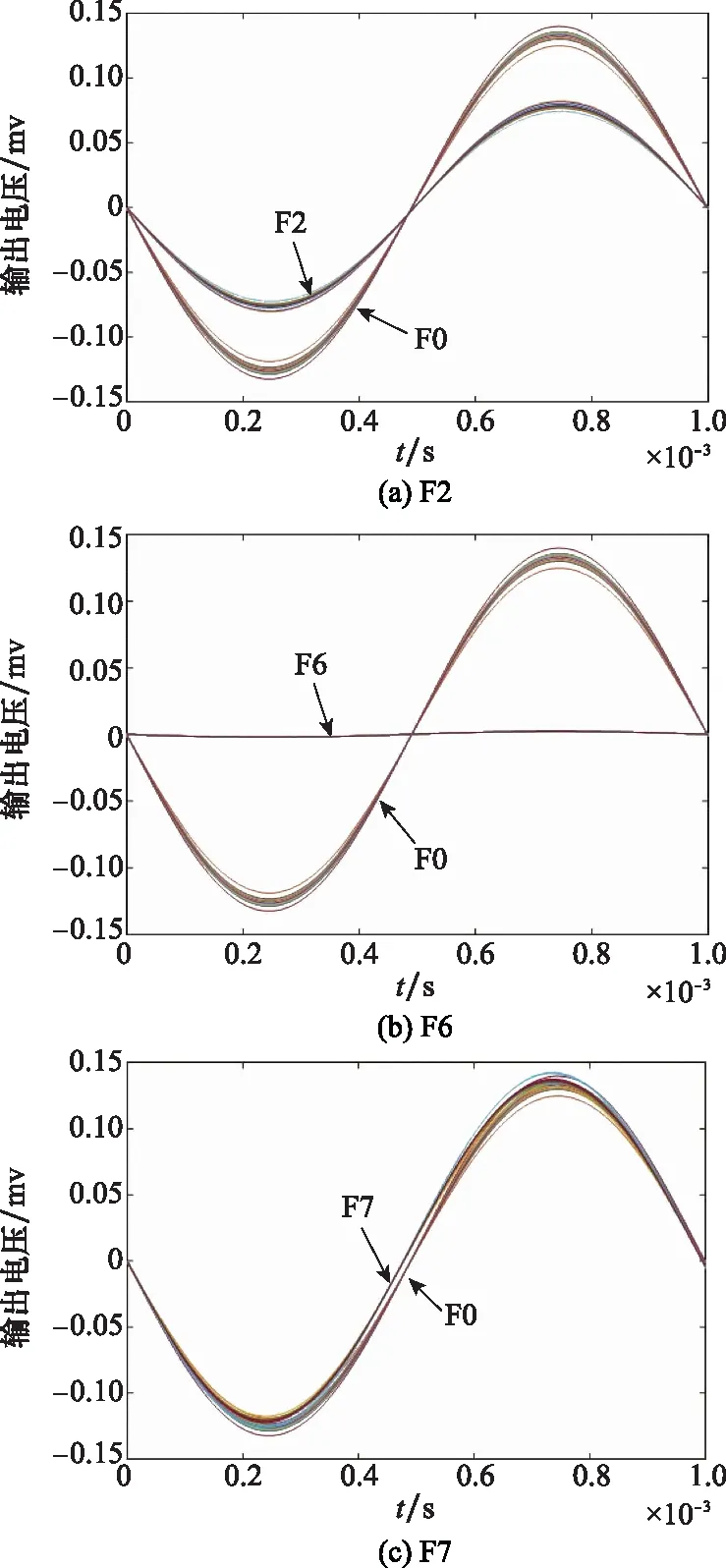
图6 3类故障状态下的输出响应
可以看出在这4类软故障中,F7与F0的输出电压曲线特性最为接近,两种类型的很多输出数值点存在重合,使得F7的诊断相对较难,而其他故障模式与F0均有较大差异。同时这也说明,F7所对应的故障元器件对电路整体性能影响较小。
对表1中7类有效故障进行参数扫描分析,得到70组不同故障状态,由于电路存容差,所以再将每组故障状态进行10次Monte Carlo仿真分析,共得到700个故障样本并将其分为两部分,第一部分(500个)作为训练样本集,第二部分(200个)作为测试样本集。
将电路仿真所得到的每一类故障原始样本(共700个)中的一个采样周期的输出电压信号进行4层小波包分解[24],每一个电压信号分为16个频带(S(4,i),i=0,1,…,15)的重构信号,小波类型采用db 6。利用之前提出的计算各个频段的能量比值作为特征向量的方法,进行特征提取并构造特征向量,故障特征能量谱如图7所示。
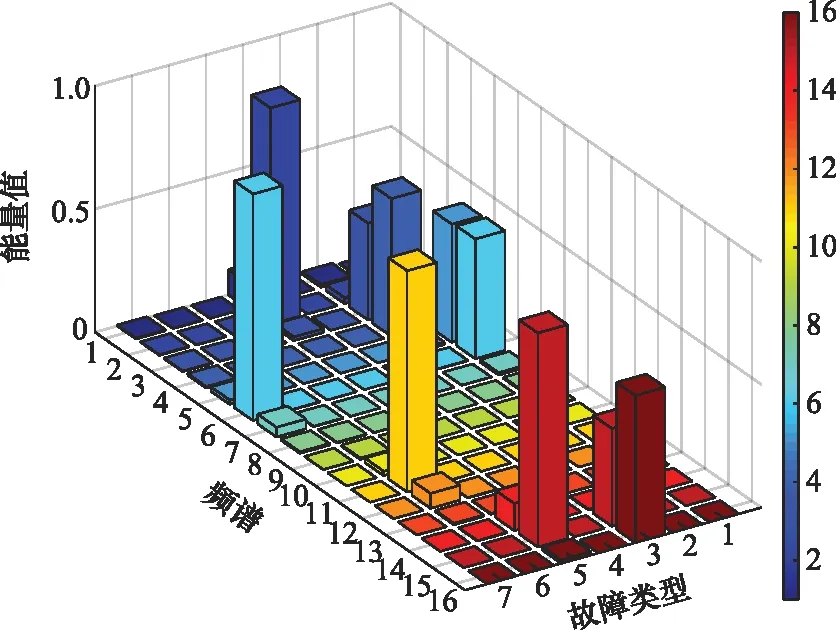
图7 实验1的能量频谱图
本次实验采用第2.3节中确定的神经网络结构,由于有8类(7类故障和1类正常)状态,则输出层节点数为8。其中IGA中设定交叉概率为0.5,变异概率为0.1,记忆库容量为15。先将500组训练样本特征向量进行标记并导入设定好的算法系统,对算法进行训练;然后将剩下的200组测试样本进行标记后[31]导入训练好的算法系统,便可得出诊断结果,如图8~图10所示。
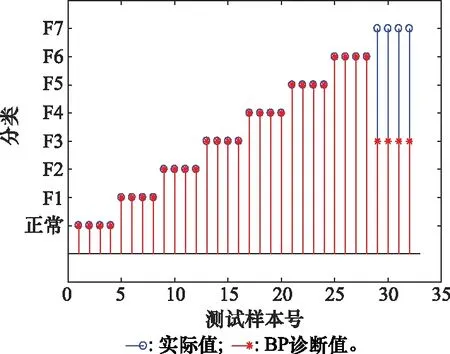
图8 实验1的BP诊断结果

图9 实验1的GA-BP诊断结果
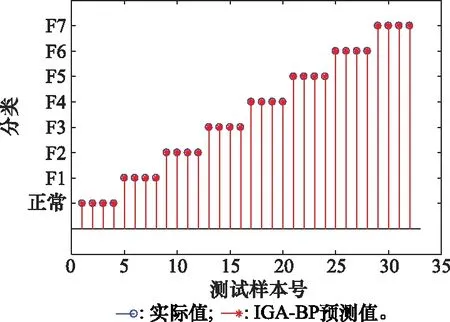
图10 实验1的IAG-BP诊断结果
最后,选择BP神经网络以及GA-BP神经网络,与本文所提IGA-BP神经网络进行对比实验。为了使其具有可对比性,采用相同的故障特征向量、相同的故障标记以及相同的训练集和测试集,得到的结果如表2所示。
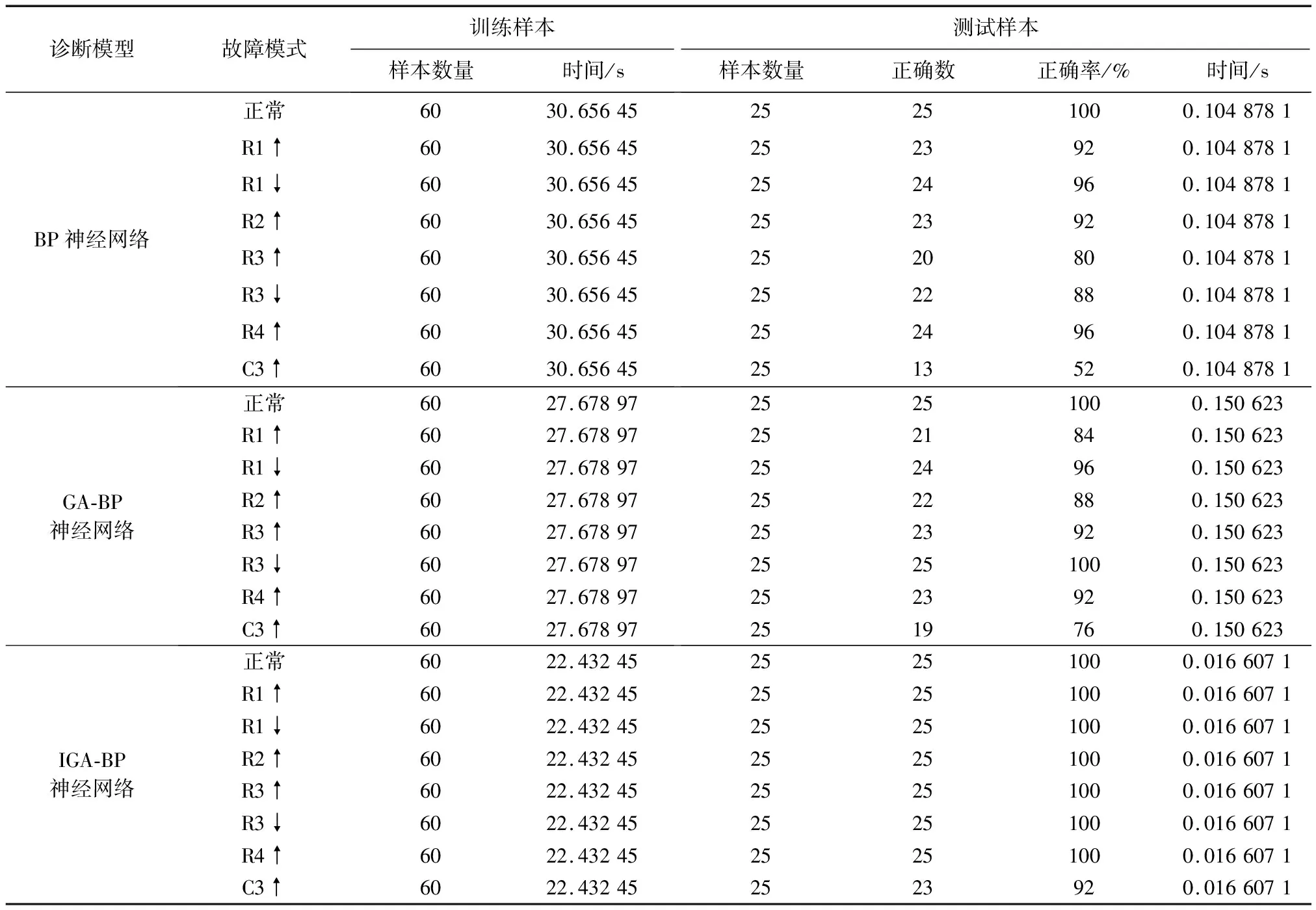
表2 实验1故障诊断结果对比
本实验表明在时间轴状态下,本方法可有效提取特征向量,并且通过横向对比,证明所提算法针对放大器及小型电路进行故障诊断时的准确度及测试时间均有较大提高。
3.2 四运放二阶高通滤波器电路故障诊断
四运放二阶高通滤波器电路如图11所示,各电路元件的正常状态值已在图中给出。本实验设定电阻和电容的容差为5%。运用Multisim电路仿真软件,对电路进行参数扫描观察及灵敏度分析,找出可能会影响电路功能的元件,得到如表3所示的故障类型。
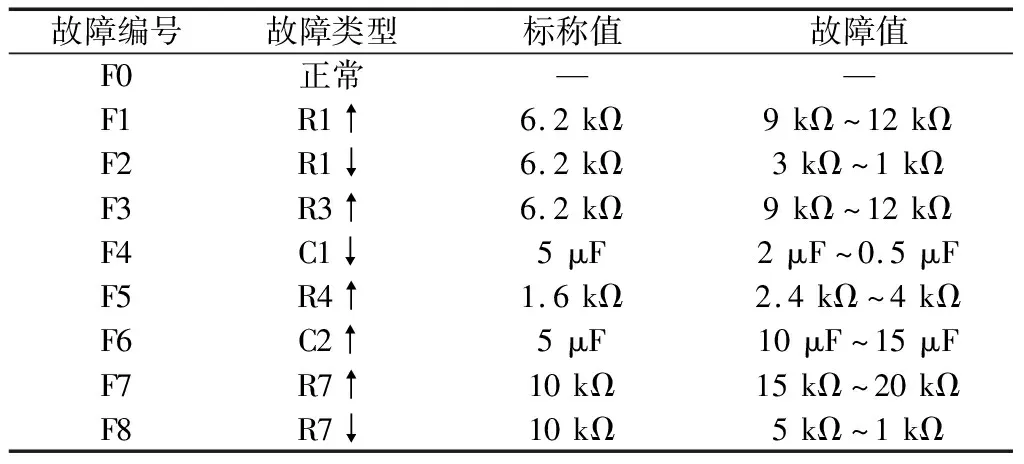
表3 四运放二阶高通滤波电路故障类型
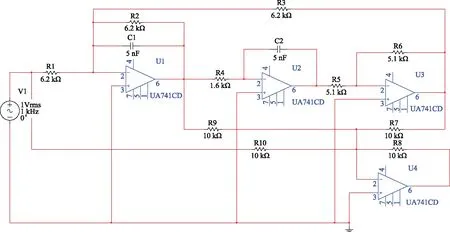
图11 四运放二阶高通滤波电路原理图
图12中给出了F1、F3和F5故障类型与无故障状态F0的输出电压曲线对比,所示故障中均与正常状态有较大差距,说明故障所对应元件皆对电路造成较大影响。图13中给出了F1与F7和F2与F8故障类型的输出电压曲线对比,从图中可以看出,波形相似且曲线存在较多重合点,区分这两类情况难度较大,不利于算法分类。同时说明R1和R7在发生故障时对电路输出造成的影响类似,对故障定位造成一定困难。
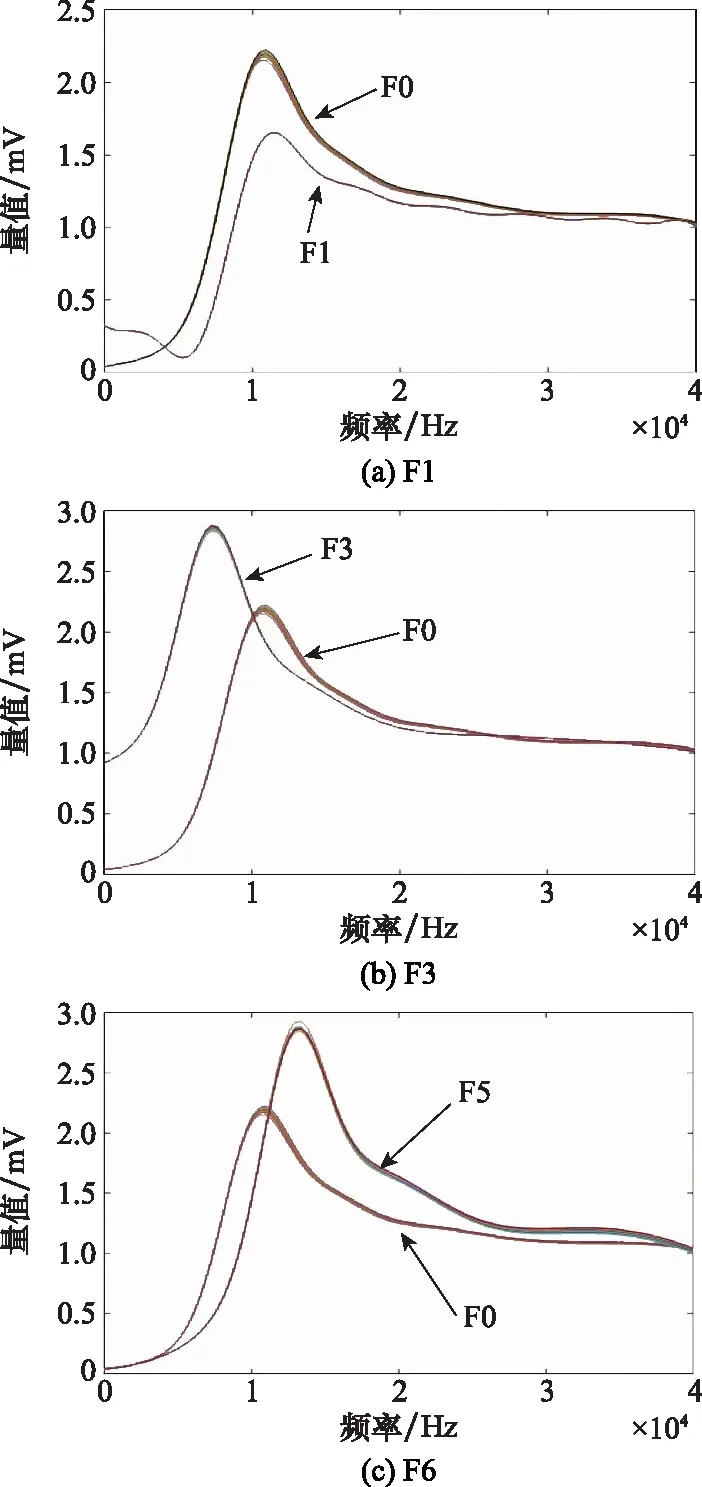
图12 3类故障状态下的输出响应
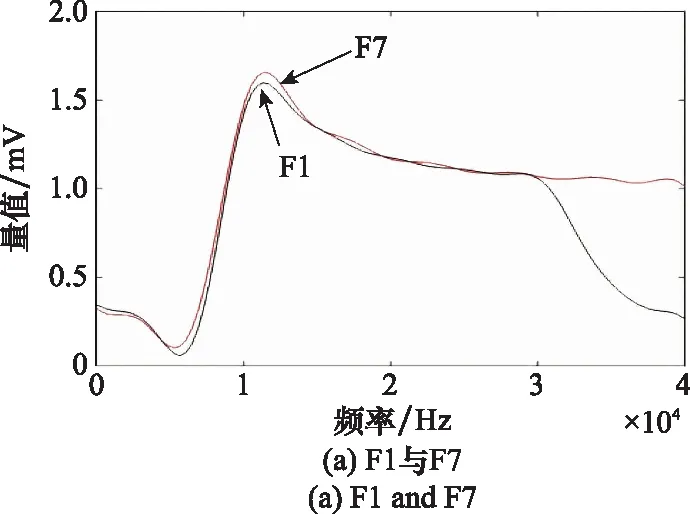
图13 F1与F7和F2与F8的输出响应
对表3中8类有效故障及正常状态进行参数扫描分析,得到90组不同故障状态,由于电路存容差,所以需要再将每组故障状态分别进行10次蒙特卡罗仿真分析,共得到900个故障样本并将其分为两部分,第一部分(600个)作为训练样本集,第二部分(300个)作为测试样本集。
采用与第3.1节中实验相同的方法得到故障特征能量频谱如图14所示。本次实验采用第2.3节中确定的神经网络结构,由于有9类(8类故障及1类正常)状态,故输出层节点数为9。其中IGA中设定交叉率为0.5,变异率为0.1,记忆库容量为20。先将600组训练样本特征向量进行故障标记导入设定好的算法系统,对算法进行训练,然后将剩下的300组测试样本经过标记后导入训练好的算法系统,得到诊断结果[31],如图15~图17所示。
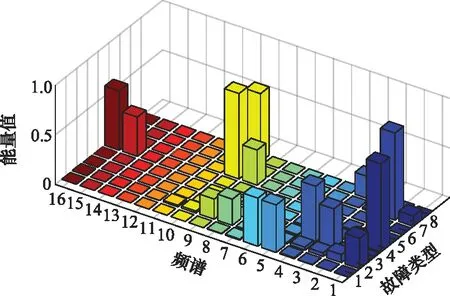
图14 实验2的能量频谱图
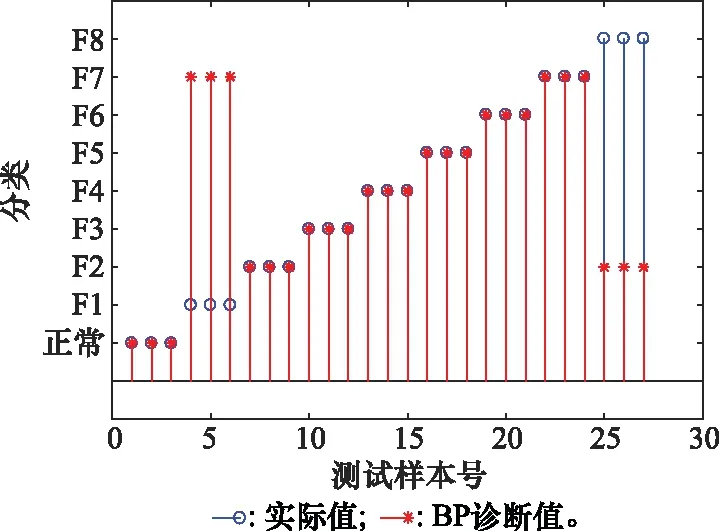
图15 实验2的BP诊断结果
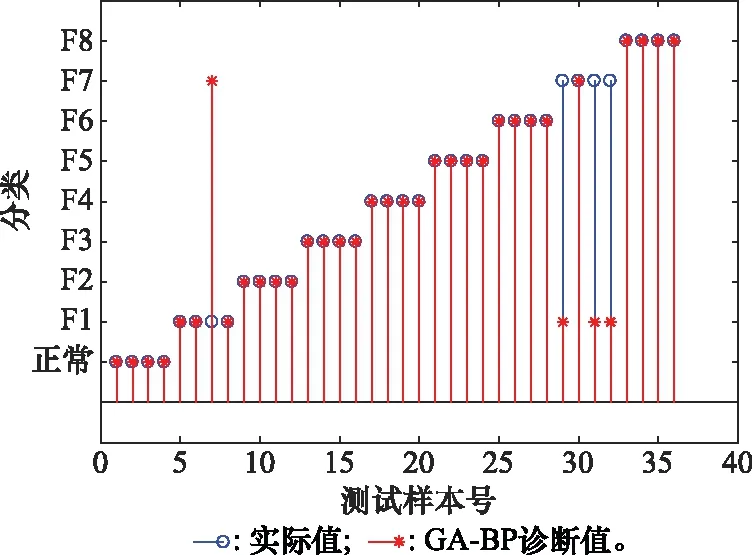
图16 实验2的GA-BP诊断结果
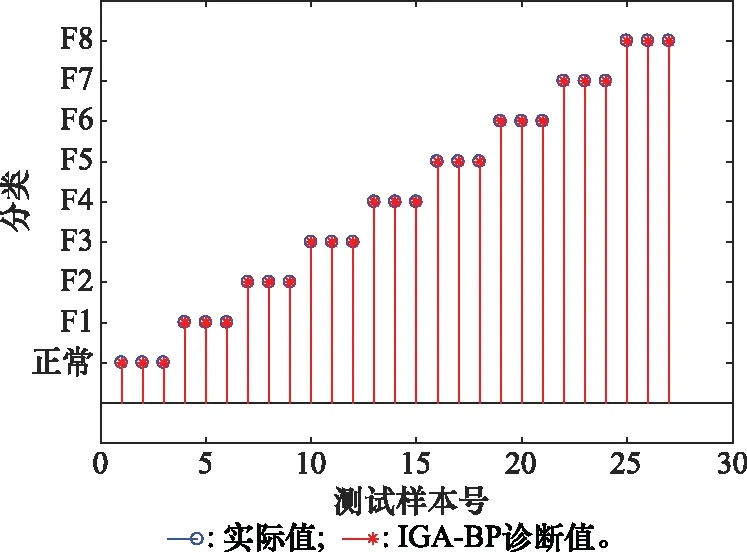
图17 实验2的IAG-BP诊断结果
最后,选择BP神经网络以及GA-BP神经网络,与本文所提IGA-BP神经网络进行对比实验。为了使其具有可对比性,采用相同的故障特征向量、相同的故障标记以及相同的训练集和测试集,得到的结果如表4所示。

表4 实验2故障诊断结果对比
本实验表明,所提算法可有效提取频率轴状态下获取的原始故障数据的特征向量,并且在面对较大模拟电路时,依然有效。
综合上述两个实验来看,不论输出对应的是时间轴还是频率轴,小波包分析均能有效提取特征向量。对于算法而言,由于BP神经网络样本需求量大,存在收敛速度慢,特别容易陷入局部极小值,故其诊断效果并不理想;而GA对其进行优化后,诊断效果有了大幅提升,但是依然存在一定误差,且由于GA存在盲目性和全局性,所以测试时间较长;再引入IA后,算法训练时产生的记忆单元可以在测试时快速反应,加快测试速度和收敛速度,且免疫单元具有靶向性,消除了GA的盲目性,从而提高了故障诊断的准确度。
4 结束语
本文提出了利用IGA优化的BP 神经网络诊断方法来实现模拟电路故障诊断。首先,通过小波包分析法对模拟电路故障输出响应信号进行分解,计算各频段能量,进行归一化处理形成故障特征向量。然后,利用IGA代替传统BP神经网络中采用的梯度下降法来优化BP 神经网络的参数选择过程。最后,将特征向量输入到优化后BP 神经网络模型中,实现对不同故障元件参数变化的分类诊断。实验结果表明,用上述方法优化后的BP神经网络模型相比传统模型能够大幅提高模拟电路故障诊断准确率。为模拟电路故障诊断提供了一种新方法,具有广泛的应用前景。

