基于GSPN的导弹多层级测试性需求建模与指标评估
翟禹尧, 史贤俊, 吕佳朋, 韩 露
(海军航空大学岸防兵学院, 山东 烟台 264001)
0 引 言
测试性需求(testability requirement, TR)也称测试性要求,包括定性要求和定量要求,除了说明测试性设计要“做什么”之外,也还要明确“做到什么程度”。测试性指标确定是测试性[1]需求分析亟待解决的重要问题,同时也是测试性建模[2]的前提。测试性指标越高,设备的先进程度以及技术手段的要求也会越高,变相提高了装备的设计、生产等方面要求[3]。
传统上采用参数修正法确定装备指标[4]。首先给出一些设计方案指标的初步估算,根据指标变化进行调整,直到满足给定精度。文献[5]对维修性指标进行论证,其结论可以作为测试性指标分析的基础。文献[6]将遗传算法引入系统级测试性指标确定中,该算法并未将系统性能与测试性相关联,更倾向于解的优化。文献[7]基于广义随机Petri网(generalized stochastic Petri net, GSPN)模型对导弹进行测试性建模,并求解测试性指标,虽取得良好的效果,但并未明确系统与子系统之间的参数如何关联,在实际应用中难以扩展。目前,主要通过类比法、经验法和权衡法[2]来确定测试性指标。传统方法虽能够获得装备的测试性指标[8],但它们是一种基于系统结构划分的、静态的求解方法,忽略系统层级间的维修保障等动态过程,所得结果并不准确。如何利用完备的测试性需求信息构建相应的体系,将这些信息作为约束条件解决测试性指标问题,是目前亟待解决的问题。
为了解决上述问题,本文提出采用GSPN进行测试性需求建模。GSPN是随机Petri网(srochastic Petri net,SPN)的进一步扩展,在SPN中引入瞬时变迁,求解相对容易[9-12]。采用GSPN进行测试性需求建模具有两大优势:① 模型优势:符合直觉的图形表示,既能描述系统的状态,又能表现系统行为。利用令牌的流动模拟系统的动态行为,适用于处理含有并发、冲突等逻辑关系的系统。因此,GSPN可以描述故障的发生、检测以及维修等一系列过程。② 信息利用优势:GSPN可以完美融入测试性需求信息,例如:故障事件发生与否可用可靠度来进行判断;模型中的延时变迁可表示维修保障过程,变迁使能参数可以定义为维修保障时间,此外变迁还可以定义为任务时间、故障隔离时间、故障检测时间以及概率参数,包括故障检测率和故障隔离率等;系统的可用度则可对应相应库所标识的稳态概率。多种信息融入模型,使得模型更加完备,得到的测试性指标也更加精确。
1 基于GSPN的导弹多层级测试性需求建模与分析
1.1 GSPN建模元素的图形化表示
GSPN可由8种元组描述[13-16],记为GSPN=(P,T;F,I,O,H,M0,λ),其中:
(1)P={P1,P2,…,Pn}为系统状态的集合;
(2)T={T1,T2,…,Tm}为有限变迁集合;
(3)F为连接库所、变迁的有向流;
(4)I,P×T为输入弧集合,×为笛卡尔积;
(5)O,T×P为输出弧集合;
(6)H表示禁止弧;
(7)M0为初始标识;
(8)λ={λ1,λ2,…,λm}为变迁的平均实施速率的集合。
结合测试性需求信息等因素,本文对GSPN模型[17-20]中的元素和符号的含义重新定义,如表1所示。

表1 模型中元素的含义
1.2 GSPN在不同领域中的应用
求解对象不同,GSPN解决问题的方式也是不一样的:① 在故障诊断中,主要根据输入输出相关矩阵,定义点火规则,采用诊断推理算法对其进行演绎推理确定故障源。② 在测试性建模中,利用令牌在库所中的流动性,每个库所表示一种故障模式,采用可达性算法得到故障相关性矩阵,进而完成测试性指标分析。③ 在测试性需求建模中,由于GSPN模型与嵌入马尔可夫链(embedded Markov chain,EMC)同构,可以采用同构法对其进行求解。利用该方式可以求解系统的稳态可用度,进而分析求解测试性指标,因此本文选用GSPN对系统进行测试性需求建模。
1.3 导弹系统结构
图1为导弹内部结构,图中包含7个子系统,任何子系统发生故障都会导致导弹系统不能正常工作。多数子系统不具有机内测试(built in test, BIT)功能,需要通过弹上计算机进行综合处理。在图2中,导弹划分为系统层、现场可更换单元(line replaceable unit, LRU)、车间可更换单元(shop replaceable unit, SRU)以及元器件等4个层级。

图1 导弹基本结构图

图2 导弹结构层次划分
层级不同对应着不同的维修级别,其维修方案亦不相同[21-23],例如系统层与基层级对应,LRU和SRU与中继级或基地级相对应。考虑文章篇幅,本文对导弹的系统层和LRU层进行建模分析,对应的维修级别为基层级和基地级。值得注意的是,如果有下一层测试性指标需求,可以将LRU作为研究对象向下进行分层建模,其建模过程和求解方式与本文论述一致。
1.4 问题建模

首先根据导弹基本结构图建立其故障维修的GSPN模型,如图3所示。图3中虚线框为子系统活动的简化过程,用变迁tF、tR表示LRU的故障和维修的速率或概率。
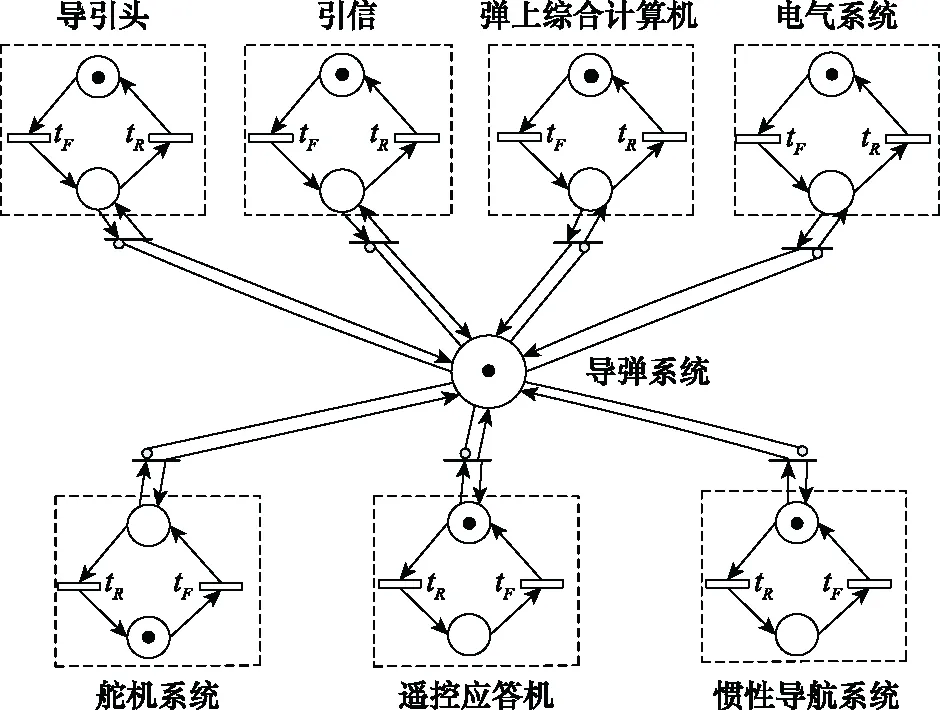
图3 宏观导弹系统的GSPN
细化图3的虚线框,建立系统两级测试性需求GSPN模型如图4所示,将导弹故障的发生、检测以及LRU的一系列活动关联起来。表2给出库所和变迁的具体含义,以及变迁的速率或概率值。

图4 系统两级测试性需求GSPN模型

表2 元素的具体含义1)
1.5 模型求解
GSPN模型与EMC同构,采用同构法对相应的EMC进行求解,可得到GSPN模型的稳定状态解[24-27]。设GSPN的状态空间为S,该空间包括实存状态集(时间变迁集)和消失状态集(瞬时变迁)两部分,这里采用T和V表示。
GSPN相应的转移矩阵可化[7,28]为
(1)
式中,矩阵A由XVV和XVT组成,XVV为消失状态向消失状态的转移率,XVT为消失状态向实存状态的转移率;矩阵B由XTV和XTT组成,XTV为实存状态向消失状态的转移率,XTT为实存状态向实存状态的转移率。
系统实存状态的转移矩阵为
U′=XTT+XTV(I-XVV)-1XVT
(2)
约化EMC(reduced EMC, REMC)的状态转移矩阵Q由U′得到,矩阵Q中的元素Qij为
(3)
设π为系统实存状态概率,则其满足
(4)
统稳态概率解可根据式(4)得到。
1.6 模型分解与简化
上述导弹的GSPN模型具有庞大的可达状态,不适合直接求解,需对模型进行简化,文献[28-29]介绍了一些常用简化方式。由于建立层次GSPN需求模型,因此可选择层次模型技术进行简化求解,将分系统表达的过程通过非基本变迁表示。


图5 LRU级测试与维修过程的GSPN简化为非基本变迁
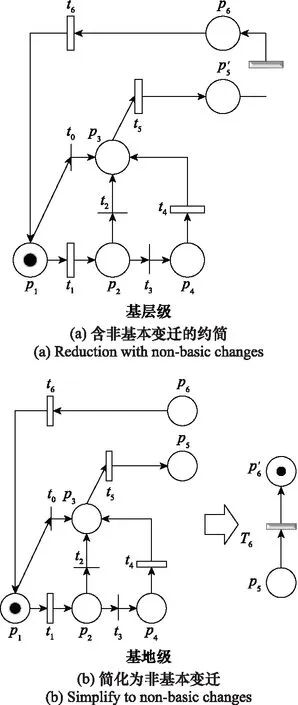
图6 系统级测试与维修过程的GSPN简化为非基本变迁
1.7 等效延时变迁的计算
等效变迁计算方法如下:
(1)在图7中,k个延时变迁ti(1≤i≤k)通过串联方式连接,其平均实施速率λi,它的等效非基本变迁T的λ可由下式给出:

图7 串联延时变迁的等效
(5)


图8 自由选择变迁的等效延时
(6)
1.8 系统GSPN模型分析与测试性指标确定
1.8.1 性能分析
(1)稳态概率分析
(2)化简后的系统性能分析

图9 非基本变迁简化的系统基本网
基本网SL两个状态库所的稳态概率分别表示为
(7)
(8)
且
(9)

(10)

1.8.2 测试性指标确定
稳态概率方程由多个变量构成,很难直接计算,当出现无解或者多个解时无法继续进行分析。可以根据系统要求采用控制变量法对稳态概率方程进行定性分析,再结合分析结果进行定量求解,完善测试性指标求解的具体过程,具体步骤如下:

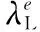

步骤 4通过与实际系统层测试性指标的对比,校验各LRU的测试性指标,其表达式为
(11)

2 案例分析与验证
以图4为分析对象,对系统的测试性指标进行确定。由于基地级指标求解基于基层级,因此基层级不受LRU个数的限制,求解时以两个LRU为例,并假设其故障检测与维修的时间相等,方便求解过程的细化分析。最后,通过仿真给出导弹7个LRU的实际指标。已知参数约束指标如表3所示,导弹稳态可用度要求不低于0.92,并规定所求测试性指标至少应满足系统级故障检测率0.91,故障隔离率为0.90。

表3 已知装备参数约束指标
2.1 各层级测试性要求分析
2.1.1 基层级测试性要求分析
首先根据第1.4节中的求解方法,求解基层级的稳态概率。导弹系统的可达标识(状态空间)如表4所示,其得到模型的可达标识{M0,M1,…,M5}。其中{M0,M2,M3,M4,M5}为实存态集,{M1}为消失状态集合。图10为图5(a)的各个状态转移过程。

表4 基层级可达标识

图10 状态可达图
根据第1.3节的GSPN求解过程,求得状态转移矩阵为
(12)
根据式(4)求得M0的稳态概率P(M0):
(13)
同理可求得P(M4):
P(M4)=(γFA+λ)·

(14)
式(13)和式(14)中各参数含义参考表2。


图11 稳态可用度与测试性指标关系曲线
综合上述分析可确定以下参数:
(1)平均人工测试时间不大于6.67 h;
(2)导弹系统的虚警率为γFA=0.9%;
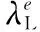
(4)基层级γFD≥0.92,满足系统要求。
2.1.2 系统基本网分析
2.1.3 基地级测试性要求分析

(15)
首先以两个LRU为例,对求解过程详细说明。LRU级ηi、μi相同,用ηL、μL表示,系统的LRU子网可化简为图12所示。

图12 系统两个LRU的简化图
(16)
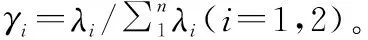
(17)
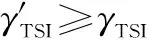
同时,γFD1和γFD2需满足系统层故障检测率约束,即
(18)

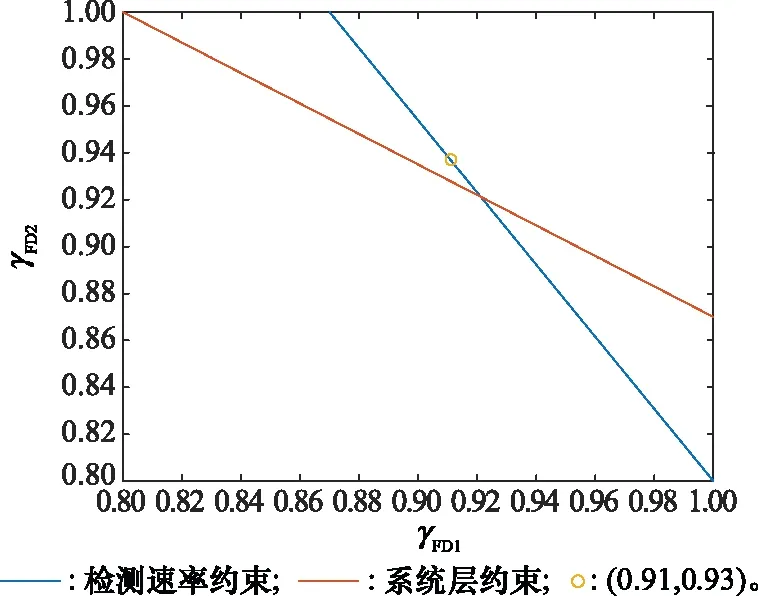
图14 γFD1、γFD2的取值域
本例重点分析和求解了系统层的γFD、γFA、1/λt以及LRU层的平均故障检测时间tFDL、γFD1和γFD2等测试性指标要求。综合上述分析,导弹系统与两个LRU所得具体测试性指标要求如表5所示。

表5 测试性指标要求
2.2 与传统测试性指标的故障率分配法比较
为验证实例分析所得到的γFDi的准确性,采用基于故障率的测试性指标分配法[17]进行对比分析。将获得的系统层γFD分配到两个LRU中。
首先计算各个LRU分配值:
(19)

(20)

上述对比分析反映出本文提出的测试性指标要求稍高于传统分配结果,原因是本文综合考虑故障检测、维修保障、可用度以及虚警等众多因素,对精度要求更高一些。
2.3 仿真验证分析
采用Stochastic Petri Net Packge(SPNP)对模型进行计算,通过可用度的误差来评估本文所提模型和算法的有效性。
(21)
误差不超过0.7%,验证了本文所提模型和算法的准确性。
2.4 导弹系统测试性指标确定分析
导弹系统的稳态可用度要求值为0.92,故障率为34(10-4/h),分系统实际数据如表6所示。导弹系统LRU的简化图如图6所示。

表6 导弹各LRU约束指标

图15 导弹系统LRU的简化图

(22)

(23)
同时,γFDi需满足系统层故障检测率约束,即
(24)
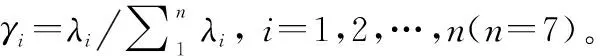
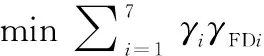

表7 导弹测试性指标

表8 导弹分系统测试性指标
3 结 论
现有方法不能全面考虑系统各项需求,无法保证测试需求分析的合理性和正确性。本文采用GSPN建立导弹多层次测试性需求模型,具体结论如下:
(1)简要介绍了GSPN的基本概念及含义,并给出导弹系统结构框图。基于上述准备工作,完成导弹测试性需求模型的建立。
(2)从数学角度将GSPN与EMC同构,采用同构法求解。GSPN具有庞大的可达状态,难以求解,根据层次模型技术对多层级GSPN模型进行简化,首先将分系统表达的过程通过非基本变迁表示,然后将整个系统进行简化,进而完成模型的求解。
(3)通过求解GSPN稳态概率,并采用定性分析与定量计算相结合的方法,分析和确定了导弹测试性指标要求,通过与传统测试性指标分配方法对比,验证了模型的有效性。采用SPNP软件进行仿真计算,可用度误差不超过0.7%,验证本文方法计算结果的准确性。
(4)本文综合考虑导弹多层级之间的维修保障以及测试性需求关联关系,更能反映导弹各层级测试性需求和指标要求,为导弹的指标确定提出一种更加科学合理的思路和方法,这对某些型号导弹的测试性工作具有实际意义。

