基于负熵最大化的压缩感知信道估计算法
赵迎新, 王长峰, 吴 虹,*, 张 铭, 黄英杰, 王乐耕, 刘之洋
(1.南开大学电子信息与光学工程学院, 天津 300350;2.天津市光电传感器与传感网络技术重点实验室, 天津 300350)
0 引 言
随着大规模机器通信与物联网技术的发展,通信技术向着“全覆盖、全频谱、全应用”的方向发展,未来通信网络架构将向着蜂窝移动通信和卫星通信结合的方向发展,这就不可避免地增大无线通信频谱使用范围,使得信道的稀疏性变得尤其明显[1-2]。压缩感知技术可以对存在稀疏性的信号进行采样编码,并且利用信号重构算法恢复原始稀疏信号。有研究[3]表明,可以利用压缩感知技术对存在稀疏表现的信道进行估计,获取信道状态信息。利用压缩感知的传统信道估计算法,主要分为贪婪算法,凸优化类算法以及组合优化算法3类。以匹配追踪(matching pursuit, MP)算法、正交MP(orthogonal MP, OMP)算法为代表的贪婪类算法进行信道估计时,需要提前了解稀疏信道的稀疏度等先验信息,往往难以直接获取[4]。而以基追踪(basic pursuit, BP)算法、最小绝对值收敛和选择(least absolute shrinkage and selection operation, LASSO)算法为代表的凸优化类算法对信道中的非高斯噪声难以适应,对复杂噪声缺乏足够的鲁棒性[5-6]。针对这种情况,国内外学者提出了若干种LASSO改进算法,其中包括加权l1范数LASSO算法[7]等。选取加权l1范数LASSO算法作为本文提出算法的对照算法之一,加权l1范数LASSO算法在传统的LASSO算法基础上,通过循环迭代优化l1范数前的权重w,从而达到更高的迭代速度与精度。组合优化算法虽然对于信道状态信息的求解精度高,但是对于观测向量的需求量极大,并且求解迭代收敛速度缓慢。
本文针对凸优化类算法面对信道复杂噪声时鲁棒性差的问题,通过利用负熵最大化算法替代误差函数最小化的同时,将稀疏约束优化为更为精确的lp范数,提出了一种新的基于LASSO的改进算法。
1 传统基于压缩感知的信道估计方法
随着海量机器通信的发展,无线通信传输带宽大大变宽,此时信道表现出明显的稀疏特性。能充分利用稀疏性的压缩感知技术被引入到信道估计领域中。压缩感知是一种新的信号采样原理,该理论指出只要信号在某一变换域中是稀疏的,就可以通过构造观测矩阵将该稀疏信号映射到低维空间,进而通过求解优化问题还原出原稀疏信号[8]。根据压缩感知的理论描述,对于稀疏信号的压缩采样过程可以描述为
y=Φs
(1)
式中,Φ是大小为M×N的观测矩阵,作用是对信号进行降维;s是N×1的稀疏向量,稀疏度为K。在δk∈(0,1)的条件下,观测矩阵需要满足[9]有限等距(restricted isometry propetry, RIP)准则:
(2)
压缩感知算法的目的是利用观测向量y与观测矩阵Φ还原出稀疏信号。利用原信号的稀疏性,可以将压缩感知的求解问题模型表示为
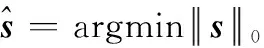
s.t.y=Φs
(3)
该问题是一个非线性问题,求解过程复杂,针对这个问题,学者提出了一系列算法来求解,其中以凸优化算法中的LASSO算法[10]最具代表性,在LASSO算法中,使用l1范数来替代l0范数,将求解模型转化为
s.t.y=Φs
(4)
将稀疏约束作为惩罚项:
(5)
式中,非负数λ为正则化参数,用于权衡约束项与误差项。
随着无线通信传输带宽的增加,信道响应呈现出明显的稀疏性,以正交频分单用(orthogonal frequency division multiplexing, OFDM)系统为例,当相干时间大于一个符号周期时,信道响应可以被稀疏表示为
(6)
式中,ηi表示多径中第i条路径的衰减系数;τi表示多径中第i条路径的时延;k表示多径的数量。大多数多径信道能量较小,可以认为多径系数为零,只有几个能量较大的多径且相隔较远。设信源发送信号为X′=[x0,x1,x2,…,xN-1],经过无线多径信道可得到频域信宿接收的信号,压缩感知信道估计模型为
Y=XH+N=X(Wh)+N
(7)
式中,X=diag(x0,x1,x2,…,xN-1);Y=[y0,y1,y2,…,yN-1]T;W为快速傅立叶变换(fast Fourier transform, FFT)矩阵;N为信道加性噪声干扰。导频处的接收信号为
Yp=(XpWp)h+Np
(8)
由于信道噪声Np在频域不具有稀疏性,故在利用压缩感知中的LASSO算法的过程中可自然忽略。类比压缩感知模型y=Φs,即可重构出稀疏信道响应h(τ):
(9)
2 基于负熵最大化并结合lp正则化的压缩感知信道估计算法
随着研究发现,只有当信道干扰噪声为高斯型噪声时,上述压缩感知信道估计算法通常才具有比较优越的性能。但是在后5G时代,随着地面网络与天基卫星网络的结合,引入的雨衰与频率峰值吸收现象,给无线信道带来了大量的脉冲噪声[11]。针对这些情况,传统的LASSO算法并不能高性能地恢复出信道信息。为了提高信道估计的精确度,本文依据信息论中的最大负熵理论和稀疏编码策略,从以下两个方面提出新型压缩感知信道估计思路与方案。
2.1 稀疏约束:lp正则化
信道估计中的压缩感知算法为了保证重构出的信道信息具有稀疏性,通常在基本模型中加入正则化条件进行稀疏约束,传统的LASSO算法使用l1范数进行稀疏约束。从赋范空间的角度考虑,图1是二维向量在lp(0≤p≤1)范数下定义的单位球。

图1 lp(0≤p≤1)范数下定义的单位球
虽然用l1范数替代l0范数能够使问题简化,但不可避免地引入稀疏性精确度的误差,但是如果使用lp(0≤p≤1)范数却能够极大程度地减小该误差。因此本文将引入lp(0≤p≤1)范数作为问题的稀疏约束,并比较其与传统的利用l1范数作为稀疏约束的LASSO算法的性能差异。
lp(0≤p≤1)范数的数学表达式为
(10)
研究[12]表明,当0.5≤p≤1,p值越小,稀疏性表达准确度越高,但是当0≤p≤0.5时,p值的减小却没有明显带来稀疏性表达准确度的提高,反而极大地提高了计算的复杂度,故本文采用l0.5范数作为稀疏约束进行压缩感知信道估计。
在传统利用l1范数作为稀疏约束的LASSO信道估计算法[13-14]中,通过定义一个替代函数g(h,hk-1)估计信道状态信息:
(11)
通过求解函数g(h,hk-1)的极值即可达到求得函数f(h)的极值的目的,估算出稀疏信道的状态信息。
通过对式(11)的化简可得
(12)
可以发现这是一个经典的软阈值函数求解极值问题,根据软阈值函数求解极小值的模型[15-16],由式(12)可以求解出稀疏向量的每一个元素,即得到式(12)的最优解:
(13)
式中,βk-1=hk-1+η(XpWp)T[Yp-(XpWp)hk-1]。
同理,采用lp(0≤p≤1)范数作为稀疏约束时,求解稀疏信道向量h可以表示为
(14)
根据LASSO算法的求解过程可以将其转化为
(15)
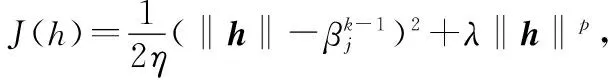
(16)
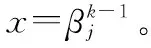
当p=0.5时有
可得
hopt=
(17)
2.2 误差函数:负熵最大化
根据香农信息论,在所有等方差的随机变量中,高斯变量的熵值最大,即可以用熵值来衡量变量的高斯性。由此可得负熵值是衡量变量的非高斯性的一个重要指标,负熵越大,变量的非高斯性就越强。
为了提高传统的LASSO算法对于复杂信道噪声的鲁棒性,增强其对信道非高斯型噪声的适应,本文提出以负熵为误差函数的建模思路。算法在迭代运算过程中,通过最大化误差函数的负熵使得其高斯性得到增强,并且可以容忍小的分量误差的存在,以此换来在显著非零分量上的高精度,提高模型对误差的容错能力。通过最大化误差函数的负熵使得算法能够更好地适应信道脉冲噪声等复杂噪声的干扰,从而更加有效而精确地进行稀疏信道重建。
负熵的定义式为
N(e)=H(eGuass)-H(e)
(18)
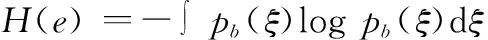
N(e)={E[G(e)]-E[G(eGuass)]}2
(19)
式中,E(·)表示数学期望;G(·)表示非线性函数运算,常用的非线性函数有tanh(c·e),e3log(cosh(c·e))等,c为仿真选用的随机参数。
根据最大负熵理论,可以将压缩感知信道估计模型式(8)表示为
(20)
根据最大负熵理论可知E[G(e)]≤E[G(eGuass)],故式(20)等价于
(21)
针对式(21)的求解,本文通过多次迭代求取局部最小解使得目标函数收敛于全局最小值。首先,令函数在初始向量h0对其进行一阶泰勒展开:
(22)
通过求取h0邻域函数的极小值点hk,将其作为下一次迭代的起始点。通过多次迭代,使得局部最小值点收敛于全局最小值点,即可求出信道状态信息。其数学模型可表示为
(23)
为求解式(23),根据文献[18]提出的近似点算法,构造一个替代函数J(h,hk-1)取代目标函数f(h):
(24)
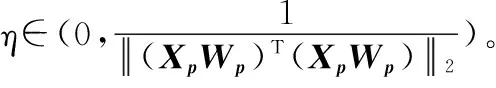
(25)

采用G(e)=log(cosh(c·e))作为负熵中的非线性函数,可求得迭代结果为
(26)
加入稀疏约束l0.5范数,式(26)进一步表达为
(27)
令βk-1=hk-1-η(XpWp)Ttanh[c(XpWp)hk-1-Yp],由l0.5正则化的计算过程及软阈值函数的求解模型可知,求得的稀疏信道响应为
(28)
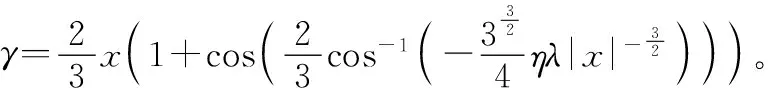
综上所述,本文提出的信道估计算法模型由lp正则化稀疏约束以及误差函数的负熵最大化两部分构成。算法的求解过程通过在目标函数的初始点上进行一阶泰勒展开,进而利用近似点算法对目标函数进行添加配方项,将其转化成标准二次函数的形式,最后利用lp正则化稀疏约束,通过利用软阈值函数求解模型,多次迭代使得目标函数收敛于全局最小值点,即可估计出信道状态信息。算法1具体步骤如下。

算法1 基于负熵最大化与lp正则化的稀疏信道估计算法输入 接收信号导频处信息Yp,发送信号导频处信息Xp,FFT矩阵Wp输出 稀疏信道状态信息h初始化η∈(0,1‖(XpWp)T(XpWp)‖2),λ>0,h0∈RN,k=1循环执行步骤1~步骤3步骤1 βk-1=hk-1-η(XpWp)Ttanh[c(XpWp)hk-1-Yp]步骤2 hki=γsign(max(0,|βk-1i|-32λη23))步骤3 k=k+1当误差函数收敛于全局最优解时停止循环迭代
3 系统仿真与性能比较
为了验证基于负熵最大化和lp正则化的压缩感知信道估计算法的有效性,本文搭建了一个OFDM无线传输系统,在发送端采用插入导频的方式,估计不同噪声类型干扰下的信道信息,并与传统的最小均方(least square, LS)信道估计算法,LASSO 压缩感知算法以及加权l1范数LASSO算法进行对比,分析不同算法的信道估计性能。信道模型为瑞利信道,信道干扰噪声分别为加性高斯噪声和脉冲噪声。系统参数如表1所示,算法参数如表2所示。

表1 OFDM系统参数设置

表2 算法参数设置
在系统信噪比(signal to noise ratio, SNR)为16 dB的情况下,不同算法估计的信道冲击响应与真实信道冲击响应的对比图如图2和图3所示。其中,图2和图3分别为信道干扰噪声为高斯型噪声与非高斯型噪声的情况,Error表示估计信道冲击响应与真实信道响应的相对误差值。从图2和图3可以看出,LS算法,LASSO算法、加权l1范数LASSO算法以及基于负熵最大化及lp正则化的压缩感知信道估计算法虽然均基本估计出了稀疏信道响应的位置,但是LS算法却未能较好地体现出信道的稀疏性,在真实信道响应为0的位置存在一个微小的数值,LASSO在非零位置的信道估计幅度精度存在较大误差,加权l1范数LASSO算法能较准确地估计出状态信息,但与本文提出的算法相比,无论在估计稀疏信道位置或信道响应幅度上,基于负熵最大化及lp正则化的压缩感知信道估计算法均展现出更优良的性能。
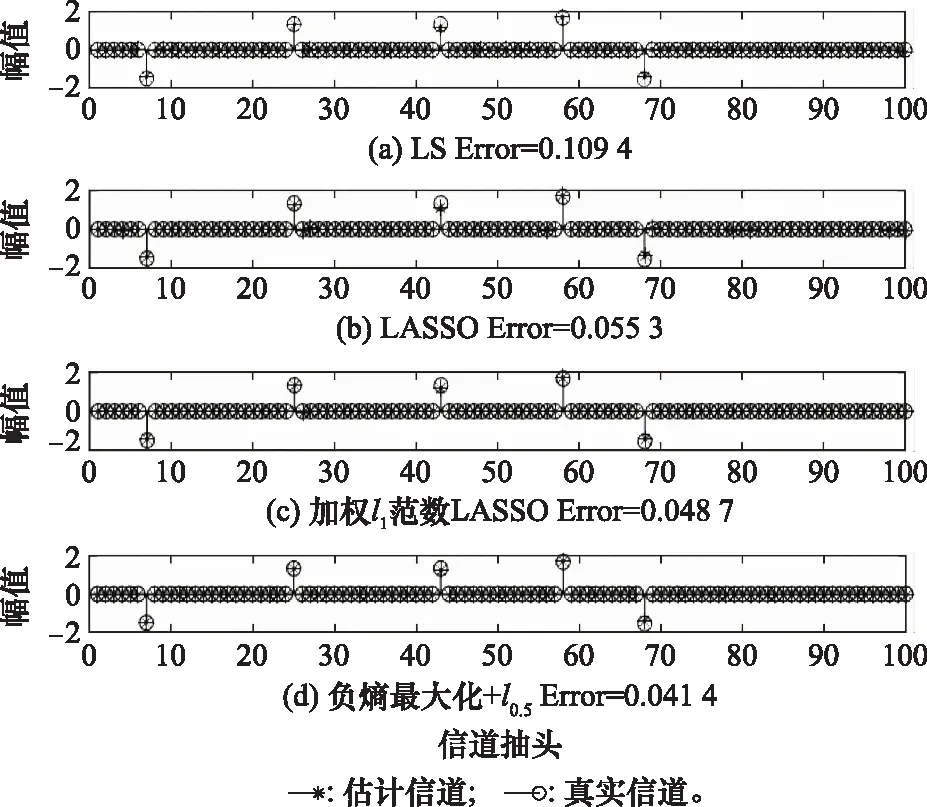
图2 高斯噪声下估计信道与真实信道对比
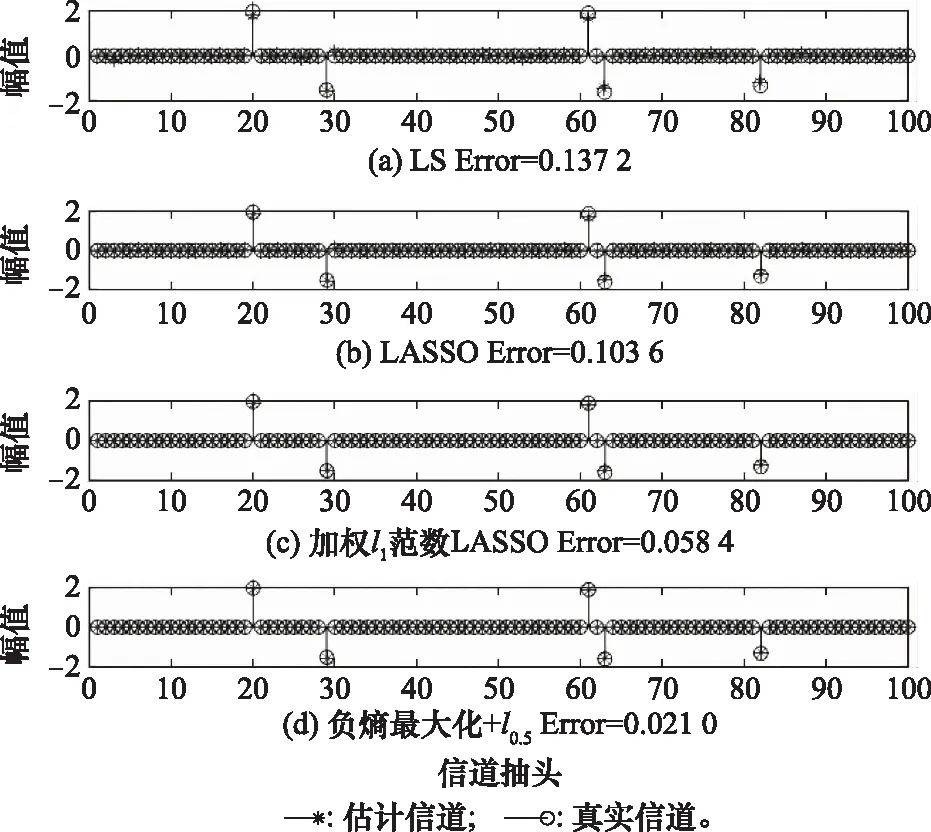
图3 脉冲噪声下估计信道与真实信道对比
在高斯噪声干扰下,LASSO算法、加权l1范数LASSO算法和基于负熵最大化及lp正则化的压缩感知信道估计算法的精度相差不大,然而在脉冲噪声干扰的情况下,LASSO算法信道估计的精度明显下降,加权l1范数LASSO算法信道状态估计表现不佳,显示出其在复杂噪声条件下的鲁棒性较差。本文提出的算法在脉冲噪声条件下表现出明显的优势,信道估计相对误差值低,表现了该算法对于非高斯型噪声良好的适应性。
本文搭建的系统在发送端的子载波中等间隔地插入13个导频,利用LS算法、LASSO算法、加权l1范数LASSO算法和基于负熵最大化及lp正则化的压缩感知信道估计算法进行信道估计。图4和图5为信道干扰噪声为高斯噪声情况下,在上述两种情况下,不同算法的信道估计均方误差(mean square error, MSE)和信号传输误比特率(bit error rate, BER)情况。

图4 高斯噪声情况下信道估计MSE随SNR的变化曲线
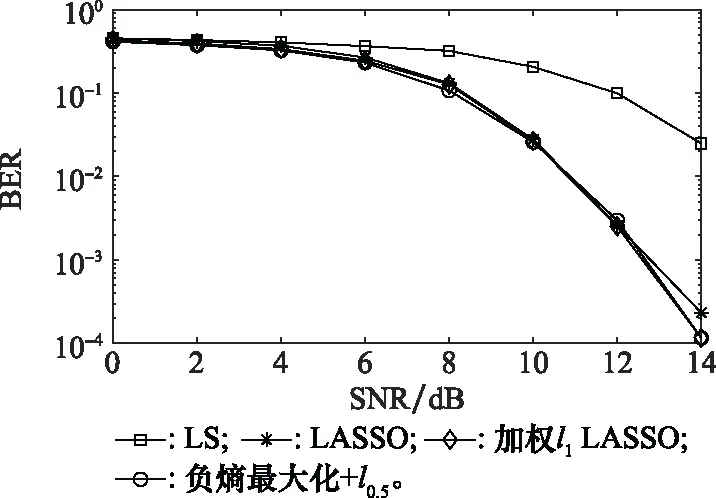
图5 高斯噪声情况下信息传输BER随SNR的变化曲线
从图4和图5可以看出,总体来说当信道干扰噪声为高斯型噪声时,LASSO算法、加权l1范数LASSO算法与基于负熵最大化及lp正则化的压缩感知信道估计算法对于信道状态信息的估计性能相差不大,但是在低SNR的情况下,基于负熵最大化及lp正则化的压缩感知信道估计算法有着更好的信道估计性能。
图6和图7是信道干扰噪声为非高斯型脉冲噪声情况下,不同算法信道估计MSE和信号传输BER情况。为了突出说明基于负熵最大化及lp正则化的压缩感知信道估计算法在信道噪声为非高斯噪声时的性能优势,在原有仿真基础上额外加入在发送端的72个子载波之间等间隔的插入25个导频,利用LS算法进行信道状态信息估计的仿真对照。从图6和图7可以看出,当信道干扰噪声为脉冲噪声时,此时基于负熵最大化及lp正则化的压缩感知信道估计算法表现出相比于LS算法、LASSO算法以及加权范数LASSO算法更明显的优势,体现为更低的信道估计MSE和信息传输BER,表现了更强的抗非高斯噪声的性能。基于负熵最大化及lp正则化的压缩感知信道估计算法使用13个导频达到了比LS算法使用25个导频更低的BER和信道估计MSE,充分体现了算法在提高信道估计性能的前提下,在降低导频开销,节省系统资源,提高频带利用率方面的优越性。
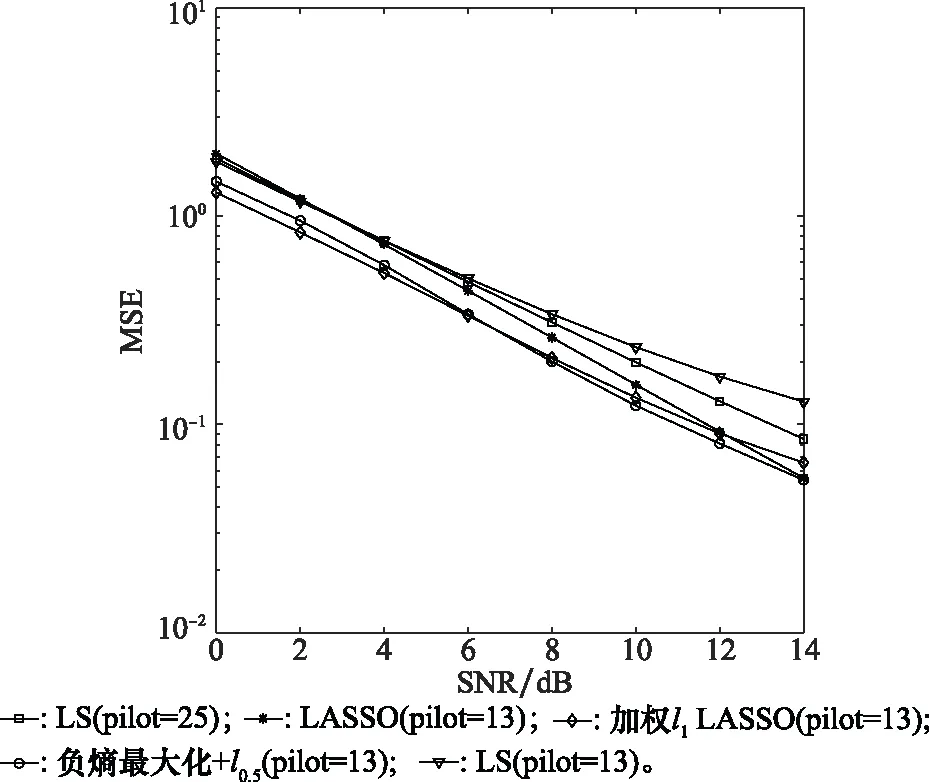
图6 脉冲噪声下信道估计MSE随SNR的变化曲线

图7 脉冲噪声下信号传输BER随SNR的变化曲线
图8为SNR为14dB,信道干扰噪声为脉冲噪声时,随着信道稀疏度的变化,不同算法进行信道估计时MSE的变化情况。
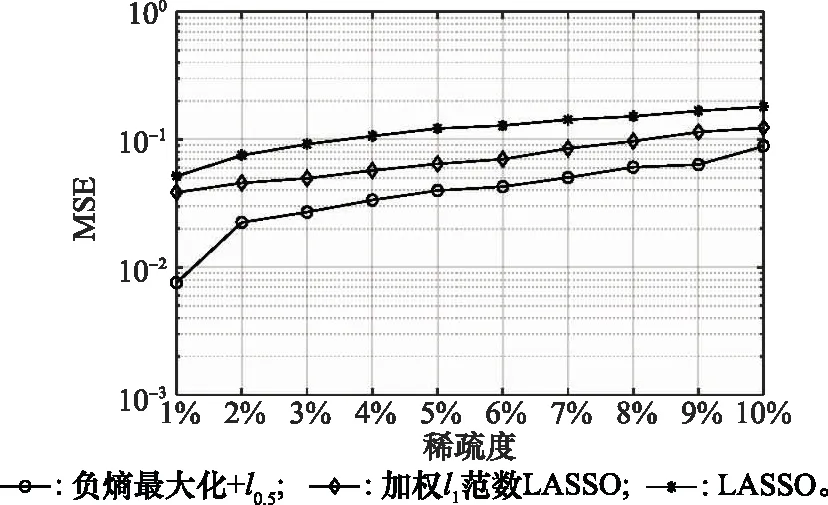
图8 信道估计MSE随信道稀疏度的变化曲线
随着信道稀疏度的增加,不同算法对于稀疏信道的估计效果均在变差,但是基于负熵最大化及lp正则化的压缩感知信道估计算法相较于其他算法均具有一定的优势,信道估计MSE仍然能够保持在10-2数量级内,反映出本文提出的算法对于信道稀疏度变化拥有良好的适应性。
通过采取比较传统LASSO算法、加权l1范数LASSO算法以及基于负熵最大化及lp正则化的压缩感知信道估计算法在同一平台上的运行时间,评估以上算法不同的算法复杂度对于通信系统整体性能的影响。仿真系统平均运行时间如表3和表4所示。

表3 高斯噪声情况下算法平均运行时间

表4 非高斯噪声情况下算法平均运行时间
表3和表4表明,不论信道噪声是高斯噪声还是非高斯噪声,基于负熵最大化及lp正则化的压缩感知信道估计算法相较于传统LASSO算法,算法系统平均运行时间并没有明显增长,却能够显著提升信道状态信息估计精度。同时相较于加权l1范数LASSO算法,基于负熵最大化及lp正则化的压缩感知信道估计算法不仅在信道估计系统平均运行时间上占据优势,同时信道状态信息的估计也更为准确。
4 结 论
本文提出一种基于负熵最大化并结合lp正则化的压缩感知信道估计算法,仿真表明该算法能够在不对通信系统造成明显影响的前提下,对于非高斯信道噪声条件下的信道估计具有更好的性能。同时该算法可以使用更少的导频达到比传统信道估计方法更好的效果,在适应复杂噪声干扰的同时,节约导频开销,提高频谱利用率,为后5G时代全覆盖、全频谱、全应用的无线通信所导致的稀疏信道估计提供了一个高效可行的技术方案。

