一种不依赖超参数的稀疏信号单快拍DOA估计方法
虞 飞, 余 赟, 周利辉, 彭春光
(中国人民解放军92578部队, 北京 100071)
0 引 言
信号波达方向(direction of arrival,DOA)估计是阵列信号处理中一项极为重要的研究分支,已在声纳、雷达、通信、导航、地震探测等领域取得广泛应用[1]。以MUSIC[2-3]和ESPRIT[4]算法为代表的传统子空间类DOA估计算法在高信噪比(signal to noise ratio, SNR)、非强相关源和多采样快拍数的情况下可获得超分辨估计性能。但在实际应用中,高SNR、非强相关源和多采样快拍数都是比较理想的环境因素,只要有一个因素不满足,这些算法的DOA估计精度将严重下降甚至估计失败。为此,学者们提出了很多改进算法,如适用于单快拍的阵列测向方法[5-7],适用于相干情形的空间平滑类算法[8-10]等。然而,这些改进算法都只适用于某一个非理想环境因素下的高性能估计,当同时存在至少两个非理想环境因素时,这类算法依然面临着失效问题。
近年来,基于稀疏表示框架的阵列参数估计方法由于在低SNR、有限采样快拍数据、相干信号、信号DOA角度间隔小等非理想条件下同时具有良好的估计性能而引起了相关学者的广泛关注,并取得了大量高质量的研究成果[11-15]。考虑到在实际应用中,通常目标信号个数远小于传感器阵元数,目标信号DOA相对于空间来说也是稀疏的,故可将传统的传感器阵列输出模型进行稀疏化表示,得到阵列输出数据的稀疏表示模型。于是,稀疏表示理论中的很多方法很自然地被引入到阵列信号处理问题中,而传统的阵列参数估计问题转化为稀疏参数求解问题。基于稀疏表示的阵列测向方法在非理想条件下整体性能优于传统的子空间类测向方法,但分析表明,前者的计算复杂度明显高于后者,导致算法对目标信号DOA估计的实时性变得很差。同时,这类方法在求最优解过程中,还面临着一个甚至多个超参数(或者正则化参数)选取的问题,超参数的选择是否合适直接关系到最终的稀疏恢复性能。因此,还需要对超参数进行精细选取,然而目前还没有明确的方法用来指导超参数的选择。
本文依托阵列输出数据的稀疏表示模型,提出了一种基于加权最小二乘(weighted least squares,WLS)准则的单快拍DOA稀疏迭代自适应估计(简称为WLS-IAE)算法。该算法不仅保持了稀疏表示框架在非理想条件下的良好估计性能,而且避免了传统稀疏参数求解方法的高复杂度和经验式的超参数选取问题,仅采用单快拍即获得高精度DOA估计,因此非常适用于快变目标信号DOA的实时跟踪测量,具有潜在的工程实用价值。
1 阵列输出模型
考虑K个远场窄带信号入射到由M个无方向性(全向)阵元构成的均匀线性阵列(uniform linear array,ULA)中,并假设K个信号与ULA在同一平面内(在实际应用场景中,如水下声纳基阵测向,我们经常只关心某一平面内信号的入射方位,或者入射信号在该平面内的投影,因此这一假设可以得到保证)[16]。将阵元由1到M进行编号,并以阵元1作为基准或参考阵元。设参考阵元处的任一接收信号变换到基带后有如下形式:
s(t)=a(t)ej[ω0t+φ(t)]
(1)
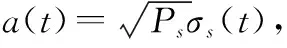
那么,在t时刻,整个阵列的M×1维输出数据模型为
x(t)=As(t)+n(t)
(2)
式中,s(t)=[s1(t),s2(t),…,sK(t)]T为变换到基带后的参考阵元处接收到的K个信号构成的列向量;n(t)=[n1(t),n2(t),…,nM(t)]T为阵列的零均值加性复高斯白噪声向量;A=[a(θ1),a(θ2),…,a(θK)]为M×K维导向矢量矩阵,且对于ULA,导向矢量a(θk)[17]可定义为
(3)
式中,d为相邻阵元间距;λ为信号波长;θk为第k个信号的DOA,通常定义为该信号入射方向与ULA法线方向的夹角,则有θk∈[-π/2,π/2]。
2 模型的稀疏表示与稀疏矩阵方程的求解
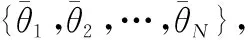
x(t)=Φγ(t)+n(t)
(4)
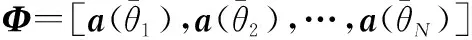

min‖γ(t)‖0s.t.‖x(t)-Φγ(t)‖2≤β
(5)
式中,l0-范数‖γ(t)‖0表示向量γ(t)中非零元素的个数;‖·‖2表示向量的2-范数;正则化参数β用来指定允许的噪声水平。
直接求解优化问题式(5),必须筛选出向量γ(t)中所有可能的非零元素,由于搜索空间过于庞大,故此方法是非确定性多项式时间(non-deterministic polynomial-time, NP)难题。
考虑到l1-范数是最接近于l0-范数的凸目标函数,目前,使用最广泛的求解方法是将式(5)的l0-范数最小化问题转化为凸松弛的l1-范数最小化问题(简称l1-min算法)[18],即
min‖γ(t)‖1s.t.‖x(t)-Φγ(t)‖2≤β
(6)
式中,‖·‖1表示向量的l1-范数。该式可以很容易转化为二阶锥规划(second-order cone programming,SOCP)问题的一般形式,从而在二阶锥规划的框架下求解。但在实际应用时,目标可能来向的角度范围θ在网格划分时其数量级将达到104,这将明显降低二阶锥规划问题的求解速度,导致算法对DOA估计的实时性变得很差。
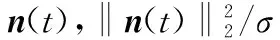
3 基于WLS的稀疏迭代自适应估计方法
假设稀疏信号矢量γ(t)与噪声矢量n(t)之间相互统计独立,则由式(4)可得
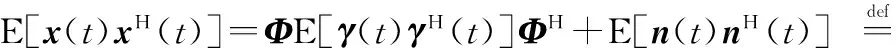
ΦPΦH+Rn
(7)
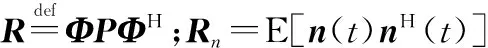
P=diag[p1,p2,…,pn,…,pN]
(8)
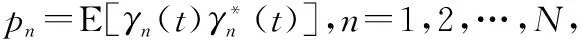
定义干扰(即稀疏信号矢量γ(t)中除了第n个信号γn(t)之外的其他所有信号)的协方差矩阵为
(9)

(10)
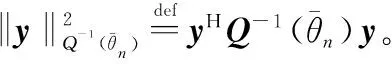
为求得式(10)的最优解,将该式展开并处理得如下形式:
(11)
式中,
故关于γn(t)的加权最小二乘估计为
(12)
将式(9)代入式(12),根据矩阵求逆引理可得
(13)
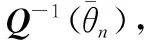
(14)
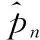
(15)
相应地有
(16)
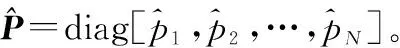
重复计算:
forn=1,2,…,N
end
直至收敛。
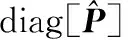
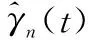
(17)

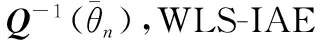
(18)
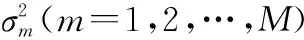
(19)
式中,向量em表示M×M维单位阵IM=[e1,e2,…,eM]的第m列。
综上,WLS-IAE算法最终形式归纳如下。
初始化:
重复计算:
forn=1,2,…,N
end
直至收敛。
4 算法计算量分析
l1-min算法和本文提出的WLS-IAE算法都是基于稀疏表示框架的单快拍DOA估计方法,其中,l1-min算法作为依赖于超参数的稀疏估计类方法具有一定代表性,在其基础上发展了很多改进算法。下面详细分析WLS-IAE算法的计算量,并与l1-min算法进行比较。
令MDN表示复数乘除法运算的次数。首先分析本文算法初始化的计算量,再分析算法迭代过程的计算量。
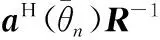
(20)
结合WLS-IAE算法初始化过程的计算量,则WLS-IAE算法实现所需的MDN总次数约为
(21)
l1-min算法一般是将式(6)的凸松弛的约束优化问题转化为二阶锥规划问题的一般形式,并在二阶锥规划的框架下采用内点法求解,其计算复杂度为O(N3)[18]。
考虑到在实际应用中,M≪N,nitr≈10,则nitr≪N,且一般有nitr≪M成立,则WLS-IAE算法的计算复杂度为O(M2N)。
因此,虽然同为基于稀疏表示框架的DOA估计算法,WLS-IAE算法的计算复杂度远低于l1-min算法,具有更好的实时性。
5 仿真实验
在以下仿真实验中,考虑由15个阵元构成的均匀线性传感器阵列,相邻两个阵元间距为信号波长的一半,即d=λ/2。假设两个单位功率的窄带信号分别从不同方向入射到上述传感器阵列,实验中取阵列对信号的单快拍采样数据。SNR定义为
下列实验中,如无特别说明,取SNR=10 dB。
(1)算法收敛特性
考虑两个相干信号DOA参数分别以θ1=-10°,θ2=60°入射到上述均匀线阵。图1给出了采用WLS-IAE算法分别在初始化、迭代1次、迭代5次、迭代10次过程中对DOA估计的归一化稀疏功率谱图。其中算法初始化采用的是CBF算法。两个相干信号之间的关系表示为s2(t)=s1(t)ςejη,其中,ςejη为相关系数,反映了两个信号之间的数值关系。实验中取ς=1,η=π/6。
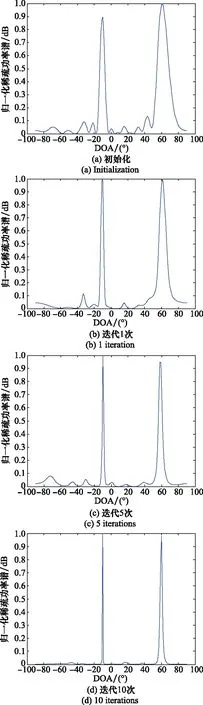
图1 WLS-IAE算法中DOA估计的归一化稀疏功率谱
从图1的4组仿真曲线可以看出,本文提出的WLS-IAE算法在相干信号的真实目标方向上形成了谱峰。随着迭代次数的逐渐增加,稀疏功率谱的谱峰变得越来越尖锐,而“伪峰”及旁瓣逐渐消失,意味着该算法在迭代10次时对目标信号DOA具有较高的估计精度和分辨率。在改变其他实验参数的情况下,算法一般不超过15次迭代即可达到收敛状态,说明本文算法具有较快的收敛速度。
(2)算法对相干信号DOA估计的分辨率
考虑两个相关系数为ejπ/6的邻近相干信号参数θ1=-10°,θ2=-6°入射到上述均匀线阵,采用CBF算法、WLA-IAE算法和l1-min算法对单快拍阵列接收数据分别进行10次蒙特卡罗仿真实验,得到3种算法对DOA估计的归一化稀疏功率谱图,分别对应如图2(a)~图2(c)所示。
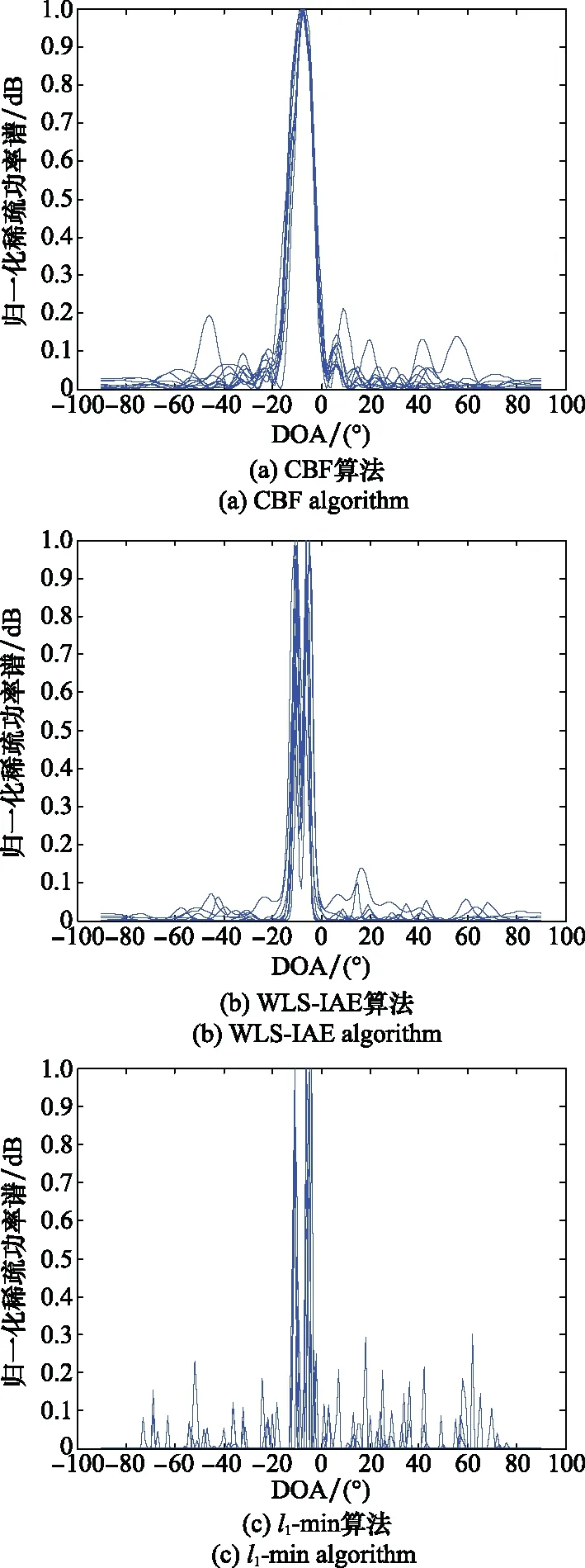
图2 角度间隔较小的两个相干信号DOA估计的归一化稀疏功率谱
由图2的仿真曲线可以看出,当相干目标信号的角度间隔较小时,采用WLS-IAE算法和l1-min算法均可以在真实的目标方向形成尖锐的谱峰,实现了对目标信号DOA的高分辨率估计。相反,CBF算法在两个真实目标方向上的谱峰合二为一,说明此时CBF算法无法分辨两个信号的DOA。综上表明,在单快拍情形下,基于稀疏表示的阵列测向方法对空间邻近信号仍具有较好的分辨能力。
(3)SNR对DOA估计精度的影响
考虑两个相关系数为ejπ/6的相干信号DOA参数分别以θ1=-10°,θ2=60°入射到上述均匀线阵,采用WLA-IAE算法、l1-min算法、CBF算法、快速迭代内插波束形成(fast iterative interpolated beamformer,FIIB)算法[5]和稀疏协方差矩阵迭代的单快拍(sparse covariance matrix iteration with a single snapshot,SCMISS)算法[15]分别进行200次蒙特卡罗仿真实验,得到目标信号DOA估计的均方根误差(root-mean-square error,RMSE)随SNR的关系曲线,如图3所示。其中,L次蒙特卡罗仿真实验得到的DOA估计的RMSE定义为
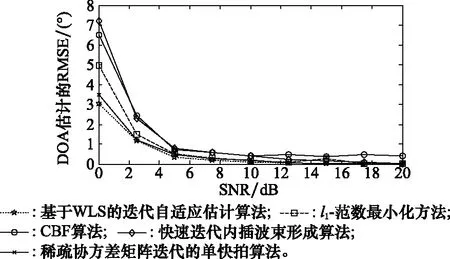
图3 DOA估计的RMSE随SNR的关系曲线
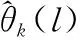
从图3的仿真曲线可以看出,随着SNR的逐渐提高,采用上述5种算法估计的DOA的RMSE都是逐渐减小的,说明5种算法对DOA的估计精度均越来越高。其中,WLA-IAE算法对DOA的估计精度最高,尤其在低SNR时估计精度优势更明显,表明WLA-IAE算法在相干信号、单快拍、低SNR等非理想情形下均具有很好的估计性能。
CBF算法的估计性能因受阵列孔径的限制,显然不如WLS-IAE、l1-min和SCMISS超分辨算法,它们都属于基于稀疏表示框架的阵列测向方法,在低SNR情况下都具有良好的估计性能。但是,l1-min算法的稀疏恢复性能依赖于正则化参数β的精细化选取,一旦选取不当,算法存在收敛至局部极值的风险。虽然本文在第3节给出了正则化参数β的选择依据,但正如文献[18]所述,这种选择依据只适用于高SNR情况下,在低SNR时对正则化参数β只能凭经验公式选取,而WLS-IAE算法属于一种不依赖超参数的稀疏估计类方法,因此WLS-IAE和l1-min算法在高SNR时性能相当,而在低SNR时前者性能优于后者。
6 结 论
本文依托阵列输出数据的稀疏表示模型,提出了一种WLS-IAE算法。详细分析了WLS-IAE算法的基本性能和计算复杂度,并与依赖于超参数的经典稀疏估计类算法l1-min的计算复杂度进行了比较。仿真结果表明:WLS-IAE算法在低SNR、单快拍、信号相干、目标信号空间间隔很小等非理想情况下都具有很好的估计精度和分辨率;WLS-IAE算法的计算效率明显高于一般的稀疏估计类方法。因此,WLS-IAE算法不仅保持了稀疏表示框架在非理想条件下的良好估计性能,而且避免了传统稀疏参数求解方法的高复杂度和经验公式的超参数选取问题,因此非常适用于快变目标信号DOA的实时跟踪测量,具有潜在的工程实用价值。

