基于Gabor框架的线性调频信号压缩采样与重构
孟 晨, 王 强,*, 王 成, 李一宁
(1.陆军工程大学石家庄校区导弹工程系, 河北 石家庄 050003;2.国民核生化灾害防化国家重点实验室, 北京 102205)
0 引 言
线性调频(linear frequency modulation, LFM)信号又称Chirp信号,是信号处理领域中常用的信号形式,在雷达、声呐等探测系统中,均得到广泛应用[1-3]。该类信号频带较宽,在Nyquist采样定理下,要保证信号的精确重构,采样频率至少是信号最高频率的两倍。因此,传统A/D转换器需要工作在极高的采样频率下,以保证信号在采样过程中不造成信息丢失。
压缩感知理论的产生,为宽带LFM信号的采集问题提供了一种新的思路[4-7]。在压缩感知理论框架下,信号的采集过程不再依赖于Nyquist采样定理,而是基于信号本身所具有的信息量,在信号采集的同时,实现信号的压缩。基于压缩感知理论,国内外学者对压缩采样的具体实现方式进行了研究,主要包括调制带宽转换器(modulated wideband converter, MWC)压缩采样系统[8-9]、随机解调(random demodulation, RD)压缩采样系统[10-11]以及Gabor框架压缩采样系统[12-13]。相比于MWC以及RD压缩采样系统,Gabor框架压缩采样系统能够利用信号在时频域所具有的稀疏性,实现较低的采样频率以及采样点数。因此,在LFM信号压缩采样中,具有极大的应用前景。
Gabor框架压缩采样本质上是对LFM信号时频系数的压缩采样。在重构过程中,首先利用采样点实现对时频系数的重构,再利用时频系数完成对LFM信号的重构,因此时频系数的精确重构是原始信号精确重构的先决条件。在Gabor框架压缩采样系统下,时频系数的重构过程是一个多观测向量(multiple measurement vectors, MMV)的重构问题[14-15]。目前,求解这一问题的典型算法包括:多重信号分类(multiple signal classification, MUSIC)算法[16-17]、同步正交匹配追踪(simultaneous orthogonal matching pursuit, SOMP)[18-19]、同步压缩传感匹配追踪(simultaneous compressive sampling matching pursuit, SCoSaMP)[20]以及多维扩展的稀疏贝叶斯学习算法(multiple response extension of sparse bayesian learning, M-SBL)[21-23]等。MUSIC算法能够以较低的采样率取得良好的重构效果,因此得到广泛应用,但是该算法要求原始信号稀疏矩阵非零行子矩阵为行满秩。而对于LFM信号,其时频系数矩阵非零行之间具有一定的相关性,因此时频系数的精确重构得不到保证。SOMP以及SCoSaMP算法是对单观测向量(single measurement vector, SMV)模型中,正交匹配追踪(orthogonal matching pursuit,OMP)以及压缩传感匹配追踪(compressive sampling matching pursuit, CoSaMP)算法的扩展,该类算法简单易实现、运算量少,但是在低采样率下极易陷入局部最优,重构误差较大。M-SBL是对SMV模型中稀疏贝叶斯学习(sparse Bayesian learning, SBL)算法[24-25]的扩展,该算法假设不同观测向量之间具有相同的稀疏分布模型,利用概率推理的方式估计模型参数。相比于SOMP以及SCoSaMP算法,M-SBL算法重构精确较高,重构效果较好。
鉴于M-SBL算法在求解MMV重构问题中所表现的优势,本文将M-SBL算法用于LFM信号时频系数的压缩采样重构过程中。在M-SBL算法下,稀疏矩阵的重构精度依赖于矩阵不同列向量之间的相关性。而对于LFM信号,其时频系数矩阵,相邻列向量之间具有一定的相关性,非相邻列向量之间相关性较差。因此,若直接采用M-SBL算法对LFM信号时频系数进行重构,则需要较高的采样点数来保证信号的重构精确,严重影响系统的压缩采样效果。
针对上述问题,本文研究了LFM信号压缩采样与精确重构方法。利用Gabor框架压缩采样系统,实现对LFM信号的压缩采样,以降低采样频率;引入M-SBL算法,求解重构过程中存在的MMV重构难题;针对LFM信号时频系数矩阵非相邻列向量之间相关性较差的问题,提出基于优化分类的信号重构方法,保证在较低的采样点数下,实现对LFM信号的精确重构。
1 Gabor框架压缩采样系统
1.1 Gabor变换及Gabor框架
Gabor变换[26-27]是一种广泛使用的线性时频分析方法,对于连续时间信号x(t)∈L2(C),Gabor变换系数可以表示为
(1)
式中,MblTakg=g(t-ak)ej2πblt为时频平移算子,a、b分别为时、频平移参数。Gabor变换系数zk,l本质上是信号x(t)在时频栅格(ak,bl)处的短时傅里叶变换,窗函数为g(t)。
为保证Gabor变换后,原始信号能够得到重构,定义Gabor框架[20,28-29]如下。
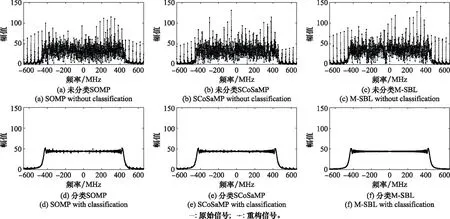
定义1对于任意的连续时间信号x(t)∈L2(C),若存在常数0 (2) 则称G(g,a,b)为Gabor框架,其中A1、A2分别为Gabor框架上下界。 给定窗函数g(t)、时频平移参数后,若Gabor框架条件得到满足,则存在对偶窗函数γ(t),使得信号x(t)能够表示为 (3) 与短时傅里叶变换相对比,Gabor变换使用了离散的时频栅格来对信号进行处理,同时Gabor框架的存在,保证了原始信号能够通过变换后的系数得到完全重构。而对于有限时频域支撑的信号,这种离散的时频栅格使得信号能够在有限的时频系数下进行展开。 假设信号时域支撑为[0,T],根据不确定性原理,其频域无限支撑。但考虑到信号能量主要分布在有限的频带范围内,因此定义信号本质带宽F=[Ω1,Ω2],满足 (4) 式中,X(f)为信号x(t)的傅里叶变换;Fc表示F以外的频带;òΩ<1。则信号在对偶窗函数γ(t)下的展开可以近似为 (5) 若窗函数g(t)在[0,Wg]上紧支撑,本质带宽为[-Ωg,Ωg],则K1、K2、L1、L2可以表示为 ⟹ (6) 对于有限时域支撑的LFM信号,图1给出了该信号在Gabor变换下的时频特性图。其中,图1(a)为LFM信号时域波形,图1(b)为LFM信号在Gabor变换下的时频特性。 图1 LFM信号时频特性 可以看出,LFM信号在Gabor变换下具有良好的稀疏性。利用这种稀疏性,本文引入了Gabor框架压缩采样系统,实现对LFM信号的压缩采样。 Gabor框架压缩采样系统由Eldar团队于2012年提出[12],该系统模型结构如图2所示。 图2 Gabor框架采样系统模型结构 图2中,输入信号x(t)同时进入JM个通道,在第(j,m)个通道中,x(t)首先和函数qj,m(t)=wj(t)sm(t)相乘,再利用积分器完成积分,其中0≤j≤J-1,0≤m≤M-1,且j,m∈Z。函数qj,m(t)根据Gabor框架G(g,a,b)进行设计,其表达式为 qj,m(t)=wj(t)sm(t) (7) (8) 式中,wj(t)为频域调制函数;sm(t)为时域调制函数。x(t)经过第(j,m)个通道后进行采样,每一个通道上的测量值可以表示为 (9) 通过采样系统获得测量值yj,m后,可以根据调制函数中的djl和cmk等参数信息求解出Gabor系数zk,l,再利用式(5)重构出原始信号。 为求解Gabor系数zk,l,将式(9)写成矩阵形式: Y=DUT,U=CZ (10) 式中,Y为J×M维矩阵,第(j+1,m+1)个元素为yj,m;假设L=L2-L1+1,K=K2-K1+1,则U是M×L维矩阵;Z为K×L维Gabor系数矩阵,其l-L1+1列为Z·l-L1+1=[zK1,l,…,zK2,l]T,C为M×K维测量矩阵,其(m+1,k-K1+1)处元素为cmk;D为J×L维矩阵,其(j+1,l-L1+1)处元素为djl;C和D的选择要保证能够从Y中恢复出Z;如果J=L,M=K,且C和D为单位矩阵,则本文采样系统就是标准的无压缩的Gabor框架采样系统。 为简化电路设计,令J=L且D=I,则式(10)可以简化为U=CZ,其中U=YT。由于LFM信号Gabor系数矩阵具有良好的稀疏性,因此可以通过重构算法,实现对Gabor系数矩阵的精确重构,该过程是一个MMV重构问题,即 s.t.U=CZ (11) 式中,supp(·)表示求支撑集。完成矩阵Z的重构后,即可通过式(10)重构出原始信号。 针对上述MMV重构问题,本文提出了基于M-SBL的求解方法[21-22]。考虑到压缩测量过程可能存在的噪声干扰,U可以表示为 U=CZ+n (12) 假设U·l为矩阵U的第l-L1+1列,则 U·l=CZ·l+n·l (13) 为简化分析过程,假设噪声为零均值高斯噪声,噪声方差为σ2,则U·l的条件分布概率密度函数为 (14) 对于Gabor系数矩阵,其第k-K1+1行向量Zk·的先验稀疏分布为高斯分布,方差为γk,即 p(Zk·|γk)=N(0,γkΙ) (15) 则系数矩阵Z的先验分布可以表示为 (16) 式中,γ为超参数向量,γ=[γK1,γK1+1,…,γK2]T。利用式(14)和式(16),Z·l的后验分布可以表示为 (17) 式中,均值和方差分别为 M=[μ·L1,μ·L1+1,…,μ·L2] (18) (19) 式中,Γ=diag(γ);Σt=σ2I+CΓCT;M为对Gabor系数矩阵Z的估计。参数σ以及超参数向量γ可通过最大化边缘似然函数获得,即 (20) 具体推导过程可参考文献[21],其参数估计结果为 (21) (22) 从上述分析可以看出,M-SBL算法重构过程中假设Gabor系数矩阵Z中各行服从同一高斯分布。从另一角度来说,要满足这种分布特性,Gabor系数矩阵Z中各列之间需要具有很强的相关性。而对于LFM信号,其Gabor系数矩阵特性如图1所示,可以看出,Z中只有相邻列之间具有一定的相关性,而非相邻列之间相关性变小,并且间隔距离越大,相关性越小。LFM信号这一特点使得M-SBL算法直接用于求解式(11)时,重构效果较差,要保证较小的重构误差,只能通过增加采样点数,这就严重影响了压缩采样系统的压缩率。 针对这一问题,本文提出了基于优化分类的LFM信号压缩采样重构方法,该方法以M-SBL算法为基础,利用U中的信息,对各个列向量进行分类,再利用M-SBL算法逐类进行压缩采样重构。 U中的每个列向量,表示压缩采样系统对Gabor系数矩阵Z中相应列向量的采样结果,因此对U的分类,也实现了对Gabor系数Z的分类。而分类的目的是要保证Gabor系数子矩阵(由Z中同属一类的列向量组成)各列之间具有良好的相关性。从而可以假设该子矩阵中各列具有相同的稀疏先验分布模型,并利用M-SBL算法对该子矩阵进行重构。 LFM信号Gabor系数矩阵Z中相邻列之间具有一定的相关性,利用这一特点,本文将U中列向量的分类问题转化为列向量的分割问题,以保证Gabor系数子矩阵各列在原Gabor系数矩阵Z中的相邻性。假设分类个数为N,定义分割位置集合p={p1,p2,…,pN+1},其中: (23) 式中,元素pi(2≤i≤N)表示第i-1类与第i类之间的分类位置,则p中N+1个元素将U中列向量分为N类。同时,同类列向量之间的相邻性也保证了所对应的Gabor系数子矩阵各列之间相邻。 为保证分类效果,本文引入目标函数来优化分割位置。首先,定义相关性参数来衡量U中同类列向量之间的相关性。对于U中任意两列向量,相关性参数定义为 (24) 其中 (25) 为衡量同类列向量之间的相关性,定义分类中心向量为 (26) 式中,Li=pi+1-pi,则同类列向量之间的相关性可以表示为 (27) 令rmin=min{r1,r2,…,rN},则优化目标函数可以表示为 (28) 上述目标函数可以通过优化算法进行求解,如粒子群优化(particle swarm optimization, PSO)算法以及量子粒子群优化(quantum particle swarm optimization, QPSO)算法[30-31]等。优化过程中,以集合p中N-1个元素pi(2≤i≤N)为待优化参数,以式(28)为目标函数,输出最终的分割位置pi,实现最佳的分类方式。 综上所述,本文基于优化分类的M-SBL重构算法如算法1所示。 算法1基于优化分类的M-SBL重构算法 输入:矩阵U,矩阵C; 输出:Gabor系数矩阵Z′; 步骤1QPSO优化分类 步骤1.1以p中N-1个元素为待优化参数,初始化粒子位置以及速度; 步骤1.2根据式(27)计算同类列向量的相关系数,确定粒子群中全局最优位置以及每个粒子局部最优位置; 步骤1.3更新粒子位置以及速度信息; 步骤1.4判断是否满足迭代终止条件,满足则给出最优的分割位置集合p,否则返回步骤1.2。 步骤2M-SBL逐类重构 步骤2.1根据步骤1中的最优分割位置集合p对U进行分类,并逐类运行步骤2.2~步骤2.5; 步骤2.2初始化稀疏先验分布参数以及噪声方差; 步骤2.3利用式(18)和式(19)完成对稀疏系数均值与方差的估计; 步骤2.4利用式(21)和式(22)完成分布参数的更新; 步骤2.5判断是否满足迭代终止条件,满足则利用均值给出重构的Gabor系数子矩阵,否则返回步骤2.3; 步骤2.6对子矩阵进行重新组合,输出Gabor系数矩阵Z′。 得到重构的Gabor系数矩阵Z′后,可在Gabor框架下,完成对原始LFM信号的重构。LFM信号的整个压缩采样与重构流程可以表述为图3的形式。首先,利用Gabor框架压缩采样系统完成LFM信号压缩采样,并通过离散的采样点构造矩阵U;然后利用矩阵U和矩阵C以及本文基于优化分类的M-SBL重构算法完成重构过程,获得Gabor系数矩阵Z′;最后,利用矩阵Z′,在Gabor框架下,完成对原始LFM信号的重构。 图3 LFM信号压缩重构流程 相比于未经分类优化的重构算法相比,本文基于优化分类的LFM信号压缩采样重构方法在一定程度上增加了重构过程复杂度。但是,该重构方法仍然较高的应用价值。一方面,LFM信号在时频域所具有的特点,使得其在未经分类的条件下,Gabor系数矩阵非相邻列之间相关性较差,联合稀疏度较大。要保证原始信号的精确重构,就需要增加采样点数,这就会导致前端压缩采样系统压缩效率较差。而基于优化分类的重构方法能够有效减少前端压缩采样系统对采样点数的需求,降低存储空间与传输压力。另一方面,本文优化分类的重构过程通常在后端服务器内运行,而后端服务器强大的运算能力能够支持更为复杂的重构算法,因此在实际应用过程中,计算复杂度增加的问题,能够得到很好的解决。 为验证本文算法的有效性,利用LFM信号进行仿真实验。仿真LFM信号表达式为 (29) 式中,f0为中心频率;k为调频率。实验过程中,利用式(29)产生两种LFM信号,信号参数设置如表1所示,信号时域波形以及频谱如图4所示。两种LFM信号时域支撑均为[0, 1 μs],本质带宽分别为[-420 MHz, 420 MHz]、[-620 MHz, 620 MHz]。 表1 两种LFM信号参数设置 图4 仿真信号 针对上述LFM信号,利用Gabor框架压缩采样系统对信号进行压缩采样。采样系统中cmk为伪随机数,g(t)为高斯窗函数,窗函数时域波形以及频谱如图5所示,该窗函数在[0, 0.075 μs]上紧支撑,本质带宽为[-60 MHz,60 MHz]。压缩采样系统时、频平移参数设置为0.025 μs、40 MHz。则对于上述两种LFM信号,时频表示参数设置如表2所示。 图5 窗函数 表2 两种LFM信号时频参数设置 利用LFM信号在Gabor变换下的稀疏性,对信号进行压缩采样。设置压缩采样通道个数为ML,则采样点数为ML,单通道采样频率为1 MHz。而在Nyquist采样定理下,两种信号的最低采样频率分别为840 MHz、1 240 MHz。可以看出压缩采样系统的采样频率远远低于信号的Nyquist采样频率。 利用压缩采样系统输出的采样点,对原始信号进行重构。为验证本文基于优化分类的M-SBL重构算法的有效性,引入不同重构算法进行LFM信号压缩采样重构对比实验。对比算法包括SOMP以及SCoSaMP。为有效衡量重构效果,引入相对误差(relative error, RE)作为重构误差量化指标。RE表达式为 (30) 式中,x′为重构信号。每种算法进行500次蒙特卡罗实验,当重构信号误差低于0.01时,认为信号得到精确重构。根据经验值,两种信号的分类个数分别设定为5、8。实验中采用QPSO对压缩采样点U进行分类,并逐类进行重构,则不同算法精确重构概率如图6所示。 图6 不同算法重构概率 对比两种信号可以看出,在相同M值条件下,信号2的重构概率要高于信号1。分析其原因,主要是信号2调频率k要高于信号1。在相同的采样系统参数设置下,信号2调频率的提高使得信号时频域的稀疏度降低、稀疏性得到改善。因此在相同M值条件下,信号2的重构概率要高于信号1。对比不同算法可以看出,M-SBL重构概率要高于SOMP以及SCoSaMP。在经过优化分类后,U中同类列向量所对应的Gabor系数子矩阵联合稀疏度降低,因此更有利于Gabor系数矩阵的精确重构。同时,基于目标函数的优化分类过程,保证了Gabor系数子矩阵各列之间具有良好的相关性。相比于SOMP以及SCoSaMP算法,M-SBL算法能够有效利用子矩阵各列之间的相关性,因此在相同的M值条件下,其重构概率更高。 在保证重构概率不低于95%的条件下,两种信号的最低M取值分别为27、17。此时系统采样点数分别为621、561。而在Nyquist采样定理下,两种信号的最低采样点数分别为840、1 240。因此可以看出,本文Gabor框架压缩采样系统不仅大大降低了采样频率,还压缩了采样点数。同时,LFM信号调频率越高,压缩效果越明显。 为进一步验证分类优化方法的有效性,利用压缩采样系统输出,在未经分类的条件下,利用3种算法对原始信号进行重构,并与分类条件下的重构效果进行对比。对于信号1,实验过程中分别设置M=27、32、37,此时基于分类优化的M-SBL算法重构概率高于95%。在未分类以及分类的条件下,利用3种重构算法对信号1进行重构,为方便观察原始信号中不同频率成份的重构效果,图7~图9给出了原始信号与重构信号频谱。 图7 不同算法重构效果(信号1,M=27) 图8 不同算法重构效果(信号1,M=32) 图9 不同算法重构效果(信号1,M=37) 同样,对于信号2,实验过程中设置M=17、22、27,以保证基于分类优化的M-SBL算法重构概率高于95%。在未分类以及分类的条件下,利用3种重构算法对信号2进行重构,其原始信号与重构信号频谱如图10~图12所示。对于不同的重构信号,利用式计算重构RE,计算结果如表3所示。 图10 不同算法重构效果(信号2,M=17) 图11 不同算法重构效果(信号2,M=22) 图12 不同算法重构效果(信号2, M=27) 表3 不同算法重构相对误差对比 从实验结果可以看出,对于上述两种LFM信号,未经分类的SOMP、SCoSaMP以及M-SBL算法均不能够有效重构原始信号。尽管随着M的提高,重构效果有所改善。但是体现在RE值上,当M值较大时(信号1中M=37时,信号2中M=27时),3种重构算法RE仍大于0.1。相比于未经分类的信号重构算法,经过分类后,不同算法的信号重构效果明显改善。当M较大时,3种算法均能够保证重构相对误差RE低于0.01,重构效果较好。分析其原因,主要是因为在未经分类条件下,LFM信号在Gabor变换下的系数矩阵联合稀疏度较高,稀疏性较差,在这种条件下,SOMP、SCoSaMP以及M-SBL算法并不能够有效重构原始信号。而通过优化分类的方式,使得矩阵U中同类列向量所对应的Gabor系数子矩阵联合稀疏度降低,因此3种算法的重构效果得到明显改善。同时,与图6中实验结果类似,由于M-SBL算法在重构过程中利用了Gabor系数子矩阵各列之间的相关性,因此重构效果最佳,重构相对误差RE最低。 基于Gabor框架的压缩采样系统在工作过程中,不可避免地存在噪声干扰,为此对压缩采样过程添加不同信噪比(signal to noise ratio, SNR)的噪声,分析噪声对压缩采样系统以及重构过程的影响。实验过程中,重构算法采用的是本文所提的基于优化分类的M-SBL算法。对于信号1,M分别设置为27、32、37,对于信号2,M分别设置为17、22、27。此时,在不含噪声条件下,原始信号重构概率均高于95%。则在添加噪声后,信号的重构概率如图13所示。 从图13中可以看出,当SNR≤11 dB时,两种信号在不同M值条件下,重构概率均为0。当SNR>11 dB时,随着的增加,信号重构概率逐渐升高。当SNR>20 dB时,两种信号的重构概率均稳定在95%以上。同时,从实验结果可以看出,在含噪条件下,提高M值,能够有效改善重构效果。例如,对于信号1以及信号2,M值分别为37、27时,重构概率曲线最先趋于稳定。此时,在保证信号高概率重构的条件下,系统所能允许的噪声强度最大,即抗噪声干扰能力最强。因此,在实际应用过程中,可以通过适当提高采样点数的方法来抑制噪声对系统工作的影响。 图13 噪声对重构概率的影响 在传统的基于A/D转换器的信号采集方法下, LFM信号需要极高的采样频率以保证采样过程不造成信息丢失。针对这一问题,本文提出了一种基于Gabor框架的LFM信号压缩采样与重构方法。Gabor框架采样系统用于实现对LFM信号的压缩采样,在该系统下,LFM信号的采样频率与采样点数均低于传统采样方法。利用压缩的采样点,本文提出了基于优化分类的LFM信号重构方法,通过分类,保证了Gabor系数子矩阵各列之间具有良好的相关性。再利用M-SBL算法进行逐类重构,改善LFM信号重构效果。通过仿真实验,验证了本文LFM信号压缩采样与重构方法的有效性。

1.2 压缩采样系统


2 基于优化分类的LFM信号重构
2.1 压缩采样系统重构模型
2.2 M-SBL算法
2.3 优化分类方法



3 仿真实验
3.1 仿真LFM信号


3.2 LFM信号压缩采样


3.3 LFM信号重构效果对比







3.4 噪声对重构过程的影响

4 结 论

