高移动性Jakes信道的学习与估计
邵 凯, 陈连成, 刘 胤
(1.重庆邮电大学通信与信息工程学院, 重庆 400065; 2.移动通信技术重庆市重点实验室,重庆 400065; 3.移动通信教育部工程研究中心, 重庆 400065)
0 引 言
随着中国高铁系统的大规模部署以及高速公路的快速发展,高移动场景条件下的无线通信系统受到了越来越多的关注。在高移动性环境中,无线信道受到多径效应和多普勒频移的影响,具有快时变和非平稳特性[1]。正交频分复用(orthogonal frequency division multiplexing,OFDM)技术在第4代移动通信中的成功应用,检验了其抗频率选择性衰落特性,成功应用于多种高数据速率通信标准。但是,随着移动端速度的加快,信道状态的快速变化引起严重的载波间干扰(inter carrier interference,ICI),从而导致在高移动环境下,传统的信道估计算法性能较差。因此高移动环境下如何完成可靠的信道估计是亟待解决的重要问题。
传统信道估计算法可大致分为两类:信道盲估计和基于导频辅助信道估计。因为高速移动场景下信道变化的速度快于盲信道估计的收敛速度,其算法性能下降严重,一般认为信道盲估计方法不适用于高速移动环境。基于导频辅助信道估计的算法有最小二乘(least square,LS)算法[2]、线性最小均方误差(linear minimum mean square,LMMSE)算法[3]等。这类方法假设信道频率响应(channel frequency response,CFR)在一个符号周期内不发生改变,且相邻OFDM符号间的CFR是线性变化的。由于多径和多普勒频移的共同影响,信道变化相对复杂,线性变化的假设不适用于高移动信道,导致传统插值算法性能下降严重,信道估计的精度下降。为弥补传统信道估计算法在高移动场景下的误差,文献[4]提出基扩展模型(basis expansion model,BEM)的信道估计方法。其思想是将一个OFDM符号内信道冲激响应(channel impulse response,CIR)的参数数量减少为信道多径数目与基函数个数的乘积,通过构造BEM将CIR转换为由基本矢量形成的低维空间进行降维,减少CIR估计参数。文献[5]采用复指数函数BEM表示时域信道,信道估计问题转换为基模型系数估计,且通过LS或LMMSE算法估计基系数。文献[6]提出针对BEM下的非线性信道状态空间模型,采用无迹卡尔曼滤波(unscented Kalman filter,UKF)方法进一步跟踪信道响应提升估计精度。基于BEM的方法根据采用基函数的不同会导致估计误差增加或估计复杂度太高,限制模型实用性。因此,快时变信道下的信道估计仍面临挑战。
深度学习(deep learning,DL)的方法在计算机视觉、图像处理等领域的应用取得了巨大的成功,最近还被成功应用到无线通信中[7]。由于DL算法在信号分类[8]、信号检测[9]、信道编码[10]、信道状态信息反馈[11]等的优异表现,研究人员将DL方法应用在信道估计[12]中。对于信道估计,DL方法可粗略分为两类:一类是使用神经网络学习信道的变化特征,进而从导频信号估计完整信道[13]。文献[14]提出了一种基于模型驱动的OFDM接收机,利用专家知识构建网络,其模型性能更加良好,且收敛速度更快。文献[15]针对双选择性衰落信道提出了一种基于深度神经网络的在线估计方法,其设计预训练进一步提高估计器性能,结果表明其性能优于基于BEM的信道估计方法。文献[16-17]提出联合卷积神经网络(convolution neural networks, CNN)和循环神经网络相结合的信道估计网络,这种方法相较传统方法具有更好的鲁棒性,并提升了估计精度。此类方法大多使用基于数据驱动的方式,需要大量训练数据,导致模型训练代价较大,且复杂度大。另一类是将信道状态信息看作图像,利用图像处理技术恢复信道。文献[18]首次提出将信道矩阵看作二维(2-dimensional,2D)自然图像,结合图像重建技术进行信道估计的思想。文献[19]在其基础上提出信道估计网络ChannelNet,但其只用单层卷积层(convolution, Conv)完成特征提取,且卷积核较大,存在感受域较小的问题,特征提取具有局限性,而且ChannelNet只使用单层非线性映射,导致参数过多、结构较为简单、重建性能较差,估计性能有待提升。
高速移动场景信道矩阵中,元素的联系性表现为局部紧密,传输距离越远相关性越弱。通过识别相邻元素之间细致的相关性可以提高信道估计性能。因此针对文献[19]所提出结构的不足,本文将信道矩阵转化为2D自然图像,提出由快速超分辨CNN(fast super-resolution CNN, FSRCNN)[20]和去噪CNN(denoising CNN, DnCNN)[21]组成的FSR-Net。首先,FSRCNN网络有以下优点:① 调整特征提取层,减小卷积核大小,增大感受野,加快收敛速度;② 针对CIR估计参数过多问题,设计收缩层对估计参数降维;③ 将单层非线性映射用多个小层代替,增加了更多的映射层,加深网络深度的同时又增强网络的容量。其次,针对信道受到高斯噪声和ICI的影响,使用DnCNN降低噪声和ICI影响。总而言之,本文所提FSR-Net网络利用FSRCNN对信道插值过程进行建模,获得信道矩阵的初步估计,然后利用DnCNN进一步减少信道噪声和ICI影响并精细化粗略结果,提升信道估计准确度。仿真结果表明,所提出FSR-Net网络估计性能优于传统的信道估计算法和基于DL的最新方法,并有效降低了信道估计的复杂度。
1 系统模型
1.1 高移动Jakes信道模型
无线信道是分析通信系统性能的基础[22]。在文献[23]中综合考虑影响高速移动无线信道因素的电波传输环境,分析多种不同模型性能的优劣。结合实际信道建模的合理需求以及研究的广泛性,本文选择文献[23]中改进Jakes模型作为研究的样本。
假设在高移动场景中,基站处于静止的状态,而接收端以稳定的速度沿着固定的方向行驶。由于信号传播存在着明显的直射径,因此传播信道服从莱斯衰落,仿真模型可以写为
h(t)=
(1)
zl(t)=2πfdtcos(αl(t))+φl
(2)
z0(t)=2πfdtcos(α0(t))+φ0
(3)
式中,L为多径数;φl为第l条散射径的相位;K为莱斯因子;αl(t)的表达式为
(4)
式中,θl表示第l条散射径的到达角,θl和φl统计独立并且在[-π, π]上均匀分布;多普勒频移fd表示为
fd=fmcosθl(t)
(5)
式中,fm=vfc/c为最大多普勒频移,其中fc为载波频率,v为移动端速度,c为光速。φ0和θ0是直射径的初始相位和到达角,到达角θ0(t)可以表示为
(6)
(7)
式中,Ds是接收端离基站的初始垂直距离;Dmin是基站与轨道的最小距离。
1.2 高移动Jakes信道特性分析
在OFDM系统中,发送端经过串并转换后,OFDM的第k个子载波上的符号表示为X(k),通过N点快速傅里叶变换调制之后,时域发送信号x(n)可表示为
(8)
发送信号x(n)经过信道后,在接收端的时域信号y(n)可表示为
n=0,1,…,N-1
(9)
式中,N是所有子载波数;wn是加性高斯噪声信号;h(n)是信道的时域表示。
1.2.1 非平稳性
经过对式(9)分析可知,其信道的时域自相关函数可写为
Rhh(τ)=
[Jo(2πfdτ)+Kcos(2πfdτcos(θ0(t)))+
jKsin(2πfdτcos(θ0(t)))]/1+K
(10)
式中,Jo(·)表示0阶贝塞尔函数。由式(10)可知,随着时间和位置变化,导致信号的到达角θ0(t)发生改变,高移动环境下信道的时域自相关函数是时变的,说明了信道具有明显的非平稳特性。在传统信道估计方法中,假设数据符号间的信道时域相关性是不变的,即信道是广义平稳的。然而,在高移动环境下信道具有明显的非平稳特性,使传统插值方法的性能受限,导致信道估计精度下降。
1.2.2 快时变特性
经过对式(9)的快时变性进行分析,h(m-n)表示为第m个子载波对第n个子载波的ICI系数,可写为

(11)
式中,fdT是归一化多普勒频率。
对于第n个子载波的目的信号功率可以表示为
E[|C(n)|2]=E[|x(n)h(n)|2]
(12)
而ICI的功率可表示为
(13)
式中,传输信号是零均值并且统计独立,则载干比(carrier to interference ratio, CINR)可表示为
(14)
式(14)说明CINR是子载波数N和归一化多普勒fdT的函数,而相关研究表明,子载波N的改变对CINR的影响很小。因此,高移动环境下,随着速度增加,归一化多普勒频移相应加大,CINR减小,导致快时变特性引入ICI,降低估计准确度,降低系统性能。
2 FSR-Net的信道估计
2.1 FSR-Net网络结构
FSR-Net的结构如图1所示。通过LS方法得到导频处的信道矩阵,将其看作为2D自然图像,经过FSR-Net网络进行处理。其中,FSR-Net网络分两个阶段:① 利用FSRCNN对原始的信道图像进行特征提取及信道插值完成建模,以实现低分辨率到高分辨率的重建任务,得到粗略的信道图像;② 为移除信道图像中信道噪声和ICI的影响,通过级联去噪网络处理。

图1 FSR-Net结构图
2.1.1 FSRCNN
对于FSRCNN,其结构如图2所示。

图2 FSRCNN网络结构
首先,使用卷积核大小为5×5的Conv进行特征提取,其思想是捕捉最重要的信道状态特征图。由这些特征图构成下一层的输入,并传递到完全连接的Conv,其变换公式为
H1=f(W1*H0+b1)
(15)
式中,f(·)表示激活函数;b1表示偏置项;*表示卷积;W1表示第1层的权值向量;H1表示第1层输出的特征图;H0表示输入数据。所有Conv使用的激活函数为参数校正线性单元(parametric rectified linear unit, PReLU),其通过将非线性因素引入神经元,将线性输入信号转换为非线性输出信号,以便神经网络可以任意近似任何非线性函数。其表达式为
PReLU(H1)=max(0,H1)+∂min(0,H1)
(16)
式中,∂表示随机参数。对于剩下的Conv操作,其步骤与式(15)和式(16)类似。接下来使用卷积核大小为1×1的Conv进行减小维度,减少CIR的估计参数,以降低映射的计算复杂度。中间使用多个连续Conv进行线性映射,卷积核大小为3×3,目的是加深网络结构,减少插值算法带来的误差,提高信道图像重建的准确性。实验表明,少量的非线性映射网络能表现出良好的性能,而添加更多的非线性映射网络并不能显著提高重建质量,反而会增加计算复杂度。然后,使用卷积核大小为1×1的Conv进行维度扩展,以扩展高分辨率的特征维度,提高信道图像重建的精度。最后使用卷积核大小为9×9的Conv进行信道图像的重建,利用较大的感受域来提高信道图像重建的准确度。用P表示所有层数,重建结果可表示为
H′=f(WP*HP-1+bP)
(17)
式中,H′为重建后带有噪声的信道图像矩阵;HP-1为第P-1层的输出;WP为第P层的权值向量;bP为第P层的偏置顶。
2.1.2 DnCNN
FSR-Net网络使用的去噪器在信道估计中起关键作用。去噪器要消除噪声和ICI带来的影响,提高信道图像的准确度。因此,使用DnCNN去噪器,其结构如图3所示。
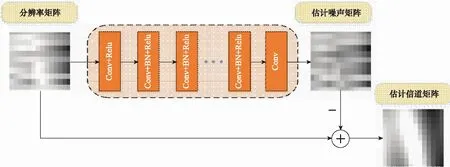
图3 DnCNN网络结构
在图像去噪领域,DnCNN因其网络架构和训练方面的强大建模能力得到广泛应用。其放弃对去噪图像映射的直接学习,而学习其中的残余噪声。这种剩余学习方法可消除高度结构化的自然图像噪声。同时,DnCNN去噪器可以很好地处理噪声水平未知的去噪问题,解决随模型加深神经网络梯度消失和退化的问题,能够自动判断冗余层完成恒等映射,且不会产生额外的参数和计算复杂度。
本文DnCNN由20层卷积组成,使用卷积核大小为3×3的卷积网络,其中激活函数为线性整流单元(rectified lineer unit, ReLU),卷积网络结构为Conv+ReLU。中间18层使用64个尺寸大小为3×3的卷积核,包括批归一化层(batch normalization, BN),结构为Conv+BN+ReLU。最终Conv使用大小为3×3的卷积核来重建信号。通常,目的是建立一个映射关系,即
H″=f(H′,W)
(18)
式中,
H′=H″+WZ
(19)
H″表示期望输出信道图像矩阵;W表示学习的权重参数集;Z表示为剩余噪声矩阵。神经网络将带有噪声信道图像H′作为输入,并产生剩余噪声Z,而不是估计的信道图像矩阵H″作为输出。其最后重建的信号可表示为
Z=f(H′,W)
(20)
最终输出可表示为
H″=H′-Z
(21)
因此,通过引入剩余学习方法可提高网络训练准确性,且收敛性更快。
2.2 模型训练
为离线训练FSR-Net网络,本文模拟生成随机数据序列作为传输符号,添加导频符号形成相应OFDM帧,并在训练和测试阶段固定导频符号。根据信道路径增益计算出全资源网格的信道频率响应的最优估计H。将导频位置的信道估计值HP和最优估计H收集为训练数据,对模型进行训练以最小化神经网络输出与标签数据之间的差异。
通过FSR-Net网络获得的信道矩阵过程可表示为
H″=f(W,HP)
(22)
网络的总损耗函数是估计信道响应与实际信道响应之间的均方误差(mean square error, MSE),计算结果为
(23)
式中,S为所有训练样本集的总的样本数。为加快训练收敛性,采用自适应矩估计(adaptive moment estimation, Adam)算法更新FSR-Net网络的参数集。Adam算法通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计独立的自适应学习率。
3 仿真分析
为了较全面评估信道估计性能,本文将FSR-Net与ChannelNet[19]分别在时域和频域进行了仿真比较。两种方案都在相同的设置条件下应用相同的数据集完成训练:训练集、验证集和测试集的大小分别为45 000、3 000和2 000。在频域方案测试时,收集通过LS算法[2]得到的信道状态信息为数据集,测试结果与经典的LS[2]和LMMSE[3]对比。而对于时域方案测试,收集通过BEM-LS[5]得到的信道状态信息为数据集,测试结果与BEM-LS[5]和BEM-UKF[6]对比。初始的训练学习率设为0.001,随着训练轮数的增加,逐渐降低训练学习速率。最小批量大小为256,其根据不同的训练集而灵活配置。
所有仿真随机生成二进制比特流,采用16QAM的星座调制和Jakes信道模型(共5个抽头,均具有Jakes多普勒功率谱)。
为公平比较,使用归一化MSE(normalized MSE, NMSE)来衡量性能。NMSE的定义为
(24)
3.1 频域测试
图4和图5分别给出了不同移动速度下信道频域估计的测试结果。速度为50 km/h时,LMMSE算法的信噪比(signal to noise ratio, SNR)增益比LS算法高大约8 dB左右,这是由于LS算法忽略了噪声的影响,而LMMSE算法充分利用了信道的二阶统计特性信息,提高了估计的精度。ChannelNet网络的SNR增益比LMMSE算法高大约12 dB左右。而本文所提出的FSR-Net比ChannelNet的SNR增益提升了大约5 dB左右,是因为在设计FSR-Net网络结构时增加了更多的映射层,同时选取了更小的卷积核,加深了网络深度的同时又增强了网络的容量,使其能够更好地学习信道矩阵内元素之间的相关性,使其性能优于ChannelNet。速度为300 km/h时,LS算法和LMMSE算法的性能表现出比较差的NMSE,主要原因是高速变化的信道环境的相关系数是时变参数,并且信道状况的变化规律不符合线性假设,导致了信道估计的精度下降,表明LS算法和LMMSE算法并不适用于高速移动环境。而本文提出的FSR-Net方法,相比于传统的频域信道估计算法和ChannelNet网络表现出更加优异的SNR增益和NMSE性能,因此更适合于高速场景,并且在低速环境中同样表现出色。
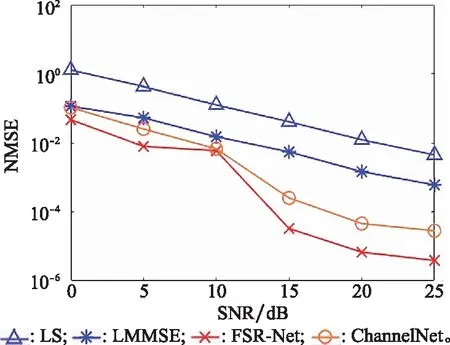
图4 速度为50 km/h时的频域估计算法比较

图5 速度为300 km/h时的频域估计算法比较
3.2 时域测试
图6和图7分别给出了不同移动速度下信道时域估计的测试结果。

图6 速度为50 km/h时的时域估计算法比较

图7 速度为300 km/h时的时域估计算法比较
速度为50 km/h时,BEM-LS算法和BEM-UKF算法的NMSE性能相近,ChannelNet方法在低SNR时性能较差,随着SNR的增加,ChannelNet的性能逐渐提高。而本文提出的FSR-Net方法,从低SNR到高SNR的NMSE性能都优于传统方法和ChannelNet方法。
速度为300 km/h时,除了BEM-LS算法的NMSE性能下降外,其他方法的性能基本没有降低,但本文提出的FSR-Net方法表现出更加优异的效果。因此,该方法在时域估计方面也具有很高的性能。
3.3 复杂度比较
表1给出了本文所涉及算法的复杂度分析,其中Q表示基函数的个数,L表示多径数。通常,QL远远小于子载波数N。对于基于DL的算法,通常以网络前馈运行所需的乘法和加法次数为复杂性度量,即在线估计复杂度。

表1 算法复杂度对比
由表1可知,ChannelNet和FSR-Net在线估计复杂度低于LMMSE算法和BEM-UKF算法,但高于LS算法和BEM-LS算法。对于在线估计阶段,神经网络已被训练并直接用于信道估计,而且ChannelNet和FSR-Net只涉及到矩阵的乘法和加法运算,并不涉及矩阵求逆运算,因此总体复杂度较低。本文所提FSR-Net算法复杂度与ChannelNet算法类似,但FSR-Net性能比ChannelNet更加优异。综合考虑复杂度与性能比较,所提FSR-Net算法以较小的复杂度代价获得了更好的系统性能。
4 结 论
本文针对高移动场景下传统的信道估计算法复杂度过高及估计精度较差的问题,提出基于DL的信道估计网络。所提的FSR-Net具有大感受域、高收敛速度、训练参数少等特点。根据高移动性Jakes信道矩阵中局部相关特性,FSR-Net应用大感受域的快速超分辨神经网络进行特征提取及信道插值完成建模,同时针对时域情况下估计参数较多的问题,利用所设计的收缩层对估计参数进行降维,并应用去噪神经网络消除信道噪声的影响,降低信道估计的复杂度。仿真结果表明,所提的FSR-Net方法不论在时域还是频域测试下,都比传统的方法和基于DL的方法性能优异,并且有效降低了计算复杂度。

