球带上LAPLACE算子第一特征值的一些性质*
吕 康,黄振友
(南京理工大学 理学院,南京 210094)
0 引 言
考虑
Δu+λu=0
(1)
u=0,∀x∈∂Ω
(2)
其中,Ω为三维欧氏空间单位球上的球带,Ω={x:ξ≤φ≤η,0≤θ≤2π}。上述问题有可数个单调递增的特征值满足:
0<λ1<λ2≤…≤λn≤…
且λn→∞(n→∞)(称λ1为第一特征值或最小特征值)。由最大-最小原理,对于比较靠前的特征值相对来说更容易处理。尤其是λ1,λ2,它们与粒子在某一场中运动所具有的能级有关[1]。SHEN和SHIEH[2]得到当Ω的面积不变,ξ逐渐增加时式(1)(2)的最小特征值严格增加的结果,且当Ω关于赤道平面对称时达到最大;SHIEH[3]得到当Ω面积在小于等于2π时,第二特征值也在它关于赤道平面对称的时候最大(但是这里并没有得到单调性);RAMM和SHIVAKUMAR[4]考虑Ω=D1(0)Dr(h),其中 0 考虑 (3) 假设Ω的面积为S=2πA,考虑当A固定,随着ξ的增加,式(3)的第一特征值λ1的变化趋势是怎样的。对于式(3)中的Robin型边条件,不难得到它实际上等价于 (4) 用分离变量法,令u=f(φ)g(θ),由式(3)及(4)得 g″(θ)+c2g(θ)=0 g(j)(0)=g(j)(2π),j=0,1 (5) (6) f′(ξ)-σf(ξ)=f′(η)+σf(η)=0 (7) 式(5)的解显然是清楚的,考虑式(6)(7)。对于经典的Sturm-Liouville方程,特征值可以用Rayleigh商表达出来,因此需要将式(6)作变换,使它呈经典的Sturm-Liouville方程形式。 引理1 对于形如 y″+py′+qy+λy=0,y(0)=y(1) 的方程,若p∈L[0,1],则可以通过适当变换将其变换为经典的Sturm-Liouville方程的形式,即形如DpDy+qy+λy=0,y(0)=y(l)的方程。 证明作变换: f(0)=f(l)=0 可得证。 根据引理1,可以将式(6)变为想要的形式。作变换: h(x)=f(φ) 则有 (8) sinξh′(0)-σh(0)=sinηh′(A)+σh(A)=0 (9) 由Courant节点域定理不难得到当c2=0时,对应的式(6)(7)的最小特征值是式(3)的第一特征值,即 σsinξh2(0)+σsinηh2(A)} H(ξ)= 因此有λ1≤H(ξ),H(a)=λ1(a)。猜想当Ω关于赤道对称的时候,λ1达到最大值。为了得到这个结果,比较直观的想法是比较H(ξ)和H(a)的关系。于是便有下述定理: 定理1 式(3)中,若Ω面积固定为2πA不变,当Ω关于赤道对称时,λ1最大。 证明只需证明H′(ξ)>0,∀ξ∈(0,a)即可。这样便有 λ1≤H(ξ) 事实上, 而∀ξ∈(0,a),cotξ+cotη>0, 于是 证毕。 引理3 考虑 {p(x;t)y′(x;t)}′+λy(x;t)=0,x∈(0,1) y′(0;t)-h1(t)y(0;t)=y′(1;t)+h2(t)y(1;t)=0 其中t∈[0,1]为参数,p(x;t),h1(t),h2(t)≥a>0,且p(x;t)一阶偏导都连续,h1(t),h2(t)为光滑函数,则它的特征值关于t连续(如果没有特别说明,求导默认对x求导)。 证明利用最大-最小原理,类似于文献[6]定理6.10可证。 引理4 设u(x;t)满足: {p(x;t)y′(x;t)}′+λy(x;t)=0,x∈(0,1) y′(0;t)=h1(t);y(0;t)=1 若引理3中的条件成立,则u(x;t),u′(x;t)连续。 证明利用常数变易法,设 是该问题对应的齐次方程的两个解。 不难得到 (10) 由边条件有 c1(t)=u(0;t)=1 c2(t)=u′(0;t)p(0;t)=h1(t)p(0;t) (11) 由引理3和式(10)(11),逐次迭代可得证。 从而 σ(sin(ξ+Δξ)-sinξ)hξ+Δξ2(0)+ σ(sin(η+Δη)-sinη)hξ+Δξ2(A)≤ λ1(ξ+Δξ)-λ1(ξ)≤ σ(sin(ξ+Δξ)-sinξ)hξ2(0)+ σ(sin(η+Δη)-sinη)hξ2(A) (12) 由引理4及式(12),容易得到 则有 (13) 就能得到矛盾。事实上,如果式(13)成立,则有 λ1(a)≤H0(a) 这与定理1矛盾。 cosξcosφξ-sin2ξ=cosξ(cosξ-x)-sin2ξ cos2ξ-sin2ξ<0,∀ξ∈(ξ0,a) 最后,考虑sinξcotη,有 由引理2,得 证毕。 下面说明式(1)(2)中当Ω为高维(维度n≥3)空间中的球带时,它的第一特征值关于ξ也具有单调性。Rn中球坐标变换: x1=rcosφ1,…,xn=rsinφ1…sinφn-1 其中0≤φ1,…,φn-2≤π,0≤φn-1≤2π,称φn-2为最后一个天顶角;设Ω={x:0 (1)在球坐标系下的方程为 设u=h1(φ1)…hn-1(φn-1),则有 (14) … hn-k(An-k)=hn-k(Bn-k)=0 (15) … h1(A1)=h1(B1)=0 (16) 其中λ=sn-2,由Courant节点定理,当式(14)(15)中的每一个sk-1(k=1,2,…,n-2)都取对应方程的最小特征值(记作μk-1,且μ0=0)的时候,代入式(16),求得的最小特征值μn-2即为式(1)(2)的第一特征值λ1。 设Ω的面积为 2πSn-2…S1 由引理1,令 则式(19)变为 gn-k(0)=gn-k(Sn-k)=0,k=2,…,n-1 于是, (17) 证明由式(17)知道,μk-1(k=2,…,n-1)实际上是ξ的函数,记为μk-1(ξ),将μ0=0代入式(15)(取k=2),得 hn-2(ξ)=hn-2(η)=0 (18) (19) 由于μm-1(ξ1)=μm-1(ξ2)及式(17),∀ε>0,∃gε∈Tm,使得 又因为 于是 于是 这与式(19)矛盾。从而得到λ1=μn-2关于ξ严格单调增。证毕。 参考文献(References): [1] SINGER I M,WONG B,YAU S T,et al.An Estimate of the Gap of the First Two Eigenvalues in the Schroedinger Operator[J].Annali della Scuola Normale Superiore di Pisa-Classe di Scienze,1985,12(2):319—333 [2] SHEN C L,SHIEH C T.Some Properties of the First Eigenvalue of the Laplace Operator on the Spherical Bands[J].SIAM Journal on Mathematical Analysis,1992,23(5):1305—1308 [3] SHIEH C T.On the Second Eigenvalue of the Laplace Operator on A Spherical Bands[J].Proceedings of the American Mathematical Society,2004,132(1):157—164 [4] RAMM A G,SHIVAKUMAR P N.Inequalities for the Minimal Eigenvalue of the Laplacian in an Annulus[J].Math Inequalities and Appl,1998,1(4):559—563 [5] SHIEH C T.On the Behavior of the First Eigenvalue of the Sphereical Laplacian Operator on a Sphereical Annulus[J].Math Inequalities and Appl,2006,9(1):147—15 [6] COURANT R,HILBERT D.Methods of Mathematical Physics[M].NewYork:John Wiley & Sons,1989 [7] 刘景麟.常微分算子谱论[M].北京:科学出版社,2009 LIU J L.Spectral Theory of Ordinary Differential Operators[M].Beijing:Science Press,2009(in Chinese) [8] KONG Q,ZETTL A.Dependence of Eigenvalues of Sturm-Liouville Problems on the Boundary[J].Journal of Differential Equations,1996,126(2):389—407 [9] DAUGE M,HELGGER B.Eigenvalues VariationI.Neumann Problem for Sturm-Liouville Operators[J].J Diff Equations,1993,104:243—262 [10] 陈淼,杜厚维,向长林.一类分数阶Laplace算子方程解的正则性[J].长江大学学报(自然科学版),2020,17(6):108—113 CHEN M, DU H W, XIANG C L.Regularity of Solutions for a Class of Fractional Laplace Operator Equations[J].Journal of Yangtze University(Natural Science Edition), 2020,17(6):108—113(in Chinese)
1 主要结果和证明





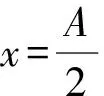
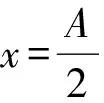
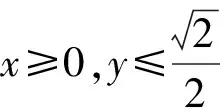
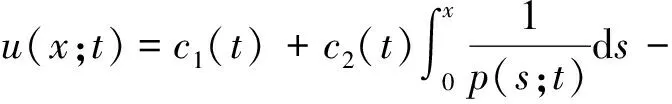
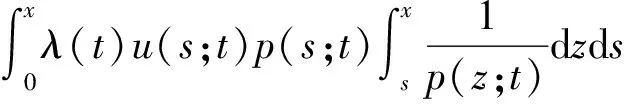





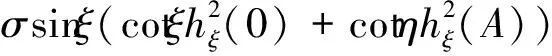
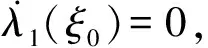
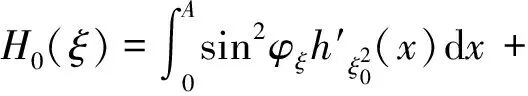
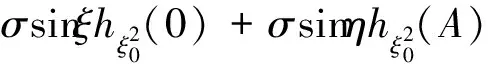

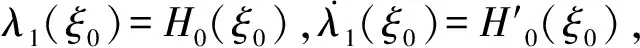
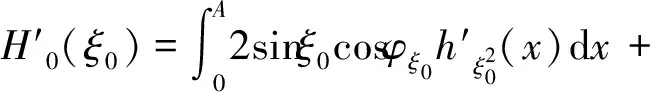
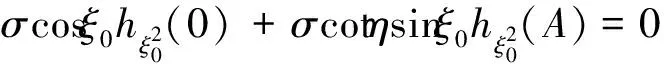
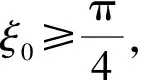


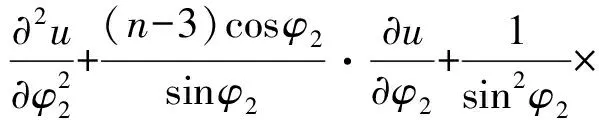

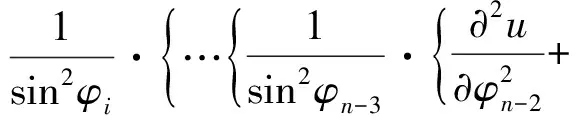


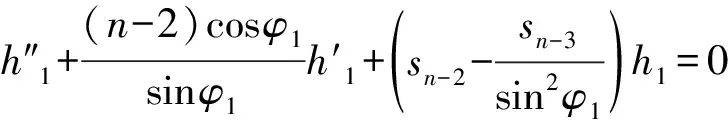
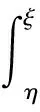
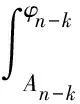
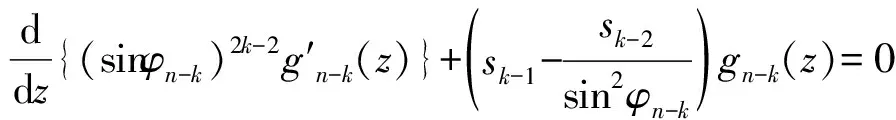

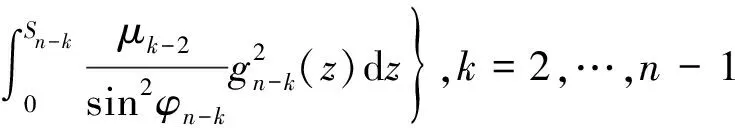

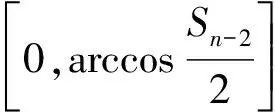
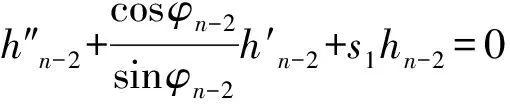
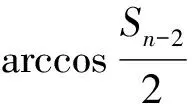
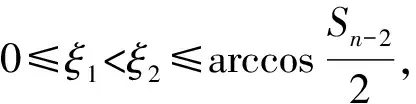
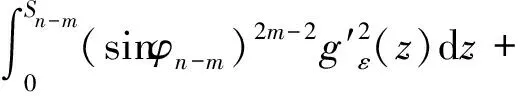
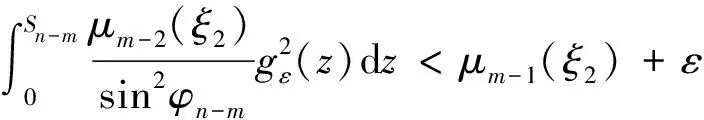



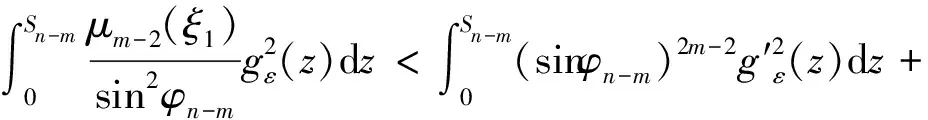
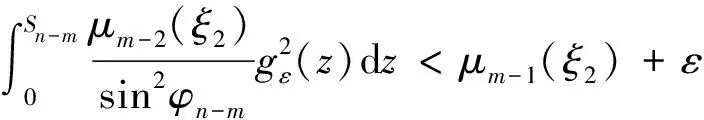
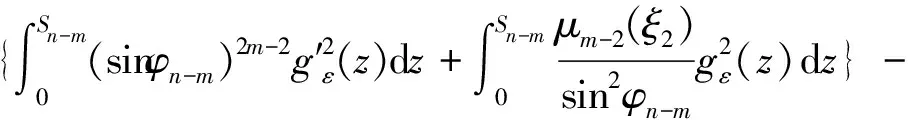

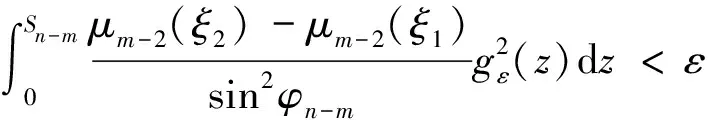
2 结束语