青藏铁路玉珠峰站半焊联无缝道岔稳定性分析

芦金新，牟 航，甘海云，李 媛，梁 涛

(1.中国铁路青藏集团有限公司 格尔木工务段，青海 格尔木 816099；2.兰州交通大学 土木工程学院，甘肃 兰州 730070)

无缝线路以长钢轨焊接取代钢轨的普通接头，已成为中国铁路正线的主要结构形式，具有增加行车平稳性、改善线路质量，节省接头材料、减缓线路变形累积，减少维修工作量、降低维修费用，延长线路设备和机车车辆使用寿命等优点，在世界各国都得到了广泛应用[1]，而作为实现跨区间无缝线路的重要环节，无缝道岔对于其设计、铺设与养护维修等问题的研究也愈发凸显出其重要性及必要性。

无缝道岔的稳定性分析问题得到国内外学者的广泛关注。国内李秋义、陈秀芳、娄平等人在解析模型的基础上，针对不同波长、不同轨道原始弯曲、不同道床横向阻力及轨温变化幅度等因素对无缝线路稳定性带来的随机影响展开研究，建立极值概率模型，并据此分析不同参数取值下无缝线路的稳定性，对稳定性可靠度进行随机模拟，得出不同边界条件对计算结果的影响程度[2-6]。中国铁路工务部门多用“统一公式”进行无缝线路稳定性检算，计算结果稳定可靠[7]。美国的W.So和G.C.Martin等人在1976年首次提出利用有限元模型进行稳定性分析，并建立世界上第1个无缝线路稳定性有限元模型[8]。2003年曾志平博士将轨枕视为弹性地基上的有限长梁，用基于弹性理论的戈氏法对其进行受力分析[9-10]。2001年西南交通大学王平教授在总结各种理论的基础上，基于有限单元法的思想，应用有限元法计算无缝道岔的温度力与位移[11-12]。2006年易锦利用基于变分原理的有限单元法建立无缝道岔的计算模型，分析无缝道岔纵向温度附加力与位移，并与有砟道岔进行对比，得到一些对工程实际有用的结论[13]。牟航等[14-15]运用有限单元法分析竖向沉降对无缝线路长钢轨温度应力的影响程度；周海宇等[16]研究轨道横向及复合不平顺对无缝线路稳定性影响分析。国内外关于无缝道岔的计算理论可以说各有所长，各研究成果均已得到实际工程的验证，表明研究结论正确。但有关空间体系下的无缝道岔稳定性分析鲜有文献报道，而青藏铁路格拉段多年冻土区易发生路基沉降等病害，需考虑线路前后高低等轨道病害对无缝道岔稳定性的影响。本文依托青藏线格拉段玉珠峰车站，针对无缝道岔结构建立空间杆件非线性有限元计算模型，结合实际位移观测数据，分析无缝道岔稳定性问题，为高原铁路铺设无缝道岔及养护维修研究提供理论依据。

1 无缝道岔模型的建立

1.1 力学模型

本文基于小变形假设，将轨道框架看作铺设在均匀介质中的细长压杆，建立12号固定辙叉无缝道岔三维模型。轨道框架模型采用60 kg /m 钢轨，弹条Ⅱ型扣件，混凝土Ⅱ型轨枕，每千米铺设轨枕1 760，从岔头向岔尾数，共计82个岔枕，道床肩宽为450 mm。道床横向阻力刚度为1 500 N/mm、道床纵向阻力刚度为2 500 N/mm、竖向的刚度为3 200 N/mm。单侧每段钢轨梁单元之间为刚性连接，用具有12个自由度的非线性梁单元代表钢轨，单侧每段钢轨梁单元之间为刚性连接，并且将首末两端钢轨单元的端点节点视为固定端约束；采用双结点弹簧单元来模拟连接钢轨与轨枕的扣件，扣件对钢轨的约束为弹性约束，将其视为无长度无质量的弹簧单元；不考虑道床抵抗轨枕扭转的作用。

在尖轨跟端处设置1对限位量为+8 mm、-6 mm的限位器，通过计算基本轨与导轨在尖轨跟端处的相对位移，得到限位器字母块紧贴时的温升值。在限位器字母块紧贴后，其作用力与随温升的关系，参照文献[17]选为14 kN/℃，并以1对节点力的形式加入到模型中。

1.2 非线性有限元的求解方法

基于Kirchhoff 假定，空间梁单元等截面梁单元应变由线性应变和非线性应变两大类组成[16]。在求解非线性问题时，用单元切线刚度矩阵来表达荷载与非线性位移的关系。

非线性有限元问题采用牛顿-拉斐逊方法求解，其迭代公式为：

1)量测线路不平顺，根据实测为初始位移赋值；

2)按线性分析得到节点位移的初值{δ}1；

3)在局部坐标系下构建单元切线刚度矩阵[KT]，并计算单元节点力[F]e；

4)将[KT] 和 [F]e转换至整体坐标系；

5)对所有单元重复3)和4)步骤，生成整体切线刚度矩阵[Kp]1及节点力向量[F]1；

6)计算不平衡力

{P1}={F}1-∑{F}e;

(1)

7)求解结构刚度矩阵方程2)，得到节点的位移增量Δ{δ}1

[KP]1·Δ{δ}1={P}1;

(2)

8)将Δ{δ}1叠加到结构位移向量{δ}1中，即

{δ}2={δ}1+Δ{δ}1;

(3)

9)收敛条件判断，若不满意则返回步骤3)。

(4)

式中:e为收敛精度。

2 焊联方案

对接接头是将2块钢板的边缘相对配置，并使其表面成一直线而结合的接头。这种接头能承受较大的静力和震动载荷，是焊接结构中最常用的接头形式。无缝道岔是将道岔内所有钢轨接头都消除的1种特殊道岔形式，钢轨接头连接有胶结接头和冻结接头两种方式，现场试验与应用实际均证明冻结接头在许多方面都优于胶结接头，并用50T拉压机对接头进行抗拉强度检测。在道岔直股采用冻结接头的形式来实现半焊联无缝道岔，侧股不焊，保持线路原有状态；利用冻结接头可提高夹板与钢轨上下颏接触面间的抗剪强度与摩擦力，使之不能相互滑移或适度控制滑移，以达到增强接头整体性和提高抗弯性的目的。现场冻结接头位置及位移观测桩位置如图1所示。

图1 现场冻结接头位置及位移观测桩位置

3 温度变化对位移的影响

无缝道岔内部存在着极为复杂的传力关系，加之轨温变化以及线路存在的不良情况，将对无缝道岔的受力变形产生极大的影响。高原铁路昼夜温差大导致道岔温度内力变化大，有砟轨道横向稳定性较差，基于建立的轨道框架模型计算分析，将无缝道岔整体结构依次升温0 ℃、10 ℃、20 ℃、30 ℃；整体结构依次降温0 ℃、-10 ℃、-20 ℃、-30 ℃、-40 ℃，求解其横向位移及纵向位移随温度改变的变化规律。

无缝道岔升温时各轨线变化趋势相近，横向位移的方向以从岔首朝向岔尾，左侧为正，右侧为负。直基本轨的受力特征较为明显，在不同温升条件下，其横向位移变化趋势如图2所示，各不利位置岔枕如图3所示，直基本轨不利位置点横向位移峰值见表1。从模型计算结果可看出无缝道岔在直基本轨转辙部分6号岔枕、21号岔枕、导曲线部分41号岔枕、辙岔部分57号岔枕、74号岔枕处产生外侧横向位移峰值，在辙岔部分63号岔枕、77号岔枕产生里侧的横向位移峰值，最大横向位移变化由岔心至翼轨末端，即63号岔枕处，升温30 ℃时，其横向位移大致为0.651 9 mm；75号岔枕处有断开，位移在74号岔枕处产生峰值，随后急剧减小。由温升条件可知，温度越高钢轨产生横向位移越大，升温30℃较升温0℃位移最大增加约90.7%，最小增量为64.8%。降温时变化规律与升温时正好相反，不同温降条件下，其横向位移变化趋势如图4所示。

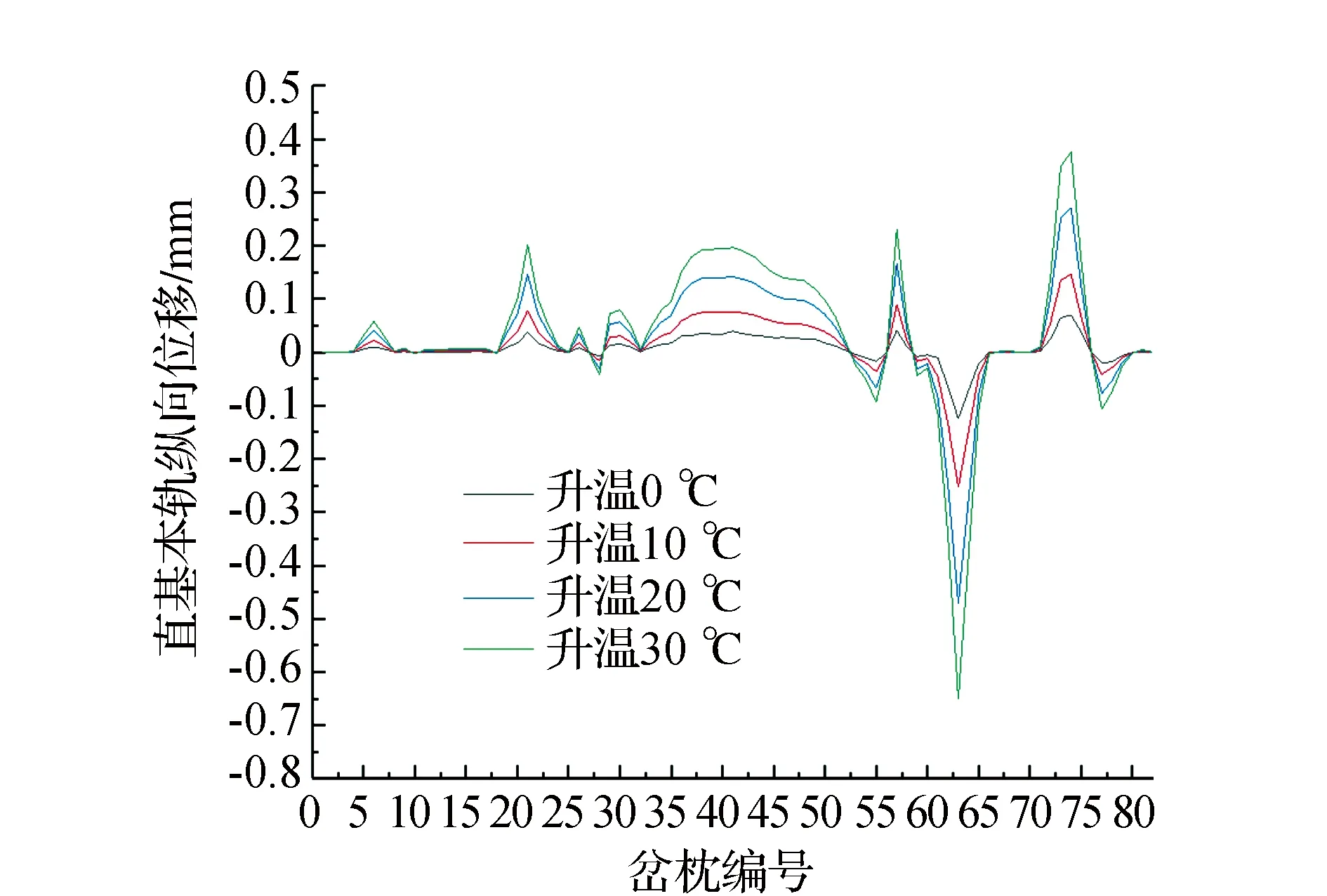
图2 岔区升温条件下钢轨位移计算

图3 各不利位置岔枕

图4 岔区降温条件下钢轨位移计算

图5 不同温升条件下曲尖轨纵向位移

图5为不同温升条件下，曲尖轨产生的纵向位移，选取部分岔枕进行分析。规定道岔内部各轨线由岔尾向岔首爬行，纵向位移为正。通过计算结果可知，随着温度的升高，曲尖轨产生纵向位移不断增大。当升温30 ℃时，尖轨跟端处限位器作用力为36.9 kN，曲尖轨尖端(6号岔枕)产生最大纵向位移，位移值为10.561 6 mm。

图6所示为升温30 ℃时，无缝道岔各轨线产生的纵向位移。直基本轨与曲基本轨在尖轨跟端(24岔枕)处产生纵向位移峰值分别为1.791 3 mm，1.814 2 mm。

图6 升温30 ℃时各轨线纵向位移

曲导轨与直导轨在尖轨跟端(24号岔枕)处产生纵向位移分别为5.979 1 mm及5.861 9 mm，由尖轨跟端向后至辙岔处纵向位移不断减小，由于翼轨末端自由伸缩，使得纵向位移变为负值即向岔尾移动。升温30 ℃时，间隔铁阻力为87 kN,由于心轨尖端自由伸缩，长心轨在58岔枕处产生最大纵向位移分别为4.029 mm，纵向位移向岔尾处不断降低。

根据现场实测数据(见表1),玉珠峰站年施工锁定轨温为16.8 ℃(设计锁定轨温(14±5)℃)，年最高轨温为26.8 ℃，温升幅度为10 ℃时，由图5可知，在曲尖轨跟端产生最大纵向位移，大致为3.52 mm。现场位移观测桩实测数据如表2所示。玉珠峰站8月份年轨温达到最大值，表2中道岔尖轨跟端处纵向位移左股为-5 mm，右股为-4 mm；模型计算出来的数据结果正确，与现场实测数据相符。

表1 直基本轨不利位置点横向位移峰值 mm

表2 现场实测数据 mm

4 应变分析

本文采用应变法来测试轨温变化下的钢轨应变增量值，温度变化会影响应变计本身的传感特性，应变计种类虽多，但是电阻应变片与振弦式传感器在钢轨、桥梁检测中是最常用的，由文献[18]得出，温度会对应变仪测试的电阻产生较大影响，从而影响测试结果，但温度对于振弦式传感器的影响是可以忽略的。与其他传感器相比，振弦式应变传感器具有测量精度高、读数稳定、使用方便等优点[20]，应用在船舶下水试航、大坝初次蓄水监测及其长期监测、桥梁工程的验收、荷载试验及施工控制等。本文选择振弦式应变片进行测试。

采用应变电测法监测无缝线路实际锁定轨温的变化，测量玉珠峰车站道岔产生的应力、应变与轨温变化的关系。由于高原高海拔地区日温差变化较大，选择钢轨应变发展较为稳定的晴天，连续观测24 h，每2 h读取传感器的温度和应变值，观测在温度变化条件下无荷载变化时振弦式应变传感器本身的应变变化特性。为确保岔区半焊联锁定后，长钢轨应力状态满足低温抗拉、高温抗压的使用要求，保证线路运营安全，项目组分2次布设钢轨应变检测点，检测点分别布设在正线直股道、导曲线后部左直股和导曲线中部左直股上，检测了轨温循环变化条件下钢轨应变增量值。

在自由状态下钢轨、正线区钢轨以及岔区钢轨处安装钢轨表面ZX-212CT振弦式应变计。振弦式应变传感器的量程为±1 500×10-6，温度测量范围为-20～125 ℃。

振弦式应变计和振弦式测试仪见图7。本次采用的振弦式应变计可以同时测量温度和应变[21]，温度和应变的测量精度分别为0.1 ℃和0.1×10-6。

图7 振弦式应变测试仪(a)及应变计(b)

岔区直股道与正线应变增量对比分析见图8，测点1、2位于正线直股道，测点3、4分别位于导曲线后部左直股和导曲线中部左直股。钢轨应变观测初始轨温为21.8 ℃，轨温升高，钢轨受压，应变增量为正值，轨温降低，钢轨受拉，应变增量值为负值。钢轨应变增量值与轨温变化幅度相关，轨温变化越大，钢轨应变增量值越大。当钢轨从最高轨温27.6 ℃下降到24.3 ℃时，受辙叉处轨线断开的影响，导曲中、后部直股应变增量略小于正线直股，随着轨温继续下降，导曲线中、后部钢轨应变增量与正线规律基本一致。

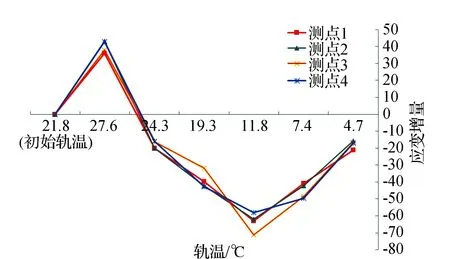
图8 岔区直股道与正线应变增量对比分析

5 结 论

1)根据岔区与正线长钢轨应变增量变化规律、位移观测数据以及模型计算结果，经综合分析可以发现玉珠峰车站岔区半焊联无缝道岔方案可行，岔区长钢轨在温度应力作用下稳定。

2)玉珠峰车站年平均气温较低，但由于车站海拔高，轨温易受气候影响产生较大幅度的波动变化，在线路运营过程中，需加强岔区长钢轨位移观测。