轴向柱塞马达平面配流副油膜润滑特性建模及分析

侯亮 赖伟群 崔凯 叶绍干† 郭志敏 卜祥建

(1．厦门大学 机电工程系，福建 厦门 361021；2.林德液压(中国)有限公司，山东 潍坊 261061)

轴向柱塞泵/马达紧凑高效、排量可调，广泛应用于建筑机械、矿山机械、航空航海等重大装备的液压系统[1- 5]。配流副作为柱塞泵/马达三大摩擦副之一，在工作过程中容易出现早期磨损，对泵/马达的压力等级、转速工况及寿命具有直接影响[6- 9]。配流副端面之间须形成适当厚度的润滑油膜，以保证配合端面之间的充分润滑,避免油膜过薄或过厚导致的“烧盘”或泄漏量过大现象[10- 13]。配流副润滑特性对轴向柱塞泵/马达的容积效率与工作寿命有重要的影响[14- 16]。

国内外学者均对轴向柱塞泵进行了大量的研究，Huang等[17]针对配流副油膜流场提出了一种关于配流副承载能力的数值分析方法。Bergada等[18]通过配流副油膜润滑状态观测，发现缸体与配流盘之间存在混合润滑状态，强调了弹性变形在缸体动力学分析中的重要性。Zecchi等[19- 20]在考虑油液黏滞、弹性变形以及热变形等条件下建立了配流副CASPAR模型，探究了配流副的摩擦润滑、泄漏以及温度场等特性。国外研究表明配流副油膜润滑特性影响因素众多，基于理想配流端面的配流副刚体模型进行分析准确度有限，适用范围具有局限性。张浩等[21]基于CFD仿真对柱塞泵进行流场分析，获得了柱塞泵油膜的压力分布及柱塞腔内压力变化曲线。王震等[22]对摩擦副间隙进行研究，运用Pumplinx建立空化模型，分析不同配流盘减振结构下的流量和压力脉动。赵愿等[23]针对配流副磨损问题建立开槽配流端面动压支撑特性数学模型，分析开槽端面油膜动压分布及支撑作用。钱文鑫等[24]基于AMESim分析了柱塞数、转速及斜盘倾角对流量脉动的影响。以上研究主要针对轴向柱塞泵模型，在轴向柱塞马达配流副方面的研究相对较少，且现有研究未考虑表面纹理及辅助支撑带对油膜压力分布与力矩的影响。

本研究针对柱塞马达配流副油膜润滑特性,在考虑油膜流体径向惯性力的条件下，运用有限容积法进行数值建模，同时考虑表面纹理及辅助支撑带对压力场与力矩的影响，对比工作压力、转速及斜盘倾角对轴向柱塞马达配流副摩擦润滑特性的影响，对配流副的摩擦泄漏、承载润滑等性能进行深入分析，以获得不同压力、转速和斜盘倾角下配流副泄漏以及摩擦转矩的变化规律。

1 配流副模型

1.1 配流副端面几何结构

配流副为配流盘与缸体的配流端面组成的摩擦副。其配流端面几何结构如图1所示，缸体配合端面主要由腰形槽、内/外密封带组成；配流盘配合端面主要由高/低压腰形槽、内/外密封带、辅助支撑带及阻尼槽组成。其中，ω为缸体转速，R1、R2分别为内密封带内外径，R3、R4分别为外密封带内外径，R5、R6分别为辅助支撑带内外径，Rc为柱塞圆心分度圆直径，θhs为高压区腰型槽起点张角，θhe为高压区腰形槽终点张角，θls为低压区腰型槽起点张角，θle为低压区腰形槽终点张角，各结构参数如表1所示。由于缸体相对于配流盘旋转具有周期性，故配流副各点油膜厚度也随着缸体转动变化而呈现周期性变化。

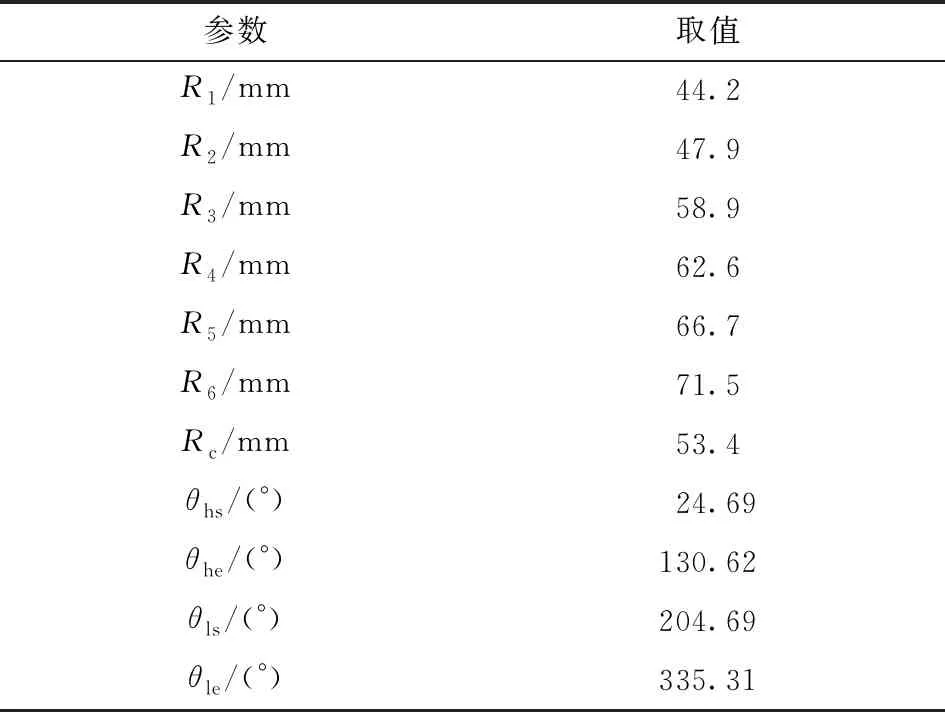
表1 配流副端面几何结构尺寸参数

1.2 缸体动力学模型

图2为缸体与柱塞滑靴组件受力分布图。缸体主要受到两部分力，一个是配流副油膜缸体的支承力及力矩，另一个是柱塞/滑靴组件及中心弹簧引起的压紧力及力矩，缸体共受到9组柱塞滑靴组件的压紧力及力矩作用。

如图2所示，Bi和Ci分别为柱塞滑靴组件的滑靴球心与质心，沿轴向方向，缸体受柱塞腔油液压力ppK、中心弹簧压紧力FS、油膜压力poK及柱塞腔摩擦力FT作用，而相比柱塞腔油液压力，摩擦力大小可忽略不计。而沿x、y轴方向，缸体受到由油膜压力poK、柱塞腔油液压力ppK、柱塞滑靴组件径向惯性力Fω以及斜盘支撑力FN引起的合力矩Mx、My。图2中ppBi表示柱塞腔内油液对柱塞的压力,在动平衡状态下，缸体平衡方程为：

(1)

1.3 油膜流体润滑模型

为分析柱塞马达配流副油膜压力分布，建立配流副油膜流体润滑模型。根据配流副间隙相对配流盘尺寸极小，可认为油液在间隙内流动特性为层流，故对模型作以下假设：①配流副间隙油液流动特性为层流；②配流副油液为理想牛顿液体，油液密度不随压力及温度变化；③油液满足近壁面无滑移边界条件；④油膜厚度尺寸相对周向与径向尺寸极小，认为油膜压力沿膜厚方向不变。

根据以上假设，忽略重力影响，考虑流体径向惯性力，建立极坐标下的流体雷诺方程如式1所示。

(2)

式中,r、θ为油膜各点所在坐标,h、p分别为油膜厚度与压力,ω为缸体转动角速度,t为时间,vr、vθ为油膜沿径向与周向速度,ρ为油液密度,η为油液动力黏度。

由于式(1)所示雷诺方程为椭圆形偏微分方程，故运用控制容积法对该方程进行离散化，即将雷诺方程求解域划分成多个互不重叠的单元容积，并将方程在如图3所示求解域中进行数值离散。采用交错网格，图示白黑节点分别代表压力分布节点与速度分布节点。

图中，Δθ为单元容积的周向角度，ΔR为单元容积的径向长度。对应求解域边界条件如下：

(3)

式中:p0为泄漏边界压力，即为大气压;ph和pl分别为油液进口压力及出口压力。对式(2)在控制容积上积分可得

(4)

求解可得雷诺方程的离散形式为

aPpP=aWpW+aEpE+aSpS+aNpN+S

(5)

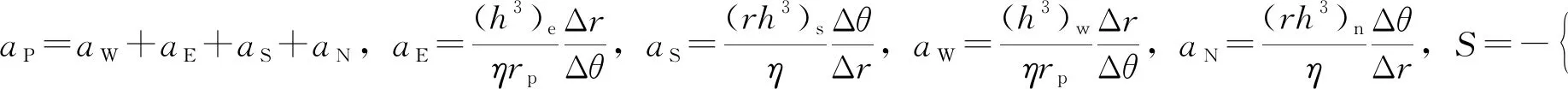
采用环形三对角阵算法(CTDMA算法)求解压力场边界上各节点压力值，进而沿径向对该油膜压力场进行迭代求解，获得配流副油膜压力分布。根据求得的压力分布，可得油膜支撑力及力矩如下：

(6)

1.4 配流盘表面纹理

受加工精度以及材料成型技术限制，实际配流盘表面并非完全平滑，而是具有一定的表面纹理，而表面纹理带来的不平整峰谷分布会引起流体动压效应，从而导致在峰谷处会产生一定的油膜支撑力。故本研究在分析配流副间隙油膜润滑特性过程中，同时考虑配流端面的表面纹理对油膜厚度的影响。本研究主要考虑配流盘的表面纹理，且假设柱塞马达配流盘表面纹理分别沿配流盘周向和径向呈现全正弦分布[21]。配流盘端面任一点(r,θ)的表面纹理高度Δh为

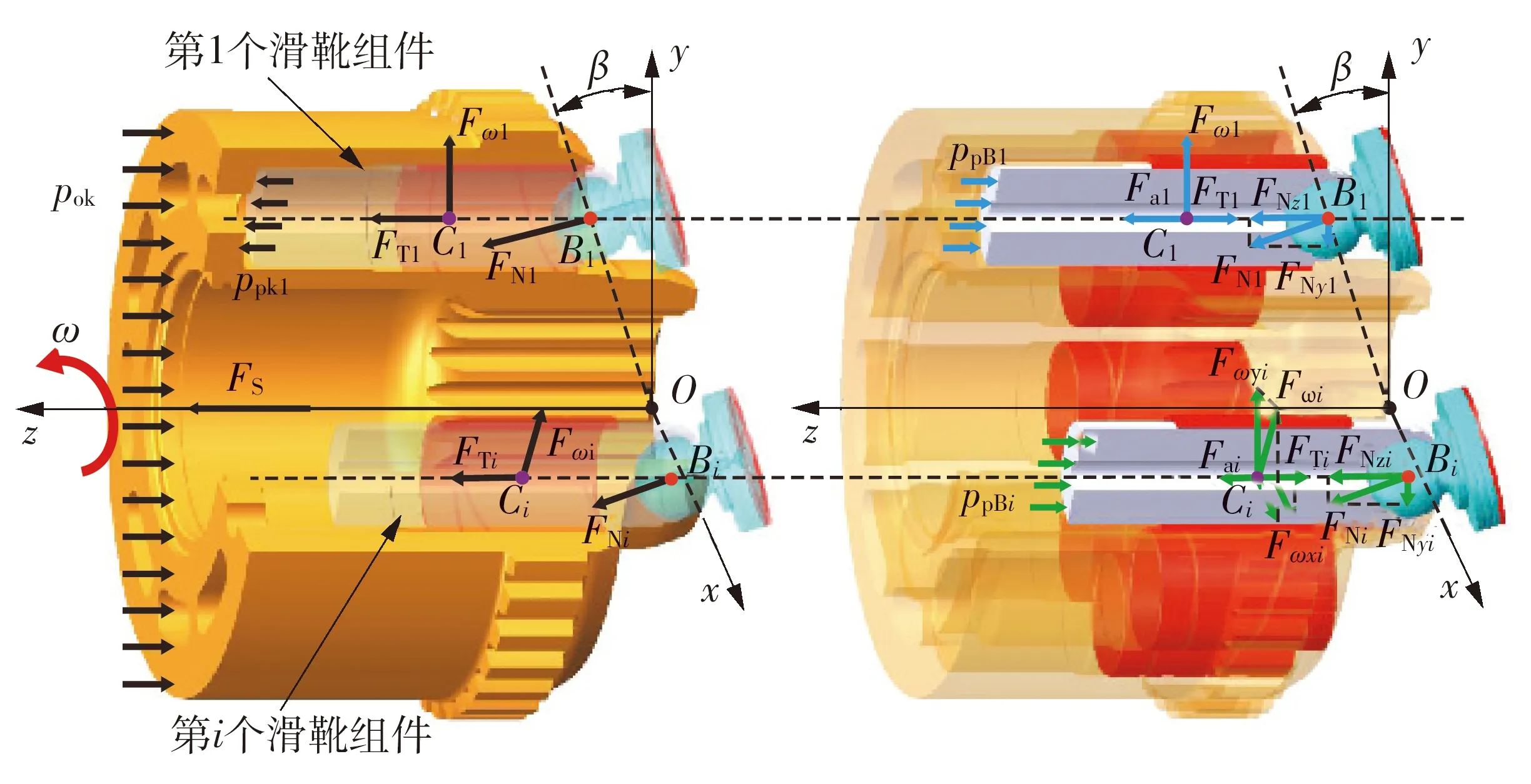
图2 缸体及柱塞滑靴-组件受力分析图

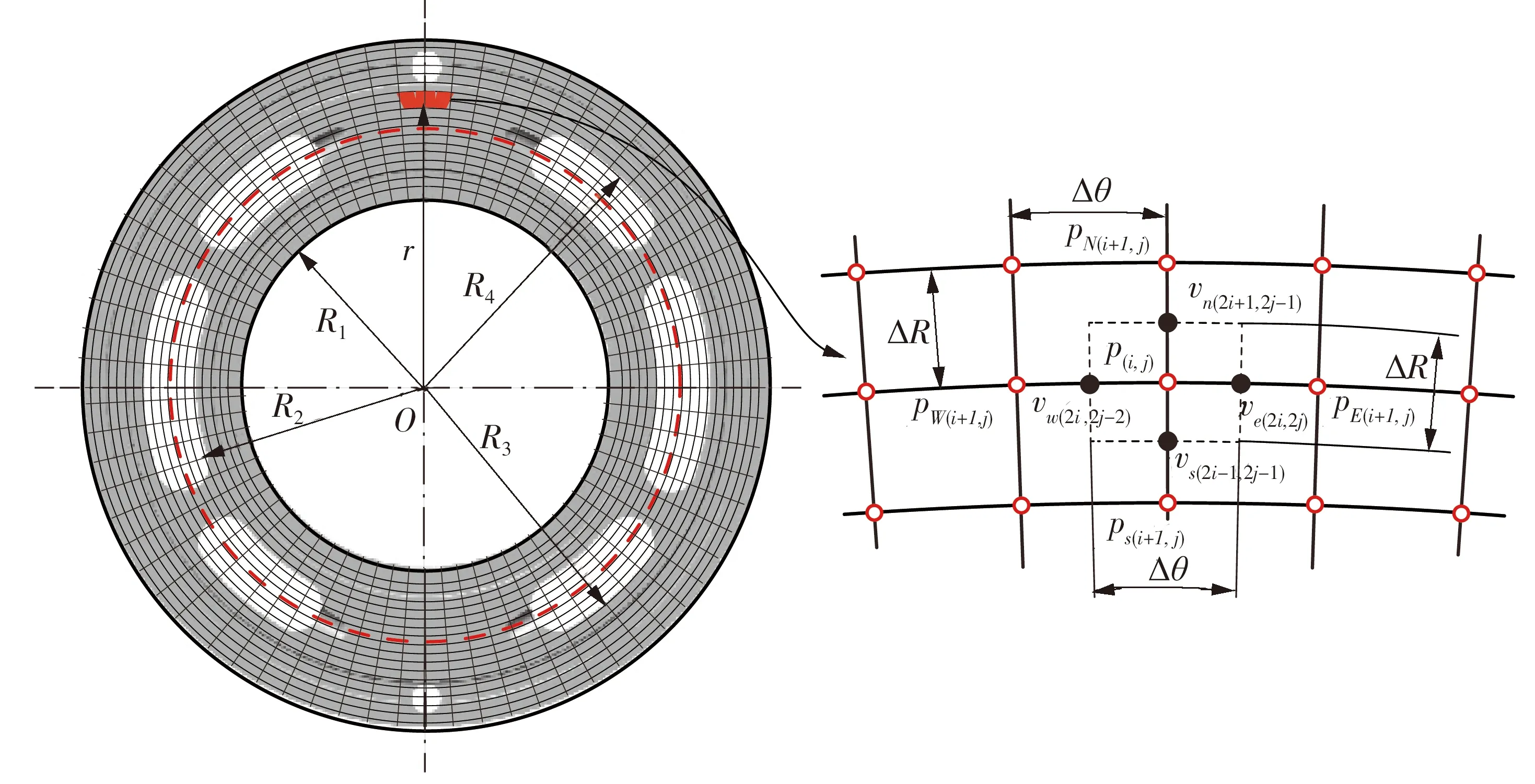
图3 方程求解域与控制容积示意图

(7)

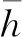
1.5 油膜泄漏流量模型

如图4所示，配流副泄漏主要为内泄漏与外泄漏之和，其中内泄漏为由缸体周向旋转，带动油液从缸体腰形槽流向邻近腰形槽引起的泄漏；外泄漏为由于压差作用，油液由配流副间隙流向壳体所引起的泄漏。

由于内泄漏相对外泄漏可忽略不计，本研究只针对外泄漏进行探析。根据配流副间隙油液压力场分布，可得油液径向速度场分布为

(8)

该式表明油膜径向流速受压差作用项及一次、二次转速项影响，其中z为油膜沿膜厚方向的高度。则通过对内外密封带边界油液速度场积分可得配流副油膜泄漏Q为

图4 配流副泄漏示意图

(9)

1.6 油膜摩擦转矩模型

由于配流副间隙油膜存在粘性摩擦力，并形成绕主轴轴线的粘性摩擦转矩，对缸体沿配流盘表面作旋转运动造成阻碍，同时油膜周向压差的作用也会造成柱塞马达的摩擦转矩损失。其摩擦转矩Mf为

(10)

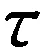
(11)

2 数值分析结果

文中给出压力工况为28、35、42、49 MPa，转速工况为1 500、1 600、1 700、1 800、1 900、2 000 r/min，配流副油膜仿真参数如表2所示。

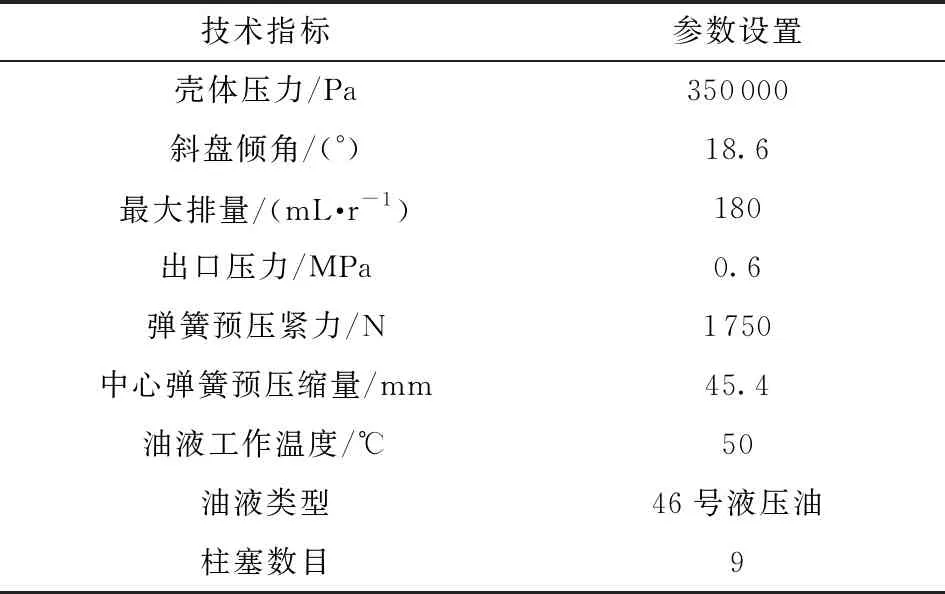
表2 配流副仿真参数

2.1 缸体倾覆力矩分析

柱塞马达配流副工作过程中，缸体受柱塞腔油液压力以及柱塞滑靴组件惯性力所产生的倾覆力矩作用，缸体分别有沿上死点以及高压区倾斜的倾向。图5示出了工作转速1 700 r/min、工作压力35 MPa、斜盘倾角18.6°下，缸体绕x轴和y轴的倾覆力矩Mx、My随方位角转动的变化曲线。图中φ表示方位角，指缸体绕主轴的旋转角度。

如图5所示，由于柱塞数目为9，受缸体旋转作用，绕x轴和y轴力矩均呈现40°周期，与柱塞角度间距一致。而由于缸体旋转，带动柱塞滑靴组件惯性力绕x、y轴力矩的作用力臂长度变化，同时带动柱塞腔内油液压力波动变化，在双重影响下，绕x、y轴力矩一个周期内均存在一大一小两个峰值。同时Mx、My幅值分别在18～112 N·m和3 144～3 165 N·m之间，可见Mx幅值远小于My，表明缸体受My作用远大于Mx，相比缸体受绕x轴力矩作用沿上死点倾斜，缸体更倾向于沿高压区中间位置倾斜。

图5 不同方位角下倾覆力矩

2.2 油膜厚度场

图6给出工作转速1 700 r/min，工作压力35 MPa，斜盘倾角18.6°下，马达工作稳定时，缸体旋转方位角分别为0°、10°、20°、30°、40°下的配流副油膜瞬时厚度场。由图6所示，在主轴旋转过程中，配流副油膜最小厚度位置位于高压区中心位置，表明缸体在旋转过程中有沿高压区中心倾斜的倾向，而缸体倾斜动作是由于旋转过程中受活塞滑靴组件径向惯性力以及受斜盘支撑力产生的倾覆力矩作用导致。结果表明了配流副油膜厚度场的非均匀性，反映出缸体在旋转过程中一般处于倾斜姿态，对高压区进行挤压，以产生油膜动压效应抵抗外负载。而最小油膜厚度位置变化受Mx、My变化影响，由图5所示，My变化较小，且远大于Mx，故在缸体旋转过程中，最小膜厚点始终在高压区配流窗口中心位置上下略微浮动。

2.3 油膜压力场

图7示出了考虑流体径向惯性力，工作转速1 700 r/min，工作压力35 MPa,斜盘倾角18.6°，马达工作稳定时多个方位角下配流副油膜的瞬时压力场。方位角为0°代表马达上死点位置。由图7可见，0°方位角下配流副油膜的瞬时压力场分布与40°方位角下压力分布相同，可知配流副油膜瞬时压力场随缸体转动呈40°周期变化。

由图7所示，从 0°转至20°方位角，初始位于上死点的柱塞由于缸体旋转，逐渐接入配流盘高压腰形槽，促使上死点区域压力上升，从而高压区域得到拓宽；而在柱塞旋出高压腰形槽后，该区域压力随之下降。图8给出了在0°方位角下配流副辅助支撑带的压力分布，可知支撑带油膜存在动压作用，最大压力位于高压区中心且稍微靠近上死点的位置，对应图6的油膜厚度分布结果，表明高压区中心位置油膜为受挤压严重区域；同时表面纹理所带来的流体动压效应导致支撑带压力场出现多个压力峰，压力分布由最大值沿两侧递减。

3 工况对泄漏的影响

配流副泄漏主要由内泄漏与外泄漏两部分组成，其总泄漏量可达到柱塞马达总泄漏量的50%～75%[10]。本研究选取不同工作压力、工作转速及斜盘倾角，针对柱塞马达配流副泄漏进行分析。

3.1 压力及转速对泄漏的影响

由泄漏流量理论模型中的式(8)、(9)可知，配流副泄漏流量与油膜沿径向方向流速呈正相关，而油膜径向流速与油膜压力、主轴转速相关。图9、图10为不同工作压力下配流副泄漏量、中心膜厚随转速变化曲线。

由泄漏量变化曲线可知，同一工作压力下，泄漏量基本随转速提升呈近线性增大，体现了泄漏模型式(8)中的一次转速项的作用。同时对比不同压力下泄漏量的增长趋势，发现泄漏量随转速提升的增长速率随着压力增大而降低，结合图10所示，油膜中心膜厚随工作压力增大而下降，表明式(8)中的一次、二次转速项对油膜径向流速的作用随着压力增大而减弱。同时受压差作用，同一转速下，泄漏量随压力增大呈上升趋势，而当随着压力增大，膜厚下降，故压差作用效果明显程度也随之下降。

图7 不同方位角配流副油膜压力分布

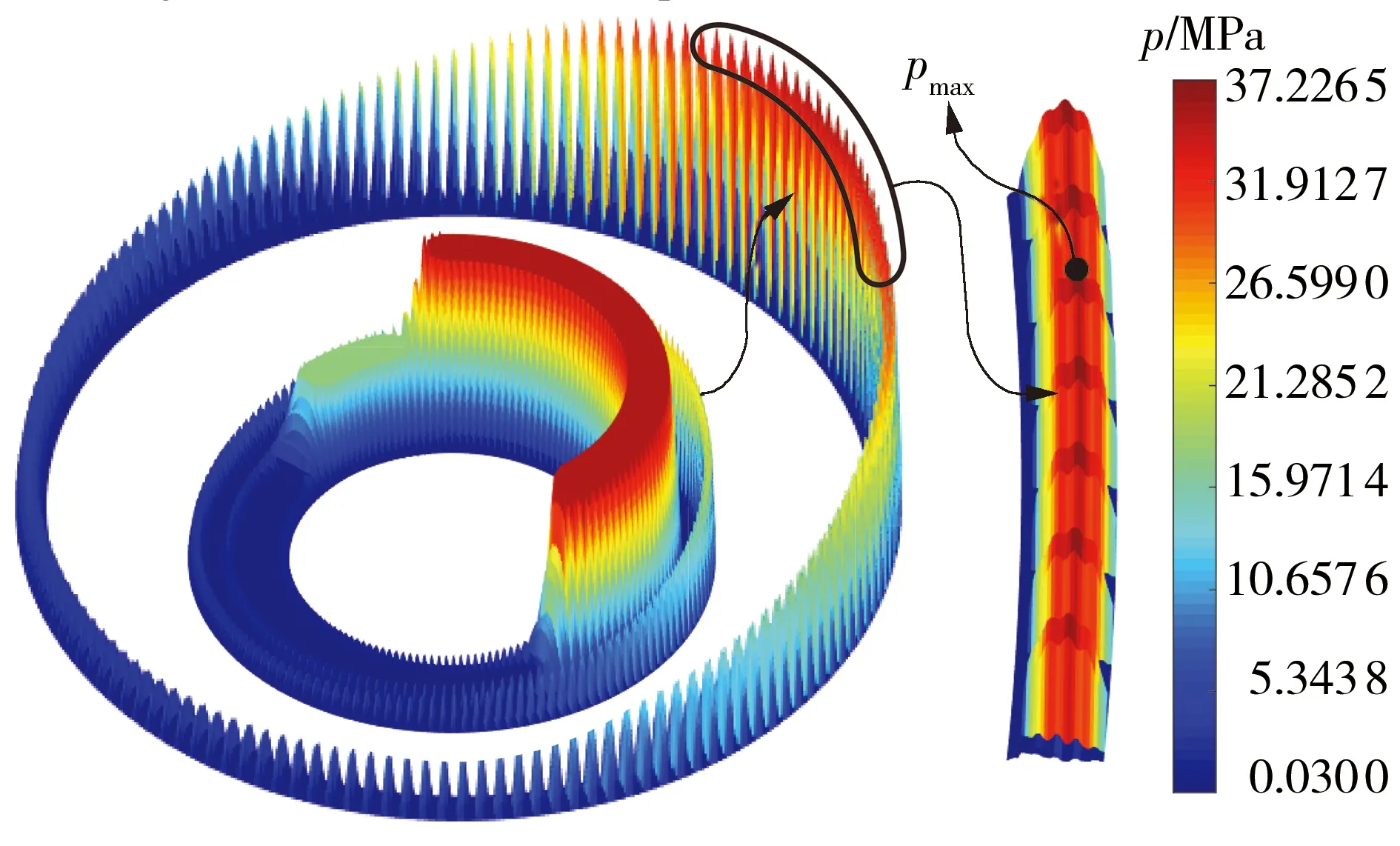
图8 辅助支撑带油膜压力分布

图9 不同工作压力下泄漏流量随转速变化

图10 不同工作压力下中心膜厚随转速变化

结果表明配流副泄漏流量与工作压力及转速密切相关，当转速提升、工作压力增大，均将促使油膜内油液径向流速增快，进而增大泄漏。

3.2 斜盘倾角对泄漏的影响

柱塞马达斜盘倾角γ直接决定柱塞马达排量V，同时影响缸体所受滑靴柱塞组件的倾覆力矩力臂长度，对配流副动力学特性具有影响，进而可能对配流副的泄漏具有一定影响。如式(12)所示，通过改变斜盘倾角可以实现对配流副排量的改变。

(12)

式中，dz为柱塞直径，z为柱塞数，D为柱塞所在分布圆半径。本研究选定工况转速1 700 r/min，工作压力35 MPa，选取斜盘倾角为12.6°、15.6°、18.6°、21.6°时进行对比分析，就斜盘倾角对配流副泄漏的影响进行探究。

图11示出了配流副中心膜厚及泄漏在不同斜盘倾角下的变化，当斜盘倾角增大，配流副中心膜厚及泄漏随之下降，表明配流副泄漏受斜盘倾角影响。一方面斜盘倾角增大，压紧力矩力臂长度增大，缸体受柱塞滑靴组件压紧力矩随之增大，导致缸体整体膜厚下降；一方面倾角增大，中心膜厚下降，配流副间隙整体油量减少，导致泄漏下降。

图11 不同斜盘倾角下中心膜厚及泄漏变化

4 工况对摩擦损失的影响

4.1 压力及转速对摩擦损失的影响

配流副摩擦损失主要来自配流副油膜粘性摩擦力矩作用和表面粗糙峰带来的固体摩擦力作用，本研究主要针对配流副油膜粘性摩擦力矩进行研究。图12示出了不同工作压力下配流副油膜粘性摩擦转矩随转速的变化曲线。

图12 不同工作压力下摩擦转矩随转速的变化

如图12所示，工作转速在1 500 r/min到2 000 r/min之间变化，在同一工作压力下，摩擦转矩随转速呈近似线性增大，且同一转速下，转矩亦随压力增加而增大。由式(10)、(11)可知，油膜粘性摩擦力矩与油液内切应力有关，而切应力受油液周向流速影响，且油液周向流速与主轴转速呈线性相关，故在全流体润滑状态下，摩擦转矩随主轴转速提升而呈现近似线性变化；同时由图10可知，工作压力提升将导致整体油膜厚度减小，进而增大油膜切应变率，最终使油膜摩擦力矩增大。

4.2 斜盘倾角对摩擦损失的影响

图13给出配流副中心膜厚及摩擦转矩在斜盘倾角分别为12.6°、15.6°、18.6°、21.6°时的变化曲线，当斜盘倾角增大，配流副中心膜厚有所降低，摩擦转矩随之增大。根据油膜摩擦转矩模型，可知油膜粘性摩擦转矩主要受油膜流速及膜厚等影响，结合仿真结果可知，斜盘倾角增大导致整体油膜厚度下降，进而增大油膜沿膜厚的切应变率，促使油膜粘性摩擦力矩增大。

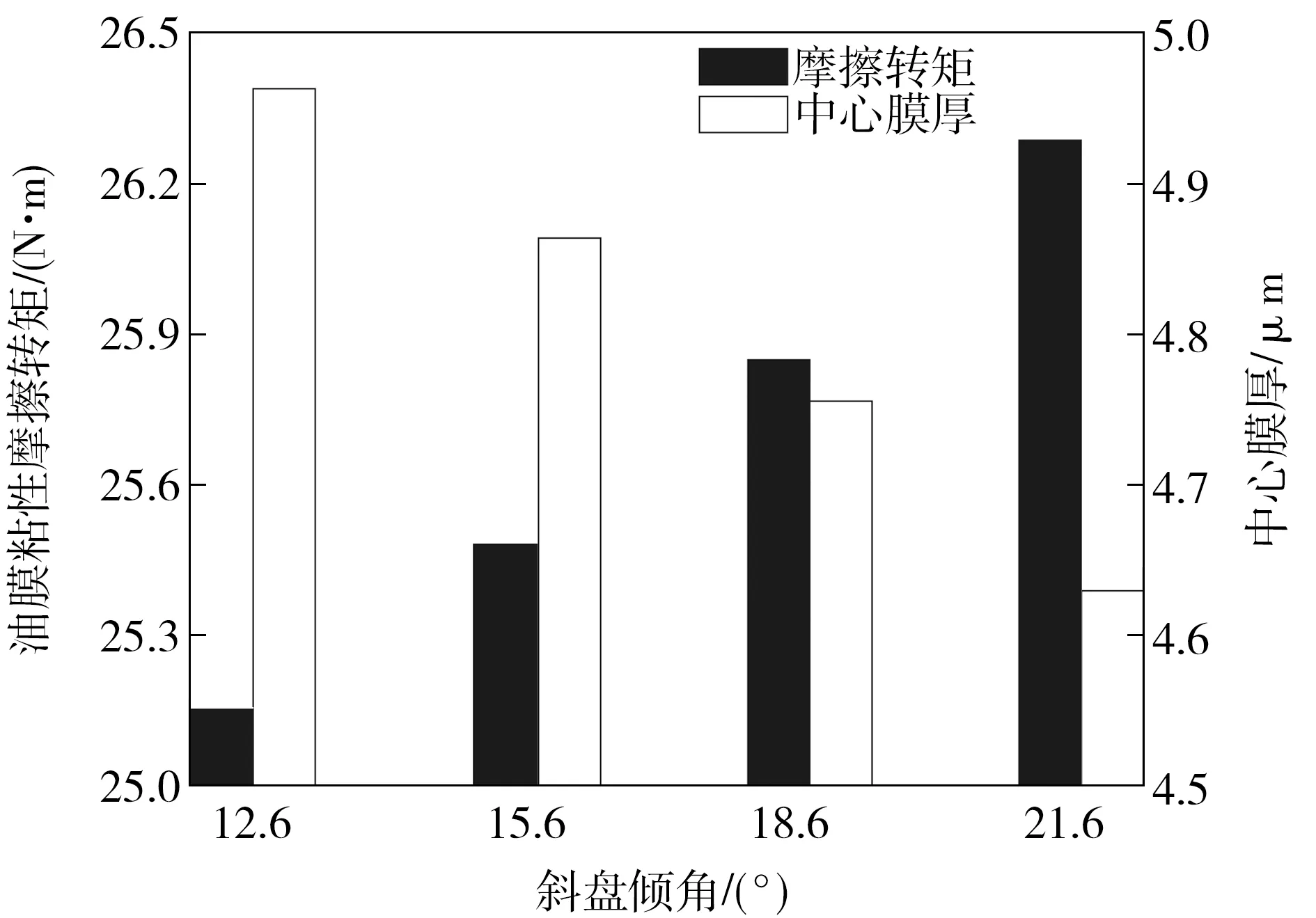
图13 不同斜盘倾角下中心膜厚及摩擦转矩变化

5 结论

本研究考虑柱塞马达配流盘表面纹理的影响，建立了包含辅助支撑带油膜压力分布与力矩作用的油膜润滑特性模型，探究了工作压力、工作转速以及斜盘倾角对配流副流量泄漏以及摩擦损耗的影响规律。

(1)柱塞马达配流副泄漏流量与马达工况相关，当转速、工作压力增大时，油液流速增大，泄漏量随转速提升呈近线性增长；而随着压力增大，膜厚不断下降，转速、压差对流速作用减弱，泄漏量随转速增大的增长速率有所下降。

(2)随转速、压力提升，油膜粘性摩擦力矩呈现增大趋势，摩擦力矩随转速提升呈近线性增长；而压力增大导致膜厚下降，结合摩擦转矩模型，油膜切应变率将增大，促使油膜摩擦力矩增大。

(3)配流副中心膜厚及泄漏流量随斜盘倾角增大呈现下降趋势，而摩擦转矩随斜盘倾角增大而增大，证明斜盘倾角虽未直接体现在泄漏流量模型与摩擦转矩模型中，但仍对配流副泄漏与摩擦特性有一定影响，且应存在较佳斜盘倾角角度，使配流副泄漏与摩擦转矩均取得较优的值。

(4)辅助支撑带压力分布表明，带表面纹理的辅助支撑带存在较大的压力峰值，在油膜承载中起到重要的作用，在油膜承载力的组成中应考虑其影响。此外，由于本研究假设配流副油液为理想牛顿液体，未建立温度场对油膜特性影响分析模型，因此可将其影响作为后续的一部分研究工作。