基于出行者稳定性的简化活动模型结构研究

陈先龙 陈小鸿

(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.广州市交通规划研究院信息模型所,广东 广州 510030)

交通模型作为基本工具和核心分析技术被广泛应用于交通规划、运行和管理决策，其精度和效率一直是交通模型工程师所关注和追求的关键指标。交通模型规划方法从早期的趋势预测法，到20世纪50年代的集计模型[1](四步骤交通模型理论为代表)，再发展到20世纪70年代的非集计模型[2](基于活动的出行需求模型(ABM))。从国内外实践经验来看，虽然四步骤模型有着多种缺陷[3]，但目前仍然是使用最广泛的交通规划模型,且从模型结构到各个步骤等的改进研究从未停止。鉴于可获得数据基础和大数据方法的改变，交通规划模型的工作基础发生了巨大变化，本研究将结合新数据基础探索交通模型的实践应用和优化提升。

1 交通规划模型演进及改善机遇

1.1 交通规划模型研究进展

60多年来，国内外学者结合外部技术进展不断尝试完善交通规划模型理论、技术和方法。在四阶段模型方面，Fosgerau等[4]利用半参数估计技术来优化方式划分模型。Florian等[5]使用出行分布、方式划分和交通分配联合模型来解决各阶段一致性的问题。Boyce等[6- 7]开展了利用反馈技术弥补各阶段不一致的问题，并通过对模型反馈结构及迭代过程中成本函数计算方法优化来提升交通模型效率。Kumar等[8]提出了通过反馈来实现四步骤需求建模的后处理技术。屈云超等[9]对反馈模型的权重系数进行了研究。对活动模型的理论探索始于20世纪70年代至80年代。Hägerstrand[10]的工作首次探讨了出行活动和时空概念之间的关系。Jones[11]很好地总结了这项工作，并提出了满足出行者的角色、需求、时空联系及人际关系多重约束条件的家庭出行模式识别理论。McFadden[12]提出的随机效用最大化(RUM)理论为经验ABM奠定了基础。活动模型在21世纪初逐渐得到推广和应用，目前美国约有30多个城市[13]开始使用基于活动理论的交通规划模型，模型理论也正逐步从最佳理论走向最佳实践，开发和使用也日趋成熟。Adler 等[14]首先将单维度模型扩展到多维活动-出行模式，包括出行链、出行特征、出行模式、目的地选择等。Bowman等[15]首次提出的“个人日常活动模式”模型遵循了总体日常活动出行模式的概念。之后Bowman等[16]将这种方法概括为白天活动计划模型，它的应用包括波特兰地铁模型[16]和萨格拉门托基于活动的模拟模型(SACSIM)[17]等。纽约最佳实践模型(NYBPM)[18]采用了日常活动模式协调模型，通过协调家庭成员出行活动计划及出行模式之间的相互关系，增强了个人日常活动模式模型，是一个以家庭为研究对象的分析模型。分析既有的ABM模型结构不难发现有两个核心的内容：人口合成模型[19]和活动仿真模型[20]。通过人口合成模型来模拟家庭的人口信息、工作地、学校位置等基本位置信息，再结合活动仿真模型来模拟出行活动，产生的问题是人口合成模型所得到的职住对应关系等是模拟的结果且是变化的，而事实上对常住人口而言家庭住址、成员的工作和学校基本固定。人口合成模型所带来的误差也必将导致后续的活动仿真的可靠性也无法保证。

总体来说，虽然经过60多年的发展，交通模型技术取得了长足的进步，理论体系日趋完善，为城市交通规划决策和运行管理做出了重要贡献。但受制于基础数据，无论是集计模型还是非集计模型均在应用方面存在一定的局限性。基于城市居民出行的一般规律性和近年来手机信令数据的广泛应用，本研究提出了基于出行者稳定性的交通规划模型结构，通过移动位置数据建立人口的职住对应关系，结合驻点分类技术明确人口生活出行分布，以此分析通勤交通和生活出行这两类城市居民基本稳定的出行活动(活动起终点和活动时间均相对稳定)。这类相对稳定的出行活动约占城市出行总量的60%以上，其中早高峰时段占比达83%。因为稳态出行在城市活动中的大份额占比，通过对城市稳态出行的准确分析显然有助于提升模型的精度。最后，以广州市花都区为例，对比分析了基于传统四步骤模型的出行分布预测结果与基于出行者活动稳定性模型的差异，验证了新方法计算结果的可靠性。

1.2 四步骤交通模型的局限性

四步骤交通模型理论对出行的表达基于单次出行，这也带来了对交通模型解释上的一些问题。例如，四步骤交通模型是基于Trip的模型，忽略了相邻两次出行之间的关联性；四步骤模型是集计模型，个体行为因素考虑不足，同时不能反映家庭成员之间的联系；因为四步骤模型的交通分配为最后一个步骤，这也使得出行分布和方式划分的出行成本处于非平衡条件；由于使用人口就业作为输入条件，这使得土地利用独立于交通需求预测模型，难以响应交通与土地利用的互动关系。四步骤模型将出行解释为去做什么(出行目的)、去哪里(出行分布)、怎么去(方式划分)、走那条路(交通分配)，再加上什么时候去，对单次出行的表达式非常完整，既有问题并不能否定四步骤模型对单次出行活动根本特征的表达是充分有效的。然而事实上，四步骤模型在运用过程中容易产生偏差，特别是基于重力模型计算所得的出行目的地选择，完全忽略了出行者的社会属性，包括出行者的家庭住址和工作岗位相对稳定要素的影响。此外，四步骤模型建立之初，数据采集手段无法支持全样本的职住关系等，利用数学规划方法来求解出行空间分布，变成退而求次的方法。

1.3 基于活动模型的局限性

活动模型(ABM)在一定程度上可以理解为四步骤模型的加强版，虽然解决了四步骤模型的部分问题，如通过人口合成模型[17]解决了交通和土地利用互动问题，对个体出行行为考虑也比较充分，但产生的问题是所需输入数据要求更加严格，且产生了运行耗时超产的巨大缺陷。例如2012年Hadi等[21]完成的Jacksonville的ABM模型，人口规模大约120万，根据设置条件的不同，单方案的运行时间至少为2.5天，最多高达31天。即便是人口不足20万的小城Shasta的ABM模型单方案运行时间也需要5.5～8.0 h[22]。显然，较长的运行耗时难以满足快速响应的需要。此外，人口合成模型并没有从根本上解决模型中出行者的社会属性问题，其职住对应关系仍然是通过各类选择模型模拟计算得到，与实际必然存在偏差。假定可以获得真实的职住对应关系，这将带来巨大的隐私风险和隐患，所以直接获得真实的个体职住地数据不可行。此外，活动模型的优势仍然在于对常住人口的稳态出行的解析，包括通勤、通学和生活购物等，而对于偶然出行的解释依据不足。同样，活动模型对流动人口出行活动解释能力有限。

1.4 移动位置数据应用于交通建模带来的机遇与挑战

随着科技发展，越来越多的大数据资源被应用到出行行为研究中，特别是以手机信令数据为代表的各类移动通信位置数据和互联网位置数据被逐渐应用到出行行为分析[23- 25]中，这一方面使得对人的行为与活动追踪成为可能，另一方面也为交通模型众多不确定的输入提供了进一步界定可能。第一，人口母体更加明确。以往人口数据更多的只能依赖统计局、公安局和民政局等政府部门提供的统计数据，但出于种种原因各部门的数据往往差异较大，给使用带来较大的困扰。第二，就业岗位分布更加准确。经济普查所得的就业岗位数为机构注册地，注册地和实际工作地分离严重。移动通信和互联网位置数据等大数据资源分析所得的岗位数据更加准确。第三，职住之间的对应关系得以建立。传统统计数据人口和岗位之间是互相独立的，通过长周期的移动通信和互联网位置数据分析，可以建立人口和岗位之间的对应关系，为交通需求分析打下更坚实的基础。第四，移动通信和互联网位置数据可以用于人的活动的识别，包括基于移动位置数据可以增加对城市稳态出行(包括通勤和生活出行)解析的精度；可以大规模揭示流动人口出行特征和活动规律；可以弥补传统问卷调查受访对象存在可能涉及隐私出行瞒报和遗忘出行漏报[26]的情形，挖掘沉默需求。当然，移动位置数据资源本身也存在一定的问题，比如数据获取困难、模糊地址、缺少分类信息、一人多号、位置漂移等，这也需要在数据挖掘过程中和其他传统数据进行关联性分析和校验。

通过以上分析可知：既有交通模型结构的缺陷主要来自于城市稳态出行要素的不确定性；移动位置数据通过建立职住对应关系、辨识生活出行驻点，能够弥补既有交通模型结构中稳态出行要素可靠性问题，同时利用交通分区作为数据采集单元，可以避免数据精度过高带来的隐私泄露矛盾。此外，移动通信数据能够提升对流动人口出行活动分析的精度。总体来说，移动位置数据有助于弥补既有交通模型的不足，促进交通模型精度的提升。

2 基于出行者稳定性的四步骤模型结构设计

2.1 出行者稳定性定义与出行目的设定

出行者稳定性是指城市人口具有相对稳定的活动特征，包括居住地和工作地的相对固定，学生上学的学校是固定的，日常活动的场所(如买菜、购物、健身等)也相对固定且在一定区域内呈现一致性，日常活动组织结构见图1。因为出行者在一定时期内具备稳定性的特征，城市稳态出行是基于此特征要素的出行活动，主要包括通勤、通学和生活服务等出行起终点固定且活动时间和活动周期等均相对固定的出行活动。城市稳态出行在城市出行总量中占比较高，第五次北京城市综合交通调查报告[27]显示六环内上下班、上下学和生活类出行占比为98.6%，上海第五次综合交通调查报告显示上下班、上下学和日常生活出行占比为73.6%[28]。由此可以看出，城市稳态出行在出行总量中占主体，准确分析其活动特征有助于提高模型精度。根据出行活动频次和规律的不同，将城市出行活动划分为稳态出行和偶然出行，具体如图2所示。

传统四步骤模型中出行目的主要分为基家出行和非基家出行两大类，具体可以细化为基家工作、基家上学、基家生活和基家其他、非基家工作与非基家其他等6类，或者其他类似划分方式，强调的是出行目的和出行一端性质的稳定性，而另一端则依赖满足条件的最优化选择求解，相当于每进行一次求解进行了一次洗牌，无法体现出行者的稳定性属性。新的出行目的划分更强调对出行者社会属性稳定性的利用，包括住所、工作场所、学校及日常生活驻点的稳定性，充分响应了出行者自身的客观可能活动范围，而不是传统的最优化求解方法，更加能够符合城市实际。

图1 基于空间联系的出行者活动分类

图2 基于稳态出行和偶然出行的出行目的分类

2.2 四步骤模型组合与改进设计

关于四步骤模型结构实现和变化源自Williams[29]对交通方式划分模型次序的探讨，提出了4种可行的四步骤模型实施结构，分别为：①交通方式划分与交通生成模型同步实现(回归类模型)；②交通方式划分位于交通生成模型和交通分布模型之间(转移曲线类模型)；③交通方式划分与交通分布模型同步实现(重力模型类模型)；④交通方式划分位于出行分布和交通分配之间(方式竞争类模型)，各类模型结构见图3。

20世纪90年代Boyce等[30]在四步骤模型结构中引入了迭代和反馈以减少模型理论各阶段不一致的影响，最终形成了通用的标准四步骤模型结构。各种形式的四步骤模型结构中，出行分布有两种形式，独立运行或者与方式划分模型同步实现。标准四步骤模型结构中引入反馈之后，出行分布是随着出行成本(或者广义费用)变化的，这与实际城市与交通系统中出行者大部分活动的分布稳定性相矛盾。为此，本研究提出基于出行者活动稳定性的改进四步骤模型结构，对于城市稳态出行采用出行生成和出行分布同步实现的建模方法，对于偶然出行/弹性出行采用标准四步骤模型结构，符合出行成本约束下出行目的地可选择的基本规则。具体见图4。新的模型结构中对于稳态出行分布，充分考虑了出行者的个人属性(居住地、工作地)和区域差别化(社区生活圈的稳定性)，计算结果更能符合城市交通活动的实际状况。

图3 四步骤模型组合结构

图4 改进的四步骤模型结构设计

3 案例应用与效果比较

3.1 案例概况

广州市花都区面积970平方公里，2018年末常住人口109万，管理人口155万，从业人口70万(其中区内就业人口63.6万)，就业岗位约79.6万，道路网络长度约2 397公里。结合行政边界、水系、交通网络和土地利用等条件，共划分交通小区304个，交通大区12个(见图5)，用于交通方案分析和测试。利用移动通信位置数据分析的职住联系矩阵作为基准情形和输入条件，假定其为已知正确出行OD矩阵，利用其特征，对传统出行分布模型进行标定和校验，以验证传统模型对出行者活动稳定性解释的不足。

图5 花都区交通模型交通分区

3.2 分析方法

传统出行分布模型[2]主要包括重力模型、最大熵模型、介入机会模型及增长率模型(Fratar、Furness)等方法，其中对于增长变化较快的城市应用最为广泛的模型为重力模型，其表达式为

Tij=αOiDjf(cij)

(1)

式中:Tij为交通小区i和j之间的出行量；Oi为交通小区的发生量；Dj为交通小区的吸引量；cij为交通小区i和j之间的出行成本；f(cij)为广义出行成本函数，常用的形式有：

f(cij)=exp(-βcij)

(2)

(3)

(4)

其中α、δ和β为模型参数。

应用过程中为增加模型对城市实际的适应性，使用带K系数重力模型[31]或者三维约束重力模型[32- 33]等控制区域之间的出行联系，以提升交通模型预测的可靠性。基于交通小区的K系数矩阵标定难度非常大，所以通常用交通大区来表示，其定义为反映交通分区之间社会经济联系的系数。现状K系数可以理解为交通大区之间的实际出行交通量和标准重力模型计算结果的比值。传统方法中结合城市交通运行调查数据，有可能推算出基于交通大区之类的区域间出行联系，作为区域出行联系的控制值。带有K系数矩阵的重力模型表达式为

(5)

式中,Pi为交通小区的出行产生量,Aj为交通小区j的出行吸引量,civ为交通小区i和v之间的出行成本,f(civ)为交通小区i和v之间的出行阻抗函数,Kij、Kiv分别为交通小区i和j之间及交通小区i和v之间的出行分布修正系数,n为网络中的交通小区数量。

改进四步骤模型结构与传统模型的主要差别在于对现状的解析。通过大数据手段识别固定OD点对、固定出行目的、高频发生的城市稳态出行，可以理解为用现实的出行分布来代替传统模型结构中运用重力模型、熵模型等方式进行最优化求解模拟得到的现状稳态出行分布。为此，本研究假定职住联系OD矩阵为目标基家工作出行(HBW)出行OD矩阵，并以此矩阵计算各交通小区的出行发生量P和出行吸引量A，同时利用路网模型计算交通小区之间的特征指标矩阵并统计目标出行矩阵的出行距离分布(TLD),对模型进行标定计算，阻抗函数参数(复合函数),α、δ和β取值分别为0.526 593 67、-0.381 936 37和-0.421 382 24。区域联系K系数矩阵见表1。

3.3 模型结果的比较分析

以重力模型阻抗函数标定结果和K系数矩阵作为参数，结合PA矩阵和出行阻抗矩阵作为输入条件，对模型进行计算，通过基准情形、标准重力模型和带K系数矩阵重力模型3种方法计算得到相应的行分布矩阵。以下分别从出行距离分布、大区空间联系和小区预测结果3个方面进行比较。

从图6出行距离分布曲线来看，带有系数矩阵约束条件的重力模型计算结果较标准重力模型能够更好地与基准情形相匹配，出行距离分布拟合程度更高。从平均出行距离分布来看，基准情形为4.17 km，而标准重力模型为3.75 km，K系数重力模型为3.81 km。平均出行距离计算结果也表明K系数重力模型的计算结果更接近实际。总体来说，K系数矩阵对区域之间的社会经济联系有较好的解释作用，同时也说明了标准重力模型对出行空间分布解释的局限性。但从具体曲线形态来看，无论是标准重力模型还是K系数重力模型与目标值均存在明显差异，标准重力模型短距离出行(0～3 km)明显低于目标值，而4～13 km的出行量明显大于目标值，K系数重力模型虽然有一定修正，但仍存在一定差异。此外，目标值的多峰特征(1-2、12-13和20-25共3个点)未能得到反映。

表1 交通大区K系数矩阵

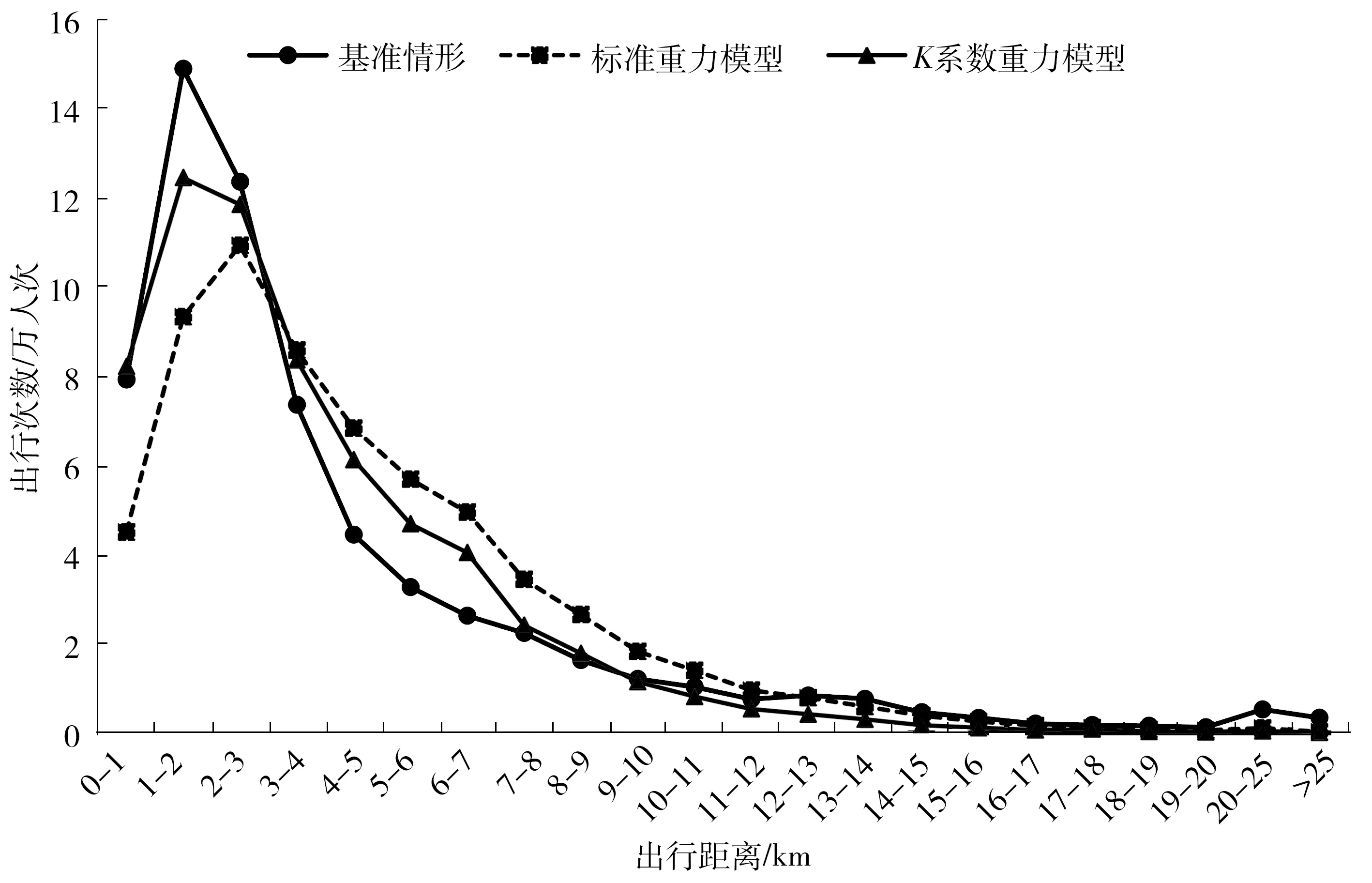
图6 基准情形出行距离分布曲线与重力模型模拟值比较

以基准情形为参照，对应全部12个交通大区144个OD点对的计算结果，标准重力模型和K系数重力模型的模拟结果在交通大区层面均能较好地拟合，拟合优度r2达到0.99以上(见图7)。

从出行距离分布和交通大区出行联系来看，建立和标定的模型已经具有非常高的精度，能够比较准确地反映城市的出行特征。但从交通小区层面来看，标准重力模型和K系数重力模型计算结果和基准情形的拟合优度r2均不到0.65(见图8)，甚至存在OD点对之间实际出行需求为0、但有较大预测值的情形。这也说明了传统基于数学规划的出行分布预测方法能够在一定程度上实现预测的要求，但在小颗粒度分析上容易存在偏差，而且这是在具有比较高精度的出行距离分布和大区出行联系的基础上完成的。

以上分析表明，在较为准确的整体数据支持下，通过数学优化求解的方法实现较高精度的区域层级的出行预测是一种行之有效的方法。更精细颗粒度和更高准确性的出行活动分析结果，表明传统数学优化方法计算所得的交通小区层次的联系仍可能存在较大偏差和缺陷。此外，K系数矩阵的获取依赖较为准确的区域联系交通出行指标，这对基础数据可靠性也提出了更高的要求。所以，有必要也有条件引入更加准确的输入数据，以提升交通模型精度。

图7 交通大区之间出行量的重力模型预测值与基准情形的比较

图8 交通小区之间出行量的重力模型预测值与基准情形的比较

4 结语

本研究提出了利用出行者活动稳定性特征改进出行分布模型的技术方法，并利用实际数据对方法进行了验证。计算结果表明，基于传统最优化模型结合高精度的区域交通出行需求约束条件、可以较好地完成交通大区级别的出行需求预测，但该方法难以满足交通小区层级更精细的交通分析需求。大数据技术发展至今，已经有条件实现更加准确的出行活动研究，特别是工作、就学和生活等稳态出行，在减少交通模型计算量的同时，可以更加准确地解析城市实际交通状况。基于出行者活动稳定性特征的需求分析模型的特点，也决定了它能够很好适应城市现状和近期交通预测模型的需要。考虑交通模型中长期预测的功能，需要开展基于既有现实条件的城市未来推演模型研究，在尊重城市现状的前提下，充分考虑出行者的稳定性特征，开展既有人口迁徙，包括居住地、工作地变迁，并利用既有人口的职住关系等特征推算迁入人口和自然增长人口的职住选择，进而形成和发展对未来的预测能力。这要求交通规划模型的开发建设是一个渐进的过程，在适应新的数据要求的同时进一步完善应用框架和理论方法。此外，出行者活动稳定性的特性具有进一步延伸的可能，包括出行者交通方式的稳定性、路径的稳定性等，可以结合数据基础的变化在未来开展进一步研究。