工程机械柱塞泵变载荷工况故障诊断方法
唐宏宾 傅政 邓习树 黄毅
(1.长沙理工大学 汽车与机械工程学院,湖南 长沙 410114;2.三一汽车制造有限公司,湖南 长沙 410100)
柱塞泵是工程机械液压传动系统的动力源和核心元件[1- 2],其运行状态与服役性能直接影响着工程机械的施工质量和运营安全[3- 4]。针对柱塞泵的健康监测及故障诊断,国内外学者开展了广泛的研究,目前主要采用的是数据驱动方法。该方法首先测量柱塞泵不同健康状态的动态信号,然后利用信号处理技术提取故障特征,再将故障特征输入到分类器中进行故障模式识别。由于柱塞泵本身固有的机械振动、流体的压缩性及流-固耦合作用,使得现场采集的信号往往会被各种干扰影响,导致信噪比低,故障特征微弱,传统的信号处理方法难以有效提取性能状态信息。因此,小波(小波包)分析[5]、经验模式分解[6]、局部特征尺度分解[7- 8]、增强聚类分割[9]等方法在柱塞泵故障特征提取中得到了广泛应用。传统的模式识别方法,如神经网络[10- 11]、支持向量机[12- 13]等虽然能对柱塞泵的健康状态进行有效检测,但检测准确率很大程度上取决于提取的故障特征。近年来兴起的深度学习方法可以直接从原始信号中提取敏感特征,在柱塞泵的状态故障诊断中也得到了应用[14- 16],取得了较好的效果。
数据驱动方法有效促进了柱塞泵状态监测及故障诊断技术的进步,但在实际应用中还受到一些限制:一是工程机械实际运行中的负载是不断变化的,因此现场采集的动态信号受柱塞泵健康状态和负载波动的耦合作用,这增加了数据驱动方法检测故障的难度;二是数据驱动方法的可靠性和准确性在很大程度上取决于样本数量,而柱塞泵实际运行中不同健康状况、不同负载下的大量数据通常难以获取;三是数据驱动方法对柱塞泵的动力学特性,尤其是故障状态的动力学特性缺乏深入分析,难以准确描述故障机理。
基于模型的诊断方法可以克服上述问题,这为柱塞泵的故障诊断提供了一种新的思路[17]。然而,由于柱塞泵结构的复杂性和机构与流体之间的液-固耦合效应,使得直接利用解析方法建立柱塞泵的数学模型困难重重,而虚拟样机技术的发展和进步为建立柱塞泵准确的动力学分析模型提供了可能。虚拟样机技术在柱塞泵的结构设计及优化[18]、减振降噪[19]、性能分析[20]等方面已经得到了一定的应用。
基于此,本研究提出了一种基于虚拟样机的工程机械柱塞泵变载荷工况故障诊断方法。首先构建了柱塞泵的虚拟样机模型并进行了验证,然后在模型中模拟了柱塞泵的滑靴松动故障,对柱塞泵不同健康状态、不同负载下的动力学行为进行了分析,并基于分析结果提出了一种柱塞泵变载荷工况的诊断方法,最后通过试验验证了该方法的有效性。
1 建模基础
柱塞泵中单个柱塞的运动示意如图1所示,原点“O”位于柱塞运动轨迹的上止点与下止点的中点位置,x轴为轴向,y轴、z轴均为径向。

1—柱塞;2—滑靴;3—斜盘;4—柱塞腔
将A点(上止点)作为柱塞球头的初始位置,设缸体旋转速度为ω,当柱塞随缸体旋转角度φ时,则球头的位置坐标为:

(1)
式中,γ为斜盘倾角,R为柱塞孔分度圆半径。则第i个柱塞直线往复运动的速度和加速度分别为:
vi=ωRtanγsinφ
(2)
ai=ω2Rtanγcosφ
(3)
则单个柱塞孔的瞬时流量为
(4)
式中,d为柱塞孔直径。
由于柱塞泵共有n个柱塞沿缸体一周均匀分布,相位角为
(5)
柱塞泵出口的瞬时流量为排油区内单个柱塞的瞬时流量相加的和,即
(6)
显然,柱塞泵的流量脉动频率为
(7)
2 虚拟样机构建
2.1 多体动力学模型
首先利用三维建模软件SOLIDWORKS建立了图2所示的国产SCY系列的柱塞泵(包含7个柱塞)三维实体模型,再将三维模型导入到多体动力学仿真软件ADAMS中,根据图1所示柱塞泵各部件的运动学和动力学关系,对各部件添加表1所示的约束副,然后添加载荷、驱动等,即得到了图3所示的柱塞泵多刚体动力学模型。
为了获取柱塞泵的动态响应,对泵壳和端盖进行了柔性化处理,如图4所示。首先将SOLIDWORKS中泵壳和端盖的三维实体模型保存为Parasolid格式并导入到有限元分析软件ANSYS中,然后在ANSYS中选择单元类型为SOLID186实体单元并定义材料参数,选用智能划分网格方式进行网格划分,在柔性化的零部件与外部零件接触面的几何中心位置创建外部节点,在创建完成柔性体的外部节点和定义刚性区后,通过Export to ADAMS设置零部件模态分析的模态阶数,输出MNF中性文件,再在ADAMS中读入此文件替换原有的刚体模型,即可得到柱塞泵的刚-柔耦合模型。
2.2 液压模型

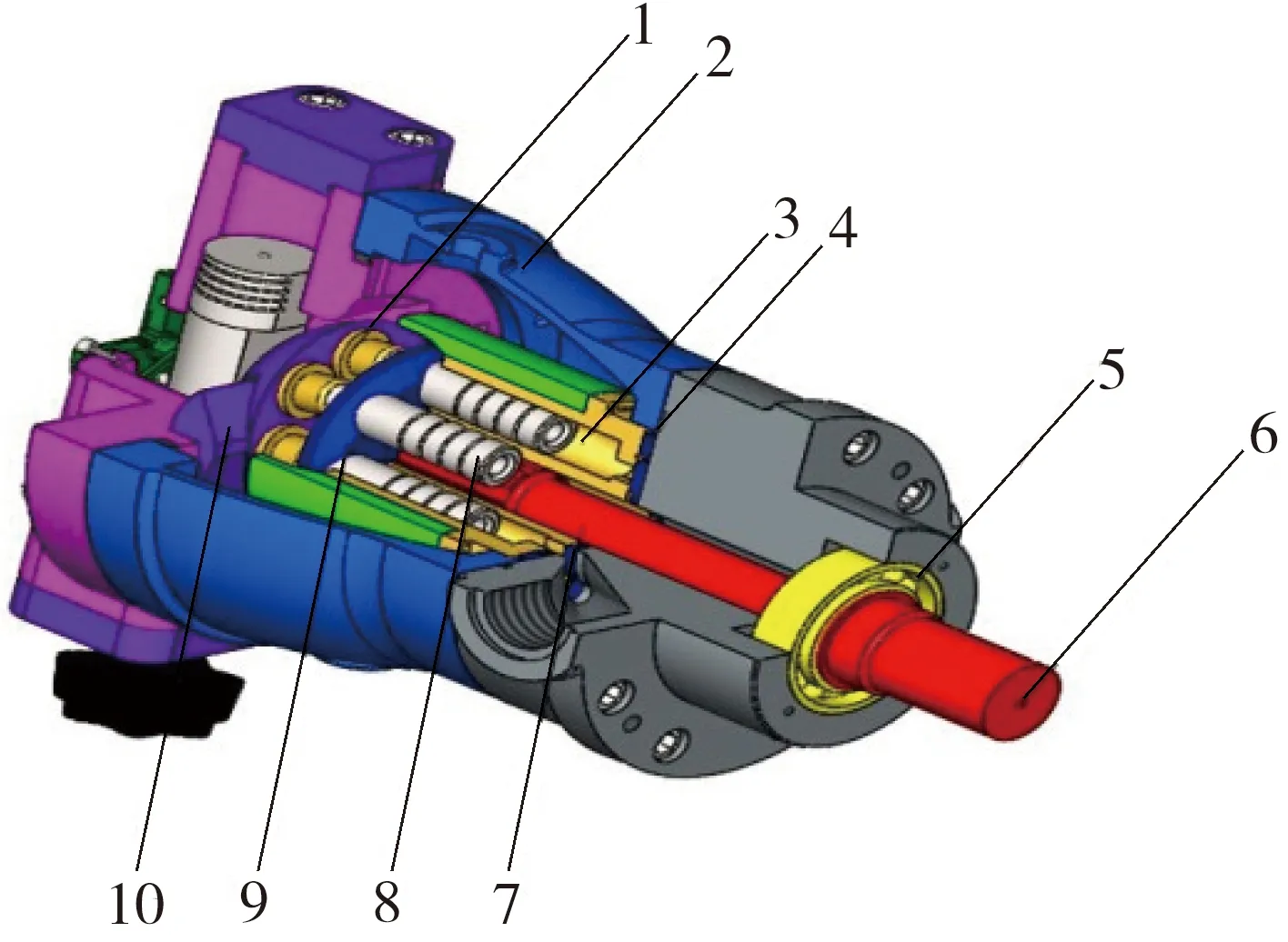
1—滑靴;2—泵壳;3—柱塞腔;4—配流盘;5—轴承;6—驱动轴;7—缸体;8—柱塞;9—回程盘;10—斜盘

表1 柱塞泵约束副
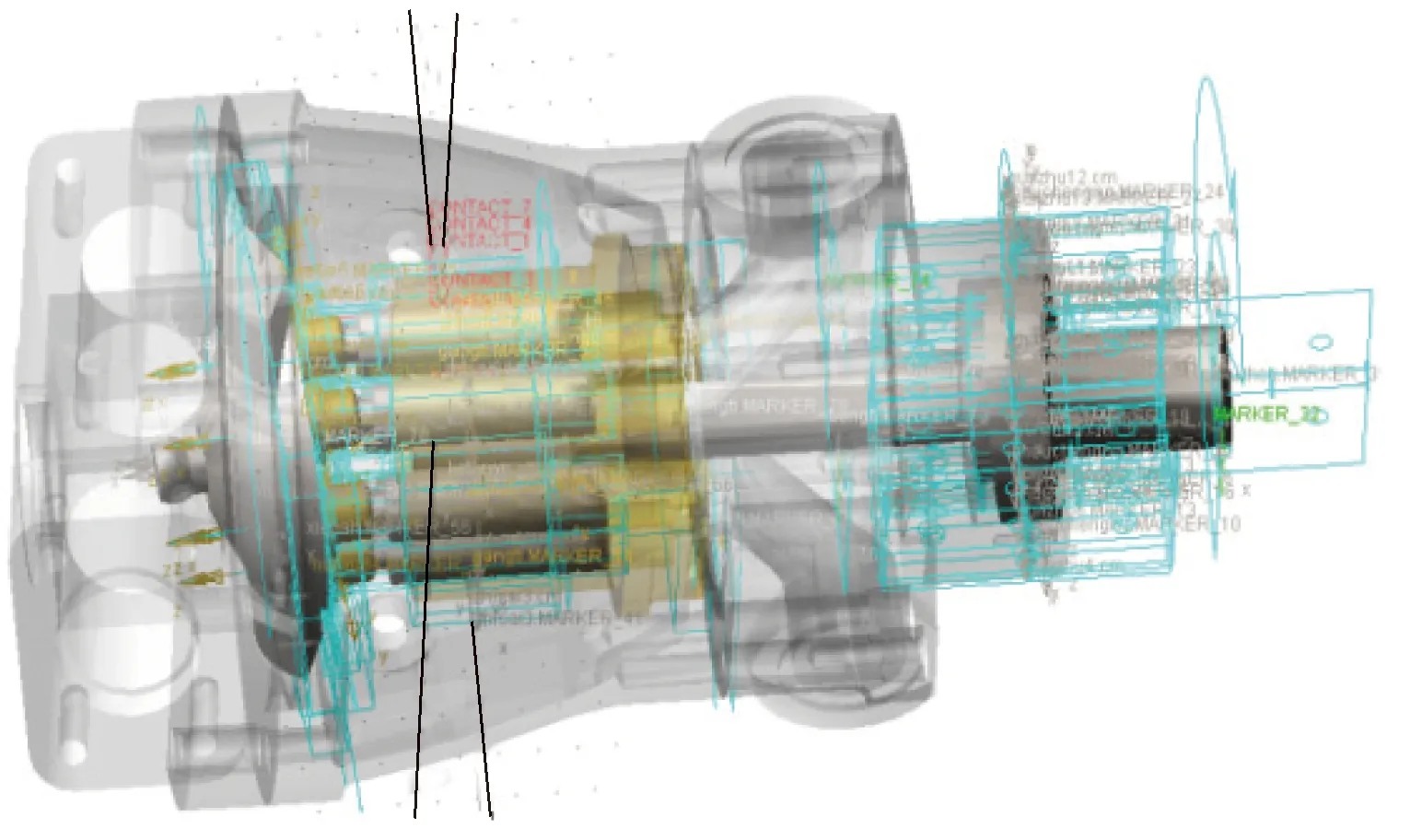
图3 多刚体动力学模型

图4 柔性体模型

1—配流盘模型;2—柱塞位移模型;3—流量模型;4—qv1;5—qv2;6—qv3
图6 柱塞泵液压模型

表2 液压模型参数
2.3 联合仿真分析
进行多体动力学模型和液压模型的联合仿真,需要对两个模型之间的交换变量进行设置,如图7所示。

图7 变量交换示意图
联合仿真分析时,首先在ADMAS中进行多体动力学仿真,给定柱塞泵的驱动轴一个转速后,可以得到7个柱塞的运动学参数(位移、速度和加速度等),然后通过ADAMS/Controls模块导入AMSIM,通过液压系统仿真可以得到7个柱塞孔中的液压力,再将该液压力载入ADAMS,即可实现多体动力学模型和液压模型的联合仿真。仿真设置的主要参数如下:驱动轴转速为1 500 r/min,转速从0到稳定转速的时长为0.2 s,负载压力为23.5 MPa,仿真总时长为1 s,仿真步长为0.000 2 s,模型的分析类型设为Dynamics。
仿真分析结果与理论计算结果进行了对比分析,结果如图8和表3所示。其中,“理论计算”是从式(1)-(7)获得的计算结果,“仿真分析”是通过虚拟样机联合仿真得到的分析结果。
从图8中可知:由于仿真分析中,驱动轴转速设置为在0.2 s之内从0增加到1 500 r/min,因此柱塞速度、加速度及柱塞泵流量等参数0.2 s后与理论计算得到的参数基本吻合。从表3可以看出:仿真分析和理论计算得到的柱塞运行的最大速度、最大加速度的相对误差分别为0.05%、0.07%,均可以忽略不计;而仿真分析得到的柱塞泵出口流量小于理论计算结果,两者的误差达到了5.18%,这是由于建立的虚拟样机模型包含了泄漏模块(见图4),考虑了柱塞泵实际运行中3个位置的泄漏,而理论计算公式中并未考虑泄漏。因此,本研究建立的虚拟样机能够更好地描述柱塞泵的运行状况。
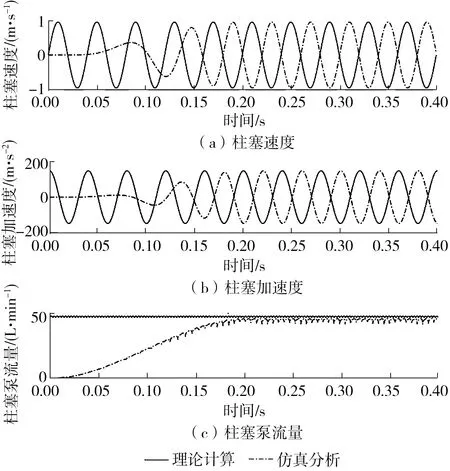
图8 理论计算与仿真分析对比图

表3 理论计算与仿真分析对比

仿真分析得到的柱塞泵出口的压力及其频谱如图10所示。由图10(a)可知,由于柱塞泵工作过程中7个柱塞腔依次与出油口相连,因此出口压力始终处于高压区,压力值即为设定的负载压力23.5 MPa,且有一定的压力脉动。由图10(b)可知,在式(7)计算得到的柱塞泵的流量脉动频率175 Hz及其倍频处有明显的峰值。

图9 单个柱塞腔压力

图10 柱塞泵出口压力及频谱
以上结果表明:利用柱塞泵的虚拟样机得到的仿真分析结果均与柱塞泵的实际工作状态和流体特性相吻合,因此本研究建立的虚拟样机模型能够准确地模拟柱塞泵的运行状态。
3 松靴故障模拟及动力学响应分析
3.1 故障模拟
滑靴松动是柱塞泵的一种常见故障。正常状态下,柱塞球头与滑靴之间应保持合理的间隙。但由于制造和装配误差,以及柱塞直线往复运动时受到的作用力,会使柱塞球头与滑靴接触面之间的磨损加剧,从而使间隙不断增大,导致柱塞泵的异常振动,甚至会使柱塞球头脱离滑靴,产生严重后果。
在上节构建的柱塞泵正常状态的虚拟样机模型中,7个柱塞球头与滑靴的约束方式均设置为球铰副。为了模拟松靴故障,将柱塞球头与滑靴的约束改为了间隙副,并且对柱塞球头的几何尺寸进行了修改,其直径与正常状态相比分别减小0.05 mm和0.10 mm,代表松靴故障的严重程度。因此,本研究共构建了柱塞泵3种状态的虚拟样机。
3.2 动力学响应分析
通过对柱塞泵在3种不同健康状态下的动态响应仿真分析发现:压力信号没有明显变化,即压力信号对松靴故障不敏感;而泵壳上的振动信号的变化较为敏感。柱塞泵3种状态下的振动信号及其频谱如图11、图12所示。其中,x轴(轴向)、y轴(径向)、z轴(径向)的方向和图1所示相同。

图11 柱塞泵3个方向的振动信号

图12 柱塞泵3个方向振动信号频谱
从图11可以看出:滑靴松动将导致3个方向的振动增加;松靴故障越严重,振动信号增加得越显著;轴向振动(x轴)的增加比径向振动(y轴、z轴)的增加更为明显。从图12可以看出:在柱塞泵的供油脉冲频率(175 Hz)及其倍频处有明显的峰值;滑靴松动故障时,振动信号在频域的能量也会增加;松靴越严重,振动信号能量增加得越显著;轴向振动信号能量增强得更为明显。
通过以上分析,笔者选取了轴向振动信号作为柱塞泵松靴故障的敏感信号,并提取了反映其能量变化的参数——均方根值(RMS)作为滑靴松动的故障特征,其定义为
(8)
4 变载荷工况松靴故障诊断
4.1 变载荷工况动力学响应分析
上节中的结论为柱塞泵的故障诊断提供了解决思路,但其动态响应都是在恒定负载下得到的。然而,柱塞泵实际工作过程中,其负载是连续变化的,其动态响应不仅受健康状态影响,还受外界负载的影响,这增加了故障诊断的难度。由于连续变化负载的模拟较为困难,本研究选用了4种离散的恒定荷载(5.0、10.0、15.0和23.5 MPa)来分析载荷变化对柱塞泵动态响应的影响。在工程实际中,当用较高的采样频率采集其动态信号时,可以近似认为在短时间采样过程中的负载是恒定不变的。
通过联合仿真得到的柱塞泵在不同负载条件、不同健康状态下轴向振动信号如图13所示,从中可以看出:柱塞泵在正常状态下,其轴向振动会随着负载的增加而增加,而松靴故障的发生也会导致轴向振动的增加,故障越严重,振动增加的越显著。
为了更好地分析负载和松靴故障对轴向振动信号产生的耦合影响,将由式(8)计算的故障特征绘制成图14以便观察。从图14中可以清楚地看到:RMS虽然确实随着负载的增加而增加,但当柱塞泵处于不同的健康状态时,负载增加引起RMS增加的趋势是不一样的,松靴故障越严重,均方根值随着负载的增加而增大得越快,即梯度越大。通过回归分析,得到了柱塞泵3种不同健康状态随负载变化的趋势线,如式(9)所示:

(9)

图13 不同负载条件、不同健康状态下的振动信号
由式(9)可知,柱塞泵正常状态下,趋势线的梯度为0.040 8,轻微故障情况下的梯度为0.072 4,严重故障的情况下的梯度为0.156 0。显然,松靴故障越严重,趋势线的梯度越大。因此,可以通过观察轴向振动信号RMS增长的趋势(即梯度)来检测松靴故障。

图14 轴向振动信号的RMS
4.2 诊断流程
通过以上分析,本研究提出了一种在变载荷工况下对柱塞泵松靴故障进行诊断的方法,其步骤为:①在短时间内(例如1 s)采集轴向振动信号;②将收集的振动信号划分成相等的部分(例如,4个部分);③计算每个分段信号的均方根值;④计算均方根趋势线的梯度;⑤基于均方根趋势线梯度检测松靴故障。
5 试验研究
5.1 试验平台
为了验证上节提出的故障诊断方法的有效性,在图15所示的试验台上开展了试验研究,试验台工作原理如图16所示。该试验台主要由动力源、液压控制系统、信号采集系统、载荷模拟装置等4部分组成,电动机带动柱塞泵旋转,再由柱塞泵通过液压控制阀驱动液压马达,液压马达的输出轴与测功机相连,通过测功机的控制器可以改变液压马达的负载。信号采集系统用于采集柱塞泵运行中的压力、振动等信号,并将信号传至计算机进行分析和存储。
本实验中选用的柱塞泵为力士乐A11VLO190,其有9个柱塞,额定压力为35 MPa,最大排量为190 mL/r。加速度传感器安装在泵壳上,用于采集轴向振动信号,压力传感器安装在柱塞泵出口位置。数据采集系统选用的是DEWE- 2521数据采集仪。在试验中,分别对正常工作和滑靴松动故障下的柱塞泵进行交替测试,转速均设定为1 600 r/min,采样频率为10 kHz,负载分别为5、10、15、20 MPa。

图15 试验平台

图16 试验台工作原理图
5.2 故障诊断
当负载压力设置为10 MPa时,试验中采集的正常泵和松靴故障泵的振动信号及其频谱如图17所示。从图17(a)和17(b)的时域波形看,发生滑靴松动后振动幅值有所增加。从17(c)和17(d)的频谱中可以清楚地观察到,在柱塞泵的脉动频率(240 Hz)及其倍频处均有明显的峰值,并且松靴故障的发生也使得频域的能量整体增强。上述现象均与上节中仿真分析的结论是一致的。
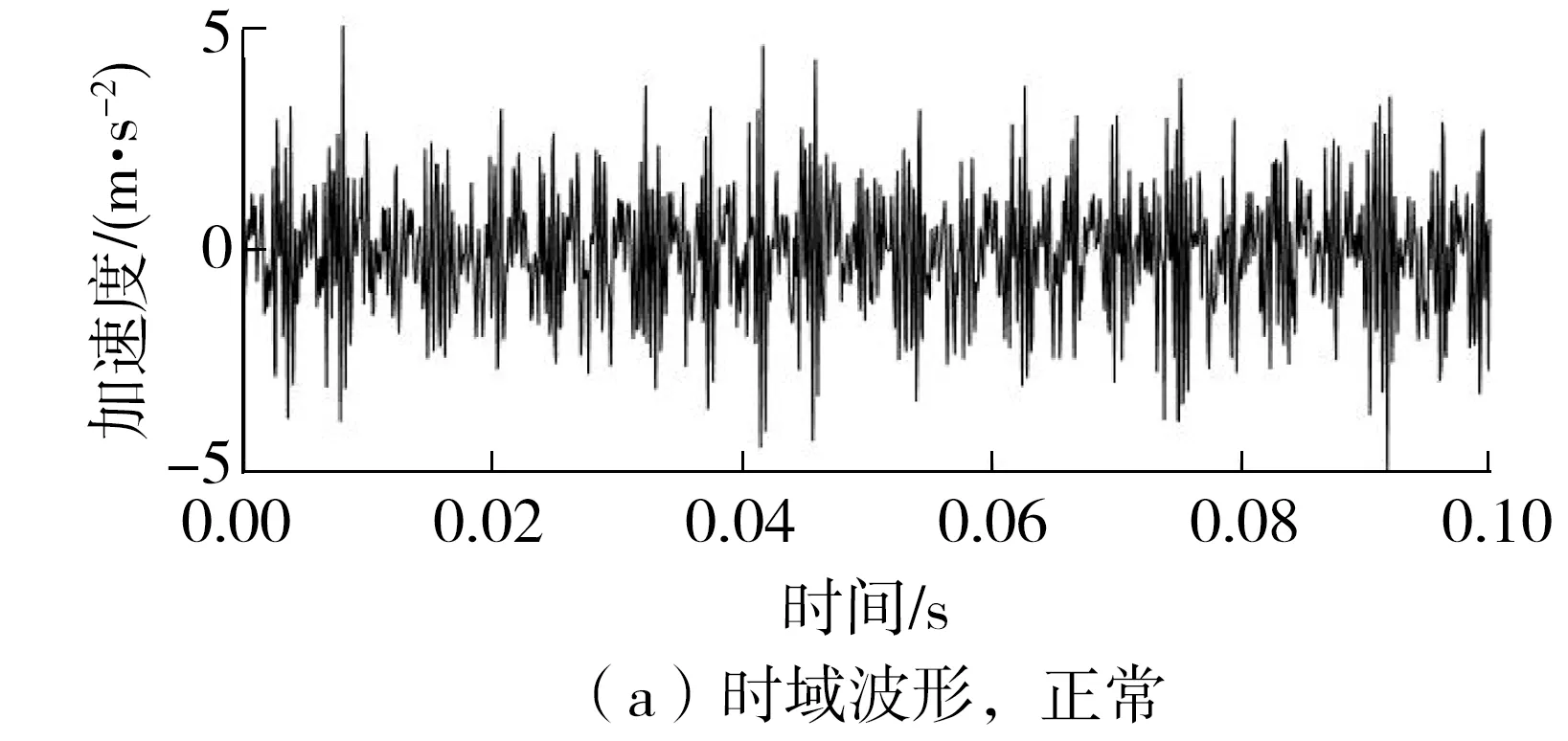
图17 正常泵和故障泵的轴向振动信号
试验得到的柱塞泵在不同负载条件、不同健康状态下轴向振动信号的时间波形如图18所示,由式(8)计算的故障特征如表4所示。从图、表中可以看出:不管柱塞泵处于正常状态还是故障状态,轴向振动的RMS均会随着负载的增加而增加,并且松靴故障的发生也会导致RMS的增大。这与仿真分析中得到的结论也是一致的。
根据图15中的故障诊断流程,将表4中的所有RMS值数据绘制成曲线,如图19所示。不同负载下的RMS趋势线方程分别为:

(10)

图18 实测不同负载条件、不同健康状态下的振动信号

表4 柱塞泵不同工况下的轴向振动的RMS值
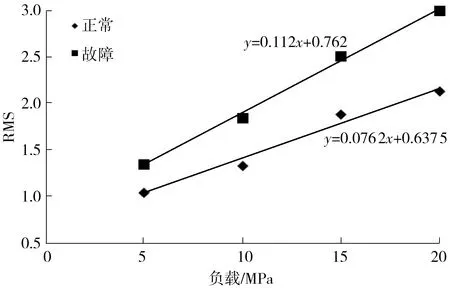
图19 实测轴向振动信号的RMS
从中可以看出,正常情况下趋势线的梯度是0.076 2,松靴故障状态下梯度是0.112。显然,故障状态下的梯度值大于正常状态下的梯度值。
虽然仿真分析中的柱塞泵是7个柱塞,而本次试验中的柱塞泵有9个柱塞,但是从试验中获得的结论与从仿真分析中获得的结论一致,因此本研究提出的变载荷工况下柱塞泵的故障诊断方法是可靠的,适用于各种类型的柱塞泵。
6 结语
本研究构建了柱塞泵的虚拟样机,对柱塞泵不同健康状态、不同负载下的动态响应进行了系统分析,提出了一种变载荷工况柱塞泵松靴故障诊断方法,即首先采集柱塞泵的轴向振动信号并划分成相等的部分,再计算每个分段信号的RMS并计算其趋势线的梯度,然后基于梯度检测柱塞泵的松靴故障。最后通过试验验证了该方法的有效性,得到以下结论:
(1)柱塞泵发生松靴故障时,其振动信号能量会增强,松靴故障越严重,振动信号能量就越大,尤其是轴向振动信号对松靴故障更为敏感。
(2)负载变化对柱塞泵的动态响应有一定影响,这增加了松靴故障诊断的难度。然而,轴向振动的RMS趋势线的梯度能反映松靴故障的敏感特征,可以用来检测松靴故障。

