直驱式波浪发电系统的状态切换控制方法

杨金明 黄伟

(华南理工大学 电力学院，广东 广州 510640)

随着世界经济发展，能源需求逐渐增加，原始的石油资源已不能满足可持续发展的需求。 作为清洁和可再生能源，波浪能受到了广泛的关注和研究。研究表明，全球海岸线附近的可转换波浪能可为人类提供2.5 TW的电力[1]。目前已有多种波浪发电装置，其中直驱式波浪发电装置由于不需要能量转换中间环节而受到广泛的关注[2]。

如何采用功率捕获方法从波浪中捕获最大的功率成为众多学者研究的热点问题。文献[3] 提出一种最优阻尼控制(ODC)方法，该方法通过对不同的波浪周期计算相应的最优阻尼值，并控制直线电磁力与速度使其呈线性关系，从而提高捕获的功率。但由于未使系统达到谐振状态，捕获的功率未能达到最优。文献[4]提出了基于爬山法的最大功率点跟踪(MPPT)控制方法，可通过两个控制变量分别实现对直线发电机的有功功率和无功功率的控制，从而实现波浪激励力和浮子速度同相位。但是该方法的实现是基于波浪在几个小时内变化很小的假设，在不规则波浪下，该方法适用性并未得到验证。文献[5- 6]提出闭锁控制方法，通过加装附加机械装置用浮子钳位来减少波浪激励力和浮子速度之间的相位差，从而尽可能地达到谐振。但是机械装置响应慢，浮子释放时间难以确定。为解决这个问题，文献[7]提出一种有源相位控制(APC)方法，不需要机械装置，根据浮子的加速度和速度信息控制直线发电机使其在保持阻尼系数和最优阻尼系数之间切换，以减少波浪激励力和浮子速度之间的相位差，最终实现MPPT。

本研究以阿基米德浮子式(AWS)波浪发电系统为对象，提出了基于直线发电机的状态切换控制(SSC)方法，对波浪发电装置进行最大功率捕获控制。

1 阿基米德浮子式波浪发电系统

1.1 波浪发电装置模型

图1是AWS波浪发电系统的结构图，永磁直线发电机的定子固定在海底，动子与浮子直接连接，在波浪的作用下，浮子上下往复运动，动子随着浮子上下运动。直线发电机的定子与动子之间产生相对运动，从而将波浪能转化为电能[8]。

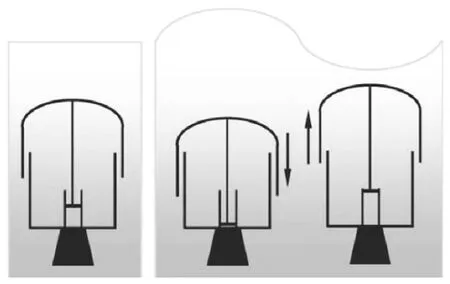
图1 AWS结构

利用流体力学分析和牛顿第二定律，可以得到AWS波浪发电装置的动力学模型[4]:

κhsz(t)+Fg(t)=Fe(t)

(1)

式中:t为时间；Fe为作用在浮子上的波浪激励力；Fg为直线发电机的电磁力；M为浮子的总质量；μ为浮子上的附加质量；Brad为辐射阻尼系数；Bvis为粘滞阻尼系数；κhs为海水的等效弹性系数；z为AWS浮子运动的位移；ω为波浪角频率。波浪激励力幅值Fe、波浪激励力相位φ、附加质量μ(ω)和辐射阻尼系数Brad(ω)可以通过水动力有限元分析软件ANSYS AQWA获得，如图2所示。

1.2 永磁直线发电机模型

采用Park变换，永磁直线发电机在d-q坐标系的电压方程为[9]：

(2)

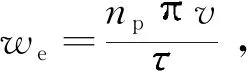
直线发电机的电磁力和电磁功率表示为：

(3)

(4)

1.3 最优阻尼控制方法

状态切换控制方法是在最优阻尼控制方法的基础上实现的，本节对最优阻尼控制方法的原理以及最优阻尼系数进行讨论。文献[3]指出，最优阻尼控制方法中，发电机电磁力和速度成比例关系：

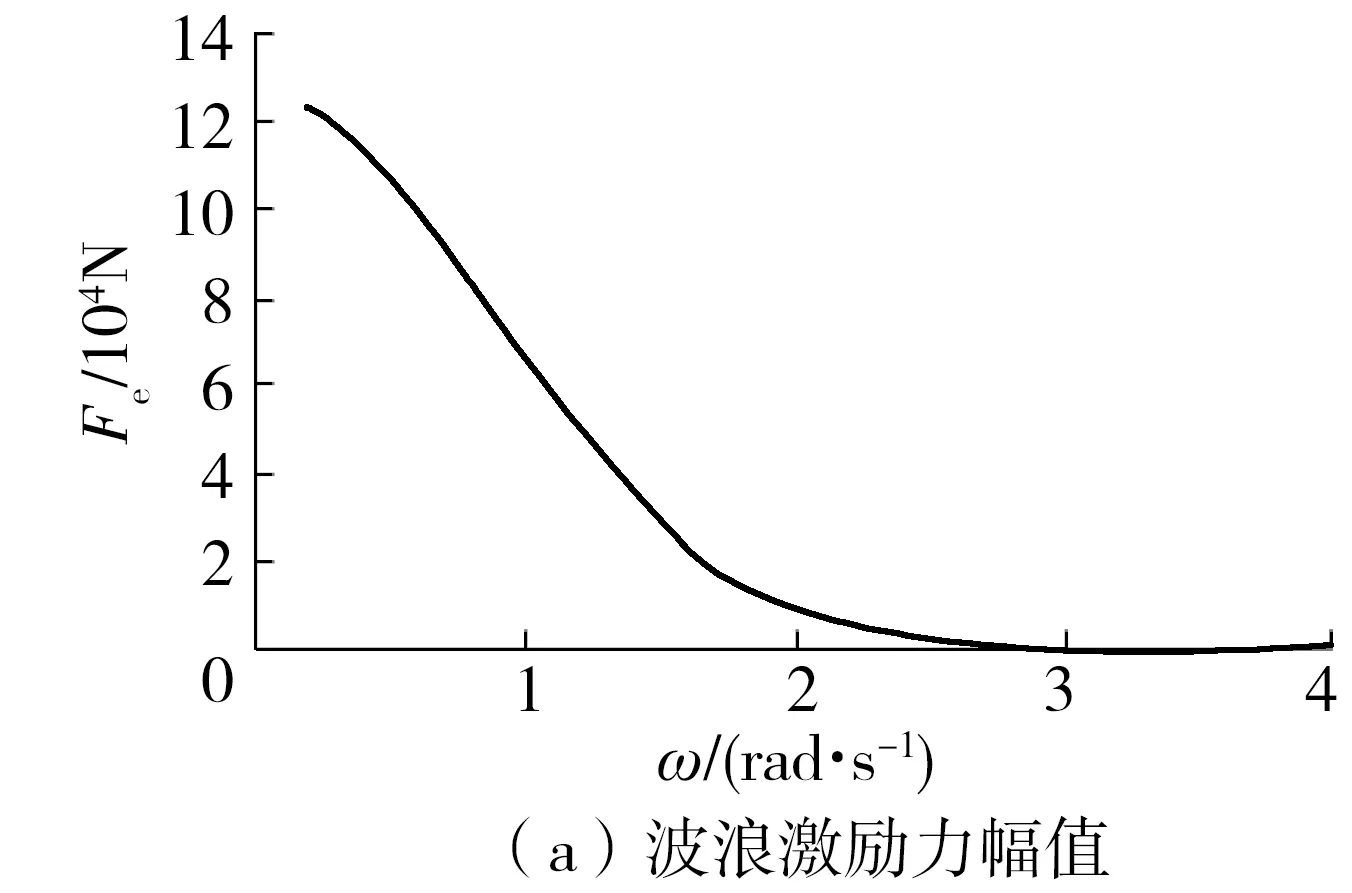
图2 ANSYS AQWA结果

Fg=Bgv

(5)

式中，Bg为直线发电机的阻尼系数，v为直线发电机动子和定子之间的相对速度。平均电磁功率为

(6)

式中，T为波浪周期。最优阻尼系数由式(6)对Bg

求导后可得

(7)

结合式(3)、(5)和(7)，可得最优阻尼控制方法的d、q轴参考电流为：

(8)

(9)

通过控制直线发电机的d、q电流满足式(8)和(9)即可实现ODC方法。

2 状态切换控制方法

2.1 基本原理

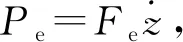
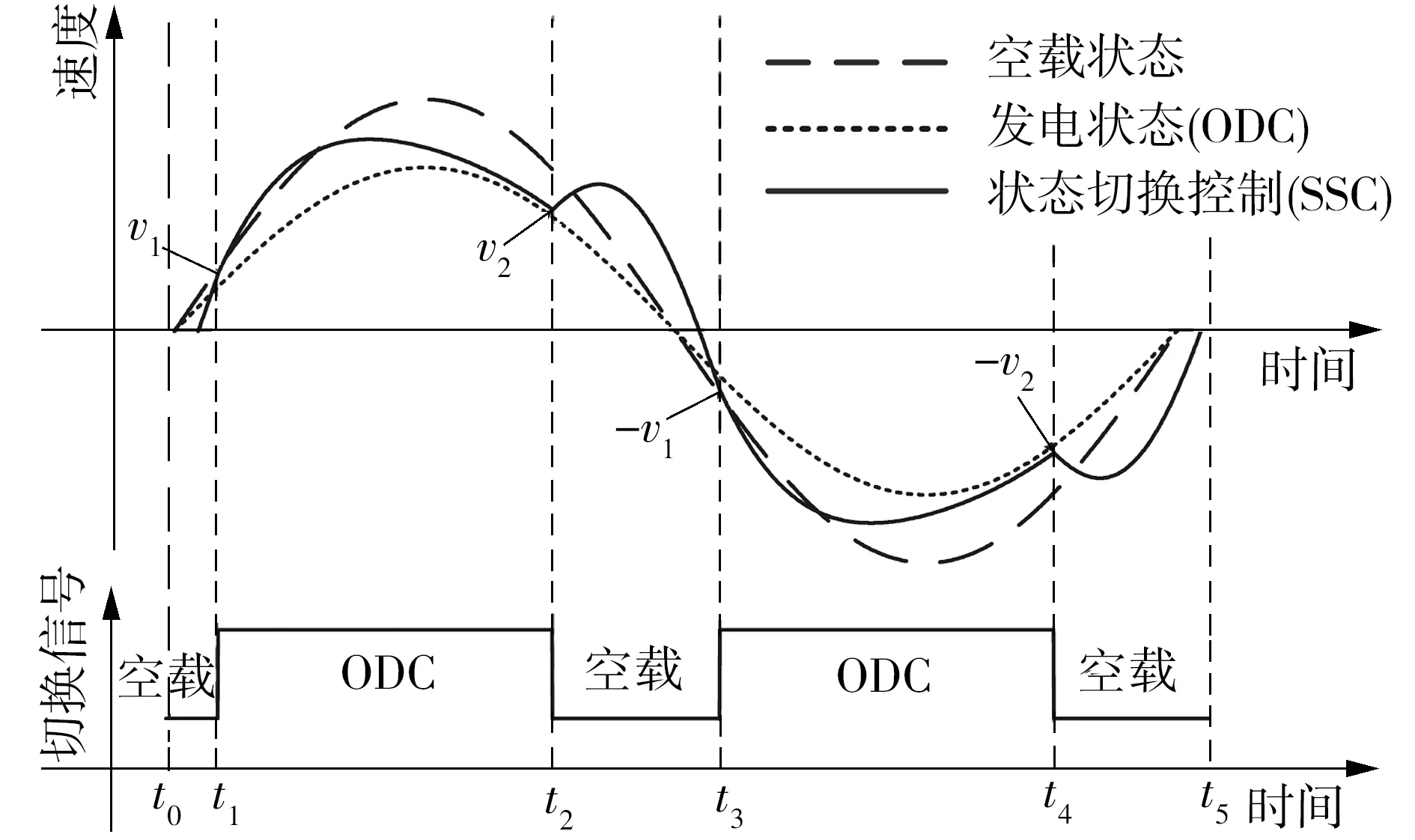
图3 状态切换控制方法原理

2.2 电流命令轨迹规划

(10)

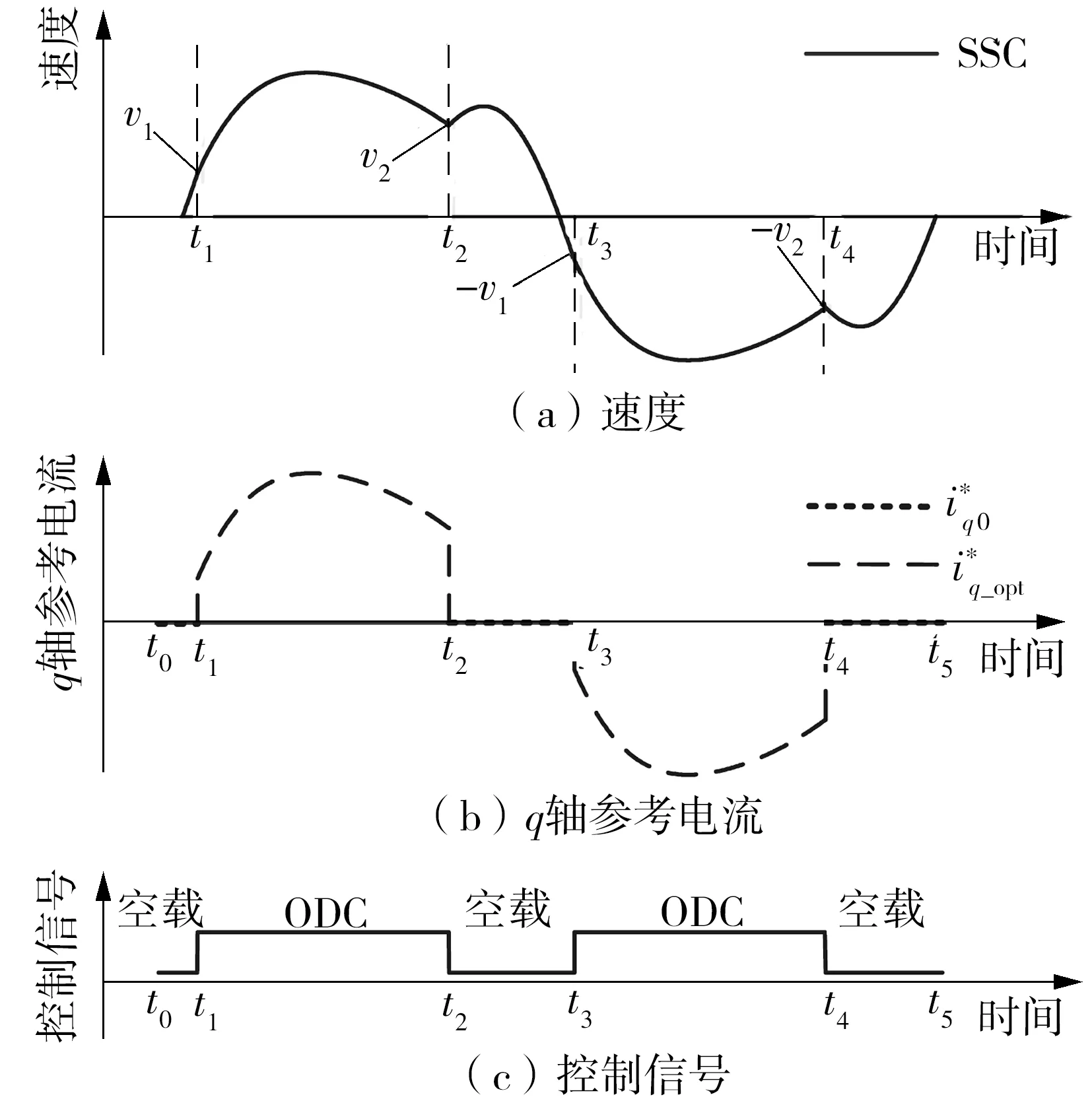
图4 状态切换控制方法实现

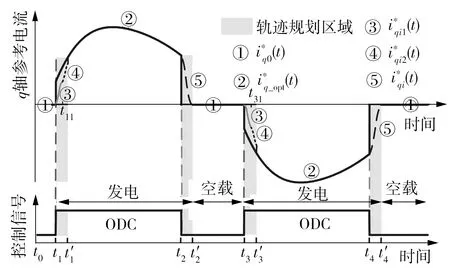
图5 电流命令轨迹规划策略

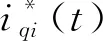
(11)

(12)

式中，t∈[ti,ti1],i=1,3。

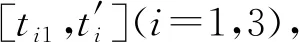
(13)

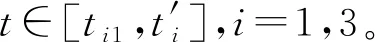
(14)

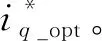
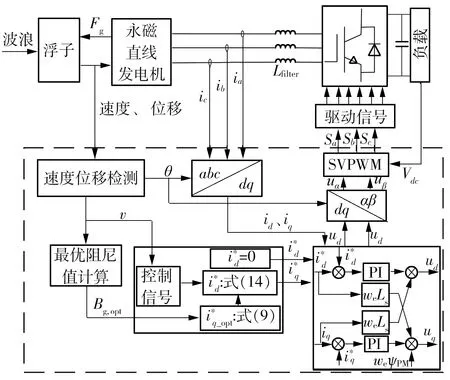
图6 状态切换控制方法框图

3 仿真分析

3.1 仿真参数

在Matlab/Simulink仿真环境中建立阿基米德浮子式波浪发电系统模型，对本研究提出的状态切换控制方法进行验证。波浪发电系统装置参数和直线发电机参数见图2和表1。KP和KI为PI控制器的比例系数和积分系数，使用文献[10- 11]方法进行计算得出。

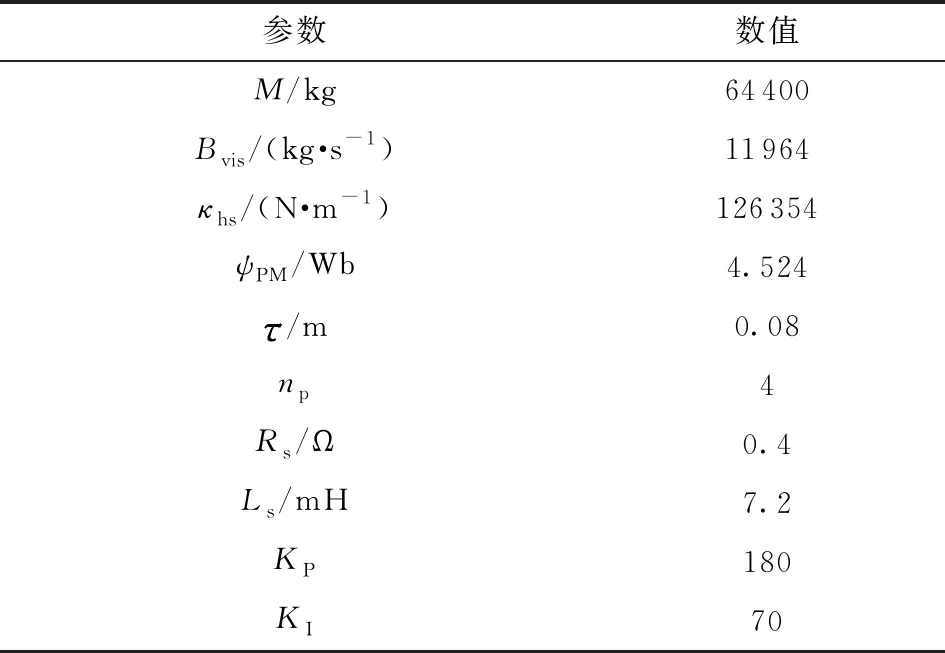
表1 仿真参数

3.2 规则波浪

如图7所示，在周期为5 s的规则波浪作用下，采用状态切换控制方法及其电流命令轨迹规划策略。直线发电机在设定的切入速度v1和切出速度v2切换运行状态，如图7(a)所示，直线电机在速度为v1时切换到发电状态，q轴电流在0.01 s内由0迅速上升到11.71 A;在速度为v2时再次切换到发电状态，q轴电流在0.02 s内由20 A下降到0。通过对q轴电流的控制，实现了发电机在发电状态和空载状态之间的切换。但过大的电流上升率和下降率易造成电机震动，危及主电路中的电力电子器件。如图7(b)所示，采用q轴电流命令轨迹规划策略后，电流由设定好的时间进行变化，从而有效地抑制了能量冲击。同时是在不规则波浪下，采用状态切换控制方法，电流命令轨迹规划策略起着重要作用，这将在不规则波浪仿真中加以分析。切换速度v1=0.3 m/s，v2=0.5 m/s。

图8为周期为5 s的规则波浪作用下，不同切入切出速度下的平均捕获功率。当v1=0 m/s,v2=vopt时,AWS波浪发电系统从波浪中捕获的功率最大。即在速度为0时，控制直线发电机切换到发电状态，存在一个最佳的切出速度vopt。最大功率点相比于切入切出都为0时(即最优阻尼控制方法)的功率增幅为26.29%。

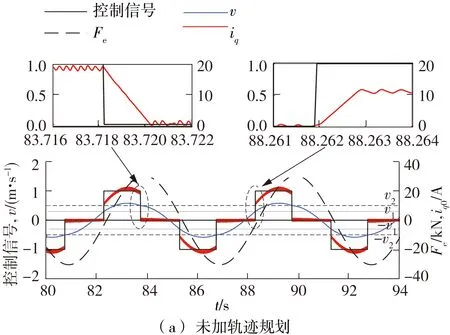
图7 电流命令轨迹规划策略效果

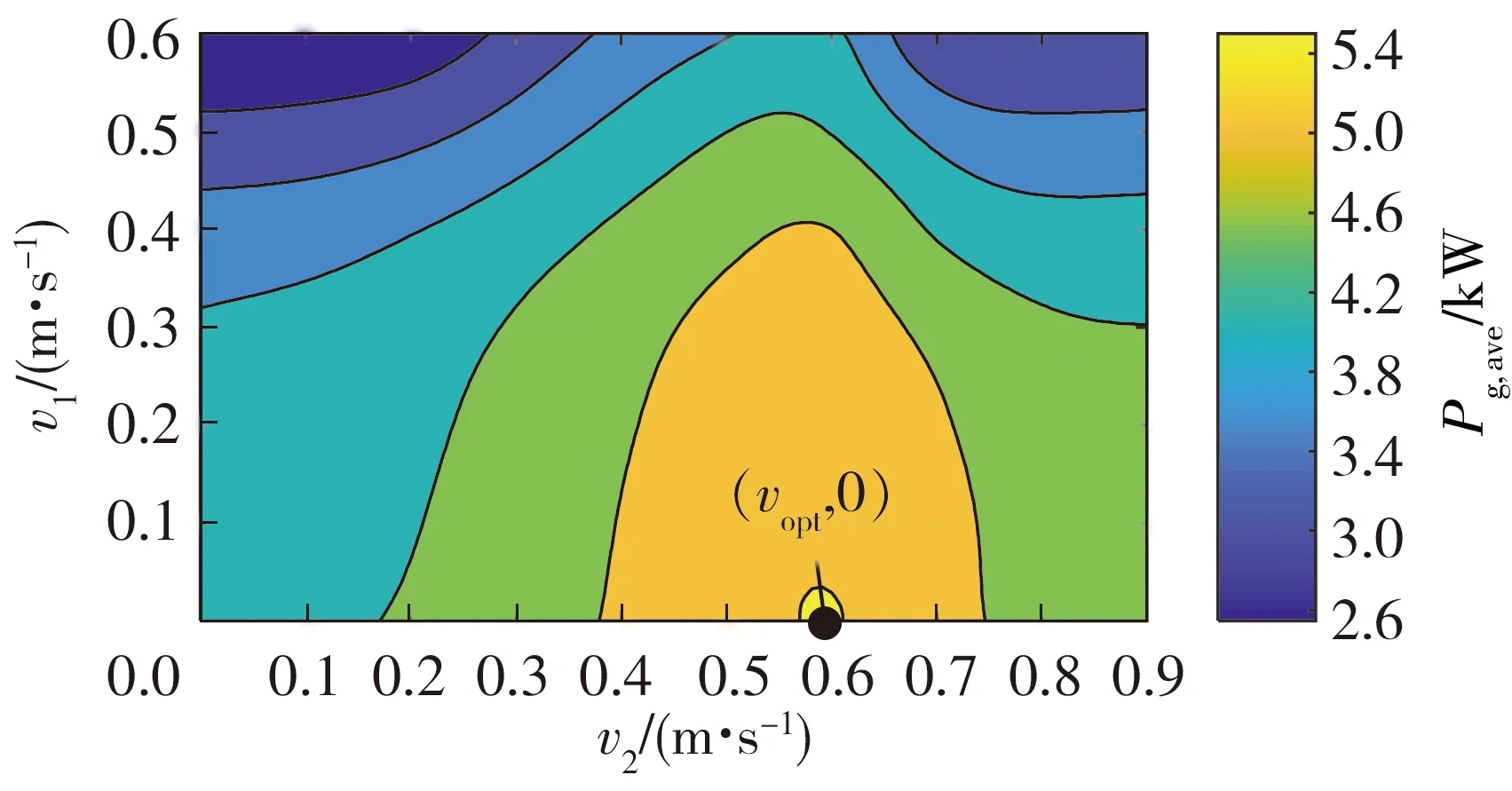
图8 不同切换速度下的平均捕获功率

为了进一步验证状态切换控制方法的性能，与最优阻尼控制(ODC)方法、有源相位控制(APC)方法进行对比。其中，APC方法根据保持区域不同的阻尼值分为APC- 2(保持区域阻尼值2Bg，opt、释放区域阻尼值Bg，opt)、APC- 4(保持区域阻尼值4Bg,opt、释放区域阻尼值Bg,opt)、APC- 6(保持区域阻尼值6Bg,opt、释放区域阻尼值Bg,opt)以及APC-M(保持区域阻尼值Bg,max、释放区域阻尼值Bg，opt),具体分析见文献[7]。如图9所示，在波浪周期小于8 s时，APC-M方法捕获的功率最大，SSC方法在波浪周期大于8 s后捕获的功率最大。但是由于APC方法在保持区域直线发电机阻尼系数是最优值的倍数，将会导致在保持区域直线发电机电流成倍上升，从而增加整个系统的功率损耗；如图10所示，APC方法损耗的功率相比于ODC和SSC都要大。综合考虑捕获功率和功率损耗，SSC方法在4 s到10 s波浪周期范围内均具有很好的性能。

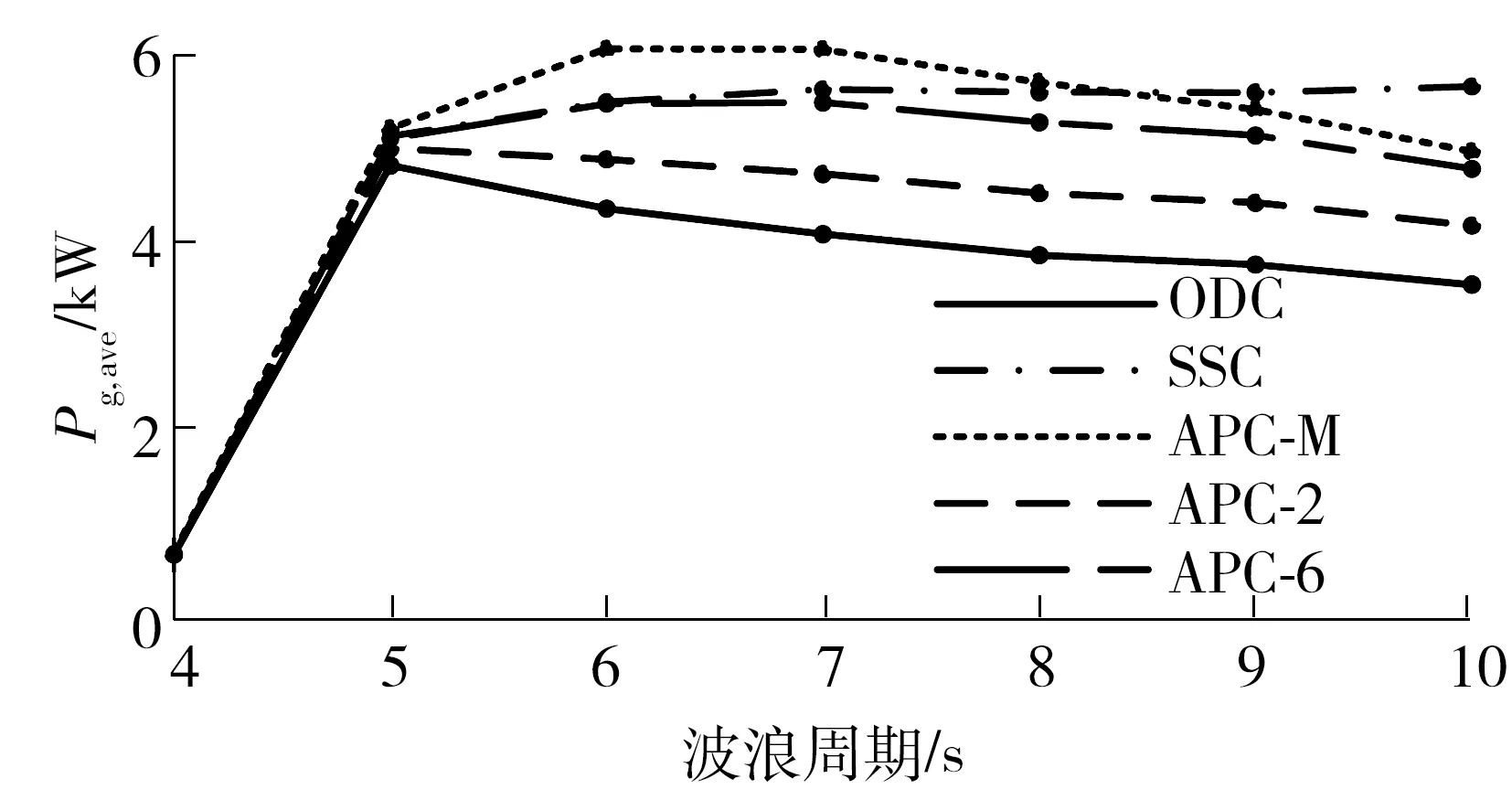
图9 不同方法下的平均捕获功率对比

图10 不同方法下的平均功率损耗对比

3.3 不规则波浪

将海浪视为平稳的随机过程，采用JONSWAP波浪频谱以及Longuet-Higgins波浪模型对不规则波浪进行数值模拟。JONSWAP波浪频谱Sη(ω)的谱型为[12- 13]：

(15)

式中：γ为谱峰升高因子，选择γ为3.3；Hs为有效波高；ωp为波谱的峰值频率；σ为峰形系数。

Longuet-Higgins波浪模型为[14- 15]：

(16)

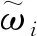
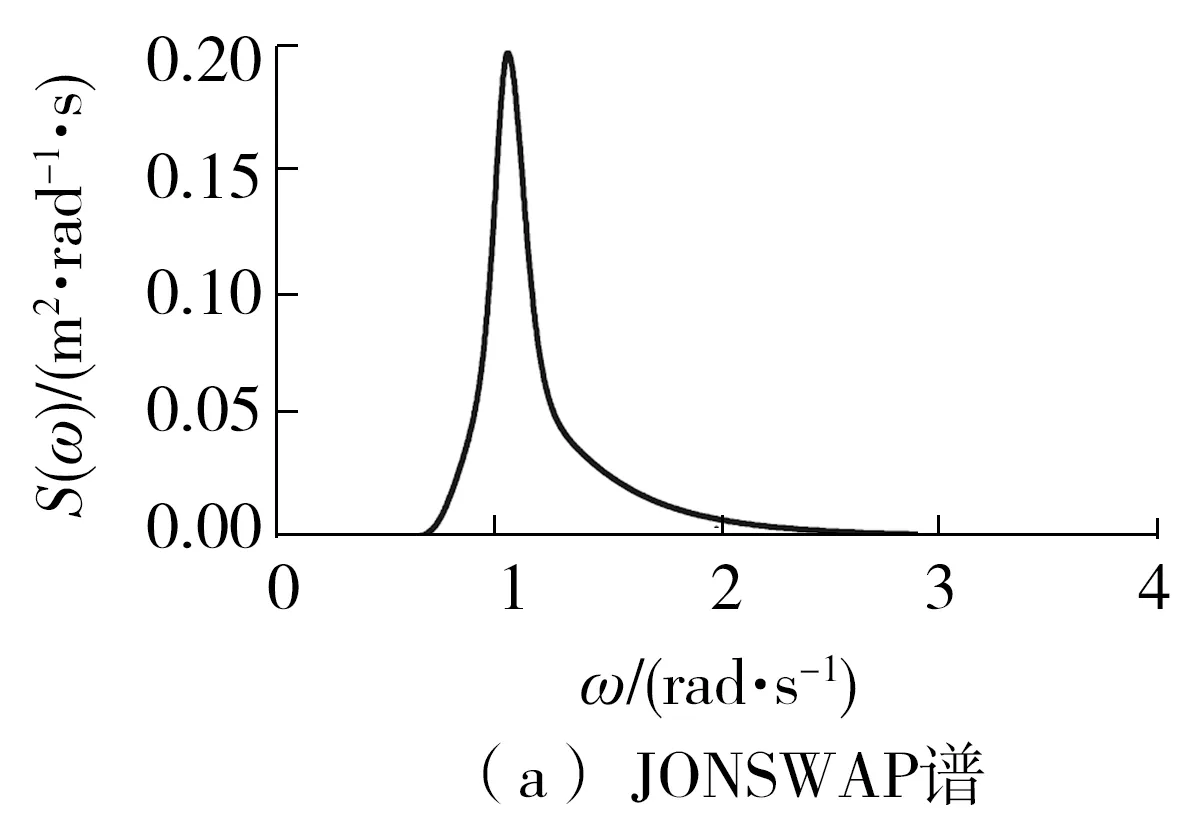
图11 不规则波浪

在规则波浪中存在最优切出速度vopt，为了简化状态切换控制方法在不规则波浪激励下的算法，实时检测速度的峰值，当直线发电机速度到达峰值时，切换到空载状态，电机处于加速状态。如图12所示，对速度进行傅里叶分解，合成速度可被表示成不同频率的速度分量组成。SSC方法算法以合成速度的峰值切出，某些还未到达峰值的速度分量会导致损失部分捕获功率。如图13所示，为减少这部分的损失，设定轨迹规划时间，使q轴电流按设定时间下降到0，直线发电机切换到空载状态。

图14和图15分别示出了不同功率捕获优化方法在不规则波浪条件的捕获功率和功率损耗。当峰值周期Tp为6 s时，APC-M方法捕获的功率最大，SSC和APC- 6捕获性能相近。但SSC方法造成的功率损耗与ODC方法相近，APC-M方法的功率损耗为SSC方法的2.954倍。当峰值周期Tp为8 s时，SSC方法300 s捕获的功率与APC-M相同，但是功率损耗仅为APC-M的0.467倍。综合考虑捕获功率和功率损耗，状态切换控制方法在不规则波浪条件下也表现出优秀的性能。

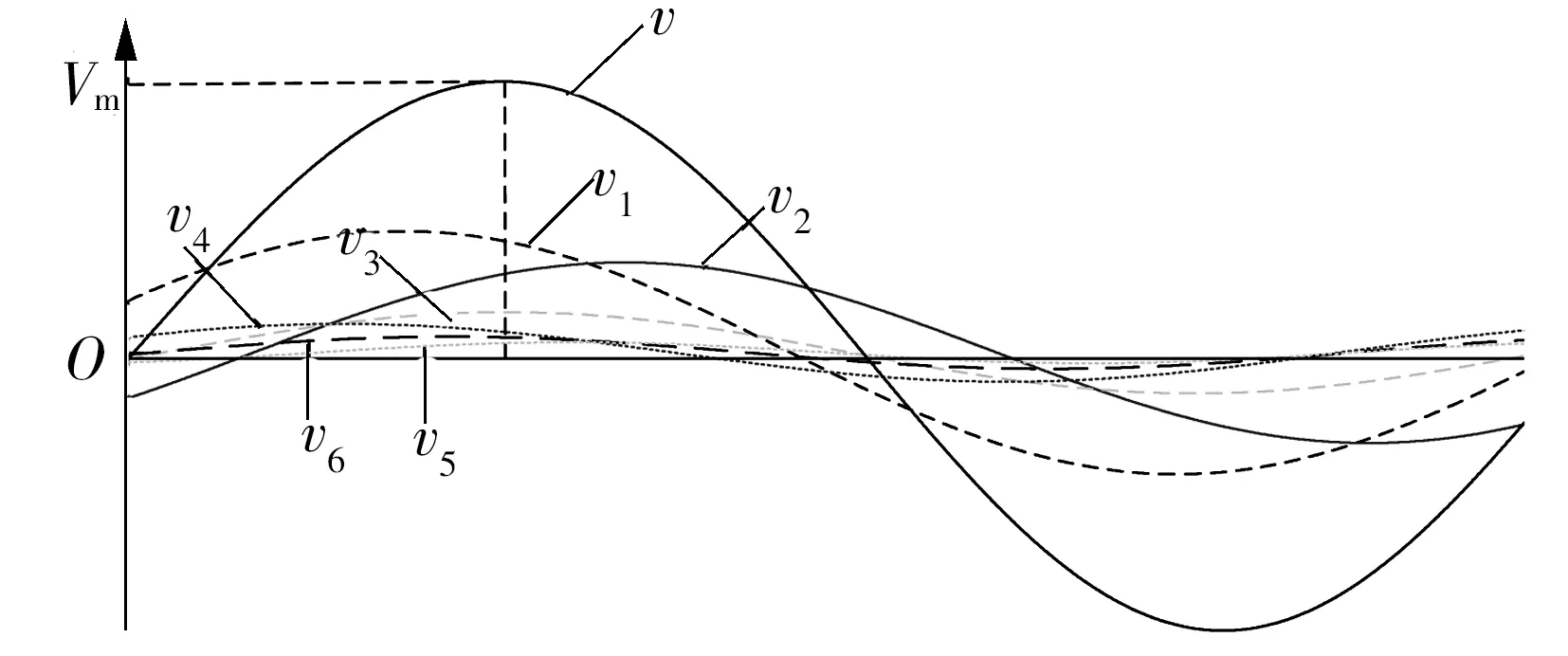
图12 速度频率分解

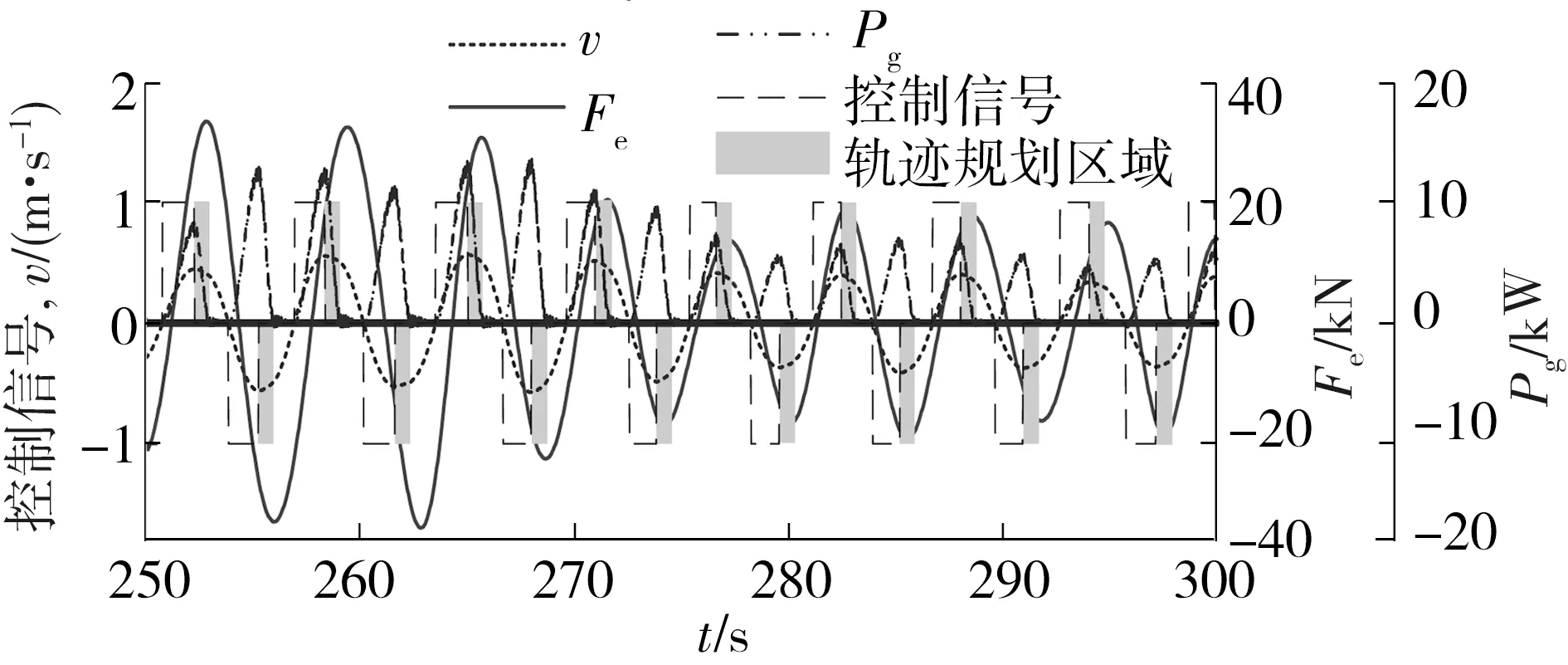
图13 电流命令轨迹规划策略

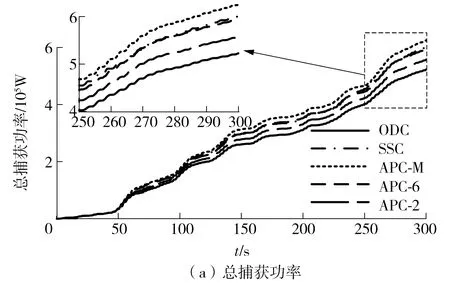
图14 Hs=1 m、Tp=6 s时不同方法下的捕获功率和功率损耗对比

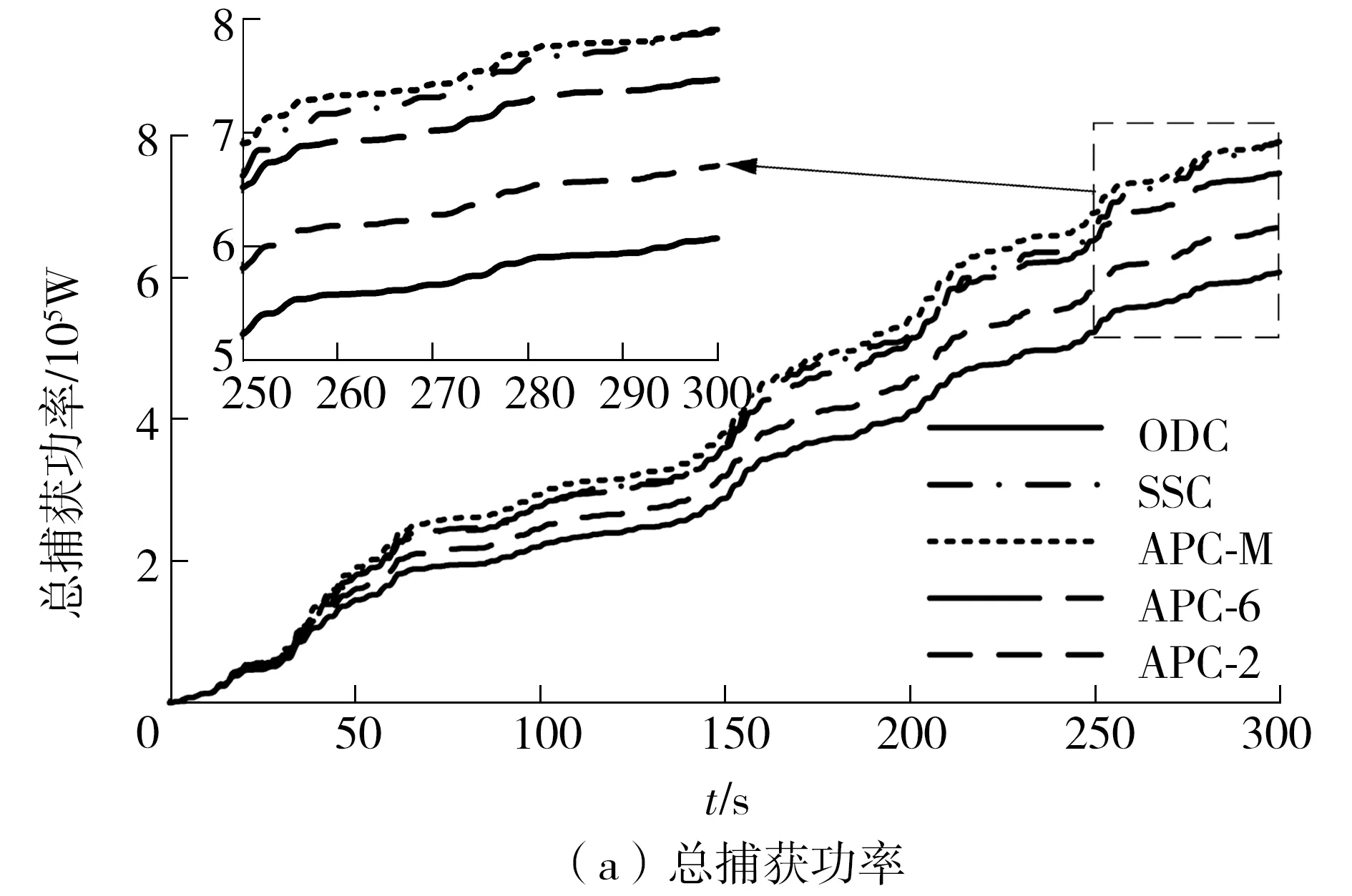
图15 Hs=1 m、Tp=8 s时不同方法下的捕获功率和功率损耗对比

4 结语

通过对直驱式波浪发电系统的功率捕获优化方法研究，提出一种基于直线电机的运行状态切换控制方法及其电流命令轨迹规划方法。在规则波浪和不规则波浪下，对不同功率捕获优化方法进行性能对比。结果显示，本研究提出的状态切换控制方法能够在保证主电路功率损耗较小的同时，使捕获功率相比于其他方法更高。且该方法表现出在波浪的峰值周期越大时性能越优，适用于安装在大峰值周期海域的直驱式波浪发电系统。